The structural–parametric model, the decision of the wave equation, the parametric structural schematic diagram, the transfer functions of the electroelastic actuator of the mechatronics system for the nanotechnology and the ecology research are obtained. Effects of geometric and physical parameters of the piezoactuator and the external load on its dynamic characteristics are determined. The parametric structural schematic diagram and the transfer functions of the piezoactuator for the transverse, longitudinal, shift piezoelectric effects are obtained from the structural–parametric model of the piezoactuator. For calculation of the mechatronics systems for the nanotechnology with the piezoactuator it’s the parametric structural schematic diagram and the transfer functions are determined. The generalized parametric structural schematic diagram of the electroelastic actuator is constructed.

Keywords: electroelastic actuator, piezoactuator, deformation, structural–parametric model, parametric structural schematic diagram, decision wave equations, transfer functions

For the nanotechnology, the ecology research, the nanobiology, the power engineering, the microelectronics, the astronomy for the large compound telescopes, the antennas satellite telescopes and the adaptive optics equipment is promising for use the mechatronics system with the actuator based on the electroelasticity for the piezoelectric or the electrostriction effects. The piezoactuator is the piezomechanical device intended for the actuation of mechanisms, systems or the management based on the piezoelectric effect, the converts electrical signals into the mechanical movement or the force.^1–5 In the present work is solving the problem of building the structural parametric model of the electroelastic actuator in contrast Cady and Mason electrical equivalent circuits for calculation of piezoelectric transmitter and receiver.^6–9 The structural–parametric model of the piezoactuator describes the structure and conversion the energy electric field into the mechanical energy and the corresponding displacements and forces at its the faces. The structural–parametric model of the electroelastic actuator of the mechatronics system is determined by using the method of the mathematical physics. The transfer functions and the parametric structural schematic diagrams of the electroelastic actuator are obtained from its structural–parametric model.^3–14 The piezoactuator for the nano– and microdisplacement of the mechatronics system operates based on the inverse piezoeffect. The displacement is achieved due to deformation of the piezoactuator when the external electric voltage is applied to it. The piezoactuator for the drives of nano– and micrometric movements provide a movement range from several nanometers to tens of micrometers, a sensitivity of up to 10 nm/V, a loading capacity of up to 1000 N, a transmission band of up to 100 Hz. The piezoactuator provides high speed and force, its return to the initial state when switched off. The use of the piezoactuator solves the problems of the precise alignment and the compensation of the temperature and gravitational deformations. The piezoactuator is used in the majority mechatronic systems for the nanotechnology, the ecology research in the scanning tunneling microscopes and the atomic force microscopes.^11–16

The deformation of the electroelastic actuator corresponds to its stressed state. In the piezoactuator there are six stress components $T_1$ , $T_2$ $T_3$ , $T_4$ , $T_5$ , $T_6$  where the components $T_1-T_3$ are related to extension–compression stresses and the components $T_4-T_6$  to shear stresses. The matrix state equations⁸,¹¹ connecting the electric and elastic variables for the polarized piezoceramics have the following form:

$D=dT+{\epsilon }^{T}E$ , (1)

$S=s^{E}T+d^{t}E$ , (2)

where the first equation describes the direct piezoelectric effect, and the second - the inverse piezoelectric effect; $D$  is the column matrix of electric induction along the coordinate axes; $S$  is the column matrix of relative deformations; $T$  is the column matrix of mechanical stresses; $E$  is the column matrix of electric field strength along the coordinate axes; $s^E$  is the elastic compliance matrix for $E=\text{const}$ ; ${\epsilon }^T$  is the matrix of dielectric constants for $T=\text{const}$ ; $d^t$  is the transposed matrix of the piezoelectric modules.

In polarized piezoceramics from lead zirconate titanate PZT for the piezoactuator on Figure 1 there are five independent components $s_{11}^E$ $s_{12}^E$ , $s_{13}^E$ ,$s_{33}^E$ , $s_{11}^E$  in the elastic compliance matrix, three independent components $d_{33}$ ,$d_{31}$ , $d_{15}$  in the transposed matrix of the piezoelectric modules and three independent components, ${\epsilon }_{11}^T$ ,${\epsilon }_{33}^T$ ${\epsilon }_{22}^T$  in the matrix of dielectric constants.

Figure 1 Piezoactuator.

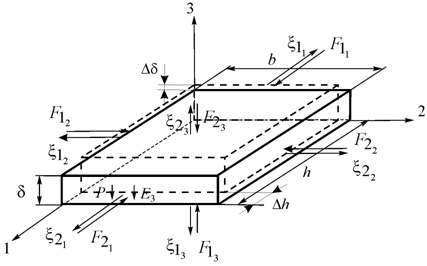
Let us consider the piezoactuator for the longitudinal piezoelectric effect, where $\delta$  is thickness and the electrodes deposited on its faces perpendicular to axis 3, the area of which is equal$S_0$ . The direction of the polarization axis Р, i.e., the direction along which polarization was performed, is usually taken as the direction of axis 3. The equation of the inverse longitudinal piezoelectric effect⁸,¹¹ has the form:

$S_3=d_{33}{E}_3(t)+s_{33}^E{T}_3(x,t)$ , (3)

where $S_3=\partial \xi (x,t)/\partial x$  is the relative displacement of the cross section of the piezoactuator, $d_{33}$  is the piezomodule for the longitudinal piezoeffect, $E_3\left(t\right)=U\left(t\right)/\delta$  is the electric field strength, $U\left(t\right)$ c is the voltage between the electrodes of actuator, $\delta$  is the thickness, $s_{33}^E$  is the elastic compliance along axis 3, and $T_3$  is the mechanical stress along axis 3.

The equation of equilibrium for the force acting on the piezoactuator on Figure 1 can be written as

$T_3{S}_0=F+M\frac{{\partial }^2\xi \left(x,t\right)}{\partial t^2}$ , (4)

Where F is the external force applied to the piezoactuator, $S_0$ is the cross section area and M is the displaced mass.

the equation of the inverse longitudinal piezoeffect, the wave equation using Laplace transform, the equations of the forces acting on the faces of the piezoactuator. The calculations of the piezoactuators are performed using the wave equation⁸,¹¹,¹² describing the wave propagation in the long line with damping but without distortions in the following form:

$\frac{1}{{\left({с}^E\right)}^2}\frac{{\partial }^2\xi \left(x,t\right)}{\partial t^2}+\frac{2\alpha }{c^E}\frac{\partial \xi \left(x,t\right)}{\partial t}+{\alpha }^2\xi \left(x,t\right)=\frac{{\partial }^2\xi \left(x,t\right)}{\partial x^2}$, (5)

where $\xi \left(x,t\right)$  is the displacement of the section, x is the coordinate, t is the time, $c^E$  is the sound speed for $E=\text{const}$, $\alpha$  is the damping coefficient. We can reduce the original problem for the partial differential hyperbolic equation of type (5) using Laplace transform to a simpler problem for the linear ordinary differential equation[10,12]. Applying the Laplace transform to the wave equation (5)

$\Xi \left(x,p\right)=L\left\{\xi \left(x,t\right)\right\}={\displaystyle \underset{0}{\overset{\infty }{\int }}\xi \left(x,t\right)e^{-pt}dt}$, (6)

Setting the zero initial conditions we obtain the linear ordinary second–order differential equation with the parameter p in the form

$\frac{d^2\Xi \left(x,p\right)}{d{x}^2}-{\gamma }^2\Xi \left(x,p\right)=0$, (7)

With its solution being the function

$\Xi \left(x,p\right)=C{e}^{-x\gamma }+B{e}^{x\gamma }$, (8)

Where $\Xi \left(x,p\right)$  is the Laplace transform of the displacement of the section of the piezoelectric actuator, $\gamma =p/c^E+\alpha$  is the propagation coefficient.

We denote for the faces of the piezoactuator

$\Xi \left(0,p\right)={\Xi }_1\left(p\right)$ for $x=0$,(9)

$\Xi (\delta ,p)={\Xi }_2(p)$ for $x=\delta$.

Then we get the coefficients C and B

$C=\left({\Xi }_1{e}^{\delta \gamma }-{\Xi }_2\right)/\left[2\text{sh}\left(\delta \gamma \right)\right]$ ,$B=\left({\Xi }_2-{\Xi }_1{e}^{-\delta \gamma }\right)/\left[2\text{sh}\left(\delta \gamma \right)\right]$ , (10)

The solution (7) can be written as

$\Xi \left(x,p\right)=\left\{{\Xi }_1\left(p\right)\text{sh}\left[\left(\delta -x\right)\gamma \right]+{\Xi }_2\left(p\right)\text{sh}\left(x\gamma \right)\right\}/\text{sh}\left(\delta \gamma \right)$ , (11)

The equations for the forces on the faces of the piezoactuator

$T_3(0,p)S_0=F_1(p)+M_1{p}^2{\Xi }_1(p)$  for $x=0$ , (12)

$T_3\left(\delta ,p\right)S_0=-F_2\left(p\right)-M_2{p}_2{\Xi }_1\left(p\right)$  for $x=\delta$ ,

Where $T_3\left(0,p\right)$  and $T_3\left(\delta ,p\right)$  are determined from the equation of the inverse piezoelectric effect. For $x=0$  and $T_3\left(\delta ,p\right)$ , we obtain the set of equations for determining stresses in the piezoactuator:¹¹⁻¹⁴

$T_3\left(0,p\right)=\frac{1}{s_{33}^E}{\frac{d\Xi \left(x,p\right)}{dx}|}_{x=0}-\frac{d_{33}}{s_{33}^E}{E}_3\left(p\right)$ , (13)

$T_3\left(\delta ,p\right)=\frac{1}{s_{33}^E}{\frac{d\Xi \left(x,p\right)}{dx}|}_{x=\delta }-\frac{d_{33}}{s_{33}^E}{E}_3\left(p\right)$ .

The set of equations (13) yield the set of the equations for the structural–parametric model of the piezoactuator and the parametric structural schematic diagram of the voltage–controlled piezoactuator for the longitudinal piezoelectric effect on Figure 2.

${\Xi }_1\left(p\right)=\left[1/\left(M_1{p}^2\right)\right]\cdot \left\{-F_1\left(p\right)+\left(1/{\chi }_{33}^E\right)\left[d_{33}{E}_3\left(p\right)-\left[\gamma /\text{sh}\left(\delta \gamma \right)\right]\left[\text{ch}\left(\delta \gamma \right){\Xi }_1\left(p\right)-{\Xi }_2\left(p\right)\right]\right]\right\},$  (14)

$\begin{array}{l}{\Xi }_2\left(p\right)=\left[1/\left(M_2{p}^2\right)\right]\cdot \left\{-F_2\left(p\right)+\left(1/{\chi }_{33}^E\right)\left[d_{33}{E}_3\left(p\right)-\left[\gamma /\text{sh}\left(\delta \gamma \right)\right]\left[\text{ch}\left(\delta \gamma \right){\Xi }_2\left(p\right)-{\Xi }_1\left(p\right)\right]\right]\right\},\\ \end{array}$

Where${\chi }_{33}^E=s_{33}^E/S_0$ .

From (2), (3), (14) we obtain the system of the equations describing the generalized structural–parametric model of the electroelastic actuator

${\Xi }_1\left(p\right)=\left[1/\left(M_1{p}^2\right)\right]\cdot \left\{{}^{}-F_1\left(p\right)+{\left(1/{\chi }_{ij}^{\Psi }\right)}_{}^{}\left[d_{mi}{\Psi }_m\left(p\right)-{\left[\gamma /\text{sh}\left(l\gamma \right)\right]}_{}\left[\text{ch}\left(l\gamma \right){\Xi }_1\left(p\right)-{\Xi }_2\left(p\right)\right]\right]\right\},$  (15)

$\begin{array}{l}{\Xi }_2\left(p\right)=\left[1/\left(M_2{p}^2\right)\right]\cdot \left\{{}^{}-F_2\left(p\right)+{\left(1/{\chi }_{ij}^{\Psi }\right)}_{}^{}\left[d_{mi}{\Psi }_m\left(p\right)-{\left[\gamma /\text{sh}\left(l\gamma \right)\right]}_{}\left[\text{ch}\left(l\gamma \right){\Xi }_2\left(p\right)-{\Xi }_1\left(p\right)\right]\right]\right\},\\ \end{array}$

where $d_{mi}=\{\begin{array}{c}{d}_{33},d_{31},d_{15}\\ g_{33},g_{31},g_{15}\end{array}$ , ${\Psi }_m=\{\begin{array}{c}{E}_3,E_3,E_1\\ D_3,D_3,D_1\end{array}$ , $s_{ij}^{\Psi }=\{\begin{array}{c}{s}_{33}^E,s_{11}^E,s_{55}^E\\ s_{33}^D,s_{11}^D,s_{55}^D\end{array}$ , $l=\{\delta ,h,b$ , $c^{\Psi }=\{c^E,c^D$ , ${\gamma }^{\Psi }=\{{\gamma }^E,{\gamma }^D$ ,

${\chi }_{ij}^{\Psi }=s_{ij}^{\Psi }/S_0$ , i = 1, 2…, 6, j = 1, 2, … , 6, m = 1, 2, 3,

Then the parameter $\Psi$  of the control parameter for the electroelastic actuator: E for the voltage control, D for the current control. On Figure 3 is shown the generalized parametric structural schematic diagram of the electroelastic actuator corresponding to the set (15) of the equations.

Figure 2 Parametric structural schematic diagram of a voltage-controlled piezoactuator for longitudinal piezoelectric effect.

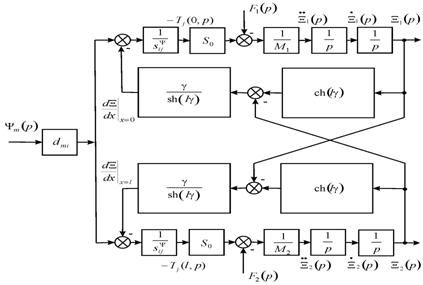
Figure 3 Generalized parametric structural schematic diagram of the electroetoelastic actuator.

From the generalized structural–parametric model (15) of the electroelastic actuator after the algebraic transformations we obtain the transfer functions in matrix form.¹¹⁻¹⁴ The transfer functions are the ratio of the Laplace transform of the displacement of the face for the electroelastic actuator and the Laplace transform of the corresponding control parameter or force at zero initial conditions.

${\Xi }_1(p)=W_{11}\left(p\right){\Psi }_m\left(p\right)+W_{12}\left(p\right)F_1\left(p\right)+W_{13}\left(p\right)F_2\left(p\right)$  , (16)

${\Xi }_2\left(p\right)=W_{21}\left(p\right){\Psi }_m\left(p\right)+W_{22}\left(p\right)F_1\left(p\right)+W_{23}\left(p\right)F_2\left(p\right)$ ,

where the generalized transfer functions

$W_{11}\left(p\right)={\Xi }_1\left(p\right)/{\Psi }_m\left(p\right)={d_{mi}\left[M_2{\chi }_{ij}^{\Psi }{p}^2+\gamma \text{th}\left(l\gamma /2\right)\right]/A}_{ij}{}_{}^{}$ ,

$\begin{array}{l}{A}_{ij}=M_1{M}_2{\left({\chi }_{ij}^{\Psi }\right)}^2{p}^4+\left\{\left(M_1+M_2\right){\chi }_{ij}^{\Psi }/\left[c^{\Psi }\text{th}\left(l\gamma \right)\right]\right\}{p}^3+\left[\left(M_1+M_2\right){\chi }_{ij}^{\Psi }\alpha /\text{th}\left(l\gamma \right)+1/{\left(c^{\Psi }\right)}^2\right]p^2+2\alpha p/c^{\Psi }+{\alpha }^2,\\ \end{array}$

$W_{21}\left(p\right)={\Xi }_2\left(p\right)/{\Psi }_m\left(p\right)={d_{mi}\left[M_1{\chi }_{ij}^{\Psi }{p}^2+\gamma \text{th}\left(l\gamma /2\right)\right]/A}_{ij}{}_{}^{}$ ,

$W_{12}\left(p\right)={\Xi }_1\left(p\right)/F_1\left(p\right)=-{{\chi }_{ij}^{\Psi }{}_{}^{}\left[M_2{\chi }_{ij}^{\Psi }{p}^2+\gamma /\text{th}\left(l\gamma \right)\right]/A}_{ij}$ ,

$W_{13}\left(p\right)={\Xi }_1\left(p\right)/F_2\left(p\right)=W_{22}\left(p\right)={\Xi }_2\left(p\right)/F_1\left(p\right)={\left[{\chi }_{ij}^{\Psi }\gamma /\text{sh}\left(l\gamma \right)\right]/A}_{ij},$

$W_{23}\left(p\right)={\Xi }_2\left(p\right)/F_2\left(p\right)=-{{\chi }_{ij}^{\Psi }\left[M_1{\chi }_{ij}^{\Psi }{p}^2+\gamma /\text{th}\left(l\gamma \right)\right]/A}_{ij}$ .

From the set (15) of the equations we obtain the generalized matrix equation for the electroelastic actuator

$\left(\begin{array}{c}{\Xi }_1\left(p\right)\\ {\Xi }_2\left(p\right)\end{array}\right)=\left(\begin{array}{c}\begin{array}{ccc}{W}_{11}\left(p\right)& W_{12}\left(p\right)& W_{13}\left(p\right)\end{array}\\ \begin{array}{ccc}{W}_{21}\left(p\right)& W_{22}\left(p\right)& W_{23}\left(p\right)\end{array}\end{array}\right)\left(\begin{array}{c}{\Psi }_m\left(p\right)\\ F_1\left(p\right)\\ F_2\left(p\right)\end{array}\right)$ . (17)

Let us find the displacement of the faces for the electroelastic actuator in the stationary regime for the inertial load at ${\Psi }_m\left(t\right)={\Psi }_{m0}\times 1\left(t\right)$ , $F_1\left(t\right)=F_2\left(t\right)=0$ .

Then we get the static displacement of the faces for the electroelastic actuator

$\begin{array}{l}{\xi }_1\left(\infty \right)=\underset{t\to \infty }{\text{lim}}{\xi }_1\left(t\right)=\underset{\begin{array}{c}p\to 0\\ \alpha \to 0\end{array}}{\text{lim}}p{W}_{11}\left(p\right){\Psi }_{m0}/p=d_{mi}l{\Psi }_{m0}\left(M_2+m/2\right)/\left(M_1+M_2+m\right),\\ \end{array}$  (18)

${\xi }_2\left(\infty \right)=\underset{t\to \infty }{\text{lim}}{\xi }_2\left(t\right)=\underset{\begin{array}{c}p\to 0\\ \alpha \to 0\end{array}}{\text{lim}}p{W}_{21}\left(p\right){\Psi }_{m0}/p=d_{mi}l{\Psi }_{m0}\left(M_1+m/2\right)/\left(M_1+M_2+m\right),$  (19)

${\xi }_1\left(\infty \right)+{\xi }_2\left(\infty \right)=\underset{t\to \infty }{\text{lim}}\left({\xi }_1\left(t\right)+{\xi }_2\left(t\right)\right)=d_{mi}l{\Psi }_{m0}$ , (20)

where $m$  is the mass of the electroelastic actuator, $M_1,M_2$  are the load masses.

Let us consider the static characteristics of the piezoactuator from the piezoceramics PZT under the longitudinal piezoelectric effect at $m<<M_1$  and$m<<M_2$ . For $d_{33}=4\cdot {10}^{-10}$ m/V, $U=50$ V, $M_1=2$ kg and $M_2=8$ kg we obtain the static displacement of the faces of the piezoactuator${\xi }_1\left(\infty \right)=16$ nm,${\xi }_2\left(\infty \right)=4$ nm, ${\xi }_1\left(\infty \right)+{\xi }_2\left(\infty \right)=20$ nm. The displacements in the stationary regime of the faces for the piezoactuator under the transverse piezoelectric effect and the inertial load at $U\left(t\right)=U_0\cdot 1\left(t\right)$ ,$E_3\left(t\right)=E_{30}\cdot 1\left(t\right)=\left(U_0/\delta \right)\cdot 1\left(t\right)$ , $F_1\left(t\right)=F_2\left(t\right)=0$  can be written in the following form

$\begin{array}{l}{\xi }_1\left(\infty \right)=\underset{t\to \infty }{\text{lim}}{\xi }_1\left(t\right)=\underset{\begin{array}{c}p\to 0\\ \alpha \to 0\end{array}}{\text{lim}}p{W}_{11}\left(p\right)\left(U_0/\delta \right)/p=d{}_{31}\left(h/\delta \right)U_0\left(M_2+m/2\right)/\left(M_1+M_2+m\right),\\ \end{array}$  (21)

$\begin{array}{l}{\xi }_2\left(\infty \right)=\underset{t\to \infty }{\text{lim}}{\xi }_2\left(t\right)=\underset{\begin{array}{c}p\to 0\\ \alpha \to 0\end{array}}{\text{lim}}p{W}_{21}\left(p\right)\left(U_0/\delta \right)/p=d_{31}\left(h/\delta \right)U_0\left(M_1+m/2\right)/\left(M_1+M_2+m\right)\\ \end{array}$  (22)

${\xi }_1\left(\infty \right)+{\xi }_2\left(\infty \right)=\underset{t\to \infty }{\text{lim}}\left({\xi }_1\left(t\right)+{\xi }_2\left(t\right)\right)=d_{31}\left(h/\delta \right)U_0$ . (23)

From (21), (22) we obtain the static displacements of the faces of the piezoactuator under the transverse piezoeffect at $m<<M_1$ , $m<<M_2$  in the form

${\xi }_1\left(\infty \right)=\underset{t\to \infty }{\text{lim}}{\xi }_1\left(t\right)=\underset{\begin{array}{c}p\to 0\\ \alpha \to 0\end{array}}{\text{lim}}p{W}_{11}\left(p\right)\left(U_0/\delta \right)/p=d_{31}\left(h/\delta \right)U_0{M}_2/\left(M_1+M_2\right),$  (24)

$\begin{array}{l}{\xi }_2\left(\infty \right)=\underset{t\to \infty }{\text{lim}}{\xi }_2\left(t\right)=\underset{\begin{array}{c}p\to 0\\ \alpha \to 0\end{array}}{\text{lim}}p{W}_{21}\left(p\right)\left(U_0/\delta \right)/p=d_{31}\left(h/\delta \right)U_0{M}_1/\left(M_1+M_2\right).\\ \end{array}$  (25)

Let us consider the static characteristics of the piezoactuator from piezoceramics PZT under the transverse piezoelectric effect at$m<<M_1$  and $m<<M_2$ . For $d_{31}=2\cdot {10}^{-10}$ m/V, $h=4\cdot {10}^{-2}$ m, $\delta =2\cdot {10}^{-3}$ m, $U=50$ V, $M_1=2$ kg and $M_2=8$ $M_2=8$ kg we obtain the static displacement of the faces of the piezoelectric actuator ${\xi }_1\left(\infty \right)=160$ nm, ${\xi }_2\left(\infty \right)=40$ nm, ${\xi }_1\left(\infty \right)+{\text{ξ}}_2\left(\infty \right)=200$ nm.

From (16) we obtain the transfer functions of the piezoactuator with the fixed end and the elastic inertial load so that$M_1\to \infty$  and $m<<M_2$  in the following form

$W_2\left(p\right)=\frac{{\Xi }_2\left(p\right)}{U\left(p\right)}=\frac{d_{33}}{\left(1+C_e/C_{33}^E\right){\left(T_t^2{p}^2+2T_t{\xi }_{t}p+1\right)}_{}^{}}$ , (26)

where the time constant $T_t$  and the damping coefficient ${\xi }_t$  are determined by the formulas

$T_t=\sqrt{M_2/\left(C{}_e+C_{33}^E\right)}$ , ${\xi }_t=\alpha {\delta }^2{C}_{33}^E/\left(3c^E\sqrt{M\left(C_e+C_{33}^E\right)}\right)$ .

Let us consider the operation of the piezoactuator from piezoceramics PZT with one face rigidly fixed and the elastic inertial load so that $M_1\to \infty$  and $m<<M_2$  for $M_2=10$ kg,$C_{33}=2.1\cdot {10}^6$  N/m, $C_e=0.4\cdot {10}^6$ N/m we obtain $T_t=2\cdot {10}^{-3}$ c. The experimental and calculated values for the piezoactuator are in agreement to an accuracy of 5%.

The structural–parametric models, the decision of the wave equation, the parametric structural schematic diagram, the transfer functions of the electroelastic actuator are obtained using Laplace transform. The parametric structural schematic diagram and the transfer functions of the piezoactuator for the transverse, longitudinal, shift piezoelectric effects are determined from the structural–parametric model of the electroelastic actuator. The transfer functions in matrix form are describes deformations of the piezoactuator during its operation as part of the mechatronics system for the nanotechnology and the ecology research. From the decision of the electroelasticity equation, the wave equation and the features of the deformations along the coordinate axes we obtain the generalized structural–parametric model and the parametric structural schematic diagram of the electroelastic actuator for the mechatronics system and its dynamic and static properties.

None.

The author declares there is no conflict of interest.

1. Schultz J, Ueda J, Asada H. Cellular Actuators. Oxford: Butterworth– Heinemann Publisher. 2017;382.
2. Uchino K. Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher. 1997;347.
3. Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady mathematics. 2006;73(2):307–313.
4. Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transduser. Doklady physics. 2008;53(3):137–143.
5. Afonin SM. Stability of strain control systems of nano and microdisplacement piezotransducers. Mechanics of solids. 2014;49(2):196–207.
6. Talakokula V, Bhalla S, Ball RJ, et al. Diagnosis of carbonation induced corrosion initiation and progression in reinforced concrete structures using piezo– impedance transducers. Sensors and Actuators A: Physical. 2016;242(1):79–91.
7. Cady WG. Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. New York, London: McGraw– Hill Book Company. 1946;806.
8. Mason W. Physical Acoustics: Principles and Methods. Methods and Devices. New York: Academic Press. 19641(PART A):515.
9. Yang Y, Tang L. Equivalent circuit modeling of piezoelectric energy harvesters. Journal of intelligent material systems and structures. 2009;20(18):2223–2235.
10. Zwillinger D. Handbook of Differential Equations. Boston: Academic Press. 1989;673.
11. Afonin SM. Structural– parametric model and transfer functions of electroelastic actuator for nano and microdisplacement. Chapter 9 in Piezoelectric and Nanomaterials: Fundamentals, Developments and Applications. In: Parinov IA, editor. New York: Nova Science. 2015;225–242.
12. Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady physics. 2005;50(2):77–82.
13. Afonin SM. Parametric structural diagram of a piezoelectric converter. Mechanics of solids. 2002;37(6):85–91.
14. Afonin SM. Block diagrams of a multilayer piezoelectric motor for nano– and microdisplacements based on the transverse piezoeffect. Journal of computer and systems sciences international. 2015;54(3):424–439.
15. Bhushan B. Springer Handbook of Nanotechnology. New York: Springer, 2004;1222.
16. Nalwa HS. Encyclopedia of Nanoscience and Nanotechnology. Calif.: American Scientific Publishers. 2004.