Protection of sea medium with the help of cryogenic engineering is discussed the special problem is considered how to preclude oil leakage at the sea platform digging out raw material on the shelf. Cryogenic engineering may be a great help of freez the water around the injury tube immersed in an aqueous medium. Heat transfer task of ice formation was solved with the help of information approach. Heat transfer under formation of water ice on a flat wall being at low temperature and immersed into aqua media was considered. The heat conductivity of water ice data, obtaind by different authors within a great range et temperature down to cryogenic level were correlated by a hyperbolic expression. The latter gave an opportunity to solve Fourier equation for a layer of water ice forming on a flat wall being at low temperature and immersed in to aqua media the heat transfer task was solved for a constant heat conductivity of ice and with a temperature dependence of it.
Keywords: water ice, heat transfer process, cryogenic temperature, movable border, ınitial and boudering conditions; temperature field, fourier equation, heat conductivity, ıce formation, water media, heat transfer characteristics, specific heat accumulation, ınformation approach
Heat transfer under formation of water ice is a keen process which actual for operation of different types of ice generators, cold accumulators, gasification systems of cryogenics liquid products (LNG, nitrogen, argon) where water media is a source of heat. It is also actual for underwater works, connected with extraction of subjects from the sea shelf as well as liquidation of water oil pollution at the platforms in case if extremely situations arise. Water oil mixture is freeze down into ice slab, which cover the oil leakage location. Such a solid composition is water proved, has a great cohesion if it is kept at a low temperature.
Heat transfer process which is followed by a moving border between water and ice is a quite a hard task for analyses, the math complications is increased if the process is developed under super low temperatures (so called cryogenic level). The problem is concentrated around variability of ice heat transfer characteristics. The most sensitive to temperature is heat conductivity of water ice. Among those who studied temperature dependence of water ice conductivity are.1-4 Most publications on this problem attributed to the temperature range 0÷-100 °C. The information connected with heat conductivity of water ice at lower temperature (cryogenic level and near it) is not wide spread. We may refer to publications of KD Timmerhaus et al.1 Figure 1 suggests experimental data on heat conductivity of water ice at a wide range of temperatures down to cryogenics. As goes from the graph, heat conductivity of water ice is increased with reduction of temperature and at liquid nitrogen level (-196 K) its conductivity is comparative with stainless steel. To describe the heat transfer process with movable water ice border, an analytical correlation between ice conductivity and temperature ought to be known. The analysis of the experimental dater obtaind by different authors and presented on Figure 1 draw us to a conclusion that they may be correlated by KD Timmerhaus1 hyperbolic law.
1
where K=615,34 W/m – dimensional constant, T- temperature of ice K.
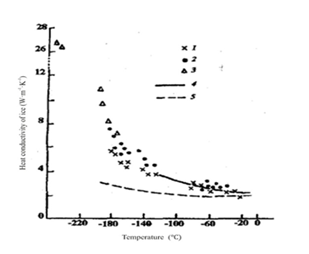
Figure 1 Experimental data of heat conductivity of water ice vs. temperature, obtained by different authors. 1-DS Dillard, KD Timmerhaus, 2–EHRatcliffe, 3–JWDean, KD Timmerhaus, 4–M Jakob, S Erk, 5–CH Lees.
Expression (1) gives quite a good correlation with experimental data of different authors within a great range of temperature including cryogenic level (Figure 2). Later on it will be used for analytic description of heat transfer under formation of ice on the low temperature. Specific heat accumulation of water ice Cp is also depends its temperature but it is less susceptible to it so this dependence can be approximated by a formula
2
Where C=7,970 Dj/(kg·K) – dimensional constant.
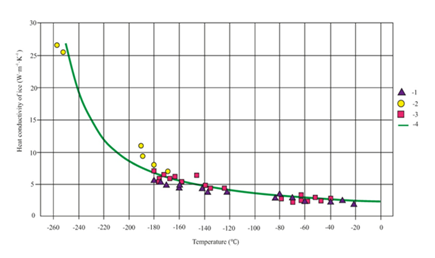
Figure 2 Experimental data on heat conductivity of ice correlated by formula (1).1-DS Dillard, KD Timmerhaus, 2-JW Dean, KD Timmerhaus, 3-E.H.Ratcliffe, 4-formula (1).
Heat transfer process under formation of water ice water ice on the low temperature wall
Fourier unstationary differential equation for a flat wall being at low temperature and immersed into aqua media has the following reduction
3
Temperature field within ice layer can be obtained by solving equation (3) taking into account initial and bordering conditions, which for that case of heat transfer is expresses as
Heat balance on the border ice-water.
4
5
6
7
where λ - heat conductivity of water ice at 0 °C, W/(m·K); α – heat transfer coefficient from the side of water, W/(m2·K); ρice - ice density, kg/m3; L - heat of phase changes (freezing of water into ice), Dj/kg; ξ – thickness of ice layer forming on the flat wall, m; τ - process time, s.
Equation (3) is attributed to unlinear unstationary type with variable transfer coefficients, which can’t be solved in quadratures by a traditional. Methods more fertile results may be obtained on the bases of approximate analytical methods which give result with an acceptable accuracy. An introduction of new variable (information approach5)
8
turning the equation (3) from partial derivation to a full of them.
9
An initial and boundaring conditions take the reduction
10
11
12
where β - is variable factor of ice growth rate
13
14
Suppose the temperature field within the ice layer is expressed as a series
15
Taking in to account expressions (10,11,12,13) the final result of the task is expressed
16
Where T´- fist derivative of T(ν)
17
T´´-is a second derivative of T(ν)
18
Variable factor of growth rate β is found for a accepted time τ by solving (16) if the process is goes on at temperature of the wall Twall > 223 K.
The result is simplificated to
19
The calculations made according equations (16) and (17) revealed that cryogenic temperatures on the wall needs taking into account the temperature dependence of water ice layer (Figure 3).
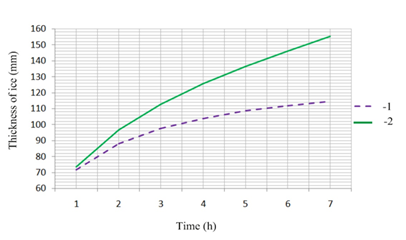
Figure 3 Growth of ice on a flat wall being at cryogenic temperatures and immersed in aqua media (Tw=285 K, α=270 W/(m2·K), Twall=77 K).1 - with constant characteristics of ice, 2-with variable characteristics of ice.




