The Galerkin’s method was used to carry out the elastic instability analysis of biaxially compressed flat rectangular isotropic all-round clamped plates. The biaxial critical buckling load equation was obtained by substituting the plate deflection equation (obtained via the polynomial series) into the Galerkin’s functional. Throughout the analysis, the aspect ratios (defined as the ratio of length, “b” of the plate on the y axis to the length, “a” of plate on the x- axis) was considered to range from 1 to 2. A linear relationship was obtained for the buckling load on the y axis in terms of that on the x-axis. Results for the critical buckling load were obtained for the various aspect ratios (1 to 2) and “k” (relationship constant between forces on the Y- axis and forces on the X-axis) values (0.1 to 1). A maximum buckling load coefficient of 108.0006 was obtained for a square plate at a “k” value of 0, while the least buckling load was 40.50021, obtained for a rectangular plate of aspect ratio equal to 2 and a “k” value of 1.0. At k equal to zero and for all aspect ratios, the results of the present study showed a maximum percentage difference of 0.69389 with those given by Ibearugbulem et al, which shows that the results for the buckling analysis of biaxially loaded CCCC plates presented in this paper for the given aspect ratios and “k” values are very accurate.

Keywords: elastic instability analysis, thin plates, biaxial forces, galerkin’s method, boundary conditions

A, coefficient of deflection of the plate; a, length of the plate; b, width of the plate; W, deflection equation of the plate; H, shape function of the plate; D, flexural rigidity of the plate; $\alpha$ - aspect ratio=b/a; N_x, load applied in the x-direction; N_y, load applied in the y-direction; N_xcr, critical buckling load in the x-direction; h, thickness of the plate; X, primary axis of the plate; Y, secondary axis of the plate; C, clamped support; R, non-dimensional parameter equal to x/a; Q, non-dimensional parameter equal to y/b; F, buckling load coefficient; k, constant, relating ny and nx; Nxi, the critical buckling load coefficients at k=0.i ;$w{\text{'}}^R,w{\text{'}}^Q$ –first derivative of the deflection equation with respect to r and q respectively

Thin rectangular plates are used in the construction of thin walled structures for the transmission of both in-plane and lateral loads. The aeronautic and marine industries make particular use of such materials as thin plates. Thin plates had been defined by Szilard¹ as one whose ratio of its basic dimension to its thickness falls within the range 8…10 ≤ $\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$h$}\right.\le$ 80…100. Due to the importance and wide application of this structural material, several researches had been carried out with the aim of maximizing its potentials for wider structural applications. Areas of research of plate analysis include the vibration of plates, bending of plates and the buckling of plates. Buckling is the phenomenon in which a material under the action of in-plane compressive loads, begins to move from the state of stable equilibrium to a state of unstable equilibrium at a critical value of the compressive loads even when transverse loads are not applied. According to Ventsel & Krauthermmer² failure of thin plate elements may be attributed to an elastic instability and not to the lack of their strength” Therefore, determination of the critical buckling loads of a plate, is essential to safe design of a plate for the intended use of the plate for any Engineering purpose within the safe load. Several works on the buckling analysis of plates had been done in the past. Makhtar et al,³ used a first order shear deformation theory to carry out the thermal buckling analysis of simply supported functionally graded plate and showed that when the plate aspect ratio, $\frac{a}{b}$ is decreased, the critical temperature reduces and the plate becomes thinner. Chajes⁴ showed that the buckling load of a plate simply supported all round and uniformly compressed in one direction is given by Equation 1

$N_x=\frac{D{\pi }^2}{b^2}{\left(\frac{mb}{a}+\frac{n^{2}a}{mb}\right)}^2$

While for a plate fully clamped on all sides and uniaxially loaded, the buckling load is given by Equation 2.

$N_x=\frac{10.67 {\pi }^{2}D}{a^2}$

Singh & Chakrabarti⁵ developed an efficient CoFE model based on higher zigzag theory for the buckling analysis of a uniaxially loaded simply supported cross ply square plate. Jayashankarbabu et al.⁶ used the finite element method to obtain the elastic buckling load factor for square plates of different boundary conditions (such as, SCSC, CCCC, SSSS) containing square and circular cutouts, subjected to uniaxial compression, with the loads applied at the simply supported and at the clamped edges. Yao et al,⁷ proposed a new method which do not require the global stiffness matrix of the system but, reduces the system matrix order and improves the computational efficiency for analyzing plates which are simply supported on all edges. Ezeh et al.⁸ proposed shape functions based on the characteristic orthogonal polynomial and used them in the Galerkin’s indirect variational principle for carrying out the elastic buckling analysis of a thin plate clamped at all edges, and subjected to axial load in the x-direction. Ventsel & Krauthermmer,² Iyengar⁹ & Chajes,⁴ individually, demonstrated that for a biaxially loaded square SSSS plates subject to uniform pressure on both sides, the critical load Ncr, is given by Equation 3.

$N_{cr}=\frac{2 {\pi }^{2}D}{a^2}$  Eqn 3

Ibearugbulem et al.¹⁰ derived a polynomial shape function and used it in the Ritz method to carry out the buckling analysis of plates with boundary conditions (such as the SSSS, CCCC, CSSS, CCSS, CSCS, and the CCCS).From available literature, it will be discovered that works on the buckling analysis of plates had revolved mostly around uniaxially loaded, and square simply supported biaxially loaded plates subject to uniform pressure. To the best of our knowledge, there is extreme dearth of literature on the buckling analysis of all-round clamped thin isotropic square and rectangular plates subject to biaxial loading. The objective of this work, is to fill the gap in literature, by providing solutions to the buckling analysis of all-round clamped thin isotropic rectangular plates subject to biaxial loading (with unequal forces in the both axes) by using the polynomial shape function proposed by Ibearugbulem¹¹ in the Galerkin’s work method to derive the equation for buckling of plates.

The method of solution is detailed as presented in the following stages below.

Formulation of the equation of buckling of biaxially compressed thin rectangular isotropic plates

Consider a fully clamped flat isotropic plate under the action of biaxial compressive in-plane loads as shown in Figure 1. Let the thickness of the plate in the z- direction be far smaller than both the length and width of the plate in the x-and y-directions.

Figure 1 A CCCC Plate Under-going Biaxial Compression.

The overall governing differential equations for plates, is given by Ibearugbulem et al.¹⁰ as, Equation 4

$q-N_x\left(\frac{d^{2}w}{\partial x^2}\right)-2N_{xy}\left(\frac{{\partial }^{2}w}{\partial x\partial y}\right)-N_y\left(\frac{d^{2}w}{\partial y^2}\right)+m{\lambda }^{2}w=D\left[\frac{{\partial }^{4}w}{\partial x^4}+2\frac{{\partial }^{4}w}{\partial x^2\partial y^2}+\frac{{\partial }^{4}w}{\partial y^4}\right]$

Where W = AH     (5)

For biaxial buckling $q=Nxy=m{?}^{2}w=0,$ hence, Ventsel & Krauthammer² gave the buckling equation as; Equation (6)

$-N_x\left(\frac{{\partial }^{2}w}{\partial x^2}\right)-N_y\left(\frac{{\partial }^{2}w}{\partial y^2}\right)=D\left[\frac{{\partial }^{4}w}{\partial x^4}+2\frac{{\partial }^{4}w}{\partial x^2\partial y^2}+\frac{{\partial }^{4}w}{\partial y^4}\right]$

The Equation (6), is the equation of forces acting on the biaxially loaded plate. These forces (both internal and external) acting on the plate, together have the tendency to cause the plate to be deformed. If “w” is the average deformation caused on the plate by the forces, then the work done by the forces on the plates is as given by Equation (7)

$-N_x\left(\frac{{\partial }^{2}w}{\partial x^2}\right)w-N_y\left(\frac{{\partial }^{2}w}{\partial y^2}\right)w=D\left[\frac{{\partial }^{2}w}{\partial x^4}.w+2w.\frac{{\partial }^{4}w}{\partial x^2\partial y^2}+\frac{{\partial }^{4}w}{\partial y^4}.w\right]$

The Equation (7) being Galerkin’s expression for the biaxial buckling of plates at any arbitrary point, was obtained by multiplying Equation (5) by the average deformation “w” of the plate.

The entire work done on the plate, obtained by integrating Equation (7) completely along the x-and y-axes, is given by Equation (8).

$-N_x{{\displaystyle \iint }}^{\text{}}\left(\frac{{\partial }^{2}w}{\partial x^2}\right).w\partial x\partial y-N_y{{\displaystyle \iint }}^{\text{}}\left(\frac{{\partial }^{2}w}{\partial y^2}\right).w\partial x\partial y=D{{\displaystyle \iint }}^{\text{}}\left[\frac{{\partial }^{4}w}{\partial x^4}.w+2w\frac{{\partial }^{4}w}{\partial x^2\partial y^2}+\frac{{\partial }^{4}w}{\partial y^4}.w\right]\partial x\partial y$

 For rapid solution of the plate problem, the Cartesian coordinates, are expressed in terms of non-dimensional parameters as;

$R=\frac{x}{a}andQ=\frac{y}{b}$          (9)

Let the aspect ratio, $\propto$  be given by the Equation (10)

$\propto =\frac{b}{a}$

Substituting Equations (5), (9) and (10) into equation (8), and simplifying gives Equation (11)

$-\frac{N_x}{a^2}{{\displaystyle \iint }}^{\text{}}{\left(\frac{\partial H}{\partial R}\right)}^2\partial R\partial Q-\frac{N_y}{a^2{\propto }^2}{{\displaystyle \iint }}^{\text{}}{\left(\frac{\partial H}{\partial Q}\right)}^2\partial R\partial Q$

$=\frac{D}{a^4}{{\displaystyle \iint }}^{\text{}}\left[\left(\frac{{\partial }^{4}H}{\partial R^4}\right)H+\frac{2H}{{\propto }^2}\left(\frac{{\partial }^{4}H}{\partial R^2\partial Q^2}\right)+\frac{H}{{\propto }^4}\left(\frac{{\partial }^{4}H}{\partial Q^4}\right)\right]\partial R\partial Q$

Let the forces in the x- and y- axes of the plates be related by Equation 12.

$N_y=K{N}_x$

Substituting Equation (12) into (11), and multiplying the resulting equation by a², yields Equation (13)

$-N_x{{\displaystyle \iint }}^{\text{}}{\left(\frac{\partial H}{\partial R}\right)}^2\partial R\partial Q-\frac{K{N}_x}{{\propto }^2}{{\displaystyle \iint }}^{\text{}}{\left(\frac{\partial H}{\partial Q}\right)}^2\partial R\partial Q=\frac{D}{a^2}{{\displaystyle \iint }}^{\text{}}\left[\left(\frac{{\partial }^{4}H}{\partial R^4}\right)H+\frac{2H}{{\propto }^2}\left(\frac{{\partial }^{4}H}{\partial R^2\partial Q^2}\right)+\frac{H}{{\propto }^4}\left(\frac{{\partial }^{4}H}{d{Q}^4}\right)\right]\partial R\partial Q$

Making $N_x$  the subject of the Equation (13), gives the general equation of buckling of a biaxially compressed thin rectangular isotropic plate as Equation (14)

$N_x=-\frac{\raisebox{1ex}{$D$}\!\left/ \!\raisebox{-1ex}{$a^2$}\right.{{\displaystyle \iint }}^{\text{}}\left[\left(\frac{{\partial }^{4}H}{\partial R^4}\right)H+\frac{2H}{{\propto }^2}\left(\frac{{\partial }^{4}H}{\partial R^2\partial Q^2}\right)+\frac{H}{{\propto }^4}\left(\frac{{\partial }^{4}H}{\partial Q^4}\right)\right]\partial R\partial Q}{{{\displaystyle \iint }}^{\text{}}\left[{\left(\frac{\partial H}{{\partial }_R}\right)}^2+\frac{K}{{\propto }^2}{\left(\frac{\partial H}{\partial Q}\right)}^2\right]\partial R\partial Q}$

Taylor-McLaurin’s series formulated deflection function of the CCCC isotropic rectangular plate

Since, for an all-round clamped plate, the deflections and rotations, are zeros at all edges of the plate, the boundary conditions of the SSSS plate is as follows:

$w\left(R=0\right)=w{\text{'}}^R\left(R=0\right)=0$ 15

$w\left(R=1\right)=w{\text{'}}^R\left(R=1\right)=0$  16

$w\left(Q=0\right)=w{\text{'}}^Q\left(Q=0\right)=0$  17

$w\left(Q=1\right)=w{\text{'}}^Q\left(Q=1\right)=0$  18

They ${w^{\prime }}^{R}and{w^{\prime }}^Q$ are the first derivatives of the deflection function, w, in the R-and Q-directions respectively.

Ibearugbulem (2011) assumed the shape function, w, to be continuous and differentiable. He expanded it in Taylor-Mclaurin series and truncated the infinite polynomial series at m = n = 4 and got the general polynomial deflection equation of rectangular plates as follows.

$w={\displaystyle \sum _{m=0}^4{\displaystyle \sum _{n=0}^4{a}_m}}{b}_n{R}^m.Q^n$(19)

Where $a_{m}and\text{}\text{}\text{}\text{}\text{}\text{}{b}_n$  are constants and $RandQ$ are as already defined earlier.

Substituting the first and second boundary conditions (i.e Equations (15) and (16)) into

Equation (19) and solving the resulting simultaneous equations, yields,

$a_0=a_1=0$ , $a_3=-2a_4$  and $a_2=a_4$ .(20)

In the same way, substituting Equations (17) and Equations (18) into Equation (19), yields,

$b_0=b_1=0$ , $b_3=-2b_4$  and $b_2=b_4$ .(21)

Substituting Equations (20) and (21) into Equation (19), gives the particular deflection equation of an all-round clamped isotropic thin rectangular plate as Equation (22)

$w=a_4{b}_4\left(R^2-2R^3+R^4\right)\left(Q^2-2Q^3+Q^4\right)$

Where,

$A=a_4{b}_4$

$H=\left(R^2-2R^3+R^4\right)\left(Q^2-2Q^3+Q^4\right)$

Determination of the critical biaxial buckling loads for CCCC Plates

Differentiating Equation (24) with respect to the R-and Q-axes, gave the following results;

${\left(\frac{\partial H}{\partial R}\right)}^2=\left(4R^2-24R^3+52R^4-48R^5+16R^6\right)*\left(Q^4-4Q^5+6Q^6-4Q^7+Q^8\right)$

$\left(\frac{{\partial }^{4}H}{\partial R^4}\right)H=24\left(Q^2-2Q^3+Q^4\right)$

$\left(\frac{{\partial }^{4}H}{\partial Q^4}\right)H=24\left(R^2-2R^3+R^4\right)$

$\left(\frac{{\partial }^{4}H}{\partial R^2\partial Q^2}\right)H=\left(2R^2-16R^3+38R^4-35R^5+12R^6\right)\left(2Q^2-16Q^3+38Q^4-35Q^5+12Q^6\right)$

Integrating the derivatives of Equations (25) to (2.9) with respect to R and Q from 0-1, yields the results given as Equations (30) to (34):

$\underset{0}{\overset{1}{{\displaystyle \int }}}\underset{0}{\overset{1}{{\displaystyle \int }}}{\left(\begin{array}{c}\partial H\\ \partial R\end{array}\right)}^2\partial R\partial Q=\left[\frac{4}{3}-\frac{24}{4}+\frac{52}{5}-\frac{48}{6}+\frac{16}{7}\right]*\left[\frac{1}{5}-\frac{4}{6}+\frac{6}{7}-\frac{4}{8}+\frac{1}{9}\right]$ $=3.023431587\text{*}{10}^{-5}$

$\underset{0}{\overset{1}{{\displaystyle \int }}}\underset{0}{\overset{1}{{\displaystyle \int }}}{\left(\frac{\partial H}{\partial Q}\right)}^2\partial R\partial Q=\left[\frac{1}{5}-\frac{4}{6}+\frac{6}{7}-\frac{4}{8}+\frac{1}{9}\right]\left[\frac{4}{3}-\frac{24}{4}+\frac{52}{5}-\frac{48}{6}+\frac{16}{7}\right]$ $=3.023431587*?10{?}^{(-5)}$

$\underset{0}{\overset{1}{{\displaystyle \int }}}\underset{0}{\overset{1}{{\displaystyle \int }}}\left(\frac{{\partial }^{4}H}{\partial R^4}\right)H\partial R\partial Q=\left[24\left(\frac{1}{3}-\frac{2}{4}+\frac{1}{5}\right)\left(\frac{1}{5}-\frac{4}{6}+\frac{6}{7}-\frac{4}{8}+\frac{1}{9}\right)\right]$ $=1.269841257*?10{?}^{(-3)}$

$\underset{0}{\overset{1}{{\displaystyle \int }}}\underset{0}{\overset{1}{{\displaystyle \int }}}\left(\frac{{\partial }^{4}H}{\partial Q^4}\right)H\partial R\partial Q=\left[24\left(\frac{1}{5}-\frac{4}{6}+\frac{6}{7}-\frac{4}{8}+\frac{1}{9}\right)\left(\frac{1}{3}-\frac{2}{4}+\frac{1}{5}\right)\right]$ $=1.269841257*?10{?}^{(-3)}$

$\underset{0}{\overset{1}{{\displaystyle \int }}}\underset{0}{\overset{1}{{\displaystyle \int }}}\left(\frac{{\partial }^{4}H}{\partial R^2\partial Q^2}\right)H\partial R\partial Q={\left[\frac{2}{3}-\frac{16}{4}+\frac{38}{5}-\frac{36}{6}+\frac{12}{7}\right]}^2$ = $3.628117911*?10{?}^{(-4)}$

Substituting the numerical values obtained from Equations (30) – (34) into Equation (14), gave

$N_x=-\frac{\frac{D}{a^2}\left[1.26984125\text{*}{10}^{-3}+\frac{2}{{\propto }^2}\left(3.628117911\text{*}{10}^{-4}\right)+\frac{1}{{\propto }^4}\left(1.269841257\text{*}{10}^{-3}\right)\right]}{\left[3.023431587*{10}^{-5}+\frac{k}{{\propto }^2}\left(3.02341587*{10}^{-5}\right)\right]}$

The Equation (35) is the expression for the critical buckling load of a biaxially loaded CCCC plate. While the Equation (36)

$F=-\frac{\left[1.26984125\text{*}{10}^{-3}+\frac{2}{{\propto }^2}\left(3.628117911\text{*}{10}^{-4}\right)+\frac{1}{{\propto }^4}\left(1.269841257\text{*}{10}^{-3}\right)\right]}{\left[3.023431587*{10}^{-5}+\frac{k}{{\propto }^2}\left(3.02341587*{10}^{-5}\right)\right]}$

Is the expression for the biaxial coefficient of an all-round CCCC plate.

The values of the plate aspect ratios (1-2) and the constant “k” varying from 0-1, at intervals of 0.1, were substituted into Equation (36). The results of the critical buckling load coefficients for a biaxially compressed all-round clamped (CCCC) isotropic thin rectangular plate were obtained and presented in Table 1.

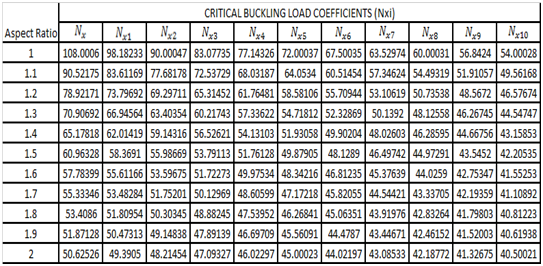
Table 1 Critical Buckling Load Coefficients for biaxially loaded CCCC Plates

Where $N_{xi}\left(i=1,2,3\dots 10\right)$
GaaiilaiaaiodacqGHMacVcaaIXaGaaGimaaGaayjkaiaawMcaaaaa @44B1@ are the critical buckling load coefficients at $k=0.i.$

(where k=Constant, relating Ny and Nxi: and N_xi The Critical buckling load coefficients at various fractions of k )

The results presented in Table 1 were plotted as shown on Figure 2. From Figure 2 and Table 1, it could be observed that, as the aspect ratios increase from one to two, the buckling load coefficients of the CCCC plates reduces. This is because as the aspect ratio increases, the plate begins to behave as a slender column and hence loses its ability to resist load in the y- direction, which causes it to buckle faster; hence, the reduction in the buckling load. It is also observed that as the forces in the y-direction increased (i.e. as “k” increases), the buckling coefficient reduces, this is because as the loads in the y-direction of the plate, increased (with loads applied on the x-axis), the plate becomes weaker and less resistant to applied loads and hence, it buckles faster.

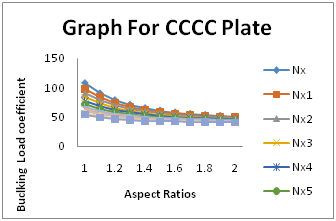
Figure 2 Graph of Critical Buckling Load Coefficients Versus Aspect Ratios of a Biaxially Loaded all round clamped Plate.

The results of the present study were compared with that obtained by Ibearugbulem et al¹² at k=0 (uniaxial buckling only, of CCCC plates) as presented on Table 2. From the Table 2, it is seen that, the results of this present work agrees very closely with established results of uniaxially loaded CCCC plates subject to uniform pressure along the x-axis. (i.e. at k = 0), for different aspect ratios. This therefore, validates the results of the critical buckling load coefficients for the other k values (presented on Table 1) for which there are no existing results in literature.

From the study, the following conclusions have been, drawn: The equation for the determination of the critical buckling loads for a biaxially loaded all- round clamped thin rectangular isotropic plate, for all aspect ratios and k-values, has been derived in this work. The critical buckling load coefficients for a biaxially loaded thin rectangular isotropic plates, have been determined for different aspect ratios and k-values. Given that the results obtained from this work agrees with the results of Ibearugbulem¹¹ at k = 0, it therefore follows that, the results obtained in this work for other k values (for which there are no other existing results to compare with, in literature), are also correct.

The polynomial shape function used in this work (based on the Tailor-Mclaurin series) can be said to have accurately defined the plate’s deformed shape, given the high accuracy of the buckling load coefficients obtained. Given the difficulty in the use of the trigonometric shape functions to determine the critical buckling load coefficients of an all-round clamped thin rectangular isotropic plate, the use of the equations and tables developed in this work is recommended for a quick and easy analysis of the buckling loads of such plates, for other aspect ratios which are not covered in this work.

None.

The author declares no conflict of interest.

1. Rudolph Szilard. Theories and applications of plates analysis. Classical, Numerical and Engineering Method. USA: John wiley and sons Inc; 2004. 1056 p.
2. Ventsel E, Krauthermmer T. Thin Plates and Shells. Theory, Analysis and Applications. New York: Marcel Dekker; 2001.
3. Bouazza M, Younsi A, Adda Bedia El Abbas, et al. Buckling Analysis of Functionally Graded Plates With simply Supported Edges. Leonardo Journal of sciences. 2009;15:21–32.
4. Chajes Alexander. Principles of Structural Stability Theory. USA: Previse–Hall Inc Englewood Cliffs; 1974. p. 238–297.
5. Singh SK, Chakrabarti A. Buckling Analysis of Laminated Composite Plates Using an Efficient C0 FE Model. Latin American Journal of Solids and Structures. 2012:9(3).
6. Jayashankarbabu BS, Karisiddappa. Stability Analysis of Thick Plates with eccentric Cutout. International Journal of Engineering Technology and Advanced Engineering. 2013:3(8).
7. Li–ke, Yao, Biritle, et al. Semi Analytical Finite Strip Transfer Matrix Method for Buckling Analysis of Rectangular Thin Plates. Journal of mathematical Problems in Engineering. 2015;2015:11.
8. Ezeh JC, Ibearugbulem OM, Opara HE, et al. Galerkin’s indirect Variational Method in Elastic stability Analysis of All Edges Clamped Thin Rectangular Flat Plates. International Journal of Research in Engineering and Technology. 2014:3(4)
9. Iyengar. Structural Stability of Columns and plates. 1st ed. England: Ellis Horwood Limited; 1988. p. 138–179.
10. Ibearugbulem OM, Ezeh JC, Ettu LO. Energy Methods in Theory of Rectangular Plates (Use of Polynomial Shape Functions). Nigeria: Liu House of Excellence Venture; 2014.
11. Ibearugulem OM. Application of a Direct Variational Principle in Elastic Stability of Rectangular Flat Thin Plates. Nigeria: Ph.D. Thesis submitted to the Postgraduate School, Federal University of Technology Owerri; 2011.
12. Iwuoha SE. Buckling Analysis of Plates subjected to Biaxial Forces Using the Galerkin’s Method. Nigeria: MENG Thesis submitted to the Post graduate School, Federal University of Technology Owerri; 2016. 2(2).