Recent studies in neurosciences have produced evidence suggesting that Glial cells play a vital role in assisting neurons to form synaptic connections, contrary to a previously held view that they played a less significant role in the synaptic function. The neurochemical processes underlying the transmission is observed to be both temperature dependent, and ionic conduction, enabling faster communication. These results have opened up a few key questions: what role do Glia play in information processing, learning, memory, and retention in the brain? This opens up the possibility for on-demand interconnection for low-latency synaptic connection between otherwise unconnected nodes, and their importance to scale the performance of very large neural networks, typically trained by deep learning, but designed to act on inputs originating from very large geo-distributed areas. In this paper, we propose a new framework for Unsupervised Deep Learning (UDL) that takes into account the existence of such interconnections. The theory is based on the thermodynamic equilibrium of human brains that are kept at a constant temperature to make effortless decisions of all incoming sensory data at the Helmholtz Minimum Free Energy (MFE). This is referred to as a Natural Intelligence (NI) as opposed to AI in the sense of a non-contrived straightforward decision. Likewise, the trustworthiness of MFE classifier will be comprehensible with Human Visual System (HVS) with sparse Ortho-Normal (ON) Salient Feature Extraction (SFE). The MFE cost function is derived from first principles obtained from nature: one, the Homeostasis principle; and two, real-time duplicative sensory inputs. The Homeostasis condition maintains constant brain temperature, which implies constant biochemistry reaction rates resulting in the same learning experience among all generations of Homosapiens. The Power of Paired sensory inputs from eyes, ears, nostrils, tessellate tasting buds, tactile touching sensing has real-time pre-processing that exploits the agreement is the signal, while the disagreements are the noises, and the input signal energy relaxes to the averaged brain temperature as the UDL. A mathematical definition of Glial (Greek: glue) cells seems to corroborate with modern neuroscience of living animals.

There are tens of billions of Neurons and hundreds of billions of Glial cells that keep our brains operating smoothly. Any imbalance between two can generate disorders. Thus the crossover Rosette Stone between ANN Back Propagation delta vs. glial and dendrites vs nets as well as BNN UDL ANN SDL. These cross-over will be facilitated for medical image screening and tracking. While a living system might be sick by either DNA genome or epigenetic phoneme, the machine can likewise crash by programming bugs. For example, when the glial force be too strong divergent, implicating the Glioma tumors, when Astrocytes glial servant cells go on strike: slow down (lacking of deep sleep) leading to Alzheimers. We believe the artificial machine can compute the cause and the effect helping radiologists' screenings and diagnoses. The experimental characterization of those electrical insulated white matter made of six types of Glial cells in live animals might help proactively & early diagnose by means of powerful machine learning, and thus improve treatment of the disorders of human nervous system.

Keywords: deep learning, neurons, ANN, AI, supervised deep learning, BNN, NI, unsupervised deep learning, glial cells

We leverage and generalize the recent success of AI Supervised Deep Learning (SDL) by Internet IndustrialConsortium to Natural Intelligence (NI) Unsupervised Deep Learning(UDL).Since Learning is merely seeking Gradients Descent (GD), then the abstract mathematics of"digging a hole," supervised or not, is merely to determine where to dig. The Algorithm of “hole digging” is formally isomorphic. The only difference between two is the cost function whichfor SDL is the Least Mena Square (LMS) between actual output and desired output; for UDL turns out to be keep those co-incident account agreed signals of two eyes, two ears, and reject those disagreed noise by relaxing toward the brain thermal reservoir at a constant brain temperature 37oC thermodynamic Minimum Free Energy (MFE). This thermodynamic equilibrium requires no supervision the decision is effortless Natural Intelligence at MFE. The cross over isomorphic between the language of physics to natural processing suggests to the reader an analogy with the computational AI approach. This should lead a breakthrough which allows early diagnosis & track brain disorders related to glioma.

Webster’s Dictionary (New Riverside University) defines bionics as: “application of biological principles to the design and studies of engineering systems, esp. electronics systems.” What are the essential biological principles that can be emulated? It may be the crossover between Natural Intelligent (NI) behaviors and theArtificial Intelligence (AI) that will be beneficial to Automatic Target Recognition (ATR), natural languagerecognition, hand-written OCR, etc. Big & fast Machines, e.g. EXXACT by Nvidiaat the tune of millions dollars, can handle billions of labeled images, e.g. Google Cloud images. Those democratized billions of examples in the Cloud can be crunched through machines thousands to millions of nodes, and over tenth to hundredth layers. As a result of Big Data Analyses (BDA), the error rate has been significantly reduced from a quarter to few digits.

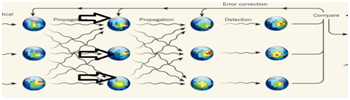
We leverage the recent success of BDA by Internet Industrial Consortium. For example, Google co-founder Sergey Brin sponsored AI AlphaGo was surprised by the intuition, the beauty & the communication skills displayed by AlphaGo. As a matter of fact, Google Brain Alpha Goavatar beat Korea grandmaster Lee SeDol in Chinese Go Game 4:1 as millions watched in real time Sunday March 13, 2016 on the World Wide Web. This accomplishment has surprised and surpassed WWII Alan Turing definition of AI that cannot tell the other end whether is human or machine. Now six decades later, the other end can beat a human. Likewise, Facebook has trained 3-D color blocks image recognition, will eventually provide an age & emotional-independent faces recognition up to 97%. YouTube will produce Cliff Note automatically about all the Video in YouTube and discovered by Andrew Ng at Baidu out of surprise the favorite pet of mankind to be Cat, not dog! As such DARPA Information Innovation Office Mr. David Gunning demanded the reason for why machine decision to be cat. Otherwise, DOD could not trust the machine decision in order to execute adversary action. DARPA began 5 years program 2016-2021 to develop explainable AI (XAI). Such speech pattern recognition capability of BDA by Baidu has utilized the massively parallel & distributed computing based on the classical Artificial Neural Networks (ANN) with Supervised Deep Learning (SDL) called Deep Speech outperform HMMs. We examine deeper into the deep learning technologies, which are more than just software’s: ANN & SDL, because the software’s have been with us over three decades, since 1988 developed concurrently by Paul Werbos (“Beyond Regression: New Tools for Prediction and Analyses” Ph.D. Harvard Univ.1974), McCelland, & Rumelhart (PDP, MIT Press, 1986). Notably, the key is due to the persistent visionaries: Geoffrey Hinton & his protégées: Andrew Ng, Yann LeCun, Yoshua Bengio, George Dahl, et al.(cf. “Deep Learning,” Nature, 2015), who have participated major IT as chief scientists and chief technologist & engineers to program on Massively Parallel & Distributed (MPD) Supercomputer e.g. Graphic Processor Units (GPU). A GPU has eight CPUs per Rack & 8x8=64 Racks per noisy air-cooled room size at the total cost of millions of dollars. Thus, toward UDL, we program on mini-supercomputers and then program on the GPU hardware and change the ANN software SDL to BNN “Wetware,” since the brain is a 3-D Carbon-computing, rather 2-D Silicon computing, it involves more than 70% water substance.

The ubiquitous machine performance cost function is a type of a nearest neighbor classifier by means of Least Mean Square (LMS) errors at minimum ${\Vert Cause-effect\Vert }^2$ , between the desired (cause interpretation) and the actual (effect behavior); the latter may be referred to as SDL algorithms. Our model might be summarized for layman as if "it takes two to Tango in the constant temperature brain (Homeostasis) unsupervised deep learning." The derivation of deep learning back-prop algorithm for both biological Unsupervised Deep Learning (UDL) & classical SDL are given. While the cost function of UDL will be proved to be Helmholtz Minimum Free Energy (MFE), the cost function of SDL is Least Mean Square (LMS) Errors between desired output and actual input. The pseudo code is identical in both cost functions.

The difference is the interpretation of error gradients. While the negative MFE gradient defines${\stackrel{\rightharpoonup }{g}}_j\equiv -\frac{\Delta MFE}{\Delta dendrit{e}_j}$ $dendrit{e}_j\equiv \left[W_{j,\alpha }\right]S_{\alpha }$ of biological Neuroglia cells${\stackrel{\rightharpoonup }{g}}_j$ ; the negative LMS gradient defines the classical delta ${\stackrel{\rightharpoonup }{\delta }}_j\equiv -\frac{\Delta LMS}{\Delta ne{t}_j}$ >$ne{t}_j\equiv \left[W_{j,\beta }\right]o_{\beta }$ For the convenience in bookkeeping, Einstein tensor index conversion is adopted that a repeated Greek indices:$\alpha ,\beta ,\gamma$ are summing over the integers of Latin index: i, j, k.

ANN applied to law enforcement surveillance

For example, we know from experience a perpetrator always surveys a new site, say mobile missile launcher Patriot, so that he or she can come at the night to defuse the missile and damage the launcher. We consider such a persistent surveillance (7 days -24 hours) application at the Access Control Environment (ACE) critical perimeter, known as “Cross Modality Pattern Recognition (CMPR)” CMPR is useful with a set of passive day and night cameras at the perimeter. The million dollar question is that for man-in-the-loop how to associate day pictures with night pictures.

We can pair off the set of multiple spectral pictures e.g. from Google Cloud Storage Image Data bases, Figure 1. We can have side-by-side the daytime grey scale pictures, one pixel per one node as a vector daytime images$X_j\left(\stackrel{\rightharpoonup }{x},t\right)$ . The set of day and multiple spectral IR images are denoted as the desirable pictures $Y_k\left(\stackrel{\rightharpoonup }{x},t\right)$ made of infrared multiple spectral images denoted as “Z Wave Infrared (ZWIR)” where Z stands for {Short(0.8-1$\mu$ ), Middle (3~5$\mu$ ), Long (8~12$\mu$ )} due to the atmospheric propagation window. ANN may be thought of as unbiased review committee. Each layer of committee members called nodes can scrutinize specific features to give their individual opinions. Then they pass their decision to the next layer of committee, and so on and so forth. These committee members like ANN may be mathematically characterized as the following four necessary conditions:

1. Each member node has an individual degree of freedom (d. o. f.) in terms of a logistic threshold logic $0\le S_k\equiv {\sigma }_k\left(ne{t}_k\right)\le 1\left(\sim 100Hz\right)$ and where input $ne{t}_k={\sum }_i\left[W_{k,i}\right]S_i$
2. Initiate the matrix,$\left|\left[W_{k,i}\right]\right|<1$ i.i.d..

3.  $\left[W_{j,k}\right]\propto {\delta }_j{S}_k$ “Wired together, fired together.” D.O. Hebb
4.  ${\delta }_j=-\frac{\text{Δ}LMS}{\text{Δ}ne{t}_j}$ ; error force derived from error energy slope w.r.t. all input nodes decision firing rates

ANN training procedure

Given a set of day image $\left\{X_j\left(x,t\right)\right\}$ that each image has say 50x50 of 6 bits gray value $\left(1<X<128\right)$  we feed each image pixels one-to-one to each nodes of input layer of ANN, then each node broadcasts to every nodes in the next layer. The number of layers is proportional to the number of salient features. As a result, the initial filtered image becomes a low pass image${\tilde{Y}}_k\left(\stackrel{\rightharpoonup }{x},t\right)$ close to emissive LWIR image using the uncooled micro-barometer camera which is apparently invariant to the illumination. The multiple layer deep learning algorithm will eventually reduce the LMS errors $\parallel {\tilde{Y}}_k\left(\stackrel{\rightharpoonup }{x},t\right)-Y_k\left(\stackrel{\rightharpoonup }{x},t\right){\parallel }^2\Rightarrow 0.01$ within 1% of total energy$<\parallel Y_k\left(\stackrel{\rightharpoonup }{x},t\right){\parallel }^2>$ The ANN filtered output ${\tilde{Y}}_k\left(\stackrel{\rightharpoonup }{x},t\right)$ converges eventually after 100 iterations at the desired output $Y_k\left(\stackrel{\rightharpoonup }{x},t\right)$ (LWIR image) when the weights change (Figure 2).
$LMS=\left|\right|{\tilde{Y}}_k\left(\stackrel{\rightharpoonup }{x},t\right)-Y_k\left(\stackrel{\rightharpoonup }{x},t\right){\parallel }^2$

Figure 1 A set of multiple spectral pictures e.g. from Google Cloud Storage, or directly multiple spectral image data bases (DARPA (AFOSR) Human Identification at Distance (HID) 2002-2003collected at National Institute of Standard Technology over 100K faces of 300 people known as the Equinox Corporation Visible/Infrared Face Database(http://www.equinoxsensors.com/hid)with 6 month apart for tracking any aging and emotion effect; For Infrared Faces are peaked Planck blackbody radiation spectrum at 〖37〗^o C which is maximum around 9 μm the center of LWIR ).

Figure 2 Dumb but Fast Deep Learning in Back propagation can utilize the Google day and multiple spectral Infrared images as BDA. Initiate |[$W_{j,k}$ ]|<1 for day image low pass to night image, together with σ-logistic threshold.  The reverse direction of from night pictures to recover the day pictures seems to be difficult as it would require increasing the d. o. f. information content.

Besides the benefit of automation, given real world measurements of day only, we can predict the night image. Moreover, given the pairs day & night images, ANN can capture the ratio of reflectivity of day object surface and the emissivity of LWIR from the object surface. Of course, without knowing the reflectivity and emissivity, a high resolution image of Mag-pixels of 12 bits dynamic range of day image to generate night image becomes formidable job, using Night Vision Image Generator (NVIMG) tool kit of NVESD. The Deep Learning ANN approach may combine both Day and Infrared Images for Aided Target Recognition going beyond DARAP(AFOSR) HID Program F49620-01-C-0008.

Given day Image we shall verify the goodness of ANN predict of night image or equivalent human (Law Enforcement) field Performance metrics. We have split screen computer displaying day & night images, We can verify the ANN generated night image, as well as train law enforcement performance to recognize night face from day face. We shall provide exemplars e.g. John’s pairs & Dave’s pairs; then we add computer generated John’s pairs and Dave’s pairs. We add a mixed up confusion “day John with Night Dave”, or “day Dave with Night John” as follows: (Figure 3)

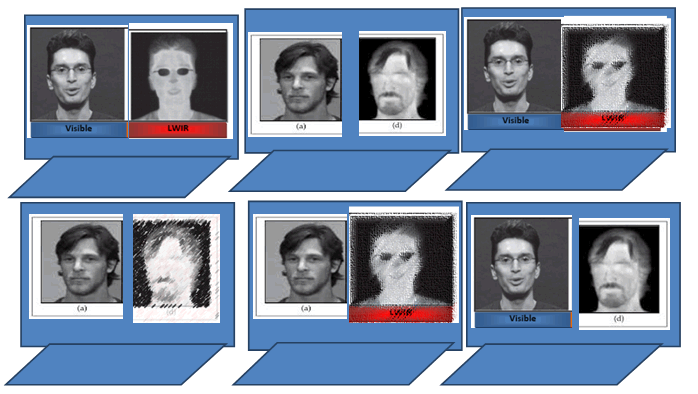
Figure 3 These results can be statistical tabulated to validate the performance of automation of night vision images.

Receiver Operation Characteristic (ROC) is plotting the human observer Probability of Detection (PD) versus False Alarm Rate (FAR) = nuisance False Positive Rate (FPR) + dangerous False Negative Rate (FNR) (Figure 4)

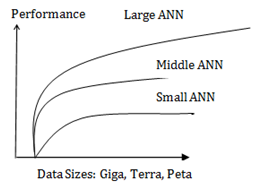
Figure 4

1. ROC Curve plotting probability detection (PD) versus False Alarm Rate (FAR) the error bars variances will be reduced in a small, a medium and a large data sizes using amall medium and large ANN's.
2. Nonlinear Phase Transition of the Performance versus training data sizes (giga, terra, peta bytes). A typical small ANN is 50x50x5layers: medium ANN is: 500x500x10layers, large ANN is: 1000x1000x100layers.  While the assertion is taken from Andrew Ng, Baidu, 2016 You Tube, the explanation is given in our paper. The reason behind may be understood in twofold details: The performance is plotted in (b) along y axis against the training data size along x-axis, over two saturation curves in parameter of the sizes of neural networks (1) small, (2) medium and (3) large.  Both (1) (2) are saturated, except (3) large keep going the performance. We know this reason of indefinite performance is due to quadratic law of interconnect matrix [W_(i,j)] for 3 neurons is 3x3 =9 and n neurons is nxn=n^2 growth. Also, the layer of neural network can also increase to enhance the performance by more gross level features sets are incorporated as more layers are met with lower & lower dynamic range pixels, since both [W_(i,j)]& sigmoid logic are usually less than one as a low resolution/pass filter.

While the assertion is taken from Andrew Ng, Baidu, 2016 You Tube, the explanation is given in our paper. The reason behind may be understood in twofold details: The performance is plotted in (b) along y axis against the training data size along x-axis, over two saturation curves in parameter of the sizes of neural networks (1) small, (2) medium and (3) large. Both (1) (2) are saturated, except (3) large keep going the performance. We know this reason of indefinite performance is due toquadratic law of interconnect matrix$\left[W_{i,j}\right]$ for 3 neurons is 3x3 =9 and n neurons is $nxn=n^2$ growth. Also, the layer of neural network can also increase to enhance the performance by more gross level features sets are incorporated as more layers are met with lower & lower dynamic range pixels, since both$\left[W_{i,j}\right]$ & sigmoid logic are usually less than one as a low resolution/pass filter.

Fusion Image generated by multiple mobile sensors by means of salient orthogonal features

Given Surveillance of Mobile platforms UXV (X=Air, Marine, Ground, Underwater) operated in GPS denied environment. This is partly due to on-board computer deals only with digital pixels information: “the higher the resolution is, the worse the registration becomes.” This is partly due to the lacking of miniaturized local atomic clock on board of jittering platform.

On the other hands, we know from Human Sensory System, where there is no digital representation, the analog representation gives rise to feature sets and them the registration becomes relatively easier, so-to-speak, align right on the bull eye shaving no pixels but features information. Human Visual System (HVS) begins with Learning for the Orthogonal and Normalized (ON) sparse Feature Extraction (FE) at the back of head Cortex 17 area, e.g. layer V1 for color extraction; V2, edge; V3, contour; V4, Texture; V5-V6 etc. for the scale invariant night vision feature extraction for the survival of the species in terms of 150 millions rods arranged uniformly dense in the fovea coordinate X/s, where s is size scale factor. The rod density exponentially decreases from the Center, known as the non-uniform sampling X at the fovea, and uniformly read out U in back of retina toward the cortex 17. Thus, the PEG sampling has archived in real time the scale invariant at the back of the head cortex 17 area. This is known as the polar exponential grid (PEG) algorithm-architecture for a gracefully degradation of image sizes ("Adaptive Invariant Novelty Filters," H.H.Szu & R. A.Messner IEEE Proc.V74, pp.518-519, 1986).

$\frac{X}{s}=\exp \left(U\right);U=LogX-Logs;s=2,Log2=0.3$

 Then, we follow the classifier in the associative learning called Hippocampus AssociativeMemory (HAM). The adjective Deep refers to learning structured hierarchical higher-level abstraction multiple layers of Convolution NNs to a broader class of machine learning to reduce False Alarm Rate. The reason why it is necessary is due to the nuisance False Positive Rate (FPR); but the detrimental False Negative Rate (FNR) could delay the early opportunity. Sometimes one might be over fitting in a subtle way;ANN becomes “brittle” outside the training set. (S. Ohlson: “Deep Learning: How the Mind overrides Experience,” Cambridge Univ. Press 2006.). Thus, BNN requires the growing recruiting and pruning trimming neurons for the self-architectures. We shall extract salient and orthogonal and normalized (ON) sparse features and then registered multiple frames that will be less sensitive to the variations of direct pixel registrations. The ON nature will enjoy fault tolerance. For example, when a child is introduced with Uncle who has a big nose & Aunty who has big eyes (Figure 5). The child forms an ON salient Feature Extraction (FE) for big nose $\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$  and big eye $\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$

$\left[HAM\right]=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\end{array}\right]+\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]$        (1)
When Big nose Uncle smile the feature will be$\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right]$ , the questionto the child will become: “is he or isn’the?”
Hippocampus Associative Memory (HAM) recall is the inner product dispelling the doubt:

$\left[HAM\right]\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]yes,bignoseuncle$                                                     (2)

Figure 5 Hippocampus Associative Memory (HAM) will be defined in sparsely Ortho-Normal Feature (Szu, et al. NN 29-30(2012), pp.1-7).

This is the biological strategy of using sparse independent features (in orthogonal vector representation), explain why the Homosapiens requires the saliency by experiences to prune those irrelevant features for the survival. As such those ON FE can be Fault Tolerant (FT) for one bit error 33% error tolerance; and Abstraction and Generalization are two sides of the same coin that laughing uncle is the same uncle as the NI.

 “Unsupervised Deep Learning (UDL)is theHoly Grail said recently by Prof. Yann LeCun of Courant Institute of NYU in his celebrated You Tube Deep learning Lecture. We believe human being is mostly unsupervised deep learning. As eyes and ears receive the outside excitation energy, the brain will be relaxed toward the thermodynamics equilibrium and in that process we learn the meaning of the excitation. How do we do? Thus, we begin to derive the holy-grail UDL from our brain Biological Neural Network (BNN) involving Glial cells based on Physiology and Physics as a new algorithm.

When Albert Einstein passed away in 1955, biologists wondered what made him smart and kept his brain for subsequent investigation for decades until the discovery of more Glial cells than Neurons. They were surprised to find that his brain weighed about the same as an average human at 3 pounds, and by firing rate conductance measurement the same number of neurons about ten billions as an average person. These facts suggested the hunt remains for the "missing half of Einstein brain." Due to the advent brain imaging (f-MRI based on hemodynamic, based on oxygen utility red blood cells to change from ferromagnetic to diamagnetic when the red blood cell has combined with the oxygen), CT based on micro-calcification of dead cells, PET based on radioactive positron agents), the neurobiology discovered the missing half of Einstein Brain to be the non-conducting Glial Cells (In Greek: Glue cells made mostly of fatty acids) that is smaller in size about 1/10th of the size of a neuron, but doing all the work by keeping ions in line with nowhere to go but within axons to achieve real time communication with firing rates. Now we know a brain takes two to tango: “billions neurons (gray matter) and hundred billions Glial cells (white matter).” (Figure 6) Eistein seemed to have more Glial cells to keep ions in line to go through rapidly the neuron synapses (Figure 7).

Figure 6 A) Albert Einstein at Princeton Inst. of Adv. Studies
B) NY World Telegram reported his death at age 76
 C) His brain was kept in formaldehyde jar for studies then the glial cells surround neurons and provide support for and insulation between them. Glial cells are the most abundant cell types in the central nervous system.

Figure 7 Apparently Einstein has more glial cells to keep ion vesicles in line and rapidly passing though the axon to other neurons Neuron firing vesicles, about 100 ions per sec, of which each ion is 1000 times bigger than an electron, like slow ducks line up crossing the road. While one ion pops in, the other pops out. Missing Half of Einstein Brain is the 100 B glial cells, which surround each axon as the white matter (fatty acids) that keep slow neuron transmits ions fast. The more (Oligodendrocytes Myelin Sheath) Gial cells Einstein has, the faster neuron communication, Einstein brain can.  Thus, if one can be fast to explore all possible solution, one will not make hasty decision.

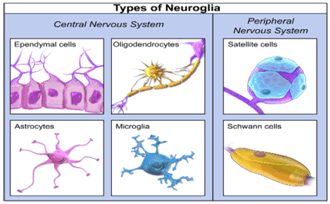
Figure 8 Functionality: They surround each neuron Axon output, in order to keep the slow neural transmit ions line up inside the Axon tube, so that one pushes in the other pushes out in real time.  There are more functionality provides nutrients. Neuroglial Biology insures 4 functionalities:

1. Real Time (RT) Communication because Axon ion vesicles are confined and aligned up in Axon Cable surrounded by electrically insulated White Matter Myelin Sheath Glial Cells making axon insulator an co-axial cable, becoming “how the duck cross the road?” O(Δt)=10-th mille-sec. One meter long from the tail end of the spinal cord to the big toe running away for the survival of the species.;
2. Multiple layer Convex Hull Classifier reduce False Alarm Rate; (3)Multiple Morphology Multiple Neuroglial
3. Neurological disorder at the singularity of glial cells may define the brain tumor Glioma. This image shows the four different types of glial cells found in the central nervous system: Ependymal cells (light pink), Astrocytes (green), Microglial cells (red), and Oligodendrocytes (functionally similar to Schwann cells in the PNS) (light blue). (By Artwork by Holly Fischer.

There are 6 kinds Glial cells (about one tenth in the size compared with Neurons; 4 kinds in CNS(Astrocytes, Microglia, Ependymal, Oligodendrocytes Myelin Sheath); two in Spinal Core: (Satellite, Schwann). (Figure 8) They are more than silent partners as housekeeping servant cells (Figure 9)(Table 1).

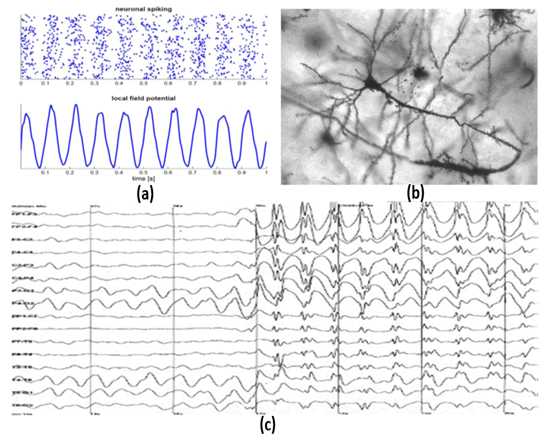
Figure 9 Epileptic seizures

1. Neurons population fired in bundles, due to Hebb observation "wired together, fired together.  Thus, the population density of firing varies like a wave
2. Laser can burn off the axon feedback knot at dendrite.
3. Time from the left to the right, the phase transition resulted in the epileptic seizure from excessive positive feedback gain instability of neuronal feedback.

Table 1 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion

Looking deeper into deep learning. Elucidating EEG brainwaves at the onset of Epileptic Seizure may shed the light on firing spiking population & local field potential for the phase transition of the Helmholtz Free Energy (Szu et al SPIE News 2015). We have EEG brain waves; why we do not have the Neurodynamics wave equation? It takes 10 billion neurons & 100 billion nuroglial (Greek: Glue) cells to Tango. Of course the number of 100 billion is due to putting all 6 types Neuroglia cells together. What is Biological Neural Networks (BNN)? A slow Alzheimer dementia is because of without a good night sleep Astrocytes (Neuroglial cells)are blocked by energy by-product waste beta Amyloids. As all city trash collectors are operated in the night without traffic jams.

The traditional approach of SDL is solely based on multiple layers of Neurons as Processor Elements (PE) or Node of ANN. Instead of SDL training cost, function the Lease Mean Squares, using Least Mean Squares (LMS) Error Energy,

$E=|(desiredOutput{\stackrel{\rightharpoonup }{S}}_{pairs}-acturalOutput{\widehat{S}}_{pairs}\left(t\right){|}^2$ (3)

Sensory unknown Inputs

Power of Pairs:${\stackrel{\rightharpoonup }{X}}_{pairs}\left(t\right)=\left[A_{ij}\right]{\stackrel{\rightharpoonup }{S}}_{pairs}\left(t\right)$ (4)

where the agreed signals form the vector pair time series${\stackrel{\rightharpoonup }{X}}_{pairs}\left(t\right).$

Recently, Smartphone has implicated to wear a wireless head mount during Yoga , Tai Chi Quan which can stimulate the 10th cranial Vegas nerve to Alpha, Theta for PTSD monitor (TBD, NIMH) Sleep Tight for Astrocytes Neuroglial cells cleaning 20% energy by-products, e.g. beta-Amyloids junks, to Glymphatic system of Brain Blood Barriers (Figure 10).

Figure 10 Visual Cortex Brodmann Areas (BA) 17 (Red Primary), 18(orange), 19(yellow) (left) and Info flow paths (middle); BA17 Occipital lobe has Dorsal stream V1,V2, V5: where & how eyes &arms; & Ventral stream V1 V2 V4 what LTM).

We shall return to the fact that the uniformity of neuronal firing rate population may be measurable by the Boltzmann Entropy S. for a broader Natural Intelligence (NI). We shall introduce a novel concept of the internal state representation of the degree of uniformity of group of neurons’ firing rates:$S_{pairs}\left(t\right)$ ,which may be described with Ludwig Boltzmann entropy with unknown space-variant impulse response functions mixing matrix$\left[A_{{}_i}{}_{{}_j}\right]$ and the inversion is by means of learning synaptic weight matrix
Convolution Neural Networks:${\tilde{S}}_{pairs}\left(t\right)=\left[W_{ji}\left(t\right)\right]{\stackrel{\rightharpoonup }{X}}_{pairs}\left(t\right)$ (5)
The unknown environmental mixing matrix is denoted$\left[A_{{}_{i,j}}\right]$ . The inverse is the space-variant Convolutional Neural Network weight matrix $\left[W_{ji}\right]$ of general type that can generate the internal states of knowledge representation.
Our unique and the only assumption, which is similar to early Hinton’s Boltzmann Machine, is the measure of degree of uniformity about the histogram or population of neuronal firing rates Internal States known as the Entropy, introduced first by Ludwig Boltzmann (Figure 11).

Figure 11

1. Power of Pairs keep concurent signals as information
2. filter out the diagreement as the noise and relax the local excitation into thermodynamic equilibrium
3. The information is kept in wavelets, or multiple resolution analysis (MRA)The beauty is in the eyes of beholder those who are in love are blind in a low resoltuion.

ANN is a MPD storage for the fault tolerant nearest neighbor classifier. We begin with the uniform average. We then do it recursively. We obtain a faster convergence by adding the difference between new comer data with respect to the old averaged centroid. When Kalman has generalized the uniform average with a weight average, the constant numerical value becomes a variable Kalman filtering. Furthermore, the weighted Kalman filtering is generalized with a “learnable recursive average” called the single layer of Artificial Neural Network, or Kohonen Self Organization Map (SOM), or Carpenter-Grossberg “follow the leader Adaptive Resonance Theory (ART). This mathematics is relatively well known in the early recursive signal processing. The new logic of ANN is augmented with a threshold logic at each processing elements (PE) or neuron nodes based on these three operations:

AVERAGING:

${\overline{x}}^N\equiv \frac{1}{N}{\sum }_{i=1}^N{x}_i\Rightarrow <x{>}_N=\frac{1}{{{\displaystyle \sum w_i}}^{\text{}}}{\sum }_{i=1}^N{w}_i{x}_i;$       (6)

SMOOTHING:

${\overline{x}}^{N+1}\equiv \frac{1}{N+1}{\sum }_{i=1}^{N+1}{x}_i=\frac{N+1-1}{N+1}\frac{1}{N}{\sum }_{i=1}^N{x}_i+\frac{1}{N+1}{x}_{{}_{N+1}}={\overline{x}}^N+\frac{1}{N+1}\left(x_{N+1}-{\overline{x}}^N\right)$   (7)

PREDICTION:

$<x{>}_{N+1}=<x{>}_N+K\left(x_{N+1}-<x{>}_N\right),$                                          (8)

where we have used

$C=\frac{A+B}{2}=A+\frac{1}{2}\left(B-A\right)$                                                                (9)

This is why we replace the average mean by add the difference between the new input data with respect to the old averaged mean. It is in this spirit that Kalman has introduced the gain when the average is no longer the uniform average but a weighted average (Figure 12).
Furthermore, Artificial Neural Networks introduce the redundant outer and inner productat Hippocampus Associative Memory [HAM]. A column vector of three components represents three neuron, the outer products describes the nine communication synaptic matrix among three neuron. Mathematics is the outer product

$\left[\begin{array}{c}{n}_1\\ n_2\\ n_3\end{array}\right]\left[\begin{array}{ccc}{n}_1& n_2& n_3\end{array}\right]=\left[\begin{array}{ccc}{n}_1{n}_1& n_1{n}_2& n_1{n}_3\\ n_2{n}_1& n_2{n}_2& n_2{n}_3\\ n_3{n}_1& n_3{n}_2& n_3{n}_3\end{array}\right]=\left[HAM\right]=\left[W_{i,j}\right]$ (10)

Read by Inner product after the nearest neighbor classifier threshold (Th)

Why we need Deep Learning? $\left[\begin{array}{c}{n}_1\\ n_2\\ n_3\end{array}\right]\left[\begin{array}{ccc}{n}_1& n_2& n_3\end{array}\right]=\left[\begin{array}{ccc}{n}_1{n}_1& n_1{n}_2& n_1{n}_3\\ n_2{n}_1& n_2{n}_2& n_2{n}_3\\ n_3{n}_1& n_3{n}_2& n_3{n}_3\end{array}\right]=$ $Th.\left[\begin{array}{c}{n}_1\\ n_2\\ n_3\end{array}\right]$ (11)

Figure 12 Two ways to update the Centroid: The centroid vector $\stackrel{\rightharpoonup }{C}$ may be computed in Eq(7) from the old centroid vector $\stackrel{\rightharpoonup }{A}$  and the new data $\stackrel{\rightharpoonup }{B}$  that is different from the old centroid ($\stackrel{\rightharpoonup }{B}$ -$\stackrel{\rightharpoonup }{C}$ ).  This may be called the following the leader $\stackrel{\rightharpoonup }{A}$  becoming new leader $\stackrel{\rightharpoonup }{C}$ which is the Centroid$\frac{\stackrel{\rightharpoonup }{A}+\stackrel{\rightharpoonup }{B}}{2}$ .

The reason of why the ANN requires multiple layers of neurons, as the so-called “Deep Learning.” Other than higher order extraction, there are mathematical reason to reduce False Alarm Rate (FAR): This is because multiple layers can refine the single layer linear classifier to multiple layer convex hall classifier (Figure 13).

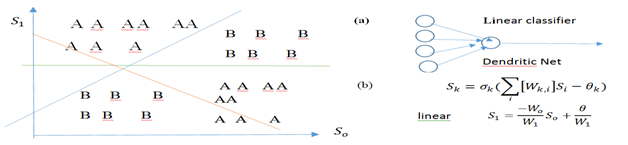
Figure 13 Artificial Neural Networks (ANN) need multiple layers known as Deep Learning to reduce the False Alarm Rates (FAR).

1. Left panel shows that while a single layer of Artificial Neural Network can simply be a linear classifier shown in the Right Panel
2. Multiple layers can improve the FAR denoted by symbol “A” included in the second class B.

Obviously, it will take at least three linear classifier layers to completely separate both the mixed classes: A and B. When there are more than two salient features, one would need a lot more layers. That is why commercial MPD super computers have claimed nearly 100 layers of ten’s thousands nodes per layer in order to do computational intelligence. (cf. R. P. Lipmann IEEE ASSP Mag Apr.1987).

Natural Intelligence (NI) is a kind of CI based on two necessary and sufficient principles observed from the common physiology of all animal brains (Sze et al., circa 1990) The key is to introduce to determinethe physics representation of the internal degree of freedom.

Homeostasis thermodynamic principle

All animals roaming on the Earth have isothermal brains operated at a constant temperature$T_o$ , (Homosapiens 37oC for the optimum elasticity of hemoglobin, Chicken 40oC for hatching eggs)

1. Power of pairs

All isothermal brains have pairs of input sensors ${\stackrel{\rightharpoonup }{X}}_{pairs}$ for the co-incidence account to de-noise: “agreed, the signals; disagreed, the noises,” for instantaneously processing (Figure 14) (Figure 15).

1. Total Entropy:$S_{tot}=k_B\log W_{MB}$                                                                               (13)

Solving Eq (13) for the phase space volumeW_MB, we derive the Maxwell-Boltzmann (MB) canonical probability for isothermal system

2. $W_{MB}=\exp \left(\frac{S_{tot}}{k_B}\right)=\exp \left(\frac{\left(S_{brain}+S_{env.}\right)T_o}{k_B{T}_o}\right)=\exp \left(\frac{S_{brain}{T}_o-E_{brain}}{k_B{T}_o}\right)=\exp \left(-\frac{H_{brain}}{k_B{T}_o}\right)$    (14)

(Figure 16) Use is made of the isothermal equilibrium of brain in the heat reservoir at the homeostasis temperature$T_o$ . Use is also used of the second law of conservation energy $\Delta Q_{env.}=T_o\Delta S_{env.}$ and the brain internal energy$\Delta E_{brain}+\Delta Q_{env.}=0$ , and then we integrate the change and dropped the integration constant due to arbitrary probability normalization. Since there are numerous neuron-firing rates, the set of scalar entropy becomes the vector entropy for the representation of internal states the degree of uniformity clusters of neuronal firing rates.

$\left\{S_j\right\}\iff \stackrel{\rightharpoonup }{S}$(15)

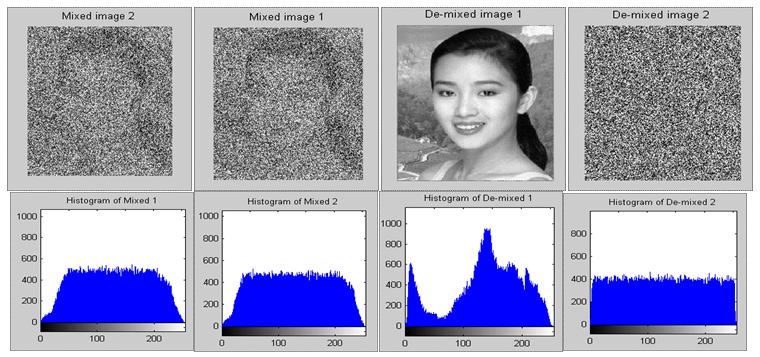
Figure 14 Power of Pairs indicate the agreed noisy image pixel can be separate those who are agreed as the signal image, while the disagreements are noise values.

Boltzmann defined the Entropy to be"a measure of the degree of uniformity."a large uniformity has a large entropy. QUIZ: Which objects have a larger entropy?

Figure 15 Sands or Rocks? (Clue: erosion & heat death).

Figure 16 Ludwig Boltzmann  S=k log W.

Biologists might ask the reason why the Entropy defined by Boltzmann is a proper measure of the degree of uniformity voting consensus of neuron firing rates population. Historically speaking, Boltzmann committed suicide and written on his headstone was only his immortal formula that he has argued with Henri Poincare about; not even his name was on the headstone. In 1912, Walter Nernst stated the third law of thermodynamics: "It is impossible for any procedure to lead to the isotherm T= 0 in a finite number of steps.” Since Kelvin temperature can never reach the absolute zero, an incessant molecular collisions will mix toward maximum uniformity as the heat death as Boltzmann basis of the irreversible increase of the entropy toward the heat death. In other words, molecular collision will gradually erode the binging energy, the loss of archeology information dear to paleontologist at hearts, e.g. a landslide voting has maximum uniformity associated with no voter distribution information. Therefore, we assert that the physics entropy becomes an appropriate internal state of knowledge representation (ISKR). Boltzmann dis-information is Shannon information.

1. Henri Poincare observed keenly that all the dynamics both classical Newtonian and quantum mechanical is time reversible invariant$\left(t\iff -t\right)$

$m_o\frac{d^2\overrightarrow{X}}{d{t}^2}=m_o\frac{d^2\overrightarrow{X}}{d{\left(-t\right)}^2}$;$\pm i\hslash \frac{\partial \text{Ψ}}{\partial \left(\pm t\right)}=-\frac{{\hslash }^2}{2m}{\nabla }^2\text{Ψ}$

2. We now know after all Boltzmann is right, the trajectory is more than dynamics but initial boundary conditions, which are time irreversible variant due to collision mixing.

$\Delta S_{tot}>0$                                                                                                 (16)

3. Can assert brain NI learning rule

$\Delta H_{brain}=\Delta E_{brain}-T_o\Delta S_{brain}\le 0$ .                                                       (17)
This is NI cost function at MFE useful in the most intuitive decision for Aided Target Recognition (Air) at Maximum PD and Minimum FNR for Darwinian natural selection survival reasons. The survival NI is intuitively simple, fight or flight, Parasympathetic nerve system as an auto-pilot. Maxwell-Boltzmann equilibrium probability is derived early in Eq(13) in terms of the exponential weighted Helmholtz Free Energy of brain: (Figure 17)
$H_{brain}=E_{brain}-T_o{S}_{brain}$  (18)
Note that Russian Mathematician G. Cybenko has proved “Approximation by Superposition of a Sigmoidal Functions,” Math. Control Signals Sys. (1989)2: 303-314. Similarly, AN Kolmogorov, “On the representation of continuous functions of many variables by superposition of continuous function of one variable and addition, Dokl. Akad. Nauk, SSSR, 114(1957), 953-956.

Figure 17 Hermann Helmholtz.

Theorem of unsupervised learning

 The unsupervised learning follows Maxwell-Boltzmann canonical probability that relaxes merely the inputs the excited brain energy toward the isothermal equilibrium brain.
Proof:

$\frac{\exp \left(-\frac{H_{brain}^{*}}{k_B{T}_o}\right)}{\exp \left(-\frac{H_{brain}^{*}}{k_B{T}_o}\right)+\exp \left(-\frac{H_{brain}}{k_B{T}_o}\right)}=\frac{1}{1+\exp \left(-\frac{\Delta {\text{H}}_{brain}}{k_B{T}_o}\right)}\equiv \sigma \left(\frac{\Delta {\text{H}}_{brain}}{k_B{T}_o}\right)=\{\begin{array}{c}1,\frac{\Delta {\text{H}}_{brain}}{k_B{T}_o}\to \infty \\ 0,\frac{\Delta {\text{H}}_{brain}}{k_B{T}_o}\to -\infty \end{array}$  (19a)

Thus the normalization of Maxwell-Boltzmann canonical probability ratio turns out to be the logistic logic which is merely the two state normalization of Maxwell-Boltzmann probability$\Delta H_{brain}=H^{*}{}_{brain}-H_{brain}>0$ >

Q.E.D.

Theorem of Change of Unsupervised learning in a Window Function

$\frac{d\sigma \left(H_{brain}\right)}{d{H}_{brain}}=\sigma \left(H_{brain}\right)\left\{1-\sigma \left(H_{brain}\right)\right\}$                                                                                                          (19b)

Proof:$y=\sigma \left(x\right)\equiv {[1+\exp \left(-x\right)]}^{-1}$
$\frac{dy}{dx}={[1+\exp \left(-x\right)]}^{-2}\exp \left(-x\right){(-1)}^2=\left[1+\exp \left(-x\right){]}^{-2}[\exp \left(-x\right)+1-1\right]=\sigma \left(x\right)-\sigma {\left(x\right)}^2$ . Q.E.D.

Theorem of morphological changing of brain energy consumption might be the decision factor.
$\frac{\exp \left(-\frac{H_{prune}}{k_B{T}_o}\right)}{\exp \left(-\frac{H_{prune}}{k_B{T}_o}\right)+\exp \left(-\frac{H_{recruit}}{k_B{T}_o}\right)}=\frac{1}{1+\exp \left(-\frac{\Delta {\text{H}}_{\text{brain}}}{k_B{T}_o}\right)}\equiv \sigma \left(\frac{\Delta {\text{H}}_{\text{brain}}}{k_B{T}_o}\right)=\{\begin{array}{c}1,\frac{\Delta \Delta {\text{H}}_{\text{brain}}}{k_B{T}_o}\to \infty \\ 0,\frac{\Delta {\text{H}}_{\text{brain}}}{k_B{T}_o}\to -\infty \end{array}$   (19c)
Q.E.D.

We have suggested the positive growing brain shall recruit Stimulated Pluripotent stem cell to differentiate symbiotically into a new neurons and a new glial cells (or prune old neurons that cost too much energy to maintain). Consequently, a brain has left with smaller glial cells about one tenth of a neuron and costs a lot less the energy as glial does not itself firing calcium ions. Thus, a node will be determine to be pruned or recruited depends on the local brain energy difference. The slope of brain energy sigmoid function is merely a window function near the prune or recruit equilibrium connect or not as:$\Delta {\text{H}}_{\text{brain}}\equiv {\text{H}}_{\text{prune}}-{\text{H}}_{\text{recruit}}$ waited by Homeostasis equilibrium energy$k_B{T}_o=\frac{1}{50}eV$ , for$T_o=300K$ . Homosapiens prefers at 37oC for it is optimum for red blood cell, hemoglobin, whose elasticity is required to squeeze through capillary without leaving oxygen or carbon oxides behind; while Chicken is kept at 40oC that might be compromised for their egg hatching. It is, however, not the Homeostasis temperature value per se, but a higher temperature did not implicate more intelligence. Evolutionally phenome-typical speaking, chicken are lacking of their big thumb for holding tools becomes less intelligent than Homosapiens (we ate them, not vice versa, Q.E.D.).

Derivation of Newtonian equation of motion the Biological Neural Networks (BNN) from the Russian Mathematician Aleksandr Mikhailovich Lyapunov (Figure 18) who has proved a monotonic absolute convergence theorem as follows: Since an equilibrium brain at MFE$\Delta H_{brain}\le 0$ must be guaranteed by the negative of square power of synaptic weight changes Eq(20)(Figure 18).

$\frac{\Delta H_{brain}}{\Delta t}=\left(\frac{\Delta H_{brain}}{\Delta \left[W_{i,j}\right]}\right)\frac{\Delta \left[W_{i,j}\right]}{\Delta t}=-\frac{\Delta \left[W_{i,j}\right]}{\Delta t}\frac{\Delta \left[W_{i,j}\right]}{\Delta t}=-{(\frac{\Delta \left[W_{i,j}\right]}{\Delta t})}^2\le 0$ Q.E.D.              (20)
Therefore, Neurodynamics is merely Newtonian (Figure 19) equation of motionEq(21) for the learning of synaptic weight matrix which follows from thebrain equilibrium at Helmholtzminimum free energy (MFE)

$\frac{\Delta \left[W_{i,j}\right]}{\Delta t}=-\frac{\Delta H_{brain}}{\Delta \left[W_{i,j}\right]}$                                                                                                                                             (21)
It takes two to Tango. Unsupervised Learning becomes possible because BNN has both Neuronsas threshold logic and house keeping Glial cells as input Dendrite and output ion firing rate.

We assume for the sake of the causality, the layers are hidden from the outside direct input, except the first layer, and the l-the layer can flow forward to the layer l+one, or backward, to l-1 layer, etc.

Figure 18 Russian Mathematician A. M. Lyaponov

Figure 19 British Physicist Isaac Newton

We define the Dendrite Sum from all the firing rate ${\stackrel{\rightharpoonup }{S}}_i$ of lower input layer represented by the output degree of uniformity entropy ${\stackrel{\rightharpoonup }{S}}_i$ as the following net Dendrite vector:
${\stackrel{\rightharpoonup }{Dendrite}}_j\equiv {\sum }_i\left[W_{i,j}\right]{\stackrel{\rightharpoonup }{S}}_i$                                                                                      (22)
Canadian Neurophysiologist D.O. Hebb 1949 a half Century ago obtained the learning rule observed that neurons obey the principle that neurons whichfire together are wired together(FTWT)" (WTFT) the co-firing of the presynaptic activity and the post-synaptic activity (Figure 20)

Figure 20 Canadian Neurobiologist Donald O. Hebb.

Hebb observed the conservation of lawthat neurons that fire together wire together(FTWT) namely the product $\frac{\Delta {\stackrel{\rightharpoonup }{Dendrite}}_j}{\Delta \left[W_{i,j}\right]}\equiv {\stackrel{\rightharpoonup }{S}}_i$ between the postsynaptic outputs firing rate${\stackrel{\rightharpoonup }{S}}_i$ , e.g. 100 calcium ions $C{a}^{++}$ per second, must be proceed with the presynaptic glial cells shuttling through dendrite tree. This Hebb Learning Rule observation of WTFT has forced us to fire ${\stackrel{\rightharpoonup }{S}}_i$ i by introducing the mathematical definition of biological Glialcells${\stackrel{\rightharpoonup }{g}}_j$ Eq(23). Historically speaking, pathologist Rudolf Virchow discovered Glial cells in 1856 in his search for a connective tissue in the brain.Thus, the name Glial (Greek: Glue) implicates those housekeeping supportive cells in the central nervous system. Unlike neurons, Glial cells are fatty acids white matter that do not conduct electrical impulses. There are six types of such property Glial cells surrounding neurons and provide the insulation & glue support between them. Six types of Glial cells are known in different names: oligodendrocytes, astrocytes, ependymal cells, Schwann cells, microglia, and satellite cells. Putting it all together, Glial cells become the most abundant cell types in the central nervous system about 100 billion. We can provide a unified theory of all, due to six different morphologies of both the Dendrites and the axon. The output firing ions must be recruited from the synaptic gap matrix connected through the dendrite tree to all other ends ions. From Newtonian-like, equation Eq (21) right hand side (RHS) follows the Glial definition Eq(23)

If$\frac{\Delta \left[W_{i,j}\right]}{\Delta t}\equiv -\frac{\Delta {\text{H}}_{brain}}{\Delta \left[W_{i,j}\right]}=\left(-\frac{\Delta {\text{H}}_{brain}}{\Delta {\stackrel{\rightharpoonup }{Dendrite}}_j}\right)\frac{\Delta {\stackrel{\rightharpoonup }{Dendrite}}_j}{\Delta \left[W_{i,j}\right]}\equiv {\stackrel{\rightharpoonup }{g}}_j{\stackrel{\rightharpoonup }{s}}_i$ (23a)

The necessary of Hebb "FTWT firing " forcedus to define the MFE slope w.r.t. the as the input facilitator Glials cells.

Then

$\left(-\frac{\Delta {\text{H}}_{brain}}{\Delta {\stackrel{\rightharpoonup }{Dendrite}}_j}\right)\equiv {\stackrel{\rightharpoonup }{g}}_j$                                                                                (23b)

The mathematical singularity of a too strong glue force is analogous to gravitational attraction force that produces a black hole when there is too much mass, the biological equivalent is thatcoagulated dendrites cells material lumptogether to form a solid lump tumor known as the biological cancer disorder
${\stackrel{\rightharpoonup }{g}}_j=-\frac{\Delta H_{brain}}{\Delta {\text{dendrite}}_j}\to \infty$ Glioma (24)
We can expand the mathematical definition of Glial in a Taylor series
${\stackrel{\rightharpoonup }{g}}_j={\stackrel{\rightharpoonup }{g}}_j^{\left(o\right)}+\frac{\partial {\stackrel{\rightharpoonup }{g}}_j}{\partial {\text{dendrite}}_{\beta }}{|}^{\left(o\right)}\left({\text{dendrite}}_{\beta }-{\text{dendrite}}_{\beta }^{\left(o\right)}\right)+O\left({\text{Δ}}^2\right)$                     

The result Eq(24) helps us analytically exam the behavior of Glial cells, to determine the stages of brain tumors.

A glioma is a type of tumor that starts in the brain or spine. It is called a glioma because it arises from glial cells. The most common site of gliomas is the brain. Gliomas make up about 30% of all brain and central nervous system tumors and 80% of all malignant brain tumors (Figure 21).

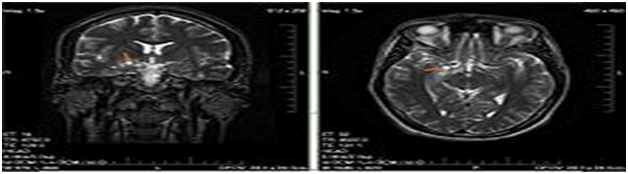
Figure 21 CT scan of Glioma of the left parietal lobe (with contrast enhancement). According to WHO, glioma is classified by grades & locations.  WHO grade <2 glioma are benign but incurable, recurrent, & progressively worse. WHO grade >2 Glioma are malign. The group comprises anaplastic astrocytoma’s and glioblastoma multiform. Whereas the median overall survival of anaplastic (WHO grade III) gliomas is approximately 3 years, glioblastoma multiformhas a poor median overall survival of ~15 months). Epigenetic repression of DNA repair, e.g. consuming diets high in nitrites and low in vitamin C, cell phone EM radiation(Wikipedia edited on 27 April 2017).

Acid oligodendrocytes glial cells these types of glial cells are making those positive charge large ions that repel one From brain medical image, (f-MRI oxygen-utility Hemodynamics, PET contrast-agency, CAT micro-calcification pixel intensity), we can derive the Helmholtz minimum free energy (MFE) by means of Taylor expansion of Internal Energy E in terms of input brain imaging intensity$X_k$ , Then we can computer the negative slope MFE as the glial cells behavior.

Then we can assume the medical image data $\overrightarrow{X}(r,t)=[A]\stackrel{\rightharpoonup }{S}(r,t)$ is related with respect to the unknown impulse response function of the averaged dynamics neuronal population firing rates in terms of the discrete internal representation entropy.

This negative MFE slope has been called the Lagrange Constraint () Neural Networks (LCNN) where the Lagrange is the biological glial cells used to solve Blind Sources Separation by single layer of ANN (Harold Szu, Lidan Miao, Hairong Qi, “Unsupervised Learning with Mini Free Energy,” SPIE Proc. Vol. 6576,pp.1-14, 2007). The white matter glial cells are vital to brain physiology. The growth and the strength of the glue force are critical for brain order and disorder diagnoses. Thus, we shall Taylor expand the glial force in terms of medical image pixel $X_k\left(x,t\right)$  in Eq.(24). WWII Kurush Kuhn Tucker (KKT) have developed an Augmented Lagrange Methodology to solve a higher order perturbation theory. (loc cit Szu et al SPIE 2007)

The Glial cells are fatty acids known as the white matter in the nervous system (CNSbrain and PNSSpinal cord). They wrap around the axon with insulating Myelin Sheath fatty another can transmit meter-long Axon cable from tail to toe.

An autoimmune disease is in which the immune system attacks joints, or eats away at the protective covering of nerves, e.g. Rheumatoid Arthritis pain or Multiple Sclerosis. Damaged nerve covering leads to nerve impulse disruption, e.g. Bladder Dysfunction, Bowel Problems, Crippling Mobility and Double vision, known as the. Normal nerve covering looks like. "One ion pops in, the other ion pops out in a pseudo-real time, as “slow and big ducks line up crossing the road, one enters the road, the other crosses over" if they are forced by Glial cells inside the axon pipeline The longest axon from the end of the spinal cord to the big toe which our ancestors can nevertheless “fight of flight” in real time running away from those tigers or lions.

As we note that, the isomorphism between AI ANN algorithm and NI BNN algorithm allow us to apply Artificial Intelligence Machine Deep Learning to help NI BNN, because BNN can be sick and ANN will not. Thus the crossover can be exceeding helpful to drug data mining and for early diagnosis saving patient from suffering.

Explicitly, we relate the pre-synapse junction development depends on assistance from the glial cells for alternating the resting potential 75mV for glutamine release. Glial cells growth factor deficiency may link to brain disorder such as Schizophrenia.

The Hodgkin–Huxley model, or conductance-based model, is a mathematical model similar to our mathematical definition of glial cells that can describes how glial cells influence the action potentials generated in neurons are initiated and propagated, that approximates the electrical characteristics of excitable cells such as neurons and cardiac myocytes in 1952 to explain the ionic mechanisms underlying the initiation and propagation of action potentials in the squid giant axon. They received the 1963 Nobel Prize in Physiology or Medicine for this work (Figure 22).

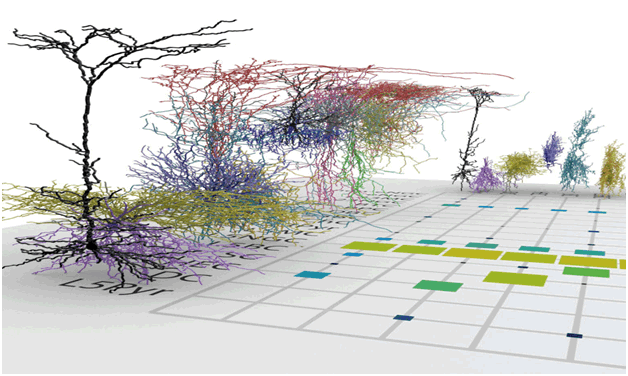
Figure 22 Adult Mice brain Cells: Xiaolong Jiang and Andreas Tolias at Baylor College of Medicine in Houston announced six new types of 15 adult mice brain cells by the method of slicing razor-thin slices (rts) of mature brain. That rts methodology has established a complete census of all neuron cell types is of great importance in moving the field of neuroscience forward," says Tolias, at Baylor College of Medicine   Gray Matter Neurons (William Herkewitz, Science Nov 26, 2015)

Glial Cells, like Neuron Cells, Share the same cellular biology

(Figure 23) The idea that Glial cells might have a role in learning seems contrary to the usual model of dendrite input $\Rightarrow$ soma summation$\Rightarrow$ action potential generation. Neurons are large, tree-like structures with extensive, branch-like dendrites spanning $\Rightarrow$ 1000 μm, but a small ~10-μm soma.
For example: a classical electron radius
$\frac{e}{r}e=E=m{C}^2;r=\frac{e^2}{m{C}^2}=2.8x{10}^{-13}$ cm
$g_j=-\frac{\Delta H}{\Delta D_j}$ ;$D_j={\sum }_k\left[W_{jk}\right]S_k$ ;
$\left|g_j\left|=0.1\right|Neuron\right|=\frac{\left|\Delta H\right|}{\left|\Delta D_j\right|}$ ;
$\left|\Delta H\right|=0.1\left|Neuron\right|\left|\Delta D_j\right|$
$\left|\Delta D_j\right|=10\frac{\left|\Delta H\right|}{\left|neuron\right|}$

It is recently determine Dendrite to be active about 100 times bigger about 1000 μm than soma cell about 10 μm, and so is the action potential (Moore et al. Sci. 2017).

Figure 23 A biological cell has all property of genetic and epigenetic.

"Dendrites receive inputs from other neurons, and the electrical activity of dendrites determines synaptic connectivity, neural computations, and learning. The prevailing belief has been that dendrites are passive; they merely send synaptic currents to the soma, which integrates the inputs to generate an electrical impulse, called an action potential or somatic spike, thought to be the fundamental unit of neural computation. These ideas have not been directly tested because traditional electrodes, which puncture the dendrite to measure dendrite voltages in vitro, do not work in vivo due to constant movement of the animals that kills the punctured dendrites.Hence, the voltage dynamics of distal dendrites, constituting the vast majority of neural tissue, is unknown during natural behavior. Dendrites occupy more than 90% of neuronal tissue. However, it has not been possible to measure distal dendrite membrane potential and spiking in vivo over a long period of time. Moore et al. (Sci. 2017) developed a technique to record the subthreshold membrane potential and spikes from neocortical distal dendrites in freely behaving animals. These recordings were very stable, providing data from a single dendrite for up to 4 days. Unexpectedly, distal dendrites generated 100 times larger action potentials whose firing rate was nearly five times greater than at the cell body. Further Glial cell's with their insulating properties, suggest dynamics with a long time constant. This article (Moore, 2017), however, Neural activity in vivo is primarily measured using extracellular somatic spikes, which provide limited information about neural computation. Hence, it is necessary to record from neuronal dendrites, which can generate dendritic action potentials (DAPs) in vitro, which can profoundly influence neural computation and plasticity. We measured neocortical sub- and supra-threshold dendritic membrane potential (DMP) from putative distal-most dendrites using tetrodes in freely behaving rats over multiple days with a high degree of stability and sub-millisecond temporal resolution. DAP firing rates were several-fold larger than somatic rates. DAP rates were also modulated by subthreshold DMP fluctuations, which were far larger than DAP amplitude, indicating hybrid, analog-digital coding in the dendrites. Parietal DAP and DMP exhibited egocentric spatial maps comparable to pyramidal neurons. These results have important implications for neural coding and plasticity. Tetrodes are a bundle of four fine electrodes, commonly used for measuring somatic spikes from a distance, that is, extracellularly. Hence, they work well in freely behaving animals. However, tetrodes do not measure the membrane voltages of soma, let alone dendrites. Chronically implanted tetrodes also elicit a naturally occurring immune response, where glial cells encapsulate the tetrode and shield it from the extracellular medium. We tested the hypothesis that a segment of dendrite could get trapped between the tetrode tips before this glial encapsulation occurred (figure). This would enable us to measure the dendritic membrane voltage without penetrating it in freely behaving subjects (Figure 24)."

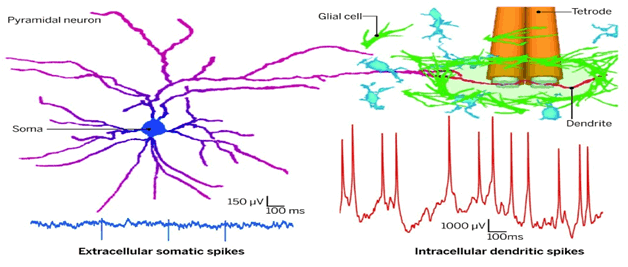
Figure 24 Dynamics of cortical dendritic membrane potential and spikes in freely behaving rats, Jason J. Moore, Pascal M. Ravassard, David Ho, Lavanya Acharya, Ashley L. Kees Cliff Vuong, Mayank R. Mehta, Science 355 (6331). 2017 Mar 09. 

It shows experimental evidence of action potential formation in dendrites. Moore's paper lends support to our theory for a Glial cell role in learning, at least as an abstraction. The performance cost function should be the natural unsupervised MFE, instead of supervised LMS error metric.

Summary:

Unsupervised Deep Learning $\text{MFE}=\Delta {\text{H}}_{\text{brain}}\equiv \Delta {\text{E}}_{\text{brain}}-{\text{T}}_{\text{o}}\Delta {\text{S}}_{\text{brain}}\le 0$  Supervised Deep Learning LMS $\text{min}\text{.}\parallel \text{desired}-\text{actural}{\parallel }^2\ge 0$ . We can interchange MFE with LMS throughout the following set of equations:

1. Lyaponov absolute convergence demands the negative of positive square

$\frac{\Delta {\text{H}}_{brain}}{\Delta \text{t}}=\left(\frac{\Delta {\text{H}}_{brain}}{\Delta \left[{\text{W}}_{\text{i},\text{j}}\right]}\right)\frac{\Delta \left[{\text{W}}_{\text{i},\text{j}}\right]}{\Delta \text{t}}=-\frac{\Delta \left[{\text{W}}_{\text{i},\text{j}}\right]}{\Delta \text{t}}\frac{\Delta \left[{\text{W}}_{\text{i},\text{j}}\right]}{\Delta \text{t}}=-{(\frac{\Delta \left[{\text{W}}_{\text{i},\text{j}}\right]}{\Delta \text{t}})}^2\le 0$                          (26)

2. Consequently, Newtonian-like dynamics follows:

$\frac{\Delta \left[W_{i,j}\right]}{\Delta t}=-\frac{\Delta {\text{H}}_{brain}}{\Delta \left[W_{i,j}\right]}$                                                                                                         (27)

3. Independently, Hebb observation of the fact of wired together and fired together

$\frac{\Delta \left[W_{i,j}\right]}{\Delta t}\equiv -\frac{\Delta {\text{H}}_{brain}}{\Delta \left[W_{i,j}\right]}=\left(-\frac{\Delta {\text{H}}_{brain}}{\Delta {\stackrel{\rightharpoonup }{dendrite}}_j}\right)\frac{\Delta {\stackrel{\rightharpoonup }{dendrite}}_j}{\Delta \left[W_{i,j}\right]}\equiv {\stackrel{\rightharpoonup }{g}}_j{\stackrel{\rightharpoonup }{s}}_i$                                                          (28)

Defined: ${\stackrel{\rightharpoonup }{dendrite}}_j\equiv {\sum }_i\left[{\text{W}}_{\text{i},\text{j}}\right]{\stackrel{\rightharpoonup }{S}}_i$ .                                 ${\stackrel{\rightharpoonup }{net}}_j={\sum }_i\left[{\text{W}}_{\text{i},\text{j}}\right]$

Consequently, ${\stackrel{\rightharpoonup }{net}}_j={\sum }_i\left[{\text{W}}_{\text{i},\text{j}}\right]{\stackrel{\rightharpoonup }{S}}_i$ ;                                          ${\stackrel{\rightharpoonup }{\delta }}_j=\left(-\frac{\Delta \text{LMS}}{\Delta {\stackrel{\rightharpoonup }{net}}_j}\right)$

Given the single layer neural network weight matrix learning respectively in either BNN or ANN:

$\Delta \left[W_{i,j}\right]=\left[W_{i,j}\left(t+1\right)\right]-\left[W_{i,j}\left(t\right)\right]=\left\{\begin{array}{l}{\stackrel{\rightharpoonup }{g}}_i{\stackrel{\rightharpoonup }{S}}_i\Delta t\\ {\stackrel{\rightharpoonup }{\delta }}_j\stackrel{\rightharpoonup }{S}{}_i\Delta t\end{array}\right\}$ ;                                                          (29)

We derived a multiple layer Deep Learning BNN

$g_j\equiv -\frac{\partial {\text{H}}_{brain}}{\partial dendrit{e}_j}=-\frac{\partial {\text{H}}_{brain}}{\partial S_j}\frac{\partial S_j}{\partial dendrit{e}_j}=-\frac{\partial {\text{H}}_{brain}}{\partial S_j}{\sigma }_j^{(\text{'})}\left(dendrit{e}_j\right)$  where
(30)

$-\frac{\partial {\text{H}}_{brain}}{\partial S_j}=-{\sum }_k\frac{\partial {\text{H}}_{brain}}{\partial dendrit{e}_k}\frac{\partial dendrit{e}_k}{\partial S_j}{\sum }_k-\frac{\partial {\text{H}}_{brain}}{\partial dendrit{e}_k}\frac{\partial }{\partial S_j}{\sum }_i\left[W_{k,i}\right]S_i={\sum }_k{\tilde{g}}_k\left[W_{k,j}\right]$

$g_j={\sigma }_j^{(\text{'})}\left(dendrit{e}_j\right){\sum }_k{\tilde{g}}_k\left[W_{k,j}\right]$

Both supervised deep learning (SDL) or Unsupervised Deep Learning (UDL) are self-similarly derived within the derivative of the sigmoid window function${\sigma }_j^{(\text{'})}\left(dendrit{e}_j\right);{\sigma }_j^{(\text{'})}\left(ne{t}_j\right)$ :$\text{O}\left(\Delta \text{t}\right)=\text{η}$ in terms of the backward error propagation algorithms are isomorphic:

$\begin{array}{l}\left[W_{ji}\left(t+1\right)\right]-\left[W_{ji}\left(t\right)\right]=\\ \left\{\begin{array}{c}\eta {\stackrel{\rightharpoonup }{S}}_i{\sigma }_j\left(dendrit{e}_j\right)\left\{1-{\sigma }_j\left(dendrite\right)\right\}{\sum }_k{\tilde{g}}_k\left[W_{k,j}\right]+{\alpha }_{momtum}\left[W_{ji}\left(t\right)-\left[W_{ji}\left(t-1\right)\right]\right]\\ \eta {\stackrel{\rightharpoonup }{S}}_i{\sigma }_j\left(ne{t}_j\right)\left\{1-{\sigma }_j\left(ne{t}_j\right)\right\}{\sum }_k{\tilde{\delta }}_k\left[W_{k,j}\right]+{\alpha }_{momtum}\left[W_{ji}\left(t\right)-\left[W_{ji}\left(t-1\right)\right]\right]\end{array}\right\}\end{array}$
(31)
To avoid local minimum of energy landscape, the momentum term ${\alpha }_{momtum}$ has been suggested by R. Lipmann 1987.

Human brain weighs about 3 pounds, made of the Gray matter, neurons, and White matter made of fatty acids Glial cells. Our brain consumes 20% of our whole body energy. As a result, there are many pounds of biological energy by-products, e.g. beta Amyloids, etc. In our brain, Billions Astrocytes Glial Cells are silent partners servant cells to Billions Neurons are responsible to clean dead cells and energy production ruminants from those narrow corridors called Brain Blood Barriers as the Glymphatic system. This phenomenon has been reviewed recently by M. Nedergaad & S.¹ Goldman (“Brain Drain Sci. Am. March 2016”). (Figure 25) They have discovered a good quality sleep about 8 hours, or else, the professionals & seniors with sleep deficient will suffer the slow death dementia, e.g. Alzheimer (blockage at LTM at Hippocampus or STM at Frontal Lobe) Parkinson (blockage at Motor Control Cerebellum) (Figure 26-28) (Figure 28).^2-11

BDA on drug discover

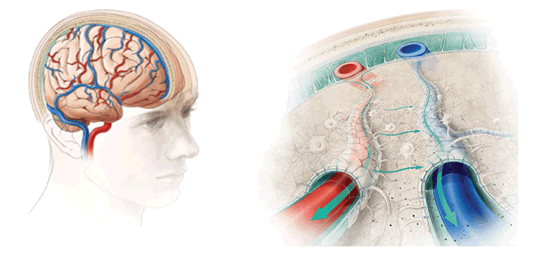
Figure 25 Brain Drain M. Nedergaad & S. Goldman, Sci. Am. March 2016” 100B Astrocytes glials work day and night to clean out the energy production junks such as Omega Amyloid in order to keep up 20% energy usage of the whole human body.

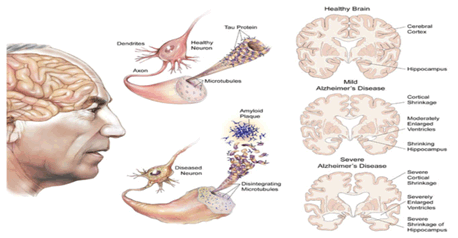
Figure 26 New York Times (Pam Belluck, Nov 23 2016) An experimental Alzheimer’s drug that had previously appeared to show promise in slowing the deterioration of thinking and memory has failed in a large Eli Lilly clinical trial, dealing a significant disappointment to patients hoping for a treatment that would alleviate their symptoms. The failure of the drug, solanezumab, underscores the difficulty of treating people who show even mild dementia, and supports the idea that by that time, the damage in their brains may already be too extensive. And because the drug attacked the Amyloid plaques that are the hallmark of Alzheimer’s, the trial results renew questions about a leading theory of the disease, which contends that it is largely caused by Amyloid buildup.

Figure 27 Astrocytes are closely related to blood vessels and synapses. In fact, they have processes that are in direct contact with both blood vessels and synapses. This makes them ideal candidates for neurovascular regulation. In 2003, an increase in the amount of intracellular Ca2+ in astrocytic endfeet was discovered upon electrical stimulation of neuronal processes. The increase led to dilatation of local cerebral arterioles, successfully linking astrocytes with a role in neurovascular regulation. But an increase in astrocytic Ca2+ is not only mobilized by neuronal activation. A number of transmitters, neuromodulators and hormones can in fact do the exact same thing, independently of synaptic transmission in neurons. Therefore, astrocytes also regulate the response of the cerebral vasculature. Further still, studies have shown that astrocytes could also account for a significant portion of energy consumption in the brain (see references 2 and 3). Although, neurons obtain most of their energy by glycolysis, astrocytes derive much energy from oxidative metabolism and the associated release of glial transmitters, such as ATP, duringCa2+ signaling Khalil A. Cassimally July 17, 2011. Are fMRI Telling The Truth? Role of Astrocytes In Cerebral Blood Flow Regulation.

Figure 28

1. 2000 Literature Nobel Laureate China Mr Gao Xingjian recovered from cancer
2. NIH/CAM: Herbal Medicine G Lucidum, Lingzhi
3. Merck Keytruda (Pembrolizumab)
4. (d)Jimmy Carter Liver and brain Metastasis advanced Melanoma Aug. 2015 ~Feb. 2016.

Our definition of Glial cells seems to be correct, since the Brain Tumor Glioma the denominator of dendrite sum which has a potential singularity by division of zero. if MFE of brain is not correspondingly reduced. This singularity turns out to be pathological in consistent with the medically known brain tumor “Glioma.”  Majority brain tumors belong to this class of too strong glue force. Notably the former President Jimmy Carter suffered from Glioma of three golf-ball size large tumors. Nevertheless, the immunotherapeutic treatment using the newly marketed Phase-4 monoclonal antibody presenter drug (Protocol: 2 mg per kg body weight IV injection) that ID malign cells and tag them for Anti-body swallow malignant cells made by Merck Inc. (NJ, USA) as Anti-Programming Death Drug-1 Keytruda (Pembrolizumab). Mr. Carter was recovered in 3 weeks but took 6 month recuperated (Aug. 2015-Feb 2016) implicated a 4P medicine: personalized, precision, preventive & preemptive drug.

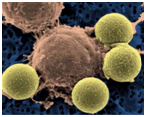
Furthermore, BDA is divided into open sets of Large Data Analysis (LDA) defined as the relational data basis (Attribute, Object, Value) = (Color, Apple/McIntosh, Red Delicious/Green Tarnish) or the other homogeneous data structure (SS#, Name, Sex, Age, Profession, etc.). Some of them may require a NI effortless decision-making known as Unsupervised Deep Learning (UDL) given; therefore, we have developed from thermodynamics for the first time as follows. Is the Herbal Mushroom G Lucidum, Lingzhi (that 2000 Nobel Laureate Literature Mr. Gao Xingjian recovered in cancer) similar to Merck immunotherapy Keytruda (Pembrolizumab) drug (that President Jimmy Carter Liver and Brain Metastasis cancer: Aug. 2015 ~Feb. 2016)? While Merck drug (Yellow balls) are targeted at the Programmed cell Death 1 (PD-1) receptor and allows the body's own immune system go after the cancer cells. While they are all worked on human immune systems, the key difference between Oriental Herbal Medicine and Western Molecular personalized precision targeted drug is in that the holistic is slow in nature of herbal drug for years versus drug in half year.
The biomedical industry can apply ANN & SDL to these kinds of profitable BDA, namely Data Mining (DM) in Drug Discovery, e.g. Merck Anti-Programming Death for Cancer Typing beyond the current protocol (2mg/kg of BW with IV injection), as well as NIH Human Genome Program, or EU Human Epi-genome Program BDA Drug Discovery: FDA Application of Explainable Computational Intelligence to: Explainable A: One can help DARPA (I2O) during PPI applied the Supervised Deep. Learning Classifier vs. Unsupervised Deep Learning for Ortho-Normal Salient Feature Extraction

We have reviewed our unified theory of all six types Neuroglia cells. This might be "déjà vu" to the days when Warren McCullouch & Walter Pitts 1943 and John Von Neumann has defined binary neuron. Although AI ANN & NI BNN have equivalent algorithm, the identification can help engineers and biologists to fuse both sides of knowledge to make the advancements. Since the Homeostasis theory of symbiotic survival by rejuvenating neurons and neuroglia can be mathematically identified in aforementioned summary Eq(19)-Eq(24), the root course of disorder might be remediated via induced pluripotent Stem cells treatments. Consequently, the importance of early diagnostic through brain imaging in terms of isothermal Helmholtz Minimum Free Energy (MFE) could be implicated to more innovative studies. Besides Google Cloud Computing has democratized BDA as AI Deep Machine Learning (e.g. Dr. Fei-Fei Li, Stanford AI Lab & Goggle; TED, ExpovistaTV), some small scale apps are given herewith:

What is the Cost Functions for supervised and unsupervised DL? Supervised DL utilizes the LMS errors for Artificial Intelligence (AI), ANN learnable relational databases; Unsupervised DL utilizes the Minimum Free Energy (MFE) at BNN at Helmholtz MFE for Natural Intelligence (NI), if and only if (i) Isothermal Brain (ii) Power of Pairs Machine Vision for multiple layer Convolution Neural Networks (as if were piecewise nonlinear space-variant p.s.f.) (Table 2).

Table 2 N=57; Epidemiological distribution of the pathological fractures, traumatic fractures, and nonunion

Defense& Homeland Security Applications: Augmented Reality (AR) & Virtual Reality (VR)

Just like chess games, the law & order societal affairs, e.g. flaw in banking stock markets, and Law Enforcement Agencies, Police and Military Forces, who may someday require the "chess playing proactive anticipation intelligence" to thaw the perpetrators or to spot the adversary in a "See-No-See" Simulation & Modeling, at the man-made situation, e.g. inside-traitors; or in natural environments, e.g. Weather and turbulence conditions. In conclusion, we should enhance the eroded superiority of hardware's with smart software's: SDL & ANNs and/or UDL & BNN through daily Training & Documentation, e.g. matching day intruder pictures with night perpetrator pictures at the persistent surveillance critical perimeter similar to proactive chess game playing in a limited size about a football field. There remains to gain the trustworthiness by DARPA Explainable AI (XAI) (Figure 29).

Figure 29 Example of ANN applications in modeling & simulation, including real time software defined multispectral cameras to see through dusts by LWIR, and fires by SWIR.

None.

Author declares that there is no conflict of interest.

1. Nedergaad M, Goldman S. Brain Drain. Sci Am. 2016;314(3):44‒49.
2. Shinya Yamanaka Nobel Prize in Medicine & Physiology has been given in 2012 to the discovery genes by Kyoto, and these 4 Yamanaka genes can be unwind cells back to the embryonic (adult cells induced pluripotent: mice, Dolly Sheep, Homosapiens longevity)
3. Common Sense Longevity: Sleep Tight, Eat Right (NIH/NIA Dir. Matterson. Calorie Restriction: Prof. Luigi Fontana Alternative Fasting, Wash U.), Deep Exercise (e.g. Tai Chi Quan), Be Happy (Vegas).
4. Nicola J. Learning Machine. Nature. 2014;505(7482):146‒148.
5. LeCun Y, Bengio Y, Hinton G. Deep Learning. Nature. 2015;521(7553):436‒444.
6.  Harold Szu. Natural Intelligence Neuromorphic Engineering. Elsevier; 2017. p. 1‒350.
7. Harold Szu, Henry Chu, Simon Foo. Deep Learning ANN & Apps. USA: Elsevier Book Publisher; 2017. p. 16‒18.
8. Harold S, Lidan M, Hairong Q. Unsupervised Learning at MFE (single layer LCNN for one class breast cancer or not), appeared in Proc. 6576. 2007. p. 605‒657.
9. Paul Werbos. Multiple Layer Deep Learning appeared in Introduction to Computing with Neural Nets Richard Lipmann. In: IEEE ASSP Magazine, PDP Book, MIT 1986 book (James McCelland, David Rumelhart) PDP group, USA; 1987.
10. Newman EA. New roles for astrocytes: Regulation of Synaptic transmission. Trends in Neuroscience. 2003;26(10):536‒42.
11. Fields RD, Steven-Graham B. New Insights into Neuron-Glia Communication. Science. 2002;298(5593):556‒62.

Dr. Harold (Hwa-Ling) Szu has been a champion of Unsupervised Deep Learning Computational brain-style Natural Intelligence for 3 decades. He received the INNS D. Gabor Award in 1997 “for outstanding contribution to neural network applications in information sciences.  He pioneered the implementations of fast simulated annealing search.  He received the Eduardo R. Caianiello Award in 1999 from the Italy Academy for “elucidating and implementing a chaotic neural net as a dynamic realization for fuzzy logic membership function. Dr. Szu is a foreign academician of Russian Academy of Nonlinear Sciences for his interdisciplinary Physicist-Physiology to Learning (#135, Jan 15, 1999, St. Petersburg).  He is a Fellow of American. Institute Medicine & Bioengineering 2004 for passive spectrogram diagnoses of cancers; Fellow of IEEE (#1075,1997) for bi-sensor fusion; Fellow of Optical Society America (1995) for adaptive wavelet; Fellow of International Optical Engineering (SPIE since 1994) for neural nets; Fellow of INNS (2010) for a founding secretary and treasurer and former president of INNS.   Dr Szu has graduated from the Rockefeller University 1971, as thesis student of G. E. Uhlenbeck. He became a visiting member of Institute of Advanced Studies Princeton NJ, as well as a civil servant at NRL, NSWC, ONR, and then a senior scientist at Army Night Vision Electronic Sensory Directorate, Ft. Belvoir VA over 40 years. To pay back the community, he served as research professor at AMU, GWU, and CUA, in Wash DC. Besides 640 publications, over dozen US patents, numerous books & journals (cf. researchgate.net/ profile/Harold_Szu2). Dr. Szu taught thesis students “lesson in creativity: editorial” (for individual with 4C principles and for a group by 10 rules) following a Royal Dutch tradition from Boltzmann, Ehrenfest, & Uhlenbeck (Appl. Opt. 54 Aug. 10, 2015). He has guided over 17 PhD thesis students

 Michael J. Wardlaw was born in Greensboro N.C. in 1960 and obtained a BSEE focusing on electromagnetics and antenna theory in 1983 from North Carolina A&T State University (NCA&TSU) in Greensboro, NC later obtaining a MSEE with a thesis in optical signal processing in 1992 from North Carolina State University (NCSU) in Raleigh, NC.  He has held several leadership positions over 35+ years working for the Department of Navy, most of which at the Naval Surface Warfare Center (NSWC) in Dahlgren, VA. During his tenure there, he was Lead Engineer on numerous passive and active photonic sensor R&D efforts. While a graduate student at NCSU under Anthony “Bud” VanderLugt (1990-1992), his interest expanded to incorporate optical signal processing and information theory. He subsequently became Leader of the Advanced Systems Concepts Group at NSWC and significantly increased the Navy’s activity in optical signal processing; laser based sensor technologies and high-energy laser weapons. Leveraging this experience, he developed the Navy’s High Energy Laser (HEL) Roadmap, resulting in the reestablishment of a US Navy Directed Energy (DE) thrust into laser-based weaponry. Between 1998 - 2003 Mr. Wardlaw was Director of Laser Technology and Advanced Systems Concepts for NSWC, leading several laser development programs. Currently, he is leads the Maritime Sensing Group at the Office of Naval Research located in Arlington, VA. He and his team are responsible for funding and executing ONR S&T research and development in acoustic and non-acoustic sensing technologies applicable to anti-submarine warfare (ASW) and mine warfare (MIW) applications. He explicitly executes a Discovery and Invention portfolio that develops advanced photonic technologies; laser based systems and associated advanced computing technologies. Finally, Mr. Wardlaw leads some of ONR’s most revolutionary projects such as the Surface Ship Periscope Detection and Discrimination (SSPDD) Future Naval Concept (FNC) and the Forward Deployed Energy and Communications Outpost (FDECO) Innovative Naval Prototype (INP). These major ONR projects bring together innovations from across the entire government and commercial S&T community.  Mr. Wardlaw has received numerous Navy citations and awards in addition to being selected as year 2000 Black Engineer of the Year for Outstanding Technical Contribution in Government. He holds several patents and has been active in the Directed Energy Professional Society (DEPS), the Association of Old Crows (AOC), the Institute of Electrical & Electronics Engineers (IEEE), the American Association for the Advancement of Science (AAAS), the Optical Society of America (OSA) and the Society of Photographic Instrumentation Engineers (SPIE).

Dr. Jeff Willey, is the director of research at RFNav Inc.  He received his BS in Biology from RPI, an MSEE from the University of Connecticut, and a DSc in EE from George Washington University in 2001.  Mr. Willey contributed to the research, development, and analysis of novel radar systems and other sensing systems at the US Naval Research Laboratory (NRL) starting in 1981 and later at the Johns Hopkins University Applied Physics Laboratory.  His patents cover radar, imaging, and RF based speech recognition.  His research interests include RF sensors for autonomous vehicles, non-invasive sensing systems, and learning and error prediction in neural network classifiers.

Dr. Charles Hsu is the senior scientist, and he dedicated more than 20 years on the research and development in the defense science, technology and engineering for systems developments and software engineering (SE).  His works and achievement may be highlighted with selected more than 200+ publications on all aspects of mathematical wavelets analysis, Independent Component Analysis (ICA), image/video analyses, military operations and applications for detections, recognitions and identifications (DRI), video surveillance algorithmic developments, SAR/GMTI radar detection, exploiting GMTI data and SAR imagery in a multi-INT fusion environment with exposure and use of multiple intelligence analysis sources, and etc.  Dr. Hsu was a major Co-Investigator (CI) of the video over radio lossless transmission project named WaveNet sponsored by Army CECOM a decade ago.  He continued his compression expertise into the RF components domains under DoD sponsorship on moving platforms, e.g. Special Operations Craft Riverine (SOC-R) FOPEN SAR by SOCOM and Tier-I Unmanned Air Vehicles (UAV) Silver Fox by ONR.  In addition, he obtained a direct funding from Home Land Security Agency (DHS) as a trusted PI on the persistent surveillance against human intruders using a smart distant sensors suite with build-in self-healing reconfigurable surveillance EOIR camera sensors nodes, triggered in action by ground infrared sensors. Recently, his research and work are focused on the GMTI collection systems, data acquisition, processing, exploitation, and production.  His working experience may be summarized as a result- oriented researcher, abided the requirements of specification, executed with the integration performance T&E, and finished with quality control and on-time project delivery management.

Kim Scheff lives in College Park Maryland.  He received his BA, Physics and Math, from the University of Minnesota, ‘79 and MA, Physics, SUNY @ Buffalo ‘85.  He spent several years doing neural network research at Clark University before going to industry first in neural networks and for the past 20+ years performing radar research and development.  One of his research radars uses wavelets as radar waveforms for high range resolution applications.

Simon Y. Foo, Ph.D., is a tenured Professor at the Department of Electrical and Computer Engineering (ECE) at Florida A&M University and Florida State University. He is currently the ECE department Chair. His research contributions have been in the areas of computational intelligence especially neural networks, genetic algorithms, and fuzzy logic. He is also active in research on photovoltaics, particularly high-efficiency multi-junction III-V compound solar cells and perovskite-based polymer solar cells. Dr. Foo has authored or co-authored over 100 refereed technical papers, was awarded a patent on high efficiency multi-junction solar cells, and contributed to two book chapters. He has also graduated more than 30 MS and PhD students. He is the Principal Investigator of at least 20 funded research projects with total funding of over 3 million dollars. His primary research sponsors include the National Security Agency, National Science Foundation, U. S. Air Force, Boeing Aircraft Company, and the Florida Department of Transportation. He also serves as a technical advisor to Airbus in the area of fire detection in aircraft cargo bays. He has won several awards such as the "Engineering Research Awards" from the FAMU-FSU College of Engineering, Tau Beta Pi Teacher of the Year award, and "Best Paper" awards. He is a member of Eta Kappa Nu Electrical Engineering Honor Society.

Dr. Chee-hung Henry Chu is the Executive Director of the Informatics Research Institute (IRI) and Professor in the School of Computing and Informatics at the University of Louisiana at Lafayette. His research interests are in machine learning and machine vision. He has worked extensively in recovering perspective transform as well as planar homography from images. At IRI, he oversees research and development programs in data science and big data analytics, health informatics, emergency management and disaster recovery, and smart communities. These projects are conducted in collaboration with the Louisiana Department of Health, Louisiana Office of Governor’s Homeland Security and Emergency Preparedness, the National Science Foundation, US Ignite, as well as other industrial partners.  Chu received his B.S.E. and M.S.E. degrees from the University of Michigan and a Ph.D. degree from Purdue University. He is a Registered Professional Engineer, a senior member of the IEEE, and a member of the honor societies of Eta Kappa Nu, Tau Beta Pi, and Phi Kappa Phi.

  Mr. Joseph Landa is a founding partners in Briartek Incorporated a Virginia Company that designs, manufactures and sells advanced safety products to help locate people who want to be found.   During the undergraduate and graduate studies, he joined ROTC in order to study the Physics at Clark University and continued, with Prof. Harold Szu, at The American University.  When the Desert Storm came, he studies has to be interrupted and served the Country as an Army combat engineering officer. During his shipping over the sea, he realized how many fallen soldiers could not push the button for the traditional over board alarming system. He has been honorably retired as Army Captain. When he came back, the university has terminated their Ph. D. program in Physics. He moved on to design the automatic man overboard alarm system, and has successfully passed the Navy and the Coast Guard test as the only safety item listed in GSA schedule. The device has further passed the US Export Control to sale to the Great Brain Navy. Mr. Landa holds numerous patents and remains active in various research and standards development communities, as well as he serves the local community services. He has proved BriarTek as one of the most successful and innovative businesses, due to Joe's leadership as a creative and ingenues working engineer.

Yufeng Zheng received his Ph.D. degree in Optical Engineering/ Image Processing from Tianjin University in 1997. He is presently with Alcorn State University (Mississippi, USA) as an associate professor (tenured). Dr. Zheng serves as a program director of the Computer Network and Information Technology major, as well as the director of Pattern Recognition and Image Analysis Lab. He is the principle investigator on four federal research grants in night vision enhancement, thermal face recognition, and multispectral face recognition. Dr. Zheng holds two patents on glaucoma classification and face recognition, and has published three books, six book chapters, and more than 70 peer-reviewed papers. His research interests include biomedical imaging, facial recognition, information fusion, night vision colorization, bio-inspired image analysis, and computer-aided diagnosis. Dr. Zheng is a Cisco Certified Network Professional (CCNP), a senior member of SPIE, and a member of IEEE & Signal Processing Society.

Jerry Wu received the PhD in Electrical and Computer Engineering from the George Washington University in 2008. He is currently the adjunct faculty at the University of Maryland, College Park. His research interests include VLSI circuit design with low power, FPGA/DSP and hardware/software co-design, embedded systems, Satellite communication, MEMS technologies and application to mobile device RF design, biomedical sensors, and brainwaves EEG. He is currently working at J2 Universe LLC.

Eric Wu is a current Computer Science major at the University of Maryland. In the past, he has worked alongside researchers and scientists at the Army Research Laboratory to conduct research on solar powered and fuel cell vehicles. He has also worked at NIST to research Crystal Lattice structures and the application of density matrices and polarization functions from crystal structures. He is tailoring his studies at the University of Maryland and any future studies towards topics surrounding Cyber-Security and Artificial Intelligence.

Hong Yu graduated from University of Hunan and received his Master degree and Ph.D. degree from the Department of Electrical Engineering and Computer Science of The Catholic University of America, USA in 2008. Currently, he is a full professor of Electrical Engineering and Computer Engineering at Capitol Technology University. His teaching and research areas include network protocol, embedded system design, FPGA, VLSI design, optical switching application, renewable energy development and deep learning Neural Network.  He is senior membership of IEEE and membership of ASEE.

Guna Seetharaman is the Navy Senior Scientist (ST) for Advanced Computing Concepts, and the Chief Scientist for Computation, Center for Computational Science, Navy Research Lab.  He leads a team effort on: Video Analytics, High performance computing, low–latency, high-throughput, on-demand scalable geo-dispersed computer-networks.  He joined NRL in June 2015. He worked as Principal Engineer at the Air Force Research Laboratory, Information Directorate, where he led research and development in Video Exploitation, Wide Area Motion Imagery, Computing Architectures and Cyber Security.  He holds three US Patents, and has filed more disclosures, in related areas. His team won the best algorithm award at IEEE CVPR-2014 Video Change Detection challenge, featuring a semantic segmentation of dynamic scene to detect change in the midst of dynamic clutters. He served as a tenured professor at the Air Force Institute of Technology, and University of Louisiana at Lafayette, before joining AFRL. He and his colleagues cofounded Team Cajubbot and successfully fielded two unmanned vehicles at the DARPA Grand Challenges 2004, 2005 and 2007.  He also co-edited a special issue of IEEE Computer dedicated to Unmanned Vehicles, and special issue of The European Journal Embedded Systems focused on intelligent autonomous vehicles.  He was elected as Fellow of the IEEE, in 2014, for his contributions in high performance computer vision algorithms for airborne applications.  He also served as the elected Chair of the IEEE Mohawk Valley Section, Region 1, FY 2013 and FY 2014.

Jae H. Cha is an Electronics Engineer with the Night Vision and Electronics Sensors Directorate. He received his M.S. Degree from Virginia Tech, and a B.S. degree from George Mason University. His research interests include IR sensor modeling and simulation, image processing, and computer vision. He is a Ph. D. Candidate at ESE Dept, VPI & SU, Blacksburg VA.