Traumatic spinal injuries pose a significant medico-social challenge, with about 60% of all spine fractures occurring at the thoracolumbar junction. Optimizing care for these patients remains a critical issue, despite the development of numerous surgical and conservative treatment methods, with outcomes still far from ideal. A key factor contributing to the consistently high rate of unsuccessful surgical interventions, which lead to stabilization failures in both the early and late postoperative periods, is the disregard of the biomechanical characteristics of the thoracolumbar junction area. Clinical protocols often regulate intervention methods based on the degree and nature of damage to the thoracolumbar spine as a whole. Enhancing the reliability of fixation, while maintaining the number of transpedicular screws, can be significantly achieved by using cross-links and adjusting screw length. The purpose of our study was to investigate the distribution of loads on the metal construct elements and bone structures in the thoracolumbar junction after extensive decompressive-stabilizing interventions. The load was modeled with a backward tilt. A mathematical finite element model of the human thoracolumbar spine segment was developed, incorporating vertebrae Th9-Th11, L2-L5, with Th12-L1 vertebrae removed, as well as elements of the metal construct—interbody support and a transpedicular system. We modeled four variants of transpedicular fixation using both short and long screws that penetrate the anterior surface of the vertebral body, with and without the use of two cross-links. Stress parameters were monitored at 20 control points in the models. Comparative analysis of the results revealed that models including long bicortical screws and two cross-links demonstrated the best biomechanical performance when the torso was tilted backward, effectively reducing stress in critical areas and enhancing the durability and effectiveness of the fixation.

Keywords: thoracolumbar junction, spinal trauma, biomechanics, corpectomy, finite element analysis, spinal stabilization

Traumatic spinal injuries represent a significant medical and social issue within modern society, characterized by a high rate of disability among the workforce and substantial financial burdens associated with both immediate healthcare provision and long-term maintenance of victims’ quality of life through sustained rehabilitation efforts.¹ Ongoing research to improve the efficacy of existing therapeutic modalities and develop innovative treatment strategies for spinal trauma remains a critical priority. Despite significant progress in this domain, the therapeutic outcomes for affected individuals are still suboptimal.²

Injuries to the thoracolumbar junction (TLJ), which includes the two lower thoracic and two upper lumbar vertebrae, constitute approximately 60% of all spinal trauma cases, as evidenced by various studies.^3,4 This prevalence is attributed to the biomechanical properties of this spinal region. The transition from the high rigidity of the thoracic spine, with facet joints oriented in the coronal plane and relatively small intervertebral discs, to the highly mobile lumbar spine, featuring sagittal facet orientation and larger intervertebral discs, makes the TLJ particularly susceptible to injury.⁵ This area, notably lacking physiological curvature, thus faces limited shock-absorbing capabilities, rendering it exceptionally prone to trauma.⁶

Evidence-based medicine is the foundational principle of contemporary medical practice, necessitating theoretical rationale and clinical validation for the selection of treatment methodologies, especially for patients with traumatic spinal injuries. The AOSpine Thoracolumbar Traumatic Injury Classification System serves as a predominant framework guiding the differentiated strategy and tactics in therapy.⁷ This classification has been instrumental in developing numerous methodological guidelines and clinical protocols for treating such injuries.^8–10 However, a significant concern is the lack of consideration for the specific biomechanics of the TLJ in surgical method selection, as the classification broadly encompasses the entire thoracic and lumbar regions.¹¹

This has led to a notable body of literature indicating the inadequacy of short fixation, and the potential for fragmentation or dislocation within stabilization systems, particularly at the TLJ.^12,13

This article is extracted from a broader study dedicated to the biomechanics of the operated thoracolumbar junction.^14–16 It posits that the surgical approach to spinal trauma, particularly at the TLJ, must be rigorously determined by the extent and nature of the osteo-ligamentous alterations incurred through injury.¹⁷ The study analyses a model for massive structural damage, necessitating vertebral resection and subsequent stabilization to restore spinal alignment and functionality.

Such circumstances undoubtedly impose increased demands on stabilization, which must ensure not only reliable and rigid fixation but also facilitate the maximum uniform distribution of load across all elements, both metallic structures and bone tissue, to prevent the failure of fixation in the long-term perspective.

The aim of this study was to investigate the impact of the length of the transpedicular screw and the presence of cross-links on the load distribution characteristics during surgical resection of two adjacent vertebrae in the thoracolumbar junction area. The load pattern was simulated based on the patient's vertical position with a backward lean.

Biomechanical investigations into the effectiveness of different stabilization techniques require detailed insights into stress distribution and deformation across a range of structures, encompassing both osseous and metallic components. Consequently, finite element analysis (FEA) emerged as the method of choice due to its precision in simulating complex biomechanical behaviors. At the biomechanics laboratory of the Sytenko Institute of Spine and Joint Pathology of the National Academy of Medical Sciences of Ukraine, a sophisticated finite element model of the human thoracolumbar spine segment was developed. This model specifically included the vertebrae from Th9 to Th11 and L2 to L5, while the Th12 to L1 vertebrae were intentionally omitted to simulate the surgical scenario under study. Additionally, the model integrated components of the metal hardware used in spinal stabilization, featuring an interbody support and a transpedicular system. The structural details and assembly of these elements were meticulously represented to ensure accurate biomechanical analysis. The graphical representation of this model is depicted in Figure 1, illustrating the configuration and components of the thoracolumbar spine segment as rendered in the finite element environment.

As a clinical example, we present the X-ray results of patient M, a 42-year-old male who suffered from a road traffic accident. Figure 1a shows a fracture-dislocation at Th12-L1 with significant destruction of both vertebral bodies. Figure 1b illustrates the results of the surgical intervention - resection of the Th12 and L1 vertebral bodies with restoration of the spinal support function using a vertebral replacement implant, realignment of the spinal axis, and stabilization using a transpedicular stabilizing system with 8 screws (“long” fixation).

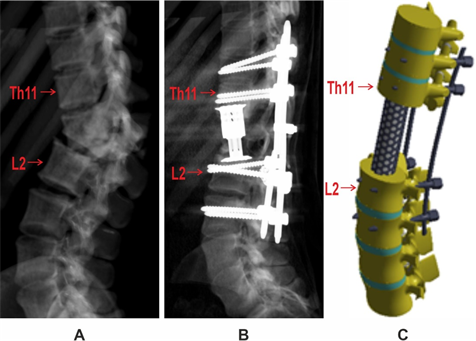
Figure 1 A - Preoperative radiography of patient M, B - Postoperative radiography following decompressive-stabilization surgery, C - External appearance of the finite element model.

During the study, four variants of transpedicular fixation were modeled, using both short fixing screws and long screws that penetrate the anterior surface of the vertebral body, as well as with and without the use of two transverse cross-links.

The choice of finite element (FE) type for mesh construction is well covered in the literature. For instance, K. Polgar and colleagues demonstrate the performance characteristics of tetrahedral finite elements with linear and quadratic approximation functions, which were used to create a mesh for the human femur in conjunction with automatic mesh generation methods.¹⁸ Ten-node quadratic tetrahedra were compared with four-node linear tetrahedral elements in terms of accuracy and central processing unit (CPU) time. Based on this and similar studies, the ten-node tetrahedral element with quadratic approximation was selected as the finite element.

There are also numerous studies dedicated to investigating the convergence of the solution as the size of the finite elements changes. For example, research by Michael A. K. Liebschner and colleagues explored the solution convergence when increasing the FE mesh with quadratic approximation.¹⁹ It was shown that using more than 1700 FEs for the vertebral body resulted in an error of less than 0.5%. Our model consists of 35,161 tetrahedral 10-node isoparametric finite elements with quadratic approximation and has 92,958 nodes, thus more than 3000 FEs are allocated per model of a vertebral body.

It is worth noting that in modern software suites, the size of the element, as well as the number and type of elements, are often automatically determined by the finite element generation program. Such FE mesh generators use various adaptive algorithms that allow building a mesh taking into account the curvature of the surface (different sizes of FEs) and best representing its geometry, smoothing algorithms, and avoiding the creation of elements of unsatisfactory shape.

A static type of load was applied. During the modeling, it was assumed that the material is homogeneous and isotropic, which conforms to the generally accepted principles of finite element analysis in studies similar to ours.²⁰ This approach is sensible as it provides insights into the basic mechanical properties and behavior of biological structures.

The mechanical properties of biological tissues (cortical and cancellous bone, intervertebral discs) for the mathematical modeling were selected based on literature data.^21,22 The material of the prosthetic elements was titanium. The mechanical characteristics of the synthetic materials were chosen according to data from technical manuals.²³ For the analysis, properties such as the Young’s modulus (E) and Poisson's ratio (ν) were utilized. Data on the mechanical characteristics of the materials are presented in Table 1.

This approach facilitated detailed evaluations of the biomechanical performance of various fixation strategies, helping to identify optimal configurations for enhancing spinal stabilization.

The stress-strain state of the models was investigated under the influence of a bending load acting from anterior to posterior, simulating backward tilt of the torso. The load was applied to the body of the Th9 vertebra and the articular surfaces of its spinous processes. The magnitude of the load was 350 N, which corresponds to the weight of the upper part of the body. The distal surface of the L5 disc in the model was rigidly fixed. For effective investigation of changes in the stress-strain state of the models, depending on the method of transpedicular fixation, the following control points were selected for recording stress magnitudes: Vertebral body of Th9 (1), Vertebral body of Th10 (2), Vertebral body of Th11 (3), Vertebral body of L2 (4), Vertebral body of L3 (5), Vertebral body of L4 (6), Vertebral body of L5 (7), Lower endplate of the vertebral body of Th11 (8), Upper endplate of the vertebral body of L2 (9), Entry zone of the transpedicular screw into the arch of Th10 (10), Entry zone into the arch of Th11 (11), Entry zone into the arch of L2 (12), Entry zone into the arch of L3 (13), Screw in the body of Th10 (14), Screw in the body of Th11 (15), Screw in the body of L2 (16), Screw in the body of L3 (17), Transverse ties between Th10 and Th11 (18), Transverse ties between L2 and L3 (19), Vertebral replacement support (20).

The investigation of the stress-strain state of the models was performed using the finite element method. The criterion for evaluating the stressed state of the models was based on von Mises stress.²⁴ The modeling was carried out using the SolidWorks computer-aided design system. Calculations of the stress-strain state of the models were performed using the CosmosM software suite.²⁵

The initial phase of the study focused on analyzing the stress-strain state of the thoracolumbar spine segment model after the resection of vertebrae Th12 to L5 when using transpedicular fixation with short screws without transverse cross-links. The stress distribution within the model is presented in Figure 2.

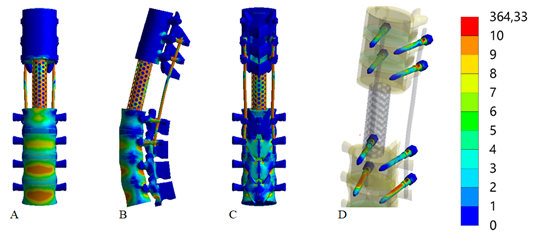
Figure 2 Stress distributions in the model of the thoracolumbar spine segment following the resection of vertebrae Th12-L5 under a backward bending load. The fixation was done using short transpedicular screws without transverse cross-links:
A - Anterior view, B - Lateral view, C - Posterior view, D - Screws.

The conducted studies revealed that when using short screws without transverse cross-links during a backward bending of the torso, the maximum stresses of 14.2 MPa and 13.3 MPa occur in the vertebral bodies of L5 and L4, respectively. High stress levels are also identified at the points of contact between the vertebrae and the interbody support, with 12.7 MPa at vertebra L2 and 11.7 MPa at vertebra Th11. Around the fixing screws, the highest stresses are observed in the lumbar spine vertebrae, specifically 12.4 MPa at L3 and 7.6 MPa at L2. The most stressed screw is located in vertebra L3, with a stress of 39.6 MPa, while stresses in other vertebrae are relatively evenly distributed, ranging from 16.0 MPa to 18.2 MPa. The stress in the interbody support is recorded at 49.2 MPa.

Figure 3 illustrates the stress-strain state of the thoracolumbar spine segment model following the resection of vertebrae Th12-L5 under a backward bending load, using long screws for transpedicular fixation without transverse cross-links.

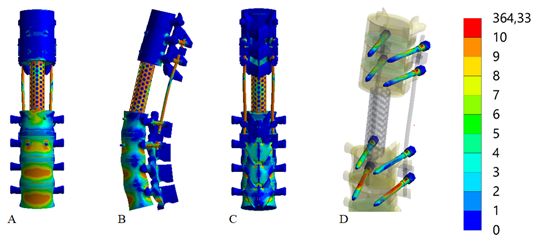
Figure 3 Distribution of stress in the model of the thoracolumbar spine segment after the resection of vertebrae Th12-L1 under the influence of a backward bending load. Transpedicular fixation using long screws without transverse cross-links:
A - Anterior view, B - Lateral view, C - Posterior view, D - Screws.

Replacing the fixation screws with longer ones during a backward tilt of the torso leads to minor changes in the stress levels within the bone structures, generally resulting in a decrease. However, there is a noted increase in stress levels in the metallic structure elements, except for the screws in the L3 vertebra, where the stress magnitude rises to 44.1 MPa. The maximum stresses in the interbody support are identified at 38.7 MPa, and on the screws in the vertebrae L3, Th10, and Th11, the stresses are 12.5 MPa, 15.6 MPa, and 17.8 MPa, respectively.

The distribution of stress in the model of the thoracolumbar spine segment after the resection of vertebrae Th12-L5 under a backward bending load, with transpedicular fixation using short screws and transverse cross-links, can be viewed in Figure 4.

Figure 4 Stress distributions in the model of the thoracolumbar spine segment after the resection of vertebrae Th12-L5 under the influence of a backward bending load. Transpedicular fixation using short screws with transverse cross-links:
A - Anterior view, B - Lateral view, C - Posterior view, D - Screws.

The use of transverse cross-links effectively reduces stress levels at all control points of the model during a backward tilt of the torso. Specifically, the stress levels on the cross-links are measured at 2.7 MPa and 6.9 MPa in the thoracic and lumbar sections, respectively.

The final stage of the study will examine the impact of transverse cross-links when using long fixation screws on the stress distribution in the model during a backward torso tilt (Figure 5).

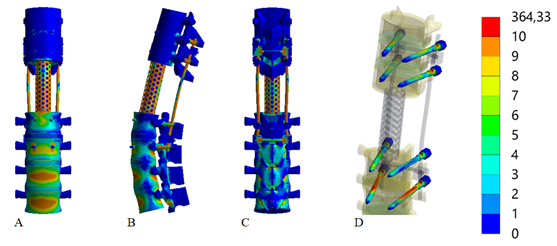
Figure 5 Stress distributions in the model of the thoracolumbar spine segment after the resection of vertebrae Th12-L5 under the influence of a backward bending load. Transpedicular fixation using long screws with transverse cross-links:
A - Anterior view, B - Lateral view, C - Posterior view, D - Screws.

The conducted studies have shown that using long screws in combination with transverse cross-links during a backward torso tilt does not lead to significant changes in the stress-strain state of the model compared to using short screws, except for an increase in stress levels at the screws in the L3 vertebra body to 41.2 MPa. However, compared to the model using long screws without cross-links, the stress levels are reduced at all control points of the model.

Data on the maximum stress values at all control points of the models for all variants of transpedicular fixation are presented in Table 2.

The table presented provides a detailed comparison of stress values across four different models of thoracolumbar spine stabilization under a backward bending load. These models differ in terms of the length of the screws (short vs. long) and the presence or absence of transverse cross-links. Here's a detailed overview and comparison based on the data:

1. Short screws without cross-links:
   1. This model generally shows higher stress values across most vertebral bodies compared to models with cross-links, indicating a lesser distribution and absorption of stress without the additional support.
   2. Particularly high stresses are noted in the lower lumbar region, with the L5 vertebral body experiencing the highest stress at 14.2 MPa.
   3. The stress at the screw entry points also tends to be higher, which could indicate a greater concentration of force around the screw sites, potentially increasing the risk of hardware failure or bone damage over time.
2. Long screws without cross-links:
   1. This setup shows a mixed response in stress reduction compared to short screws without cross-links. For instance, the vertebral body L2 shows a slight decrease in stress (7.6 MPa from 8.4 MPa with short screws), suggesting better stress distribution with longer screws.
   2. However, in some areas such as the L3 vertebral body, the stress is higher (8.6 MPa) compared to the short screws model, possibly due to the increased lever arm effect of longer screws.
3. Short screws with cross-links:
   1. Adding cross-links to short screws significantly reduces stress in most areas, particularly in the higher stress regions of the lumbar vertebrae. For example, stress in the L5 vertebral body decreases from 14.2 MPa to 13.4 MPa.
   2. The reduction is also notable in the thoracic vertebrae, where the inferior vertebral body of Th11 shows a decrease from 11.7 MPa to 10.5 MPa.
   3. The presence of cross-links seems to aid in better distribution of the load across the spine, thus alleviating stress at individual points.
4. Long screws with cross-links:
   1. This model generally offers the best stress distribution among all configurations. It significantly lowers stress in crucial areas such as the vertebral body L2 (from 7.6 MPa to 7.5 MPa) and the superior vertebral body L2 (from 10.3 MPa to 9.6 MPa), despite these reductions being modest.
   2. The stress values around the screws and at the cross-link locations are also among the lowest, indicating a robust stabilization setup that effectively spreads out the load, potentially enhancing the durability and effectiveness of the fixation.

In summary, the addition of cross-links, regardless of the screw length, generally improves stress distribution and reduces peak stress values across the spine model. Long screws with cross-links present the most favorable outcomes in terms of stress management, suggesting their efficacy in clinical settings where spinal stability and reduced risk of mechanical failure are crucial.

Upon reviewing the relevant literature, no studies were found that matched the design of our research, which could either confirm or refute our findings. This scarcity may be attributed to the fact that while traumatic injuries to TLJ are common, instances necessitating the total removal of two adjacent vertebral bodies due to extensive fragmentation are relatively rare. Additionally, many surgeons opt for combined anterior-posterior approaches, which involve different surgical instruments and techniques.^26,27

Our clinical observations affirm that isolated posterior access is capable of comprehensively addressing all surgical challenges associated with traumatic TLJ injuries of any severity.²⁸ These include the decompression of spinal canal structures, correction of the spinal axis - even in cases with significant spondyloptosis, and adequate stabilization.

The effectiveness of using cross-links, as observed in our study, aligns with existing literature that suggests such techniques enhance stabilization.²⁹ This affirmation is crucial given the biomechanical context of our experimental setup. However, the debate over the use of bicortical versus monocortical screws is nuanced.^30,31

Bicortical screws are often preferred in clinical settings for osteoporotic spines because they reduce the stress at the screw-bone interface, thereby lowering the risk of loosening and subsequent stability loss. Our findings support this practice. Conversely, long screws, while providing certain benefits, increase the load on the screws, potentially enhancing metal fatigue and elevating the risk of screw fragmentation. Therefore, the selection of fixation methods should be critically evaluated, weighing the benefits against potential drawbacks.

Further exploration could involve comparing our findings with other models under different loading scenarios, some of which have been previously published. Notably, extension loading—common in active individuals—tends to be more favorable regarding load distribution on the operated thoracolumbar junction even compared to compression loading.¹⁶ This is due to the minimal increase in load on the lower elements of the metal structure and the areas of screw contact with bone tissue. In contrast, flexion loading imposes significantly higher stresses across all elements of the model.¹⁵

The determination of the physico-mechanical properties of bone tissues has been developing along several lines since the middle of the last century. Alongside simplified models, the anisotropy of bone tissue has also been extensively studied.^32–34 These studies continue to this day. It is worth noting that assuming isotropy and homogeneity of the material, researchers obtained various physico-mechanical characteristics of bone tissue, which varied within quite wide limits. For example, the modulus of elasticity for cortical bone varies between 10000 MPa to 22000 MPa in different studies, and for cancellous bone it ranges from 100-200 MPa.^35,36

However, further research has led to physico-mechanical characteristic values that vary within a range of 10-15% (for instance, the Young's modulus for cortical bone in most modern works is cited within the range of 17-20 GPa). In studies on material anisotropy, such progress has not been achieved, with results showing variations up to 50%. Discussions continue regarding the influence of accounting for various models of material physico-mechanical properties on the results of biomechanical model stress-strain calculations.^37,38

At the current stage, attempts to use new approaches are being made to obtain more accurate values of material characteristics. Promising are studies where an anisotropic finite element model is derived from tomographic studies, which moves closer to the possibility of constructing individual models.³⁹ Despite the fact that bone tissue is inherently anisotropic, it should be noted that in the values defining the anisotropy of bone tissue, researchers have not reached a consensus, and currently, the consideration of material anisotropy and its impact on the accuracy of the results remains a matter of debate. Based on the above, the authors considered it possible to use averaged values of the physico-mechanical properties of materials, also presented in the works of other researchers.

Furthermore, it should be noted that recognizing the material as homogeneous and isotropic significantly simplifies mathematical models and computational processes. Biological tissues often possess complex, heterogeneous, and anisotropic properties, making their accurate modeling extremely labor-intensive. Simplifying tissue properties to homogeneous and isotropic allows for more effective calculation of stresses, strains, and other important mechanical parameters.

In constructing the model, the material was assumed to be homogeneous and isotropic. The poroviscoelastic nature of the spinal tissues was omitted by assuming that all the loads were applied under quasi-static loading conditions. Considering the significant individual variability in mechanical and anatomical structures, tailoring the model parameters to a specific patient does not seem appropriate, as the main task of this work was to evaluate stress distribution under various loading patterns with the prospect of further extrapolating the results to the population as a whole. It is for this reason that such a type of simplification appears sensible and justified.

The results obtained in the study do not allow for a definitive conclusion on the appropriateness of using one stabilization method or another in the case of explosive fractures of the thoracolumbar junction. However, further research, specifically the study of all loading patterns, will allow for an assessment of the potential risks and benefits of various surgical techniques.

Using transverse cross-links significantly reduces stress levels at all model control points, regardless of screw length. Long bicortical screws demonstrate a slight advantage over short monocortical screws in the tested loading conditions. Identifying the optimal stabilization method for the TLJ area, particularly in cases with significant osteoligamentous damage, necessitates a comprehensive analysis of the most common mechanical loading patterns of the spine to minimize surgical risks and the likelihood of fixation failure in both the short and long term.

None.

None.

The authors declare that there are no conflicts of interest.

1. Hallberg I, Bachrach-Lindström M, Hammerby S, et al. Health-related quality of life after vertebral or hip fracture: a seven-year follow-up study. BMC Musculoskelet Disord. 2009;10:135.
2. Oner C, Rajasekaran S, Chapman JR, et al. Spine trauma–what are the current controversies? J Orthop Trauma. 2017;31(Suppl 4):S1–S6.
3. den Ouden LP, Smits AJ, Stadhouder A, et al. Epidemiology of spinal fractures in a level one trauma center in the Netherlands: a 10 years review. Spine (Phila Pa 1976). 2019;44(10):732–739.
4. Saul D, Dresing K. Epidemiology of vertebral fractures in pediatric and adolescent patients. Pediatr Rep. 2018;10(1):7232.
5. Bruno AG, Burkhart K, Allaire B, et al. Spinal loading patterns from biomechanical modeling explain the high incidence of vertebral fractures in the thoracolumbar region. J Bone Miner Res. 2017;32(6):1282–1290.
6. Vialle R, Levassor N, Rillardon L, et al. Radiographic analysis of the sagittal alignment and balance of the spine in asymptomatic subjects. J Bone Joint Surg Am. 2005;87(2):260–267.
7. Vaccaro AR, Oner C, Kepler CK, et al. AOSpine thoracolumbar spine injury classification system: fracture description, neurological status, and key modifiers. Spine (Phila Pa 1976). 2013;38(23):2028–2037.
8. Hoffmann R, Kandziora F, Korge A, et al. Spine trauma treatment: recommendations of the German society for orthopaedics and trauma (DGOU). Global Spine J. 2018;8(2 Suppl):4S.
9. Kepler CK, Vaccaro AR, Schroeder GD, et al. The thoracolumbar AOSpine injury score. Global Spine J. 2016;6(4):329–334.
10. Joaquim AF, Patel AA, Schroeder GD, et al. A simplified treatment algorithm for treating thoracic and lumbar spine trauma. J Spinal Cord Med. 2019;42(4):416–422.
11. Schroeder GD, Kepler CK, Koerner JD, et al. Can a thoracolumbar injury severity score be uniformly applied from T1 to L5 or are modifications necessary? Global Spine J. 2015;5(4):339–345.
12. Chen C-S, Chen W-J, Cheng C-K, et al. Failure analysis of broken pedicle screws on spinal instrumentation. Med Eng Phys. 2005;27(6):487–496.
13. Mohi Eldin MM, Ali AM. Lumbar transpedicular implant failure: a clinical and surgical challenge and its radiological assessment. Asian Spine J. 2014;8(3):281–297.
14. Nekhlopochyn OS, Cheshuk YV, Vorodi MV, et al. Biomechanical state of the operated thoracolumbar junction in lateroflexion. Terra Orthopaedica. 2022(2(113)):58–67.
15. Nekhlopochyn OS, Verbov VV, Cheshuk IV, et al. The biomechanical state of the thoracolumbar junction with various options of transpedicular fixation under flexion load. Ukrainian Neurosurg J. 2023;29(2):49–56.
16. Nekhlopochyn OS, Verbov VV, Karpinsky MY, et al. Biomechanical evaluation of the pedicle screw insertion depth and role of cross-link in thoracolumbar junction fracture surgery: a finite element study under compressive loads. Ukrainian Neurosurg J. 2021;27(3):25–32.
17. Alimohammadi E, Bagheri SR, Joseph B, et al. Analysis of factors associated with the failure of treatment in thoracolumbar burst fractures treated with short-segment posterior spinal fixation. J Orthop Surg Res. 2023;18(1):690.
18. Polgar K, Viceconti M, O'Connor JJ. A comparison between automatically generated linear and parabolic tetrahedra when used to mesh a human femur. Proc Inst Mech Eng H. 2001;215(1):85–94.
19. Liebschner MA, Kopperdahl DL, Rosenberg WS, et al. Finite element modeling of the human thoracolumbar spine. Spine (Phila Pa 1976). 2003;28(6):559–565.
20. Ayturk UM, Puttlitz CM. Parametric convergence sensitivity and validation of a finite element model of the human lumbar spine. Comput Methods Biomech Biomed Engin. 2011;14(8):695–705.
21. Boccaccio A, Pappalettere C. Mechanobiology of fracture healing: basic principles and applications in orthodontics and orthopaedics. In: Klika V, editor. Theoretical Biomechanics. Croatia: InTech. 2011:21–48.
22. Cowin SC. Bone mechanics handbook. 2nd ed. Boca Raton: CRC Press; 2001.
23. Niinomi M. Mechanical biocompatibilities of titanium alloys for biomedical applications. J Mech Behav Biomed Mater. 2008;1(1):30–42.
24. Rao SS. The finite element method in engineering: Elsevier Science; 2005.
25. Kurowski PM. Engineering analysis with COSMOSWorks 2007: SDC Publications; 2007.
26. Ren EH, Deng YJ, Xie QQ, et al. [Anterior versus posterior decompression for the treatment of thoracolumbar fractures with spinal cord injury:a Meta-analysis]. Zhongguo Gu Shang. 2019;32(3):269–277.
27. Zhu Q, Shi F, Cai W, et al. Comparison of anterior versus posterior approach in the treatment of thoracolumbar fractures: a systematic review. Int Surg. 2015;100(6):1124–1133.
28. Nekhlopochyn OS, Verbov VV, Cheshuk IV, et al. Surgical management of traumatic irreducible spondyloptosis of thoracolumbar junction. Ukrainian Neurosurg J. 2021;27(2):56–64.
29. Burkhard MD, Cornaz F, Spirig JM, et al. Posterior spinal instrumentation and decompression with or without cross-link? N Am Spine Soc J. 2021;8:100093.
30. Shibasaki Y, Tsutsui S, Yamamoto E, et al. A bicortical pedicle screw in the caudad trajectory is the best option for the fixation of an osteoporotic vertebra: An in-vitro experimental study using synthetic lumbar osteoporotic bone models. Clin Biomech (Bristol, Avon). 2020;72:150–154.
31. Xu C, Hou Q, Chu Y, et al. How to improve the safety of bicortical pedicle screw insertion in the thoracolumbar vertebrae: analysis base on three-dimensional CT reconstruction of patients in the prone position. BMC Musculoskelet Disord. 2020;21(1):444.
32. Hoffmeister BK, Smith SR, Handley SM, et al. Anisotropy of Young's modulus of human tibial cortical bone. Med Biol Eng Comput. 2000;38(3):333–338.
33. O'Mahony AM, Williams JL, Spencer P. Anisotropic elasticity of cortical and cancellous bone in the posterior mandible increases peri-implant stress and strain under oblique loading. Clin Oral Implants Res. 2001;12(6):648–657.
34. Abdel-Wahab AA, Alam K, Silberschmidt VV. Analysis of anisotropic viscoelastoplastic properties of cortical bone tissues. J Mech Behav Biomed Mater. 2011;4(5):807–820.
35. Lee CK, Kim YE, Lee CS, et al. Impact response of the intervertebral disc in a finite-element model. Spine (Phila Pa 1976). 2000;25(19):2431–2439.
36. Denozière G, Ku DN. Biomechanical comparison between fusion of two vertebrae and implantation of an artificial intervertebral disc. J Biomech. 2006;39(4):766–775.
37. Wirtz DC, Schiffers N, Pandorf T, et al. Critical evaluation of known bone material properties to realize anisotropic FE-simulation of the proximal femur. J Biomech. 2000;33(10):1325–1330.
38. Krone R, Schuster P. An investigation on the importance of material anisotropy in finite-element modeling of the human femur. SAE International; 2006.
39. Kazembakhshi S, Luo Y. Constructing anisotropic finite element model of bone from computed tomography (CT). Biomed Mater Eng. 2014;24(6):2619–2626.