We begin with Atmosphere Einstein Brownian motions toward Knudsen Gas Boltzmann Kinetic formulism of the fluctuation-dissipation theory and applied the formulism to space travelers reentry vehicles. Early experimental results are estimated on the worst situation upper bound when a reentry vehicle is frictionally passing through a dense atmosphere. In reality, the vehicle has spent more time in a dilute atmosphere space. Accordingly, the fluctuation and dissipation theorem, derived from the Boltzmann kinetic equation, predicted a much less friction heat than the final reentry stage.

We wish to estimate for Astronauts returning to the Earth with limited payload heat shields. In other words, we wonder whether the reentry vehicles bottom with an already 4-meter thick heat insulation layers can sustain the increasing burning off by frictional heating under different returning speed. The heat shield’s about 13-foot-diameter composite structure — located at the bottom, blunt end of the Dragon capsule — is detachable and interchangeable between the reusable spacecraft in SpaceX’s Dragon fleet (e.g. Dragon 1, flew 23 cargo missions to the Int’l Space Station (ISS) between 2010 and 2020 before being retired. SpaceX's CEO, Elon Musk, named the spacecraft after the 1963 song "Puff, the Magic Dragon" by Peter, Paul and Mary. For example, 63 foot tall Falcon-9, used $62 Millions per launch).

Figure 1 Dragon capsule — is detachable and interchangeable between the reusable spacecraft in SpaceX’s Dragon fleet. During a reentry, thermal protection system materials perform in temperature ranges from minus 250 F in the cold soak of space to entry temperatures that reach nearly 3,000 ^oF. Because the thermal protection system is installed on the outside of orbiter skin (used carbon-carbon material that won’t oxidize the outer surface is coated with silicon carbide designed by Rockwell Inc. and, Tom Stoebe of Wash U.), it established the aerodynamics function over the vehicle in addition to acting as the heat shield. The re-entry corridor is a narrow region in space that a re-entering vehicle must fly through. If the vehicle strays above the corridor, it may skip out.

If it stays below the corridor, it may burn up. $F_{drag}=\frac{1}{2}\rho V^2{C}_D A$ , in terms of air density $\rho$  velocity $V$ , drag coefficient $C_D.$  high Mach number collision cylinder with negligible sound speed $v_o;$ $\left(V+v_o\right)\cdot A\cong V\cdot A$ . e.g. H. Julian Allen NASA, Ames Research Center Moffett Field.¹

The shortfall, if any, is that¹ it costs $10,000 to put a pound of payload (over 50 thousand pounds per Spaceship/Satellite in Lower Earth Orbit (LEO) Space Station.² For safety reason we cannot reduce the payload without enough safe -margin for the detachable and interchangeable between the reusable spacecraft.

In this paper, we wish to provide a kinetic estimation with a safe margin from the statistical mechanics viewpoint to take into account the material thermal accommodation coefficient $0<\gamma <1$  changes and the atmosphere molecular distribution function varies $f\left(\overrightarrow{x},\overrightarrow{v},t\right).$  from an extreme rarefied Knudsen gas at an infinite mean free path (mfp) all the way to the hydrodynamics continuum limit. The medium may be expressed in terms of a variable mean free path (mfp) parameter relative to size of the vehicle from infinite to zero. The challenges are two folds.¹ The mean free path (mfp) will change from the dilute collision-less Knudsen gas level at the infinity mfp, all the way to continuum hydrodynamic continuum level. Moreover,² the boundary condition is a variable in terms of Maxwell thermal accommodation coefficient: $0<\gamma <1$ , e.g. of which $(1- \gamma )$ will be specula reflection changing only the normal direction of velocity, the rest $\gamma$  component will be absorbed into the thick insulation wall and reaching the thermal equilibrium with the wall at the variable temperature $T_w\left(t\right)$  and diffusively re-emitted in Maxwell velocity equilibrium

$y=x_o+v_o(t-t_{mfp})+x^2; t>t_{mfp}$

Figure 2 The Smoke comes off in linear free flight until multiple collisions with air molecules to reach parabolic curvature.

$\frac{m}{2} \langle u^2\rangle =\frac{1}{2}{k}_B{T}_w\left(t\right); u_{rms}= \sqrt{\raisebox{1ex}{$k_B{T}_w\left(t\right)$}\!\left/ \!\raisebox{-1ex}{$m$}\right.};$  

$t_{mfp}\cong x_{mfp}/u_{rms}$  

The flower pollens motions are named after the botanist Robert Brown, who first described the phenomenon about two hundred years ago in 1827, in his doctoral thesis, under the supervision of Henri Poincare. Then, in 1905, Albert Einstein published a paper, explained as convincing evidence that atoms and molecules exist in water medium and was further verified experimentally by Jean Perrin in 1908, who was awarded the Nobel Prize in Physics in 1926 "for his work on the discontinuous structure of matter. We will review a probabilistic model of Albert Einstein and Marian Smoluchowski in the statistical mechanics, which converge (in hydrodynamic limit) to Brownian motion. In this way, Einstein was able to determine furthermore the size of atoms, and how many atoms there are in a mole, accordance to Avogadro's law, which is 22.4 liters at standard temperature and pressure with Avogadro number, $6.02\times {10}^{23}$ . The first part of Einstein's theory in 1926 consists in the formulation of a diffusion equation for Brownian particles, in which the diffusion coefficient $D_o$  is related to the mean squared displacement of a Brownian particle, while the second part consists in relating the diffusion coefficient to measurable physical quantities such as friction, absolute temperature $T$ . Since the re-entry vehicle final landing will be mostly likely in Oceans, we shall begin with Albert Einstein the Fluctuation and Dissipation theorem in liquid phase.

The diffusion equation has been derived by Adolf Fick in 1855.from the continuity equation, which states that a change in density is. $\frac{\partial \rho \left(t\overrightarrow{,x}\right)}{\partial t}$ ; $\overrightarrow{J}\equiv -D_o \overrightarrow{\nabla } \rho \left(t.\overrightarrow{x}\right); \frac{\partial \rho \left(t\overrightarrow{,x}\right)}{\partial t}=D_o \overrightarrow{\nabla }\cdot \overrightarrow{\nabla }\rho \left(t\overrightarrow{,x}\right)$ due to inflow and outflow of material where the vector flux of the diffusing material $\overrightarrow{J}$ and the diffusion constant $D_o$  is the proportionality.

Theorem 1: Kinetic derivation of diffusion equation

Given kinetic distribution function $f\left(\overrightarrow{x},\overrightarrow{v},t\right)$ of space-velocity & time, we average away the velocity to derive the spatial density function $\rho \left(\overrightarrow{x},t\right)$

$\rho \left(\overrightarrow{x},t\right)\equiv <f\left(t,\overrightarrow{x},\overrightarrow{v}\right){>}_{\overrightarrow{V}}$ , which will satisfy a diffusion equation $\frac{\partial \rho }{\partial t}=D_o{\overrightarrow{\nabla }}^2\text{ρ };$

In 1855, physiologist Adolf Fick first reported flux $\overrightarrow{j}$ is the diffusion flux, of which the dimension is the amount of substance per unit area per unit time. $\overrightarrow{j}$ measures the amount of substance that will flow through a unit area during a unit time interval. D is the diffusion coefficient or diffusivity. Its dimension is area per unit time.

$\overrightarrow{j}=-D\overrightarrow{\nabla \text{ρ}}; \frac{\partial \rho }{\partial t}+\overrightarrow{\nabla }\cdot \overrightarrow{j}=0; \frac{\partial \rho }{\partial t}=D{\overrightarrow{\nabla }}^2\text{ρ }$  

Kinetic theory would begin that a regional time changes equals to its spatial change. The temporal density function $\rho \left(\overrightarrow{x},t\right)$ change in finite time $\tau$ must equal to its spatial changes:

Proof:

$\rho \left(\overrightarrow{x},t\right)+\frac{\partial \rho }{\partial t}){{\displaystyle \int }}^{\text{}}\phi \left(\overrightarrow{\Delta }\right)d\overrightarrow{\Delta }= \frac{\partial \rho }{\partial \overrightarrow{x}}{{\displaystyle \int }}^{\text{}}\phi \left(\overrightarrow{\Delta }\right)\overrightarrow{\Delta } d\overrightarrow{\Delta }+\frac{1}{2}\frac{\partial }{\partial \overrightarrow{x}}\cdot \frac{\partial \rho }{\partial \overrightarrow{x}} \left({{\displaystyle \int }}^{\text{}}\phi \left(\overrightarrow{\Delta }\right)\left|\overrightarrow{\Delta }\cdot \overrightarrow{\Delta } \right|d\overrightarrow{\Delta }\right);$  $\frac{\partial \rho }{\partial t}=D_o{\overrightarrow{\nabla }}^2\text{ρ}$

where diffusion constant $D_o\equiv \frac{1}{2}\langle {\left|\overrightarrow{\Delta }\right|}^2\rangle$ with jump $\overrightarrow{\Delta }$ probability density ${{\displaystyle \int }}^{\text{}}\phi \left(\overrightarrow{\Delta }\right)d\overrightarrow{\Delta }=1.$

Theorem 2: Solving the diffusion equation $\frac{\partial \rho }{\partial t}=D_o{\overrightarrow{\nabla }}^2\text{ρ }$

Assuming the reentry space craft $A\left(\overrightarrow{x},t=0\right)$ in the vast space may be represented by Dirac delta generalized function $\delta \left(\overrightarrow{x}\right)$ If $A\left(\overrightarrow{x},t=0\right)=\delta \left(\overrightarrow{x}\right), then a_{\overrightarrow{k}}\left(0\right)=1$  in terms of its Fourier transforms. We will adopt Fourier transform to replace the Laplacian operator ${\overrightarrow{\nabla }}^2\leftrightarrow {\overrightarrow{k}}^2$  

$A\left(\overrightarrow{x},t\right)\equiv {{\displaystyle \int }}^{\text{}}d\overrightarrow{k}{a}_{\overrightarrow{k}}\left(t\right)e^{i\overrightarrow{k}\overrightarrow{x}} ; a_{\overrightarrow{k}}\left(t\right)\equiv \frac{1}{{(2\pi )}^3}{{\displaystyle \int }}^{\text{}}d\overrightarrow{x}{e}^{-i\overrightarrow{k}\overrightarrow{x}}A\left(\overrightarrow{x},t\right);$  

the diffusion equation is the Fourier space

$\frac{1}{{(2\pi )}^3}{{\displaystyle \int }}^{\text{}}d\overrightarrow{k}{e}^{i\overrightarrow{k\cdot }\overrightarrow{x}}[\frac{d{a}_{\overrightarrow{k}}}{dt}+D_o{k}^2{a}_{\overrightarrow{k}}]=0$

Since the first order time integral gives an exponential function, then $\frac{d{a}_{\overrightarrow{k}}}{dt}+D_o{k}^2{a}_{\overrightarrow{k}}=0$ ; yields the final answer: $a_{\overrightarrow{k}}=$ $a_{\overrightarrow{k}}\left(0\right)\text{exp}\left(-D_o{k}^{2}t\right)$ = $\text{exp}\left(-D_o{k}^{2}t\right)$  in the Fourier space, equivalently in the spatial domain:

$A\left(\overrightarrow{x},t\right)={{\displaystyle \int }}^{\text{}}\frac{d\overrightarrow{k}}{2\pi }\text{exp}\left(i\overrightarrow{k}\overrightarrow{x}\right)\text{exp}\left(-D_o{k}^{2}t\right)$ ; Q.E.D.

Since the rocket thrust must be sufficient to take care the mass weight of rocket, we can avoid involve the computation with mass, geometry, etc. consideration. We will concentrate on the kinetic collision boundary condition. Thus, for geometry simplicity of all kind of reentry vehicles, we develop the molecular fluctuation dissipation theorem, e.g. French Physics Maurice Couette suggested simplified object geometry, i.e. one plate moves with respect to the other plate with gases between two plates. Now we wish to verify the boundary condition based on molecular thermal motion as the origin of the fluctuations. Its local property shall have nothing to do with the geometry object of immersed object and its boundary interaction condition.

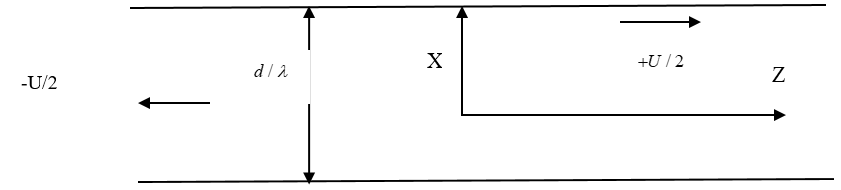
Figure 3 Plane couette flow, $u\equiv U{(\frac{2K_{B}T}{m})}^{\frac{1}{2}}$ ; distance in terms of the mean free path $\lambda ={(n_o \sigma )}^{-1}$  interns of number density $n_o$ , and molecular collision cross section $\sigma$ .

We can prove the fluctuation and dissipation theorem without further ado; A solid body of mass M under Brownian motion is described by Paul Langevin (1832)-Newton force F(t) equation of the acceleration of the velocity $u$ , and friction constant $\beta$  of which the total force $F_T\left(t\right)\equiv \langle F\left(t\right)\rangle +\tilde{F}\left(t\right)$ : we will derive the fluctuation-dissipation theorem from the equal partition law in the isotropic1-D motion:

$M\frac{du}{dt}=-\beta u+\tilde{F}\left(t\right);\langle F\left(t\right)\rangle =-\beta u;\tilde{F}\left(t\right)\equiv F_T\left(t\right)- \langle F\left(t\right)\rangle ;\langle \tilde{F}\left(t\right)\check{F}\left(t^{\prime }\right)\rangle =2D_o\delta \left(t-t"\right)$ ;

$<u\left(t\right){>}^{u_o}=u_o\exp \left(-\frac{\beta }{M}t\right)+W[1-\text{exp}\left(-\frac{\beta }{M}t\right);\lim \text{t}\to \infty ;<u\left(t\right){>}^{u_o}\to W$  

$<(\text{u - W) }\left(u^{\prime }-W\right)>=\langle \left(u-W\right)\rangle \langle \left(u^{\prime }-W\right)\rangle +\frac{D}{\beta M}\text{{}\exp (-\frac{\text{β}}{\text{M}}|t-t^{\prime }|\text{)}-\exp (-\frac{\text{β}}{\text{M}}|t+t^{\prime }|)\};$  

Setting the equal partition law per degree of freedom:

$\underset{t\to \infty }{\text{ lim}}\frac{M}{2}<{(u-W)}^2>=\frac{D_o}{2\beta }=\frac{1}{2}{k}_{B}T$ ,

we have derived the fluctuation –dissipation theorem. $D_o=k_{B}T\beta$ ;

$\tilde{F}\left(t\right)\check{F}\left(t^{\prime }\right)>=2k_{B}T\beta \delta \left(t-t"\right);$  

The devil of fluctuation-dissipation truth is in the detail of molecular-boundary collisions and inter-collisions.

1. Fluctuating Kinetic Theory of discrete molecular phase space $f\left(\overrightarrow{x},\overrightarrow{v},t\right)$ formulation augmented the Ludwig Boltzmann Integral-differential equation with fluctuation Fox sources. We shall simplify the collision kernel by L. Bhatnagar, E.P. Gross, M. Krook (BGK) relaxation equation{2} (Am. Math Soc. Providence RI, 1963, Ch. IV), and keep the fluctuation Fox sources $\widetilde{S }\left(t, \overrightarrow{v}\right)$ (The Rockefeller Univ. 1970 Thesis of Ronald Fox)

$\frac{\partial f}{\partial t}+{\overrightarrow{v}}_{\alpha }\frac{\partial f}{\partial x_{\alpha }}={\left(\frac{\partial f}{\partial t}\right)}_{Col.}\cong -\frac{f-f^{\left(o\right)}}{{\theta }_o}+ \widetilde{S }\left(t, \overrightarrow{v}\right);$  

$\widetilde{S }\left(t, \overrightarrow{v}\right)\widetilde{S }\left(t\text{'}, {\overrightarrow{v}}^{\text{'}}\right)>=\delta \left(t-t^{\prime }\right)\delta (\overrightarrow{v}-{\overrightarrow{v}}^{\text{'}}\}$  

Where in the LHS, we have omitted the acceleration force term ${\overrightarrow{a}}_{\alpha }\frac{\partial f}{\partial {\overrightarrow{v}}_{\alpha }}$ while in the RHS we have simplified the Boltzmann collision term with Stoke Ansatz collision kernel by the BGK relaxation decay model:

$f^{\left(o\right)}=n{(\frac{m}{2\pi K_{B }T})}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2 $}\right.}{e}^{-\frac{m}{2K_{B }T}{(v-u)}^2}$  

First of all we must introduce a fluctuation sources at solid boundary condition. Our goal is to demonstrate for an arbitrary Maxwell accommodation coefficient for absorbed and reemitted condition with the probability $0 <\gamma \le 1$  that a Maxwellian distribution by the plate temperature dynamic condition

$f^{\left(o\right)}\left(\pm \frac{\alpha }{2};c\right)=n_o{(\frac{m}{2K_{B}T})}^{\frac{3}{2}}\text{exp}\left[-c_x^2-c_y^2-\left(c_z\pm \frac{U}{2}{)}^2\right]\cong f_{o }\cdot \left[1 \pm c_{z }U\right)+ O\left(U^{2 }\right)\right]$  

Before fluctuation and dynamic case, we first analyze equilibrium case that a stationary flow and the plate at the same temperature and a constant density of gas:

$\frac{\partial h}{\partial \tau }=0; \left(1,h\right)=\left(c^2-\frac{3}{2}, h\right)=0; g\left(x\right)=\frac{2}{U}\left(c_z,h\right); g\left(x\right)=-g\left(-x\right)$  

Linearized BGK equation for Cuette flow becomes

$c_{x }\frac{\partial h}{\partial x}+ h=c_{z }Ug\left(x\right)$  

This must add boundary condition $h^{+}\left(x, c_x\right)$  and $h^{-}\left(x, -c_x\right)$

We can write the Maxwell boundary conditions $at \alpha =\frac{d}{\lambda }$ is the inverse Knudsen number, and $\gamma$ is Maxwell thermal accommodation coefficients.

$h^{+}\left(-\frac{\alpha }{2}, c_x\right)=-\gamma c_z U+\left(1-\gamma \right)h^{-} \left(-\frac{\alpha }{2}, -c_x \right)$

$h^{-}\left(+\frac{\alpha }{2}, -c{\text{'}}_x\right)=+\gamma c_z U+\left(1-\gamma \right)h^{+} \left(+\frac{\alpha }{2}, c_x^{\text{'}} \right)$

Solution of Fluctuation and Dissipation Relationship with BGK Boltzmann integral-differential equation with Fox sources, under an arbitrary Maxwell thermal accommodation $0<\gamma \le 1$ has been first given by Harold Szu’s dissertation in 1971 under Prof. George E. Uhlenbeck at the Rockefeller Univ. (Unpublished), the results can be compared with experiment data done by NASA and SpaceX Shuttle flights.

$f^{\left(o\right)}\left(\pm \frac{\alpha }{2}, c\right)=n_o {(\frac{m}{2K_B T})}^{\frac{3}{2}} \text{exp}[-c_{x }^2-c_y^2-\left(c_{z }\pm \frac{U}{2}{)}^{2 }\right]=f_o\left( 1\pm c_{z}U\right)+O\left(U^2\right)$  

The complete Fluctuation-Dissipation solution can be found in Ph D dissertation of Harold Szu, Rockefeller University, 1971 (unpublished).

Further lab work

We shall estimate the Shuttle payload mass its average heat capacity of soil compared to the common sense, water 4,18 Joules of heat (1 kilocalorie) for the temperature of one kilogram of water to increase 1°C The specific heat of possible shuttle materials are listed in the following table specific heat defined as follows

[https://en.wikipedia.org/wiki/Specific_heat_capacity]

${\mathcal{C}}_o\equiv \frac{\mathcal{C}}{M}=\frac{1}{M }\frac{dQ}{dT}$  

Specific Heat ${\mathcal{C}}_o$  capacity at a const. pressure versus const. volume (${\beta }_T$ isothermal compressibility, $\alpha$ coeff. Of thermal expansion; $ℂ\text{op}-{\text{C}}_{\text{oV}}=\frac{{\text{α}}^2\text{T}}{{\text{ρβ}}_{\text{T}}}$  

Silicon won’t oxidize in the outer surface, as it is coated with silicon carbide designed by about 13-foot-diameter composite structure and 4 meter thick provided a burn-off mass generating the heat thermal energy should be equivalent, its general proof in the Appendix A.

The conclusions and future works are given as follows: Some suggestions are put forward to measure how we can reduce realistically due to the NASA and SpaceX used the worst situation at the hydrodynamic continuum limit to estimate the $F_{drag}=\frac{1}{2}\rho V^2{C}_D A$ and used about $62 Millions per launch to the LEO Space Station. It seems to be overestimated the need of heat insulation material from the original 13-foot-diameter composite structure to 30% reduction as follows: $4x30\text{\%}=\text{1}\text{.2}$  meter thick. Such a dilute gas kinetic theory reduction can be justified to the reduction of burn-off Silicon Carbide. Thus we compute to be: $4-1.2=2.8$  meter thick Silicon Carbide. Then, the estimated reduction of cost is about $62Mx30%=18.6M, consequently, 62-18.6=43.4M per lunch. We conclude that NASA and SpaceX shall go back to the drawing board to redesign the heat insulator at the Dragon feet.

None.

None.

The author declares no conflicts of interest.

1. THE AERODYNAMIC HEATING OF ATMOSPHERE ENTRY VEHICLES - A REVIEW By H. Julian Allen NASA, Ames Research Center Moffett Field, California Paper for Symposium on Fundamental Phenomena in Hypersonic Flow, Cornell Aeronautical Laboratory, Buffalo, New York. June 25-26, 1964.
2. A study detailing the habitability of a nearby exo-planet appears to have caught the attention of SpaceX CEO Elon Musk, who has wished to transform humanity into a mult-planetary species with plans to colonise Mars within the next few decades. (Credit: Anthony Cuthbertson, Yahoo News Tue, June 13, 2023)
3. Bhatnagar PL, Gross EP, Krook M. A model for collision processes in gases. Phys Rev. 1954;94 (1954):511. Bhatnagar-Gross-Krook model. Encyclopedia of Mathematics.
4. The Boltzmann equation, Gyu Eun Lee, https://www.math.ucla.edu/~gyueun.lee/writing/gso_boltzmann.pdf.
5. Harold Hwaling Szu. The dissertation. The Rockefeller Univ. 1971:1–100.

Appendix A the Mass Energy Equivalence Relationship of Albert Einstein

Einstein's mass-energy equivalence becomes important in Space travel, because the payload mass is equivalent to the energy consumption. Conversely, the heat energy consumption is equivalent to the mass energy usage.

$F=\frac{d\left(mv\right)}{dt}=m\frac{dv}{dt}+v\frac{dm}{dt}$   

$\Delta E=\underset{0vacuum}{\overset{f}{{\displaystyle \int }}}F\cdot ds=\underset{0 }{\overset{f}{{\displaystyle \int }}}\left(m\frac{dv}{dt}+v\frac{dm}{dt}\right) \cdot ds=\underset{0 }{\overset{f}{{\displaystyle \int }}}mv\cdot dv+\underset{0}{\overset{f}{{\displaystyle \int }}}v\frac{dm}{dt} \cdot ds=\frac{1}{2}\underset{0 }{\overset{f}{{\displaystyle \int }}}md\left(v^2\right)+\underset{0}{\overset{f}{{\displaystyle \int }}}{v}^{2}dm$  

Lorentz transform

$m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$   $v^2=c^2\left(1-\frac{m_o^2}{m^2}\right)$   $\frac{d\left(v^2\right)}{dm}=\frac{2m_{o }^2{C}^2}{m^3}$

$\Delta E=\frac{1}{2}\underset{0 }{\overset{f}{{\displaystyle \int }}}md\left(v^2\right)+\underset{0}{\overset{f}{{\displaystyle \int }}}{v}^{2}dm=\underset{0}{\overset{f}{{\displaystyle \int }}}m\frac{m_{o }^2{C}^2}{m^3}dm+\underset{0}{\overset{f}{{\displaystyle \int }}}{c}^2\left(1-\frac{m_o^2}{m^2}\right)\text{dm}=\underset{0}{\overset{\text{f}}{{\displaystyle \int }}}{c}^2\text{dm}$  

$\because \Delta E=C^2\Delta m$ ; $\therefore E=m{C}^2$  Q.E.D.

Verification of Lorentz transform in terms of slow speed limit as follows:

$E=\frac{m_{0 }{C}^2}{\sqrt{1-\frac{v^2}{c^2}}}\cong m_{0 }{C}^2\left\{1+\frac{1}{2}\frac{v^2}{c^2}+\frac{3}{8}\frac{v^4}{c^4}+\dots \right\}=m_{0 }{C}^2+\frac{1}{2}{m}_{0 }{v}^2+\frac{3}{8}{m}_{0 }\frac{v^4}{c^2}$

where the first term is zero velocity mass energy equivalence, and the second term is Newtonian kinetic energy, etc.

Appendix B Fluctuation-Dissipation Theory Estimated by BGK collision kernel.

There is more scientific eluciation in the 1971 Harold Szu PhD thesis of 100 pages (cf. Reference 5). For example, besides the bulk entropy source fluctuation that Ronny Fox derived and discussed in his 1970 Rockefeller Univ. PhD thesis, there are the boundary wall fluctuations that Harold Szu derived and discussed in  a dilute atmosphere medium where Fox"s molecular collisions become rare, but the Szu's boundary fluctuations due to dilute molecular collision become important, and thus the Couette plate were chosen to demonstrate the boundary effect in a dilute gas case. 

$\frac{\partial f}{\partial t}+{\overrightarrow{v}}_{\alpha }\frac{\partial f}{\partial x_{\alpha }}={\left(\frac{\partial f}{\partial t}\right)}_{Col.}\cong -\frac{f-f^{\left(o\right)}}{{\theta }_o}+ \widetilde{S }\left(t, \overrightarrow{v}\right);$  

$\widetilde{S }\left(t, \overrightarrow{v}\right)\widetilde{S }\left(t\text{'}, {\overrightarrow{v}}^{\text{'}}\right)>=\delta \left(t-t^{\prime }\right)$  

For the plane Couette flow, the stochastic BGK equations can be simplified to:

$\frac{\partial h}{\partial \tau }+c_x\frac{\partial h}{\partial x}=-h+2c_z\left(c_z,h \right)+ \widetilde{B }\left(\overrightarrow{x}, \overrightarrow{c},\tau \right)$ ;  $\langle \tilde{B}\rangle =0$

$<\tilde{B} \left(\overrightarrow{x},\overrightarrow{c},\tau \right) \tilde{B} \left({\overrightarrow{x}}^{\text{'}},{\overrightarrow{c}}^{\text{'}},{\tau }^{\prime }\right) \ge \frac{2}{n_o{\lambda }^{ 3}} [{\pi }^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \text{exp} ( \frac{1}{2}\left( \left|\overrightarrow{c}{|}^2+\right|{\overrightarrow{c}}^{\text{'}}{|}^2 \right)$   $\delta \left(\overrightarrow{c}-\overrightarrow{c}\text{'}\right)-2\overrightarrow{c_z} {\overrightarrow{c_z}}^{\text{'}}]$

$\delta \left(\overrightarrow{x}-\overrightarrow{x^{\prime }}\right)\delta \left(\tau -{\tau }^{\prime }\right)$ ];

Putting $h=\langle h\rangle +\left[h-\langle h\rangle \right]\equiv \langle h\rangle +\tilde{h}$ and assuming $\langle h\rangle$ independent of $\tau$ , one gets back for $\langle h\rangle :$  

$c_x\frac{\partial \langle h\rangle }{\partial x}=-\langle h\rangle +2c_z\left(c_z,\langle h\rangle \right)$ ; while for $\tilde{h}\left(x,\overrightarrow{c},\tau \right)$ , one obtains

$\frac{\partial \tilde{h}}{\partial \tau }+c_x\frac{\partial \tilde{h}}{\partial x}=-\tilde{h}+2c_z\left(c_z,\tilde{h} \right)+ \widetilde{B }$  

Note that

(1) Since the correlation of fluctuation source $\widetilde{B }$  is related to the collision kernel $K\left(\overrightarrow{c},\overrightarrow{c^{\prime }}\right)$ if the intermolecular collision can be neglected in the Knudsen limit, then the effect of $\widetilde{B }$ will disappear.

(2) The drag depends on the accommodation coefficients $\gamma$ , while the Fox bulk fluctuations are independent of $\gamma$ . So that these fluctuations alone, the fluctuation-dissipation theorem cannot follow.

(3) There is a second source of fluctuation, which is due to the wall called wall fluctuations [Harold Szu 1971]. More details computation will not be presented but found in the dissertation The Rockefeller Univ., 1971, pp.1, 100.