To determine if a given water supply is safe, the source needs to be protected and monitored regularly. There are two broad approaches to water quality monitoring for pathogen detection. The first approach is direct detection of the pathogen itself, for example, the protozoan Cryptosporidium parvum. While it will be more accurate and precise if specific disease-causing pathogens are detected directly for the determination of water quality, there are several problems with this approach. First, it would be practically impossible to test for each of the wide variety of pathogens that may be present in polluted water. Second, even though most of these pathogens can now be directly detected, the methods are often difficult, relatively expensive, and time-consuming (WHO, 1996). Instead, water monitoring for microbiological quality is primarily based on a second approach, which is to test for .indicator organisms. For a classification table created by the author of typical indicator organisms) The indicator microorganisms should fulfill the following criteria Stetler.1 The concept which explains the ultimate destination of rainwater is the sea either directly through run off or indirectly be infiltration and subsurface flow. A system of water movement in the atmosphere or rainfall, dews, hailstones or snowfalls over land as run off. Vertical and horizontal movement underground as infiltration or subsurface and continuous movement of all forms of water is the hydrogeology cycle. In the atmosphere, water vapours condense and may give rise to precipitation. However, not all this precipitation will reach the ground surface; some are intercepted by vegetation cover or surface of building and other structures and then evaporate back into the atmosphere. The precipitation that reaches the ground surface may flow in to stream, lake and ocean, where it will either be evaporated or form seepages intruding in to the ground likewise soil moisture and further percolate downward to underline aquifer where it may be held for several years longer. Groundwater in Nigeria is restricted by the fact that more than half of the country is underlain by crystalline basement rock of pre-cambian era. The main rock types in this geological terrain include igneous and metamorphic rock such as migmatites and granite gneisses. Generally in their unaltered form, they are characterized by low porosity and permeability. Porosity in basement rocks is by induction through weathering while secondary permeability induces by tectonic activities which manifest in form of that often act as conduct path facilitating water movement. In other words, aquiferous zones in the basement terrain include fractured/weathered rocks. The yielding capacity of well, drilled within such rock are always very enormous. (Shitta 2007) Groundwater is the main resource of drinking water in many parts of the world. Contamination resulting from industry, urbanization and agriculture poses a threat to the groundwater quality Amadi.2,3 The task of balancing groundwater protection and economic activities is challenging. Therefore, understanding the effects of different water management strategies and the role of climate change is essential for the sustainable use of coastal groundwater resources (Prasad and Narayana, 2004). According to Olobaniyi and Owoyemi (2006), the coastal regions of the world are the most densely populated areas in the world. More than one third of the world’s populations are living within 100 km of the coastline (Hughes, et al., 1998). At the same time, the coastal regions provide about one third of the world’s ecosystem services and natural capital Aris et al.4 Such growth is accompanied by increasing demand for water supply leading to the over-exploitation of the aquifer system and excessive drainage for land reclamation purposes. Contamination of the groundwater by natural means (seawater intrusion) and through anthropogenic means (human activities) cannot be ruled out in the area. The study is aimed at evaluating the quality of groundwater from the coastal plain-sand aquifer in Port-Harcourt area with the view of determining its suitability for domestic, irrigational and industrial purposes. The heavy industrial and human activities in the area lead to the present study. The aquifer system in the area is largely unconfined, highly porous and permeable and the possibility of anthropogenic interference cannot be completely ignored, hence the need for this study. Port-Harcourt, the ‘garden-city and treasure base of the nation’ is situated about 60km from the open sea lies between longitude 6o55’E to 7o10’E of the Greenwich meridian and latitude 4o38’N to 4o54’N of the Equator, covering a total distance of about 804km2 Akpokodje.5 In terms of drainage, the area is situated on the top of Bonny River and is entirely lowland with an average elevation of about 15m above sea level.6 The topography is under the influence of tides which results in flooding especially during rainy season.7
Climatically, the city is situated within the sub-equatorial region with the tropical monsoon climate characterized by high temperatures, low pressure and high relative humidity all the year round. The mean annual temperature, rainfall and relative humidity are 30oC, 2,300mm and 90% respectively (Ashton-Jones, 1998). The soil in the area is mainly silty-clay with interaction of sand and gravel while the vegetation is a combination of mangrove swamp forest and rainforest.8 Port-Harcourt falls within the Niger Delta Basin of Southern Nigeria which is defined geologically by three sub-surface sedimentary facies: Akata, Agbada and Benin formations.9,10 The Benin Formation (Oligocene to Recent) is the aquiferous formation in the study area with an average thickness of about 2100m at the centre of the basin and consists of coarse to medium grained sandstone, gravels and clay with an average thickness of about 2100m at the centre of the basin and consists of coarse to medium grained sandstone, gravels and clay Etu-Efeotor & Akpokodje.11 The Agbada Formation consists of alternating deltaic (fluvial, coastal, fluviomarine) and shale, while Akata Formation is the basal sedimentary unit of the entire Niger Delta, consisting of low density, high pressure shallow marine to deep water shale.12
The Implicit Scheme Numerical Solution
(1)
But
Velocity, v in meter per second (m/s), and porosity [-].
Thus equation (1) becomes:
(2)
Converting the PDE to its algebraic equivalent equation by applying the finite different approximation technique for the implicit scheme, we obtain as follows.
(3)
(4)
(5)
Substituting equation (3) through (5) into (2) gives:
Or
(6)
For cases where the initial and final conditions are given, boundary condition at the first node can be expressed as:
(7a)
Hence, first node equation is expressed as:
(7b)
(8a)
Similarly, the last node boundary condition is:
(8b)
For ; and for the first instance, we obtain as follows:
:
,
(9a)
,
(9b)
,
(9c)
,
(9d)
,
(9e)
,
(9f)
,
(9g)
,
(9h)
(9i)
Arranging equations (6a) through (6i) in vector matrix gives:
Where:
Hence, at any point with time, the general form of the above equation is presented as:
Numerical Method were applied through the developed system to generate the governing equations, derived solution generated the derived model solution, this were simulated to monitor the contaminants at different depth, values of contaminant known as concentration at different depth were generated, this results are within the values of concentration from other experimental values from the same contaminant by other experts, validation of the developed model is a thorough concept for monitoring such microbes in deltaic environment
Results and discussion are presented in tables including graphical representation for Acetobacter stated below. The study has expressed the behaviour of the Arthrobacter migration under the influences of dispersion in phreatic bed; the lithology of the formation has lots of effect on the rate of transport. Base on these factors,
Figure 1 experiences sudden rapid migration between 5 -10m, thus reduce with increase in depth were the lowest concentration were recorded at 30m. While
Figure 2 maintained similar condition, rapid increase were observed between 0-5m thus sudden decrease were experiences to the lowest rates of concentration recorded at 30m,
Figure 3 experiences exponential phase in the system, the deposition of Arthrobacter experiences maximum rate of concentration at 30m.
Figure 4 maintained gradual increase of the contaminant to where the optimum level was observed at 30m. Figure 5 observed similar condition whereby rapid increase was experiences between 0-5m, while fluctuation was observed from 10-30m (
Tables 1-5).

Figure 1 Simulation Values from Arthrobacter Concentration at Different Depth

Figure 2 Simulation Values from Arthrobacter Concentration at Different Depth

Figure 3 Simulation Values from Arthrobacter Concentration at Different Depth

Figure 4 Simulation Values from Arthrobacter Concentration at Different Depth
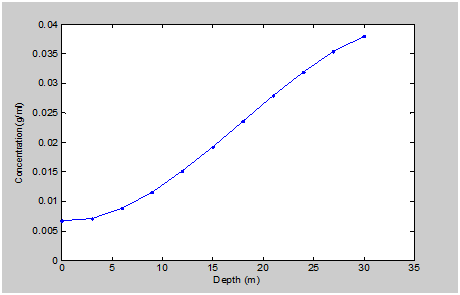
Figure 5 Simulation Values from Arthrobacter Concentration at Different Depth
Depth (m) |
Concentration (g/L) |
0 |
0.653 |
3 |
0.689 |
6 |
0.6526 |
9 |
0.512 |
12 |
0.316 |
15 |
0.125 |
18 |
0.064 |
21 |
0.027 |
24 |
0.008 |
27 |
0.001 |
30 |
0.00025 |
Table 1 Simulation Values from Arthrobacter Concentration at Different Depth
Depth (m) |
Concentration (g/L) |
0 |
0.5543 |
3 |
0.3675 |
6 |
0.2270 |
9 |
0.1263 |
12 |
0.0592 |
15 |
0.0193 |
18 |
0.0036 |
21 |
0.0024 |
24 |
0.0022 |
27 |
0.0015 |
30 |
0.0005 |
Table 2 Simulation Values from Arthrobacter Concentration at Different Depth
Depth (m) |
Concentration (g/L) |
0 |
0.653 |
3 |
0.659563 |
6 |
0.679649 |
9 |
0.714496 |
12 |
0.766303 |
15 |
0.838469 |
18 |
0.935964 |
21 |
1.065902 |
24 |
1.238402 |
27 |
1.467884 |
30 |
1.775038 |
Table 3 Simulation Values from Arthrobacter Concentration at Different Depth
Depth (m) |
Concentration (g/L) |
0 |
0.0956 |
3 |
0.0875 |
6 |
0.0821 |
9 |
0.0794 |
12 |
0.0794 |
15 |
0.0819 |
18 |
0.0869 |
21 |
0.0943 |
24 |
0.1041 |
27 |
0.1163 |
30 |
0.1308 |
Table 4 Simulation Values from Arthrobacter Concentration at Different Depth
Depth (m) |
Concentration (g/L) |
0 |
0.11882 |
3 |
0.1577 |
6 |
0.1691 |
9 |
0.1560 |
12 |
0.1371 |
15 |
0.1074 |
18 |
0.0777 |
21 |
0.0548 |
24 |
0.0457 |
27 |
0.0571 |
30 |
0.0960 |
Table 5Simulation Values from Arthrobacter Concentration at Different Depth
None.


