In this paper, we shall sketch the divide and conquer strategy from LMS error viewpoint on applying world’s largest i-Phone iCloud membership to codec the Digital Cryptographic Currency (DCC) going beyond Bitcoins (BTC) to be a viable alternative with a formidable challenge. In fact, there is plenty benefits to motivate further development. For example, it is possible that there are no third party bank broker fee, no country exchange fee, and no bank robbery. DCC is great for international trade in the Global Economic Investment Environment. DCC is merely some promissory note “I owe you this much and reneging condition is this” in binary bits, which deliberately makes no one else, except relevant trading partners have the private keys can read it.

Keywords: RSA codec, digital crypto currency, pooling I-phones, optical computing

The invention of “BiT Coin (BTC)”, by Satashi Nagamoto circa 2008, remains as a formidable task. There is a plenty of benefits to motivate a further development of BTC without the rare metal material as the token, as the early Digital Crypto Currency (DCC), e.g. (1) Utilized the recently advance in secure codec technology in few more order of magnitude beyond classical hashing and anti-hashing scramble data, in terms of public and private large prime number factorial codec key invented by Rivest, Shamir, Adleman and Cocks (RASC) circa WWII, re-written now for digital Smart Phone or PC that are easy for anyone to do a smart contract in template an essential promissory notes, e.g. “I owe you such under this reneging condition.” The major difference in secured feature is taking the available World Wide Web broadcasting one-way to all memberships in the Cloud. However, only the (1) involved trading partners can read with their private keys, (2) no third party banking or broker fee, (3) no International currency exchange fee, and (4) no one can rob the digital bank, etc. These benefits have been endorsed by Small Business Innovative Research.

DCC, digital cryptographic currency; AI, artificial intelligence; ANN, artificial neural network; MPD, massively parallel and distributed; GPU, graphic processing units; NP, nondeterministic polynomial-time; TSP, travelling salesman problem; MSE, minimum square errors

The National Foundation of Digital Cryptographic Currency plan in a 5 year collaboration effort among the Foundation, the Academia and the Industrial for i-Phone Cloud Pooling computing. The supercomputing power comes from pooling i-Phone’s which it selves are already powerful into a conglomerate of i-phone computing Fan Club. It can solve the Rivest, Shamir, Adleman and Cocks (RASC) cf. Figure 1 security coding-decoding for a very larger prime number factorization. The R/D Computing Tool problems are two folds (i) develop an efficient & real-time divide & conquer of all available i-Phones. We anticipate the international trade bank can do away the third party wasteful exchange rates. Then, the conglomerated i-Phone super-computing might wish even more secure (ii) Utilizing 3-D amplitude and phase interference pattern as the representation of digital bits to solve the same binary RSA, with the help of desk-top miniaturized optical computing similar to Mach-Zehnder fiber optics interference as the representation of a “bit”. This is similar, in vain to National Initiative in Quantum Computing, using both the phase and the amplitude but it is not the same as high temperature superconductor quantum computing in terms of spins angular momentum representation. Artificial Intelligence (AI) based on computational approach using Artificial Neural Network (ANN) have been applied to digital financial data analysis, including helping Stock Markets Investment, airline reservation systems, searching social network relationships, etc. We have early developed Big Data Mining, e.g. finding out Who’s Who behind the international investment used already in World Bank IMC. We have furthermore extended the Page Ranking adopted by Google Search Engine as the asymmetric graph theory that must treat the outgoing relationship as the reputation, while the incoming relationship is the risk. Since DCC needs the public trustworthiness without gold collateral or dollar bills in the National Reserve or anywhere else, we take a massively parallel and distributed (MPD) approach assuming the world largest computer conglomeration namely iPhone with hundred Gigabytes per sec (bps) power each, and a combined power of thousand iPhone members in the cloud, is Terabps much larger than a miniaturized GPU. Furthermore, each iPhone takes Python TensorFlow software in a lossless “divide and conquers” MPD codec for the total conglomeration. In Section 1, we review early BTC which can survive, because there is no obvious challenge against the hashing and inverse hashing codec. This fact is no longer true, because of recent exhaustive search in a fixed finite set hashing and thus threatens the Bitcoin.

Then in Section 2, as alternative to iPhone Cloud and RSAC Codec, we review an alternative Optical Computing in 5 years R/D versus Quantum Computers in 10 years R/D. Despite international investment in quantum computing, distant communication, Google Map pathfinding, and others are not yet ready for quantum computing. We point out our design of multiple stage Mach-Zehnder Interferogram can be effective Optical Computers which will be employed for our DCC based on (i) Representation: 3-D Interference Pattern similar to the Quantum Bit (Qubit), but is not in realization, (ii) Real Time Holography Crystal (e.g. LiNiOB) as the Storage medium, and (iii) Real Time Amplitude Multiplication and phase modulation as the operations.

In Section 3, DCC utilized the computational intractable factorial codec which has the private keys made of RSAC codec when the miniaturized super-computing Graphic Processing Units (GPU) becomes a just a back-plan of a portable PC helping rapid computing.

If we wish to do loss-less divide and conquer strategy in computing, we must know how to take care of the data in chunks such that the total togetherness coherent property is not lost. Also, we wish to warn readerships, the automatic solution to Nondeterministic Polynomial-time (NP) Complete Problems has not been discovered. We can solve these statistically, one at a time, the NP Complete Travelling Salesman Problem (TSP) by using these techniques.

$\text{min}\parallel \stackrel{\rightharpoonup }{{\rm A}}-\stackrel{\rightharpoonup }{{\rm B}}{\parallel }^2=\text{min}\parallel \stackrel{\rightharpoonup }{{\rm A}}-+-\stackrel{\rightharpoonup }{{\rm B}}{\parallel }^2=\text{min}\parallel \stackrel{\rightharpoonup }{{\rm A}}-{\parallel }^2+\text{min}\parallel -\stackrel{\rightharpoonup }{{\rm B}}{\parallel }^2\text{iff }\perp$ (1)

Proof: If $(\stackrel{\rightharpoonup }{{\rm A}}-\overrightarrow{C})\perp (\overrightarrow{C}-\stackrel{\rightharpoonup }{{\rm B}})=0$

Then Eq(1) holds true.

vice versa

Q.E.D.

When solving Traveling Salesman Problem (TSP) for 3 cities, if and only the new node Cityan be found in simpler 1-D boundry search, such that to find the city previously bisected byandcities. Note that there is a trick to add a ghost city C, and then delete the pseudo-triangle made by the ghost city C with the two nearby real Cities in the end. Then, the cost of search for  is linear at the boundary surface of the dimension of N-1. To Read Further: TSP defines a travel salesman visits every M city once and only once. An efficient deterministic solution has not been found. In other words, a statistical solution is not generally transferable to the other search problems, e.g. All TSP, N Queen Problem, Job Shop Problem, etc., We have only solved statistically following Hopfield and Tank by applying the Minimum Square Errors (MSE) cost Function for the ANN Supervised Learning. For example, TSP, Foo and Szu, 1997; Cauchy Machine by Y. Takefuji and H. Szu, Cauchy Machine, Stochastic Search in N dimensions Cauchy statistics by I. Kopriva, H. Szu). Minimum Square Errors (MSE) cost function is statistically supervised learning, Even the general N dimensional vector space of the vector and (e.g. the TSP, N=2, solved stochastically not yet deterministically that otherwise deserves the Turing Prize; for a general TSP the challenge reminds in the NP Complete Grand Schmidt Orthogonal pre-processing of N vectors)

We take the hardware, e.g. recently miniaturized Graphic Processing Units (GPU) to test the Security coding software that is adopted by National Security Agency, known as MIT Patent, RSAC codec before the declassified British Clifford Cocks codec cf. Figure 1 We wish to refer to collectively as the RSAC codec. The characteristics of RSAC remains to be asymmetric keys limited to a large membership group, where their public keys are known to the all memberships, but are different from the key private to each individual members in order to avoid a single point failure. The coding security by the public keys has been already so good that no one except the members who have the public keys can code the message in real time. The decode security is likewise so good that no one except you have the private key, so that no other one else except you can rob your digital bank. Recently, one of the best Stanford PhD thesis has developed a symmetric key to go beyond membership imitation. (Stanford Thesis studied about how to symmetrize the public and private keys of RSA codec.) A shortfall of DCC if any is the psychological trustworthiness. Hollywood style publicity and TED Summit X-series Seminars; Stanford CS Prof. Andrew Ng: Course RA, Inc.; MIT Artificial General Intelligence (AGI) by Prof. Lex Fridman (deep learning, machine learning, You Tube: Stephen Wolfram, Ray Kurzweil), might help promote DCC, but the final acceptance must be earned. lets for the Non-convex Search Engine (NSE) of RSAC large prime number codec as non-solvable Turing Prize NP Complete Problem. We review current state of art technology compared decades ago in hardware and software for financial apps and pointed out the future stable growth direction—digital currency: from ‘BTC’, to ‘digital crypt currency (DCC)’.

Figure 1 MIT Prof. Rivest, Shamir, Adleman and British Prof. Cocks (RASC) (taken from Google Image Search).

We review the monetary system (MS). Ms. Bettina Warburg (Venture Capitalist in Animal) has given a lucid 15 minutes TED Summit in June 2016: “how the blockchain will radically transform the economy;” “The rise of decentralized economy,” (Smart City Expo World Congress, Published on Nov 28, 2017). She began to honor the Nobel Laureate Economics Douglas North who introduced "Institution is to reduce the Uncertainty of Trade,” (rather went back to legacy of Bitcoin inventor(s) by Mr. Satashi Nagamoto circa 2008, and the future decentralized economy is good or bad but inevitable. We can apply powerful PC to simulate the future before we implement the change; DCC to be decentralized, as well as the Internet of Things (IoT) to learn and unlearn.The Venture Capitalist and investment angels must be aware of the concept of DCC before jumping on the BTC Wagon. She went on to describe the story business to business (B2B) protocol infrastructure level, before to B2B of how to reduce the trade uncertainty in three ways in the last decade:

1. Informal---Knife/Weapon,
2. Banking---Checks,
3. Internet/online---Amazon, e-Bay, Alibaba, etc. middleman, that can do away by DCC.

Since DCC is not the money but an equivalence of promised note like bank check records: “I owe you” smart contract resided on all distributed computer nodes, that can do away the third parties of human and government regulation, e.g. banking credit unions, as well as the internationally currency exchange fee.

DCC is decentralized database (DD) “supply chain and middle man,” like checkbook record to all interconnected computers nodes and replicated and distributed throughout the database that no one can change one unless all of them are in their control. It can register the assets and the transactions, with immutable, unforgettable, untamperable, duplicate records. Thus, "BTC technology can reduce the uncertainty." Likewise, the DCC trade has three kinds (Figure 2):

Figure 2 Bits Coins Original Token will be replaced by Digital Crypto Currency without the BC but Promising Notes of equivalent debt in public RSAC codec to be paid back with reneging conditions.

1. Identity: whom we are dealing with profile Identity, user control portable.
2. Asset tracking: transparency on the horizontal supply chain, product evolve vertical chain, all directions are un-trust to one another.
3. Reneging on deal: smart contract cannot release the funds we received as the collateral until completion of the contract (lower uncertainty). In summary: DCC shares the reality, the same databases without trust one another; Mutual distrust among trades can harness the collective uncertainty through DCC technology; rather than slows down the trade. The future remains in the computer science startup company developing the trinity among data, products, and users that generates more labeled data and products, cf. Figure 3 Trade Trinity.

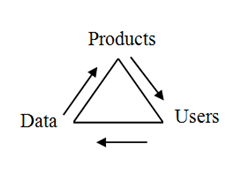
Figure 3 Trade Trinity [Product (Beauty), Truth (Data), Virtue (Users)]: In Business Management the innovation is critical to sustain the business.

Remarks are itemized as follows

MBA defined the innovation to be “finding the gaps and filling in the values.” (Appendix A) Good managers are trained to seek the positive forward loops, by adding the value in manufacturing more data/goods into products, and more users/consumers will purchase the products, and generate more data usage. The more one understands the users, and the products, the business can generate better products. That’s how one can sustain the business in decades. For example, “weight loss” product, user has desire to fulfill. Then, one can put forward advertisement targeted online to the audience and one can earn the commission to do so.

The second aspect is to understand the 2 levels of security “Secret and Top Secret (TS)” that are determined according to National Security Agency (NSA) the significance to national security when it is accidentally breached. In this paper, we took the running time to break the coding, “Secret is a day of supercomputing running time,” “TS is a year supercomputing running time.” These become moving targets and must be revised as computer and software become more powerful. The highest security in business community is the reputation. DCC used the decentralized through Internet that turns out in the “A business is not to earn the money, but the hearts of consumers,” (quote from one the famous Korean soap Operas “Commerce Morality” between China and Korean during Chin Dynasty).

1. Optical Computer is multiple layers of Mach Zender interference by lenslet and beam splitters. One used both the amplitude and the phase of laser light as the natural quantum mechanics representation of Qubits.
2. The real time holography by Lithium Niobate Crystal of 4 wave mixing. This will be the storage Then, 3-D interference patterns are the data representations of Quibit that shall represent that “you owe me such, with the negating condition”.
3. RSAC Codec by Mr. Shor 1994, and Mr. Lov Grover in 2012

The most powerful traditional supercomputer is built by matching hardware with software companies, e.g. Nvidia Inc. and EXXACT. Naval Research Lab has supported John von Neumann to develop 2-D Silicon plan 3^rd Gen Semiconductor computer for easy sharing the ground zero, besides the 1^st Gen Chinese mechanical computer, the 2^nd Gen Semiconductor. The 4^th Gen computer is the Integrated Semiconductor (IC) Blue IBM Computers. The Graphic Processors Units (GPU) has 8 Central Processor Units (CPU) in a rack, and the cube 8x8x8 racks are packed in an air condition room size, which has 4096 CPU’s at the tone of $M. According to the Morse Law, doubling the power in 18 months, the IC chips have been miniaturized from the room size GPU into the Table Top Back-Plan, thus it becomes portable super-PC limited by heat transfer property. The author called the 5^th Gen should be emulating Brain Style 3-D Carbon Computer that has Ten Billion Neurons (each neuron like a CPU) with the help of 100 Billion house cleaning servant non-electrical-conducting Glial cells keeping conducting neurons in layer-by-layer architecture.

1. The Brain Style Computing (BSC) is 3-D Carbon based computing and can compete against 2-D silicon-based computing. Recently, OC employs both the Amplitude and the Phase of laser-like optical wave function. They are different from binary digital electronic computers based on transistors finite state Von Neumann machines. Whereas common digital computing requires that the data be encoded into binary digits (bits), each of which is always in one of two definite states (0 or 1), quantum computation uses quantum bits, which can be in superposition of states.
2. On the other hand, the BSC is developed naturally for the survival Natural Intelligence (NI). BSC Carbon computing enjoys the thermal bath atas part of unwanted signals, where all sensory “power of pairs” eyes, ears, nostrils, tactile, inputs are relaxing toward the equilibrium, in order to extract surviving features: “While disagree, the noise; agree, the signal.” In other words, the noise is just an unwanted signal called the clutters.
3. The third aspect is the Artificial Intelligence (AI) machines to recommend us and make better decisions with informed choices; to users and machines to learn and un-learned that may be based on the same part of brains “Claustrum (Greek: Conductor) Appendix B.
4. The internet of things (IoT) is already here. The emerging smart home is an example of IoT, where the idea is that all the “things” are connected to the internet: refrigerator, TV, thermostat and more. As more and more everyday devices go online, IoT becomes increasingly mainstream and part of daily life. Thanks to a combination of Wi-Fi, data networks and Bluetooth connecting devices (Figure 4).

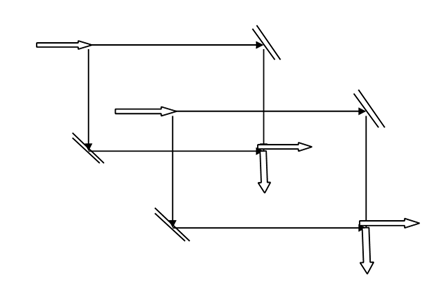
Figure 4 Miniature Optical Computing uses beam splitters laser diodes in a cascade of mirrors of Mach-Zehnder interferometer types.

Verifiable Computation enables a computationally weak client to “outsource” the computation of a function F on various inputs x1,...,xk to one or more workers. Fully homomorphism encryption, we have “Non-Interactive A cryptosystem that supports arbitrary computation on cipher texts is known as fully homomorphic encryption (FHE) and is far more powerful. Such a scheme enables the construction of programs for any desirable functionality, which can be run on encrypted inputs to produce an encryption of the result. Since such a program need never decrypt its inputs, it can be run by an untrusted party without revealing its inputs and internal state. Fully homomorphic cryptosystems have great practical implications in the outsourcing of private computations, for instance, in the context of cloud computing.¹The problem of constructing a fully homomorphic encryption scheme was first proposed in 1978, within a year of the development of RSAC.² For more than 30 years, it was unclear whether a solution existed. During that period, partial results included the Sander-Young-Yung system, which solved the problem for logarithmic depth circuits;³ the Boneh–Goh–Nissim cryptosystem, which supports evaluation of an unlimited number of addition operations but at most one multiplication;⁴ and the Ishai-Paskin cryptosystem, which supports evaluation of polynomial-size branching programs.⁵ Early homomorphism cryptosystems, and Gentry's cryptosystem proposed by Craig Gentry⁶ used the lattice-based cryptography, described the first plausible construction for a fully homomorphic encryption scheme. Gentry's scheme supports both addition and multiplication operations on cipher-texts, from which it is possible to construct circuits for performing arbitrary computation. The construction starts from a somewhat homomorphism encryption scheme, which is limited to evaluating low-degree polynomials over encrypted data. (It is limited because each cipher-text is noisy in some sense, and this noise grows as one adds and multiplies cipher-texts, until ultimately the noise makes the resulting ciphertext indecipherable.) Gentry then shows how to slightly modify this scheme to make it bootstrap-able, i.e., capable of evaluating its own decryption circuit and then at least one more operation. Finally, he shows that any bootstrap-able somewhat homomorphic encryption scheme can be converted into a fully homomorphic encryption through a recursive self-embedding. For Gentry's "noisy" scheme, the bootstrapping procedure effectively "refreshes" the cipher-text by applying to it the decryption procedure homomorphically, thereby obtaining a new cipher-text that encrypts the same value as before but has lower noise. By "refreshing" the cipher-text periodically whenever the noise grows too large, it is possible to compute arbitrary number of additions and multiplications without increasing the noise too much. Gentry based the security of his scheme on the assumed hardness of two problems: certain worst-case problems over ideal lattices, and the sparse (or low-weight) subset sum problem. Gentry's PhD thesis provides additional details. Regarding performance, cipher-texts in Gentry's scheme remain compact insofar as their lengths do not depend at all on the complexity of the function that is evaluated over the encrypted data, but the scheme is impractical, and its cipher-text size and computation time increase sharply as one increases the security level. Several optimizations and refinements were proposed by Damien Stehle and Ron Steinfeld, Nigel Smart and Frederick Vercauteren, and Craig Gentry and Shai Halevi, the latter obtaining the first working implementation of Gentry's fully homomorphic encryption.

The prime numbers must be kept secret. Anyone can use the public key to encrypt a message, but with currently published methods, and if the public key is large enough, only someone with knowledge of the prime numbers can decode the message feasibly. In such a cryptosystem, the encryption key is public and it is different from the decryption key which is kept secret (private). In RSAC, this asymmetry is based on the practical difficulty of the factorization of the product of two large prime numbers, the "factoring problem", based on the multiplier  of two prime numbers: .

Then the public keys $\left(n,e\right)$ ; and private keys$\left(n,\text{ d}\right)$

$Letp=2,q=3;thenpq=n=6$ (2)

The encryption prime number $e=3$ is chosen by satisfying greatest common divisor (gcd)

$\left(e,\left(p-1\right)\left(q-1\right)\right)=gcd\left(3,1*2\right)=1$ (3)

Let the message  be the alphabetic order of English letter. Then the constraint with 0 ≤ m < n. We can only code very simple language: Bob is shy and wishes to send to Alice “I L” for “I Love”, namely Bob follow Caesar cipher converting the English letters into their numerical equivalents (alphabet order-1). Since “3” for “C” of “Come” [&”5” for “E” of “Equal”, “7” for “G” of “Go”], then

$m=\left(5-1\right)=4.$ (4)

The RSAC algorithm involves four steps: key generation, key distribution, encryption and decryption. A basic principle behind RSAC is the observation that it is practical to find three very large positive integers e, d and n such that with modular exponentiation  for all (A familiar use of modular arithmetic is in the 12-hour clock, in which the day is divided into two 6-hour periods)

${(m^e)}^d=mmod\left(n\right)$ (5)

${(4^3)}^d={(4^3)}^2={56}^2=3136=?4mod\left(6\right)=64-4=60=\left(6x10\right)$

And that even knowing  and  or even  it can be extremely difficult to find =

In addition, for some operations it is convenient that the order of the two exponentiations can be changed and that this relation also implies:

${(m^d)}^e=mmod\left(n\right)$ (6)

RSAC involves a public key and a private key Eq (7). The public key can be known by everyone, and it is used for encrypting messages. The intention is that messages encrypted with the public key can only be decrypted in a reasonable amount of time by using the private key. The public key is represented by the integers (int.)  and ; and, the private key, by the int. (although is also used during the decryption process.

$Publickey=int.\left(n,e\right)$ ;$Privatekey=int.\left(n,d\right);forall$ int. message m (with 0 ≤ m < n) (7)

Thus, it might be considered a part of the private key, too.represents the message that was previously prepared with a certain technique explained below.

The public key can be known by everyone, and it is used for encrypting messages. The intention is that messages encrypted with the public key can only be decrypted in a reasonable amount of time by using the private key. The public key is represented by the integersandand, the private key, by the integer(although n is also used during the decryption process. Thus, it might be considered a part of the private key, too). m represents the message (previously prepared with a certain technique explained below). Adi Shamir makes 15 predictions (Appendix C) where Block Chain might survive Bitcoin legacy: "Financial Cryptography: Past, Present, and Future" at Financial Cryptography 2016.

RSAC Encryption using Alphabetic order known as Caesar cipher

We select 2 small primes, p=3 & q=5 (normally supercomputer uses 200 decimals primes which needs the probabilistic prime determination methods) so that n=3·5=15, and with encoding key e=7, $n=\left(3-1\right)\left(5-1\right)=8$

$gcd\left(e,\left(p-1\right)\left(q-1\right)\right)=gcd\left(7,2\text{*}4\right)=1$

Encryption public key $\left(e,n\right)=\left(7,8\right)$ ; private key $\left(d,n\right)=($

(gcd = greatest common divisor)

Let’s take the hypothetical Bob (B) to Alice (A) message M= “STOP,”

First, we'll convert the letters S is #19-1=18; T is #20-1=19; O is #15-1=14; P is #16-1=15.

Into their numerical equivalents (position in the alphabet-1) and then group those numbers into blocks of 4.

M=1819 1415 = ST OP

We encrypt each block using the mapping:

C = M13 mod 2537

Computations using modular multiplication show that

181913 mod 2537=2081, and 141513 mod 2537=2182.

The encrypted message is thus

M’=2081 2182.

RSAC Decryption key d

The plaintext message can be quickly recovered when the decryption key, d

an inverse of  modulo $\left(p-1\right)\left(q-1\right)$ is known.

(Such an inverse exists since $gcd\left(e,\left(p-1\right)\left(q-1\right)\right)=1)$ .

Using the simple cipher above we receive the message 0981 0461, let’s go about decrypting it.$n = 43 · 59 and e \left(exponent\right) = 13$ ,

we can work out that

$d = 937$ is an inverse of $13 modulo 42 · 58 = 2436$ .

We therefore useas our decryption exponent, therefore.

$P = C937 mod 2537$

Using fast modular exponentiation (an algorithm) we compute

$0981937 mod 2537, = 0704$ and $0461937 mod 2537 = 1115$ .

Quick translation reveals that this message N’ from Alice to Bob:$N=HELP$ .

In 2010, Marten van Dijk, Craig Gentry, Shai Halevi and Vinod Vaikuntanathan presented a second fully homomorphism encryption scheme, which uses many of the tools of Gentry's construction, but which does not require ideal lattices. Instead, they show that the somewhat homomorphism component of Gentry's ideal lattice-based scheme can be replaced with a very simple somewhat homomorphism scheme that uses integers. The scheme is therefore conceptually simpler than Gentry's ideal lattice scheme, but has similar properties with regards to homomorphism operations and efficiency. The somewhat homomorphism component in the work of van Dijk et al. is similar to an encryption scheme proposed by Levieil and Naccache in 2008, and also to one that was proposed by Bram Cohen in 1998. Cohen's method is not even additively homomorphism, however. The Levieil–Naccache scheme supports only additions, but it can be modified to also support a small number of multiplications. Many refinements and optimizations of the scheme of van Dijk et al. were proposed in a sequence of works by Jean-Sébastien Coron, Tancrède Lepoint, Avradip Mandal, David Naccache, and Mehdi Tibouchi. Some of these works included also implementations of the resulting schemes.

The 2nd generation of homomorphism cryptosystems

Several new techniques that were developed starting in 2011-2012 by Zvika Brakerski, Craig Gentry, Vinod Vaikuntanathan, and others, led to the development of much more efficient somewhat and fully homomorphic cryptosystems. These include: The Brakerski-Gentry-Vaikuntanathan cryptosystem (BGV), building on techniques of Brakerski-Vaikuntanathan. Brakerski's scale-invariant cryptosystem. The NTRU-based cryptosystem due to Lopez-Alt, Tromer, and Vaikuntanathan (LTV). The Gentry-Sahai-Waters cryptosystem (GSW). The security of most of these schemes is based on the hardness of the Learning with errors problem, except for the LTV scheme whose security is based on a variant of the NTRU computational problem. The distinguishing characteristic of these cryptosystems is that they all feature much slower growth of the noise during the homomorphism computations. Additional optimizations by Craig Gentry, Shai Halevi, and Nigel Smart resulted in cryptosystems with nearly optimal asymptotic complexity. These optimizations build on the Smart-Vercauteren techniques that enable packing of many plaintext values in a single cipher-text and operating on all these plaintext values in a SIMD fashion. Many of the advances in these second-generation cryptosystems were also ported to the cryptosystem over the integers.

Zvika Brakerski and Vinod Vaikuntanathan observed that for certain types of circuits, the GSW cryptosystem features an even slower growth rate of noise, and hence better efficiency and stronger security.[30] Jacob Alperin-Sheriff and Chris Peikert then described a very efficient bootstrapping technique that uses exactly this type of circuits[31] This type of circuits, however, seems incompatible with the ciphertext-packing techniques, and hence the Gentry-Halevi-Smart optimizations cannot be applied here. All the second-generation cryptosystems still follow the basic blueprint of Gentry's original construction, namely they first construct a somewhat-homomorphic cryptosystem that handles noisy cipher-texts, and then convert it to a fully homomorphic cryptosystem using bootstrapping. The first reported implementation of fully homomorphism encryption is the Gentry-Halevi implementation mentioned above of Gentry's original cryptosystem, they reported timing of about 30 minutes per basic bit operation. The second-generation schemes made this implementation obsolete, however. Many implementations of second-generation somewhat-homomorphism cryptosystems were reported in the literature. An early implementation (from 2012 due to Gentry, Halevi, and Smart (GHS) of a variant of the BGV cryptosystem) was reported of a complex circuit (implementing the encryption procedure of the AES cipher) in 36hours. Using the packed-cipher-text techniques, that implementation could evaluate the same circuit on 54 different inputs in the same 36hours, yielding amortized time of roughly 40minutes per input. This AES-encryption circuit was adopted as a benchmark in several follow-up works, gradually bringing the evaluation time down to about fourhours and the per-input amortized time to just over 7seconds. Three implementations of second-generation homomorphism cryptosystems are available in open source libraries:

The HElib library due to Shai Halevi and Victor Shoup that implements the BGV cryptosystem with the GHS optimizations, the FHEW library [35] due to Leo Ducas and Daniele Micciancio that implements a combination of Regev's LWE cryptosystem with the bootstrapping techniques of Alperin-Sheriff and Peikert, and the TFHE library due to Ilaria Chillotti, Nicolas Gama, Mariya Georgieva and Malika Izabachene that proposes a faster variant over the Torus with an intuitive API to evaluate boolean circuits. All these libraries implement fully homomorphism encryption including bootstrapping. HElib reports time of 5–10minutes for bootstrapping a packed cipher-text with about 1000 plaintext values, FHEW reports time of around 1/2second for bootstrapping a non-packed ciphertext encrypting a single bit, and TFHE reports time of 13milliseconds for evaluating any bootstrapped binary gate on non-packed cipher-texts encrypting a single bit. In late 2014, a re-implementation of homomorphism evaluation of the AES-encryption circuit using HElib, reported evaluation time of just over four minutes on 120 inputs, bringing the amortized per-input time to about 2 seconds (Figure 5).

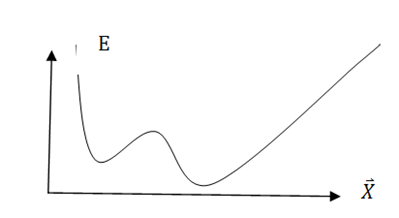
Figure 5 Causality: local minimum and initial condition, Nonconvex Energy Landscape, the horizontal vector abscissas could be the input sensor vectors. Applying Fast Cauchy cooling simulated noise we can achieve the global minimization, as explained below.

Non-convex search engine

Simulated annealing is a stochastic strategy for searching the ground state. A fast-simulated annealing (FSA) is a semi-local search and consists of occasional long jumps. The cooling schedule of FSA algorithm is inversely linear in time which is fast compared with the classical simulated annealing (CSA) which is strictly a local search and requires the cooling schedule to be inversely proportional to the logarithmic function of time. A general D dimensional Cauchy probability for generating the state is given. Proofs for both FSA and CSA are sketched. A double potential well is used to numerically illustrate both schemes.

Simulated annealing³

Szu and Hartley have shown in Phys Lett. and IEEE Proc. 1986, the Fast Simulated Annealing (FSA) approach, combining the increasing numbers of local Gaussian random walks at a high temperature T, with an unbounded Levy flightsat $<{\text{Δx}}^2{>}_{{\text{ρ}}_{\text{C}}}=\infty$ a low temperature in the combined Cauchy noise ${\text{ρ}}_{\text{C}}\left(\text{Δx}\right)={(1+{\frac{\text{Δx}}{\text{T}}}^2)}^{-1}=1-{\frac{\text{Δx}}{\text{T}}}^2+\dots .$ We proved a speed up cooling schedule at an inversely linear time step ${\text{T}}_{\text{C}}={\text{T}}_{\text{o}}/\left(1+\text{t}\right)$ This is much faster than that associated with Gaussian noise alone:${\text{ρ}}_{\text{G}}\left(\text{Δx}\right)=\exp \left(-{\frac{\text{Δx}}{\text{T}}}^2\right)\cong 1-{\frac{\text{Δx}}{\text{T}}}^2$ ,to be inversely logarithmic time step:${\text{T}}_{\text{G}}={\text{T}}_{\text{o}}/\left(1+\text{log}\left(1+\text{t}\right)\right)$ . This fact was proved by Geman and Geman² in 1984, used in 1985 by Sejnowski’s Boltzmann’s machine for Net-talk.

Cauchy machine

Y. Takefuj and Szu designed one per neuron, an electronic implementation of a set of stochastic Langevin equations with Cauchy additive noise ${\text{ρ}}_{\text{c}}\left(\text{x}\right)$ .

The set of Langevin dynamics enjoys the faster inversely linear cooling schedule. Optical version of a Cauchy machine is done by Kim Scheff and Joe Landa. The Cauchy noise is optically generated by the random reflection of the displacement x of the optical ray from a uniformly random spinning mirror angle $\text{θ}\left(-\frac{\text{π}}{2},\frac{\text{π}}{2}\right)$ . The temperature T is the distance parameter between the mirror and the plate. “Asymmetric key encryption uses a pair of mathematically related keys, each of which decrypts the encryption performed using the other. Some, but not all, of these algorithms have the additional property that one of the paired keys cannot be deduced from the other by any known method other than trial and error. An algorithm of this kind is known as a public key or asymmetric key system. Using such an algorithm, only one key pair is needed per user. By designating one key of the pair as private (always secret), and the other as public (often widely available), no secure channel is needed for key exchange. So long as the private key stays secret, the public key can be widely known for a very long time without compromising security, making it safe to reuse the same key pair indefinitely. (Ref: ethw.org/Cryptography)”. The simple table of hashing (copping to pieces) and reverse-hashing are quick you get what you pay for, is not safe.

We conclude with current rapidly development of AI computational intelligence. This may be due to the closely matched MPD Computers with Vector Matrix Python Algorithm without the inner do loops. This fact is like a software glove wearing a MPD five fingers hardware, they can operate from layer to layer moving forward without slow down. Moreover, there are un-limited training data existed in the Cloud to run through the closely matched software and hardware. Such a deep learning architecture and algorithm have revolutionized the computational intelligence. One wishes to learn how Massively Parallel and Distributed (MPD) computing power become "robust and fault tolerance" error free, because the storage memory of each state can be made orthogonal in the high dimensional linear vector space (Hilbert space). One would take each node as a trading partners, the horizontal supply chain as the layer of nodes, and the vertical demand chain as the layer by layer "back prop training algorithm" That's how machine learning can do the e-commerce business.

"AI ANN Deep Learning " etc. given by Google, Baidu, Facebook, etc. their Chief Scientists, Geoffrey Hinton, Andrew Ng, Yann LeCun, respectively. Lower dose talks will be their interview talks. e.g. Andrew Ng ask Geoffrey Hinton why AI becomes so hot now?

We itemize the reasons that we believe “Blockchain and Cryptocurrency” might work this decade when the main trustworthiness is overcome.

1. Technology has been matured: According to Stanford CS Professor Andrew Ng, the magic of massively parallel distributed (MPD) computing power is available, e.g. MPD Graphic Processor Units is reduced to a backplane augmented on PC. This hardware is matched “like glove with fingers” with massive parallel Vector-Matrix computer code(gloves), “deep learning” without the inner do-loops, e.g. Python language, as well as the enormous training data is available in the Cloud (e.g. “Coursera Inc.” offered by Prof. Ng).
2. Decentralized Internet of Business Notes “I owe you such and such with an explicit reneging condition” will be distributed to all members throughout the business community. (However, only the direct involved party has the private key can read the detail transaction). The reputation cannot be bankrupted and thus is at stake if is not followed.

Authors declare that there is no conflict of interest.

1. Metropolis N, Rosenbluth AW, Rosenbluth MN, et al. Equation of State Calculations by Fast Computing Machines. J Chem Phys.1953; 21(6):1087–1092.
2. Geman S, Geman D, IEEE Trans, Patt, Arian. Mach. Int., PAMI-6 (No. 6), 1984:721–741.
3. Szu HH, Hartley RL. Simulated Annealing with Cauchy Probability submitted to Physic Letter A, 1984.
4. Wikipedia RSA Coding and Decoding
5. JF Champollion, is virtually complete by the counting of the repetition in Greek and that of Egypt Hieroglyphic, e.g. Queen Cleopatra.
6. Yang Ji, Yunchul Chung, Sprinzak D, et al. An Electronic Mach-Zehnder Interferometer. Nature. 422:415–418.

Dr. Szu has been a champion of human brain sciences and brain-style computing for 3 decades; a founder, former president, and governor of International Neural Network Society (INNS), he received the INNS D. Gabor Award in 1997 “for pioneer implementations of fast simulated annealing search,” and the Eduardo R. Caianiello Award in 1999 from the Italy Academy for “elucidating chaotic neural net as fuzzy logic membership function.” Recently, he contributed to the unsupervised learning of the thermodynamic free energy of sensory pair for fusion. Because of this contribution, Dr. Szu is elected as a foreign academician of Russian Academy of Nonlinear Sciences in 1999. Recently, SPIE awarded him with the Nanoengineering Award and the Biomedical Wellness Engineering Award. Besides 640 publications, over dozen US patents, Dr. Szu taught students “how to be creative” according to the Boltzmann, Ehrenfest, Uhlenbeck’s Reinsurance Individual and Team Creativity Methodology. He received in 1971 PhD in Physics. He proved the Einstein diffusion fluctuation-dissipation relationship for all mediums of arbitrary mean free paths, using the stochastic version of the Boltzmann integral-differential transport equation. (His thesis advisor is Prof. George Uhlenbeck at the Rockefeller University, New York, NY) He worked at Naval Research Lab in Washington DC over 15 years (1977-1990). He began at GS-12 in Plasma Physics Div. and produced US patents of heavy ion isochronously cyclotron and tunable free electron infrared laser; promoted to GS-13 in Optics Div.; promoted to GS-14 in Electronics Warfare Div., he developed fast search Cauchy machine; he was promoted as GM-15 and led the Information Science Group, leader of Naval Surface Warfare Center at White Oak (1990-1996) and relocated to Dahlgren, VA (1997-2008). He became senior scientist at Army Night Vision Electronic Sensor Director, Ft. Belvoir, VA. He has been a visiting member of Institute for Advanced Studies at Princeton in 1977-78, on leave to Ala Marta NCKU created 3C Center. Prof. Szu has been appointed as Research ordinary Professor of CUA Fellow of American. Institute Medicine and BioEngineering 2004 for breast cancer passive spectrogram diagnoses; Fellow of IEEE (1997) for bi-sensor fusion; Foreign Academician, Russian Academy of Nonlinear Sciences, 1999, for unsupervised learning; Fellow of Optical Society America (1996) for adaptive wavelet; Fellow of International Optical Engineering (SPIE since 1995) for neural nets; Fellow of INNS (2010) for a founding governor and former president of INNS

Dalila Benachenhou is born in Nigeria Africa. She has earned a Ph. D. in the Statistics Department of American University. She has been working at World Bank as Intern and Contractor. She is a Research Professor at George Washington University at Washington DC.

Masud Cader serves as the Lead of Country Analytics for the International Finance Corporation, the private sector arm of the World Bank Group. In this position Masud is responsible for strategy integration of large cross-country initiatives such as One Belt One Road and applying analytics to create novel insights that link development strategy with private sector client implementation. Masud also co-heads the World Bank Group-IMF Economic Networks practice. He has over 20 years of experience in corporate finance, sustainable investing, investment management, equity and credit portfolio management, trading, and use of artificial intelligence to manage difficult development problems. Masud has degrees from Purdue University, American University, and Johns Hopkins University. He also teaches research courses at Georgetown University, McDonough School of Business.