
Review Article Volume 1 Issue 1
Kernel machine to doing logic programming in Hopfield network for solve non horn problem-3sat
Shehab Abdulhabib Saeed Alzaeemi,
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Saratha Sathasivam, Salaudeen Abdulwaheed Adebayo, Mohd Shareduwan M Kasihmuddin, Mohd Asyraf Mansor
School of Mathematical Sciences, Universiti Sains, Malaysia
Correspondence: Shehab Abdulhabib Saeed Alzaeemi, School of Mathematical Sciences, Universiti Sains, Malaysia
Received: July 03, 2017 | Published: April 28, 2017
Citation: Alzaeemi SAS, Sathasivam S, Adebayo SA, et al. Kernel machine to doing logic programming in Hopfield network for solve non horn problem-3sat. MOJ App Bio Biomech. 2017;1(1):1–6. DOI: 10.15406/mojabb.2017.01.00001
Download PDF
Abstract
Kernel machine is computationally efficient and has the capability to function on high dimensional analysis data with random complex structure. The aim of this research is to provide a new insight on the kernel machines integrated with Hopfield Network in doing logic programming (KHNN). The newly proposed method emphasized on non horn clauses logic. Kernel machine reduced the computational burden by intelligently define the embedded memory pattern in high dimensional feature space. Since KHNN is able to formulate the estimation of neuron states efficiently, computation in high dimensional feature space of the network can be reducing dramatically. The simulation of KHNN will be executed by using Dev C++ software. The robustness of KHNN in doing non horn clause 3 sat will be evaluated based on global minima ratio, root mean square error (RMSE), and sum of squared error (SSE), mean absolute error (MAE), mean percentage error (MAPE) and computation time. The result obtained from the computer simulation demonstrates the effectiveness of KHNN in doing non horn clause problem-3 sat.
Keywords: linear kernel machine, logic programming, non-horn clause
Introduction
A neural network which is recognized as artificial neural network is a mathematical model or computational model that tries to simulate the structure and functional aspect of biological neural networks. It can solve complicated recognition solve optimization problems and analysis problems. It is because it composed of huge amount of interconnected neurons to solve specific problems.1 Hopfield Network is a recurrent neural network investigated by John Hopfield in the early 1980s. Hopfield network serves as a content-addressable memory system with binary threshold units.2 Logic is deals with false and true while in the logic programming, a set of Non Horn clauses 3 sat that formed by atoms are represented to find the truth values of the atoms in the set. It is using neurons to store the truth value of atoms to write a cost function for minimization when all the clauses are satisfied.3 Moreover, a bi-directional mapping between propositional logic formulas and energy functions of symmetric neural networks had defined by Gadi Pinkas4 and Wan Abdullah.5 Further detail can refer to the references. The advantages by using Wan Abdullah’s method are it can revolves around propositional non Horn clauses 3 sat and learning ability of the Hopfield network and hunts for the best solutions, given the clauses in the logic program, and the corresponding solutions may change as new clauses added. This research focus in kernel Hopfield neuron network, Kernel machine are powerful, computational effective analytical tools that are qualified for working on high dimensional data with complex structure.6 In kernel methods, the data are mapped from their original space to a higher dimensional feature space.7 Any operation, that can be represented through dot products has a kernel evaluation and called kernelization.8,9
The rest of the paper is organized as follows
Section II Linear Kernel Machine, In section III Kernel Hopfield Neural Network, IV Logic Programming in Kernel Hopfield Neural Network, V Simulation and discussion and section VI to conclude the study.
Linear kernel machine
In their study Kernel Methods in Machine Learning,10 Suppose we are given empirical data:
(1)
Here, the domain
is some nonempty set that the inputs (predictor variables)
are taken from; the
are called targets (the response variable). Here and below,
where we use the notation
. Note that we have not made any assumptions on the domain
other than it being a set. In order to study the problem of learning, we need additional structure. In learning, we want to be able to generalize to unseen data points. In the case of binary pattern recognition, given some new input
, we want to predict the corresponding
(more complex output domains
will be treated below). Loosely speaking, we want to choose
such that
is in some sense similar to the training examples. To this end, we need similarity measures in
and in {±1}. The latter is easier, as two target values can only be identical or different. For the former, were quires a function?
(2)
(Figure 1) A simple geometric classification algorithm: given two classes of points (depicted by “o” and “+”), compute their means
and assign a test input
to the one whose mean is closer. This can be done by looking at the dot product between
[where
] and
which changes sign as the enclosed angle passes through
. Note that the corresponding decision boundary is a hyper plane (the dotted line) orthogonal to w.10 Satisfying, for all:
(3)
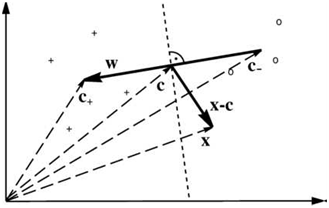
Figure 1 Kernel Methods in Machine Learning.
where
maps into some dot product space
, sometimes called the feature space. The similarity measure
is usually called a kernel, and
is called its feature map. The advantage of using such a kernel as a similarity measure is that it allows us to construct algorithms in dot product spaces. It is interesting to note that the above optimization problem can be entirely formulated in terms of dot products hence it can be solved in an arbitrary feature space induced by a kernel function. That is the kernel represents a dot product on a different space
called feature space into which the original vectors are mapped. With the introduction of a suitable kernel function the above learning procedure of the Adatron can be carried out in an arbitrary feature space where on the one hand the linear separability of the problem be guaranteed for every processing unit and on the other, the high dimensionality of the feature space produces an increment on the capacity of the network. In this way a kernel function defines an embedding of memory patterns into (high or infinite dimensional) feature vectors and allows the algorithm to be carried out in feature space without the need of representing it explicitly. With the introduction of a suitable kernel function the working of the network is mapped into a high dimensional feature space with the consequence that the capacity of the network is increased where
is the kernel function and the
are the Lagrange multipliers equal to 1.
In this study we will use kernels are the linear, shown in relation (4). The linear kernel is the simple dot product in input space whereas the other kernel functions represent dot products in arbitrary feature space.11
The linear kernel is
(4)
Kernel Machine technique is used as it can solve the combinatorial optimization problems that always occur in Hopfield network, also can reduce parameter processing time and sensors for robots.12
Kernel hopfield neural network
In kernel methods, the data are mapped from their original space to a higher dimensional feature space. The basic idea behind the kernel machine is that under certain conditions the kernel function can be interpreted as an inner product in a high dimensional feature space.13,14
A linear kernel helps us to do calculation faster which would involve computations in higher dimensional space, also to induce a configuration of synaptic weights that maximize the stability of the processing unit.
Expression the updating rule in Hopfield neural network can be written:
(5)
There local field is given by the equation below
(6)
then
(7)
to obtain the dual representation of the local field of the HNN in feature space which can be written as:
(8)
Nevertheless rewriting the definitions (4) of the kernel functions in terms of the products of components of the involved vectors in input space an expression equivalent to (3) for the weight vectors can be given as a generalized product of functions of the memory components. It is shown in (8) that for the linear kernel this is readily done. As an example let us consider a simple the linear kernel when
Equation (7) can be written
(9)
(10)
Also
(11)
Inserting (9) to (11)
(12)
Or can write that:
(13)
From the above derivation it can be seen that the right hand side expression of (13) is a generalized inner product of the functions of the components of vectors S all the neuron’s final state for the local minima that stored and Y is a learned interpretation stored in CAM. In conclusion the kernel machine allows a straight reroute generalization of the Hopfield network to a higher dimensional feature space. The important advantage of this procedure is that in principle all processing units can be trained to optimal stability.
Logic programming in kernel hopfield neural
network
Kernel Hopfield neural network is a numerical procedure to minimize energy function to find membership grade. We will lead the way in using the neural network to solve optimization problems. It is a well-known technique used based on Lyapunov energy function and it is useful for solving combinatorial optimization problems as a content addressable memory or an analog computer. Combinatorial optimization consists of looking for the combination of choices from a discrete set which produces an optimum value for some related cost function. Use Kernel Hopfield network that can handle non-monotonicity of logic to model and solve combinatorial optimization problems.15 Kernel Hopfield neural network algorithm revolves around propositional non-Horn clauses and learning the ability of the Hopfield network.
Khnn-Non-Horn Clauses 3sat algorithm is as followed
- Given a logic program, translate all Non- Horn clauses in the logic program into basic Boolean algebraic form:
(18)
2. Identify a neuron to each ground neuron.
3. Initialize all synaptic weight to zero.
4. Derive a cost function that is associated with the negation of all the clauses, such that
represents the logical value of a neuron x, where
is the state of neuron corresponding to x,
. Negation (neuron x does not occur) is represented by
; A conjunction logical connective is represented by multiplication whereas a disjunction connective is represented by addition.
5. Compute the synaptic weights by comparing cost function
with energy function
(wan Abdullah's method).
6. Training by checking clauses satisfaction of non-horn clauses by applying artificial bee colony and exhaustive search method. Satisfied assignment will be fed to the Hopfield network as CAM as
. If the network met the inconsistencies, the network will reset the search space (by using Wan Abdullah method).
7. We implemented Sathasivam's relaxation technique to ensure the network relaxed to achieve final state (Find the final state of the neurons, if the state of the neurons remains unchanged after five loops, we consider it as stable state). Hence, the information exchange between neurons will be updated based on the following equation: (19)
Where R denotes the relaxation rate and
refers to the local field of the network.(Neuron relaxation).
8. Randomize the states of the neurons.
9. Find the corresponding local field by using the following equation
(20)
10. Classify the final state of the neurons by using Hyperbolic Activation Function
(21)
Where
(22)
11. Calculate the final energy by using the following equation
(23)
If
else
12. Extract all the neuron’s final state for the local minima. Store it at
.
13. Calculate the corresponding kernel function by using the following equation
(24)
Where Y is a learned interpretation stored in CAM.
14. Find the corresponding kernelized local field by using the following equation
(25)
15. Classify the final state of the neurons by using Hyperbolic Activation Function
(26)
Where
(27)
16. Calculate the kernelized final energy by using the following equation
(28)
If
else
17. Find the corresponding MSE, RMSE, SSE, MBE, MAPE, SMAPE, Global minima ratio, CPU time.
Simulation and discussion in linear kernel hopfield
neural network
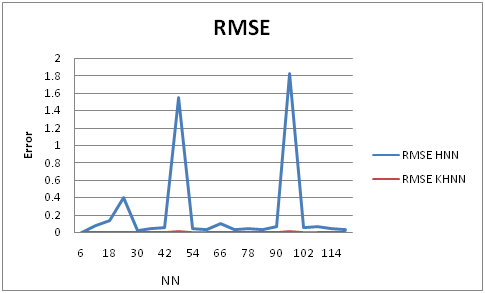
In order to obtain the results, computer simulations have been tested using Microsoft Visual Dev C++ 2015 Express for Windows 7 to demonstrate the ability of the kernel machine in doing the logic programs for a Hopfield network based on Wan Abdullah’s method to solve non-horn clauses problems. The number and the order of the clauses are chosen by the user using try and error technique.16 The numbers of neurons involved are increased in each training. The maximum number of neurons is 120 to find the corresponding RMSE, MAE, SSE, MBE, MAPE, SMAPE, Global minima ratio, CPU time. The relaxation was run for 100 trials and 100 combinations of neurons so as to reduce statistical error. The selected tolerance value is 0.001. All these values are obtained by try and error technique, where several values are tried as tolerance values, and the value which gives better performance than other values are selected. The comparison between Hopfield neural network and linear kernel Hopfield neural network. From (Figures 2-7) as presented above represent the performance comparison of the errors for both Hopfield neural network and Linear Kernel Hopfield neural network. noted when the NN are increasing, the errors to be increasing due to the model become more complicated because there are several local minima are trying to stuck. During the kernel machine prevents that from happening we see the errors equals to zero because the kernel machine does harmony between the data and the model of the Hopfield. The results from the (Figure 8), showed that the ratio of global solutions with different number of neurons (NN=6 to NN=120) for KHNN-Non-Horn Clauses SAT and HNN-Non-Horn Clauses 3SAT. It is clear from figure 8 that the global minimum ratio of KHNN-Non-Horn Clauses 3SAT closer to one compared HNN-Non-Horn Clause 3SAT. The kernel machine shows that the global solutions obtained are nearly or 1 for all values of NN, even though the network become more complex by increasing the NN, this does not affect the results significantly. However, the results of global minima ratio obtained, for kernel machine is more stable and consistent even as NN increases. From the (Figure 9) we compare computation time of Hopfield neural network with Kernel machine and computation time of Hopfield neural network without Kernel machine, it was observed that as NN increase, the running time of KHNN's method better from HNN's method. In addition, the difference in the computational time between KHNN's method and HNN’s method turn out to be more visible as the network complexity increase. These results justify consistency and stability of Hopfield neural network with Kernel machine since they are less susceptible to get stuck at the local minima as compared to Hopfield neural network without Kernel machine.17-19
Conclusion
The research utilized the linear kernel (KHNN) in finding optimal neuron states, which portrayed an improved method of doing logic programming in Hopfield network. The performances of these two methods KHNN and HNN were compared based on RMSE, MAE, SSE, MBE, MAPE, SMAPE, Global minima ratio, CPU time. Results obtained indicate that the KHNN improved the efficiency in finding global solutions. Besides, the computational time using KHNN is better than the HNN. Furthermore, this poses an indication that KHNN is well adapted to a complex network compared to HNN, whose effect is obviously seen as the complexity of the network increases simply increases the number of neuron (NN). The results obtained also certified that KHNN always converges to the optimal solution or nearly to the optimal solutions and maintains the population of the candidate solutions for the problem to be solved. In addition to this, KHNN is less prone to get trapped in the local optima or in any sub-optimal solutions. In contrast, HNN exhibits slow convergence to the desired solutions (global solutions) and takes longer computational time as the network gets larger and complex. Thus, from the simulation results obtained, it can be concluded that KHNN is a promising machine for solving optimization problems and is a useful technique when dealing with a large and complex search space, while the results of the errors of RMSE, MAE, SSE, MBE, MAPE, SMAPE to zero in KHNN strengthening the assertion of global solutions in the process.
Acknowledgements
Conflict of interest
Author declares that there is no conflict of interest.
References
- Sathasivam, Saratha, Muraly Velavan. Boltzmann Machine and Hyperbolic Activation Function in Higher Order Network. Modern Applied Science. 2014;8(3):140‒146.
- Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci USA. 1982;79(8):2554‒2558.
- Sathasivam S, Wan Abdullah. The Satisfiabilty Aspect of Logic on Little Hopfield Network. American Journal of Scientific Research. 2010;7:90‒105.
- Pinkas G. Energy Minimization and the Satisfiability of Propositional Calculus. Neural Computation. 1991;3:282‒291.
- Wan Abdullah WAT. Neural Network logic. In: Benhar O, editors. Neural Networks: From Biology to High Energy Physics. Pisa, Italy: ETS Editrice; 1991. 135‒142.
- Rosipal R, Girolami M, Treja LJ. On Kernel Principal Component Regression with covariance inflation criterion for model selection. UK: Technical report; 2001.
- Kobayashi K, Komaki, F. Information Criteria for Kernel Machines. Japan: Technical report; 2005.
- Demyanov S, Bailey J, Ramamohanarao K, et al. AIC and BIC based approaches for SVM parameter value estimation with RBF kernels. JMLR Proceedings. 2012;25:97‒112.
- Zhang R. Model selection techniques for kernel-based regression analysis using information complexity measure and genetic algorithms. 2007:1‒133.
- Hofmann Thomas, Bernhard Schölkopf, Alexander J, et al. Kernel methods in machine learning. The annals of statistics. 2008;36(3):1171‒1220.
- Schölkopf, Bernhard, Alexander J, et al. Learning with kernels: support vector machines, regularization, optimization, and beyond. 1st ed. USA: The MIT Press; 2002. 644.
- Moreno, José Alí, and Cristina García. Robot Path Planning in Kernel Space. International Conference on Adaptive and Natural Computing Algorithms. 2007;667‒675.
- García Cristina, José Alí Moreno. The hopfield associative memory network: Improving performance with the kernel trick. Ibero-American Conference on Artificial Intelligence. 2004;871‒880.
- García Cristina, José Alí Moreno. The kernel hopfield memory network. International Conference on Cellular Automata. 2004:755‒764.
- Leslie C, Eskin E, Noble WS. The spectrum kernel: A string kernel for SVM protein classification. Pac Symp Biocomput. 2002;7(7):564‒575.
- Sathasivam S. Application of Neural Networks in predictive data mining. Proceeding of 2nd International Conference on Business and Economic Research. 2011.
- Scholkopf B, Smola A. Learning with Kernels. USA: MIT Press; 2002. p. 1‒33.
- Horn Alfred. On sentences which are true of direct unions of algebras. The Journal of Symbolic Logic. 1951;16(1):14‒21.
- Sathasivam Saratha, Wan Ahmad Tajuddin Wan Abdullah. Logic mining in neural network: reverse analysis method. Computing. 2011;91(2):119‒133.

©2017 Alzaeemi, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


