Borchers classical remarks raise important aspects of the second law of classical thermodynamics considering temperature as an integrating denominator as well as using thermal and mechanical variables classes by an innovative structural-based statement for the first law of thermodynamics.¹ However, he advised seriously that his remarks need to be discussed using other approaches to entropy, and some further remarks will be very useful. Of course, the possibility of applying Borchers approach on the other entropy definitions is involved in various mathematical and physical challenges, and cannot be applied on a wide ranges of them, for example Boltzmann entropy equation. Now, due to our current knowledge on entropy, it is time that his approach and remarks be studied and developed using more general point of views of entropy. In fact, in order to study more on the basic foundations of them as well as getting closer to their standard form, it is necessary to generalize the basis of these equations based on more advanced approaches on entropy. Due to Borchers use of the classical definition of entropy to formulate his equations, he needed to base the equations on internal energy. By using other definitions of entropy, Borchers approach can be extended based on heat transfer and mechanical variables classes that can be directly measured. In this paper, using an innovative separation to the general classes of the Borchers variables, and considering Borchers thermo-dynamical system as well as due to the featured aspects of the Boltzmann entropy equation, the second law is studied using Borchers classical perspective as well as the quasi-statistical equation of entropy with a common base as Boltzmann entropy equation as well as structure-based properties as Borchers statement of the first law of thermodynamics. Finally, some further remarks are extracted and discussed.

Keywords: second law of thermodynamics, borchers remarks, statistical approach, thermal variables classes, mechanical variables classes

Borchers remarks on the second law show that in addition to establishing the Clausius inequality, it is necessary to establish some equations on the mechanical and thermal variables classes.¹ Considering a structural-based statement of the first law of thermodynamics, his remarks are based on the supposition of temperature as an integrating denominator as well as using thermal and mechanical variables classes. Borchers statement of the first law of thermodynamics is:

$dU= \delta Q- {\displaystyle \sum {\zeta }_i}d{x}_i$ , (1)

Where ${\zeta }_{\text{i}}$  and  are mechanical variables classes, and $\delta \text{Q}$ is the heat exchange. So, Eq.1 is not energy conservation principle only, rather is dependent on the structure of the system as well as some properties of the performed process. Two main of the Borchers remarks are:

$\frac{\partial }{\partial {\text{x}}_{\text{i}}}\left(\frac{1}{\text{T}}\frac{\partial \text{U}}{\partial \text{y}}\right)=\frac{\partial }{\partial \text{y}} \frac{1}{\text{T}}\left( {\zeta }_{\text{i}}+\frac{\partial \text{U}}{\partial {\text{x}}_{\text{i}}} \right)$

$\frac{\partial }{\partial {\text{x}}_{\text{i}}} \frac{1}{\text{T}} \left( {\zeta }_{\text{j}}+ \frac{\partial \text{U}}{\partial {\text{x}}_{\text{j}}} \right)=\frac{\partial }{\partial {\text{x}}_{\text{j}}} \frac{1}{\text{T}} \left( {\zeta }_{\text{i}}+ \frac{\partial \text{U}}{\partial {\text{x}}_{\text{i}}} \right)$ , (2)

That ${\text{x}}_{\text{i}}$ , ${\zeta }_i$  are mechanical variables, is extra coordinate to describe the thermal properties of the system,$\text{U}$ is internal energy, and $\text{T}$ is temperature. In order to apply Borchers approach on other entropy definitions, we face different mathematical and physical challenges. However, he seriously advised that his approach can be developed, and some further remarks can be extracted that will be very useful.¹ Borchers showed that although the second law of classical thermodynamics has been established for heat exchange of energy, due to the Borechers statement of the first law of thermodynamics, the equations governing the mechanical variables as well as the mechanical behavior of the system in general are equivalent to that. Therefore, inspired of Borchers remarks as well as more general approaches to entropy, it is expected that the proofs of mechanical behavior are also available in the second law. In this regard, it is necessary to take advantage of other relevant perspectives in order to study the issue. Now, using other exiting definitions of entropy as well as our current knowledge on entropy, it is time that his approach be studied and developed. So, in the evolution and effort to clarify of the second law, it is possible to express it in terms of variables that can be directly measured, and also to consider as much as possible the effective parameters in the analysis of thermodynamic processes. In fact, one of the main philosophies of the development and expansion of unified theories is to remove the ambiguities related to the classical expression of the second law of thermodynamics.^2–5 In nature, we generally encounter physical/thermodynamic processes and not perfect thermodynamic cycles. The definition of thermal entropy cannot provide the necessary conditions to consider other effective variables, in addition to thermal variables, in the study of physical processes. Also, expressing the second law in the form of an inequality as well as classical definition of entropy may give the result that the effects of various factors are not taken into account, and the classical entropy definition tries to provide the governing condition by considering the heat energy exchange. Given our current knowledge of more advanced systems,^6–11 other cases can be considered in the definition of entropy. Among these can be the transfer of energy in a way other than heat, as that is considered in MTD analysis. So, it is obvious that the expression of the second law in its inequality form is one of the main sources of related challenges, and it also somehow indicates that only the thermal factor has been taken into account and the attempt is made to consider the effects of other factors as an inequality. Entropy as a vague concept has always been discussed and many definitions as well as interpretations have been extended for it.^8–11 The structure of the second law in Carnot's approach includes heat exchange as a type of energy transfer between the system and the surrounding at the current temperature of the system. According to this case, entropy is defined and used to express the second law. However, Boltzmann studied entropy with a different attitude.^12–18 In statistical physics, Boltzmann calculated entropy in terms of accessible states for the statistical mechanics system. Therefore, the interpretation of the second law is only related to statistical concepts, which is an extraordinary development in the subject of knowing entropy. But there are still many unknowns about entropy. In fact, there have always been challenges to the classical form of the second law. Boltzmann entropy equation, based on the basis of statistical physics, obtains the general entropy equation, which has a special place in applications related to statistical systems. But it is not possible to apply Borchers approach and use his statement for the first law of thermodynamics directly to Boltzmann entropy equation. In this paper, in order to study entropy in terms of mechanical and thermal variables classes, using an innovative separation to the general classes of the Borchers variables, the quasi-statistical approach to entropy, which has a common basis as Boltzmann entropy equation, is used by considering Borchers variables as well as using Borchers approach to extract new remarks on the second law.

An acceptable entropy equation must establish the general properties are discussed in reference.¹³ Considering the highlights of Boltzmann entropy equation in the field of understanding the concept of entropy from the general point of view of statistical physics, in this paper, Borchers thermo-dynamical system is considered and his approach is studied to apply on this equation. Due to the fact that Borchers approach is formulated based on the classes of mechanical and thermal variables, it is not possible to directly apply it to Boltzmann entropy equation. So, it is necessary to use other perspectives related to this equation. In this paper, the quasi-statistical approach is used due to the fact that it is directly based on the variation classes of the activated energy components in the performed process. Therefore, considering quasi-statistical approach to entropy with the same base as Boltzmann entropy equation and structure-based properties as Borchers statement of the first law of thermodynamics:^{1,2,12–14,18}

$\delta s= k_{MS} \delta [ ln(W_{ u}) ]$   , (3)

That

${\text{W}}_{\text{u}}={\displaystyle \prod }_{\text{j}=1}^{\text{m}}{\text{w}}_{{\text{u}}_{\text{j}}}$

${\text{w}}_{{\text{u}}_{\text{j}}}$=${\dot{U}}_j$

$\delta U_j=\delta U_j-\delta U_j{}^{\text{'}}$  , (4)

Where ${\text{k}}_{\text{MS}}$ is a constant, and ${\text{u}}_{\text{j}},{\text{ u}}_{\text{j}}{}^{\text{'}}$  are dependent activated energy components in the general and quasi-statistical paths. So, considering Borchers statement of the first law of thermodynamics for any dependent activated energy component as well as by performing the required calculations on Burchers expression:

$\delta s= k_{MS} \delta [ln{\dot{U}}_1+ln{\dot{U}}_2+\mathrm{...}+ln{\dot{U}}_m]$

$= k_{MS}[\frac{\delta {\dot{U}}_1}{{\dot{U}}_1}+\frac{\delta {\dot{U}}_1}{{\dot{U}}_1}+\mathrm{...}+\frac{\delta {\dot{U}}_1}{{\dot{U}}_1}]$

$= k_{MS}[{\displaystyle \sum _{i=1}^m\frac{\delta {\dot{U}}_1}{{\dot{U}}_1}}]$

$= k_{MS}[{\displaystyle \sum _{i=1}^m\frac{\delta ({\dot{q}}_i+{\zeta }_i{\dot{x}}_i)}{({\dot{q}}_i+{\zeta }_i{\dot{x}}_i)}}]$  , (5)

Eq.5 takes entropy as an integrated relation of thermal and mechanical classes. Considering entropy as an integrating denominator, to apply Borchers approach on the Eq.5, an innovative solution is needed. According to the mathematical and physical properties of the classes of thermal and mechanical variables in Borchers view, a general class can be separated into classes of mechanical and thermal subspaces. In fact, the general paths performed by the system in the exchange of energy with the surrounding can always be achieved by two special processes in one of which only mechanical variables are activated and in the other only thermal variables appear in the path (Figure 1).

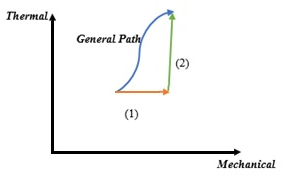
Figure 1 Separation of the general path into two mechanical and thermal paths.

$\delta s= k_{MS}[{\displaystyle \sum _{i=1}^m\frac{\delta ({\dot{q}}_i+{\zeta }_i{\dot{x}}_i)}{({\dot{q}}_i+{\zeta }_i{\dot{x}}_i)}}]$

$\equiv \delta s_{(1)}+\delta s_{(2)}$

$= k_{MS}{[{\displaystyle \sum _{i=1}^m{(\frac{\delta ({\dot{q}}_i)}{({\dot{q}}_i)})}_{1-2}+}{\displaystyle \sum _{i=1}^m(\frac{\delta ({\zeta }_i{\dot{x}}_i)}{({\zeta }_i{\dot{x}}_i)}})}_{1-2}]$

$= k_{MS}{[{\displaystyle \sum _{i=1}^m(\frac{\delta ({\dot{q}}_i)}{({\dot{q}}_i)}}+\frac{\delta ({\zeta }_i{\dot{x}}_i)}{({\zeta }_i{\dot{x}}_i)})}_{1-2}],$   (6)

$= k_{MS}{[{\displaystyle \sum _{i=1}^m(\frac{(\frac{\partial {\dot{q}}_i}{\partial y_i})}{{\dot{q}}_i}} \partial y_i + \frac{({\dot{x}}_i\frac{\partial {\zeta }_i}{\partial x_i} + {\zeta }_i\frac{\partial {\dot{x}}_i}{\partial x_i}+ \frac{\partial {\dot{q}}_i}{\partial x_i})}{{\zeta }_i{\dot{x}}_i}d{x}_i)}_{1-2}]$

Eq.6 has outstanding features in terms of mathematical structure and physical foundations, and it also provides the necessary conditions for development Borchers' point of view to Eq.5. In fact, considering that the mechanical part of the Eq.6 is activated only in path 1 and is not active in path 2, and also the thermal part is activated in path 2 and not active in path 1, the mathematical structure desired by Borchers can be applied on the mechanical and thermal parts of this equation. Finally, considering Eq.6 as well as Borchers approach to the required mathematical conditions for entropy:

$\frac{\partial }{\partial x_i}[\frac{(\frac{\partial {\dot{q}}_i}{\partial y_i})}{{\dot{q}}_i}]=\frac{\partial }{\partial y_i}[\frac{({\dot{x}}_i\frac{\partial {\zeta }_i}{\partial x_i} + {\zeta }_i\frac{\partial {\dot{x}}_i}{\partial x_i}+ \frac{\partial {\dot{q}}_i}{\partial x_i})}{({\zeta }_i{\dot{x}}_i)}],$   (7)

$\frac{\partial }{\partial x_j}[\frac{({\dot{x}}_i\frac{\partial {\zeta }_i}{\partial x_i} + {\zeta }_i\frac{\partial {\dot{x}}_i}{\partial x_i}+ \frac{\partial {\dot{q}}_i}{\partial x_i})}{({\zeta }_i{\dot{x}}_i)}]=\frac{\partial }{\partial x_i}[\frac{({\dot{x}}_j\frac{\partial {\zeta }_j}{\partial x_j} + {\zeta }_j\frac{\partial {\dot{x}}_j}{\partial x_j}+ \frac{\partial {\dot{q}}_j}{\partial x_j})}{({\zeta }_j{\dot{x}}_j)}],$   (8)

Eq.7 gives the general structure of the generalization of Borchers remarks based on the statistical approach to entropy. Mechanical and thermal classes are the basis of the physical structure governing the new remarks. According to the number of mechanical and thermal variables considered, the number of remarks extracted from Eq.7 is determined. Also, for the special Borchers case with only as required variables:

$\frac{\partial }{\partial x}[\frac{(\frac{\partial {\dot{q}}_i}{\partial y_i})}{{\dot{q}}_i}]=\frac{\partial }{\partial y}[\frac{({\dot{x}}_i\frac{\partial {\zeta }_i}{\partial x_i} + {\zeta }_i\frac{\partial {\dot{x}}_i}{\partial x_i}+ \frac{\partial {\dot{q}}_i}{\partial x_i})}{({\zeta }_i{\dot{x}}_i)}],$   (9)

Which is actually a direct development of Borchers remarks for the statistical perspective to entropy. The physics of this subject is very fundamental and actually provides a connecting line between classical thermodynamics and statistical thermodynamics. On this basis, it is necessary to pay special attention to these remarks in the analysis of statistical systems. In fact, calculations related to statistical systems need to establish new remarks. This allows system variables to maintain their classical structure while having their statistical nature.

The basic issues in this paper can be explained as an extension of Borchers classical view and remarks, combining Borchers classical view with a quasi-statistical approach with a common basis as Boltzmann entropy equation, as well as extracting further remarks in terms of heat exchange and work done in physical processes.

Remarks on the second law of thermodynamics have been developed from both experimental and theoretical aspects. In fact, studies on the different aspects of the second law have always been mentioned as a necessary issue in the physical theories. The development of various definitions for entropy can be one of the theoretical roots for the relevant remarks. According to the general characteristics that every definition of entropy must have, the issue of expanding the relevant concepts can be pursued while using other scientific laws and according to the first law of thermodynamics. Borchers classical innovative expression of the first law of thermodynamics considers the structural and behavioral aspects of the system with regard to the performed process. In fact, this statement becomes the basis for the formation and definition of the classes for the studied system in the space of mechanical and thermal change variables. The structure of Clausius expression of the second law, and also assuming the entropy as an integrating denominator along with Borchers expression of the first law of thermodynamics forms the basis of Borchers remarks in the classes of mechanical and thermal variables. Development of the Borchers view for other definitions of entropy is generally associated with many mathematical and physical challenges, and is not possible in most cases. However, as Borchers has emphasized, extending his remarks to other views of entropy can take valuable aspects of the second law.

One of the most important and valuable views regarding entropy is Boltzmann statistical view in statistical physics. Theoretically, Boltzmann view can be applied to all physical problems without restrictions. However, from a mathematical point of view, Borchers classical view cannot be extended to it. So, it is necessary to use the corresponding quasi-statistical equation with a common base with Boltzmann's point of view. In this way, considering that the quasi-statistical approach has fundamental commonalities with Borchers expression of the first law, considering the decomposition of the vector of variables in the general space classes into its components in the subspaces of mechanical and thermal variables, the necessary mathematical process can be followed.

Although the basis of Borchers view is based on the laws of classical thermodynamics, the generality governing one of its basic hypotheses, which is the integrating denominator of entropy, makes it possible to generalize it to other views on entropy. In this paper, Borchers process is used with an innovative solution about the decomposition of general variable classes and the related mathematical process is followed. The extracted remarks have the basis of statistical physics, and in fact, they are related to entropy in the perspective of statistical physics. These remarks are part of the requirements of the second law, and are written on the basis of heat transfer and work done in physical processes, and at the same time include Borchers mechanical and thermal variables. This issue leads to the expansion of Borchers variables by paying attention to the statistical foundations of entropy and the second law, and it is necessary to pay attention to the application of the second law.

According to the development of Borchers classical view for the statistical concept of entropy, as well as new remarks with classical and statistical physical foundations for mechanical and thermal classes, new remarks take new aspects of the second law in statistical physics systems. New concepts need to be of special attention in the study of statistical physics systems and can provide an outstanding solution to indirectly apply the effects of the second law on the system. Also, the solution of extracting new remarks can be followed for the fundamental concepts of quantum mechanics and the quantum aspects of Borchers view can also be studied. In fact, according to the connection line created between classical thermodynamics and statistical physics, a new solution is developed for the study of statistical effects according to the classical nature of mechanical and thermal classes in physical systems.

None.

None.

The authors declare that they there are no conflicts of interest.

1. Borchers H-J. Some remarks on the second law of thermodynamics. Rep Math Phys. 1958;22(1):29–48.
2. Yeh Hsu‐Chieh. Remark on the second law of thermodynamics. Am J Phys. 1984;52(8):720–723.
3. Brown Harvey R, Jos Uffink. The origins of time-asymmetry in thermodynamics: The minus first law. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 2001;32(4):525–538.
4. Srinivasan J. Sadi Carnot and the second law of thermodynamics. Resonance. 2001;6(11):42–48.
5. Rivas Ángel. Strong coupling thermodynamics of open quantum systems. Phys Rev Lett. 2020;124(16):160601.
6. Chen Long-Qing, Yuhong Zhao. From classical thermodynamics to phase-field method. Progress in Materials Science. 2022;124:100868.
7. Saridakis Emmanuel N, Spyros Basilakos. The generalized second law of thermodynamics with Barrow entropy. Eur Phys J C. 2021;81(7):644.
8. Neri Izaak. Second law of thermodynamics at stopping times. Phys Rev Lett. 2020;124(4):040601.
9. Nakazato Muka, Sosuke Ito. Geometrical aspects of entropy production in stochastic thermodynamics based on Wasserstein distance. Phys Rev Res. 2021;3(4):043093.
10. Sosnovskiy Leonid A, Sergei S Sherbakov. On the development of mechanothermodynamics as a new branch of physics. Entropy. 2019;21(12):1188.
11. Basaran Cemal. Introduction to unified mechanics theory with applications. Springer Nature. 2023.
12. Goldstein S, Lebowitz J L, Tumulka R, et al. Gibbs and Boltzmann entropy in classical and quantum mechanics. Statistical Mechanics and Scientific Explanation: Determinism, Indeterminism Laws Nature. 2020:519–581.
13. Wehrl Alfred. General properties of entropy. Rev Modern Phys. 1978;50(2):221.
14. Shahsavari Saeed, Mehran Moradi. A New Approach to the Energy Conservation Principle and Physical Systems. Ph.D. Thesis in Mechanical Engineering, Isfahan University of Technology. 2022.
15. Shahsavari Saeed, Mehran Moradi. A General Solution to the Different Formulations of the Second Law of Thermodynamics. J Adv Res Fluid Mech Therm Sci. 2021;82(2):61–71. ‏
16. Tsallis Constantino. Some comments on Boltzmann-Gibbs statistical mechanics. Chaos, Solitons & Fractals. 1995;6:539–559.
17. Goldstein S, Lebowitz JL. On the (Boltzmann) entropy of non-equilibrium systems. Physica D: Nonlinear Phenomena. 2004;193(1–4):53–66.
18. Shahsavari Saeed, Moradi M, Torkaman P, et al. A Quasi-Statistical Approach to the Boltzmann Entropy Equation Based on a Novel Energy Conservation Principle. J Adv Res Fluid Mech Therm Sci. 2023;101(2):99–110.