
Mini Review Volume 2 Issue 2
Fully submerged depth against ocean waves
Mohammad Moonesun,
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Yuriy Korol, Olha Korneliuk
National University of Shipbuilding, Ukraine
Correspondence: Mohammad Moonesun, National University of Shipbuilding, Nikolaiev, Ukraine
Received: October 28, 2017 | Published: March 26, 2018
Citation: Moonesun M, Korol Y, Korneliuk O. Fully submerged depth against ocean waves. MOJ App Bio Biomech. 2018;2(2):117–119. DOI: 10.15406/mojabb.2018.02.00052
Download PDF
Abstract
This paper evaluates the effective depth of waves on the submarine at the depth of water. At the depth called the "Wave Base" the wave effects become so small that motion is negligible. This paper aimed to recommend a safe depth for calm and stable motion of a submarine. Depth of
/2 could be considered as the absolutely calm depth but the depth of 0.1
could be recommended as an operational safe and approximately calm depth for submarines. For this study, a torpedo shaped submersible is analyzed in some depths accompanying by regular surface wave. By increasing the depth, the reduction of submarine motions is evaluated. The results of this research can be used for AUVs, research submersibles and naval submarines. This analysis is performed by CFD tools of Flow-3D (V.10) software based on solving the RANS equations and VOF method. In this study a torpedo shaped submersible (Persia110) is considered. The general form and dimensions of this model is shown in Figure 1. This model has 1 DOF, free to pitch. The model has a volume of 8.38 liter, total area of 0.36 m2 and weight of 8.38 kg and transverse moment of inertia (Iyy) of 1.3 kg.m2.This model is the same in several depth in CFD method and the same for validation experiment in towing tank marine laboratory.
Validation and verification
For validating the results of Flow-3D modeling, an experimental test has been performed on the model Persia-110 in the towing tank of Admiral Makarov University, which has 33(m) length, 2.5(m) width and 1.3(m) draft (Figure 2).
CFD analysis
The general configurations and dimensions of domain are shown in Figure 3. The length and width are 12 and 2.6 meters. Depth is 4 meters (3.5 for draft and 0.5 for freeboard). There boundary conditions are: Input: wave, Output: Specified pressure and other sides are symmetry. The model is situated in different depths of "h" according to (Figure 3A). There are two mesh block: one block for the total domain with coarse meshes and other block for fine meshes around the object body. The accuracy of the shape of body depends on the fine meshes (Figure 3B) (Figure 3C). For producing the wave, the input boundary condition is "Wave". Flow-3D can produce regular and irregular waves. The produced wave and the situation of object under the waves are shown in (Figure 3D). The reason of selecting each parameter is mentioned below.
-


(A) Test in the surface draft of 7 cm and speed of 1 m/s(B) CFD modeling in the same conditions of experiment
Figure 2Comparison of the results of the experiment and CFD method.
-

A. Dimensions of Domain (in meter)
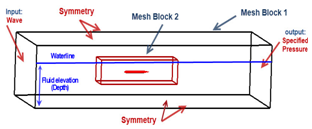
B. Boundary conditions in domain

C. Fine meshes in Mesh Block2
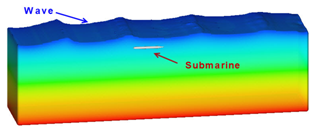
D. Generated wave and position of submarine
Figure 3 CFD modeling, (A) Dimensions of Domain (in meter), (B) Boundary conditions in domain, (C) Fine meshes in Mesh Block2, (D) Generated wave and position of submarin
Wave modeling
The defined Input boundary condition is regular wave. Here these parameters are defined in Flow-3D: wave amplitude 0.18 meters, wave period 1 second and mean fluid depth (according to the depth of domain) is 3.5 meters and current velocity is regarded zero. Based on these definitions, deep water condition is compatible because d/
>0.5. For deep waters according to the formula of
=1.56T2 the wave length is 1.56 meters. Wave speed according to C=
1.25 is 1.56 m/s. The orbital radius of wave articles path(R) according to this formula is depended on the distance from water surface (h): R=A.e-kh and k=2∏/
. Here can be stated as: 1). At the water surface, h=0 and R=A which means at the surface, the radius of orbital motion of articles equals to wave amplitude. 2) At h=
/2, there is R=0.043A. 3) At h=, there is R=0.002A. It is obvious that at the depth equal to /2, the circle radius is only 4% of the surface value and at the depth equal to , it is only 0.2% of the initial value at the surface. Therefore at the depths more than /2 the wave will be damped out.1–5
Considered conditions for analyses
For studying the wave effects on the submarine, several depth for submarine situation (h) are considered according to (Figure 3) (Table 1).
|
Submarine depth (m) |
Description (equivalent to) |
1 |
0 |
Body tangent to free surface |
2 |
0.05 |
Rs (or) 0.03
|
3 |
0.1 |
Ds (or) 0.06
|
4 |
0.15 |
1.5Ds (or) 0.09
|
5 |
0.25 |
2.5Ds (or) 0.16
|
6 |
0.35 |
3.5Ds (or) 0.22
|
7 |
0.55 |
5.5Ds (or) 0.35
|
8 |
0.75 |
7.5Ds (or) 0.48
|
9 |
0.95 |
9.5Ds (or) 0.61
|
10 |
1.6 |
@
|
11 |
2.4 |
@ 1.5
|
12 |
3 |
@ 3
|
Table 1 Considered conditions for analyses
Results
The time history of pith angle in 12 conditions is analyzed. Figure 4 shows two samples of time history for h=0.1 and 0.35 meter. Table 1 represents the results for each depth. The percentage of decrease in last column is based on comparison to h=0 therefore; average=((h0-hi)/h0*100). It should be notified that the static pitch angle of this submarine is 0.34 degree.6–10
-
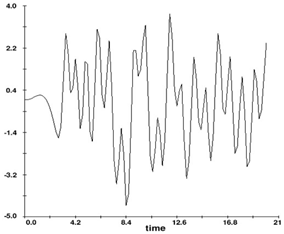
(A) h=0.1 , RMS=1.67 deg

(B) h=0.35 , RMS=1.22 deg
Figure 4 Time history of pith angle (A) h=0.1, RMS=1.67 deg, (B) h=0.35 , RMS=1.22 deg .
Conclusion
In conclusion, the results could be abstracted in the Figure 5 which fairly shows the gradient of motions versus depth of submergence. Depth of /2 could be considered as the absolutely calm depth but the depth of 0.1 could be recommended as an operational safe and approximately calm depth for submarines.
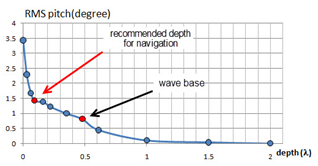
Figure 5Gradient of RMS pitch versus submergence depth of submarine.
Acknowledgement
Conflict of interests
The authors declare that there is no conflict of interest.
References
- Thurman, Harold V, Trujillo, et al. Essentials of Oceanography. 5th ed, USA: Prentice Hall; 2001:240–243.
- Dean WR. On the Reflexion of Surface Waves by a Submerged Circular Cylinder. Proc Camb Phil Soc. 1948;44(4):483–491.
- Ursell F. Surface Waves in the Presence of a Submerged Circular Cylinder, I and II. Proc Camb Phil Soc. 1949;46(1):141–158.
- Ogilvie TF. First–and Second–Order Forces on a Cylinder Submerged Under a Free Surface. J Fluid Mech. 1963;16(3):451–472.
- Chaplin JR. Nonlinear Forces on a Horizontal Cylinder Beneath Waves. J Fluid Mech. 1984;147:449–464.
- Etienne Guerber, Michel Benoit, Stéphan T Grilli, et al. Modeling of Fully Nonlinear Wave Interactions with Moving Submerged Structures. Proceedings of the Twentieth (2010) International Offshore and Polar Engineering Conference Beijing, China, 2010;529–536.
- Wu GX. Hydrodynamic Forces on a Submerged Circular Cylinder Undergoing Large–amplitude Motion. J Fluid Mech. 1993;254(1):41–58.
- Evans DV, Jeffrey DC, Salter SH, et al. Submerged Cylinder Wave Energy Device: theory and experiment. Applied Ocean Research. 1979;1(1):3–12.
- Dessi D, Carcaterra A, Diodati G, et al. Experimental investigation versus numerical simulation of the dynamic response of a moored floating structure to waves. Proceedings of the Institution of Mechanical Engineer Part M: Journal of Engineering for the Maritime Environment. 2004;218(3):153–165.
- Salter SH, Taylor JRM, Caldwell NJ, et al. Power conversion mechanisms for wave energy. Proceedings of the Institution of Mechanical Engineers Part M: Journal of Engineering for the Maritime Environment. 2002;216(1):1–27.

©2018 Moonesun, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.






