Of concern in the paper is a theoretical study of the effect of ventricular structure and mechanics on left ventricular aneurysm. A mathematical model has been developed by considering the left ventricle as an ellipsoidal shell. The structural non-homogeneity of the ventricle has been taken into account by considering the three distinct layers that exist in the left ventricle. The study pertains to an early stage of formation of the aneurysm (bulging), when the damage area is not too large. In view of this,it is assumed that the ellipsoidal geometry of the left ventricle is preserved, even after the formation of the aneurysm and also that the volumes of the three individual muscle layers after infarction remain equal to the respective volumes before infarction. The theoretical study has been performed by employing suitable analytical methods. The derived analytical expressions have been computed, by taking appropriate values of different parameters involved in the study. The results have been validated in a proper way.

Keywords: ventricular aneurysm, myocardial infarction, ellipsoidal shell, bulge factors, tensile stresses

Left ventricular aneurysm (LVA) is known to be a serious health disorder. It has been the observation of clinicians that in most cases, aneurysms develop in the apex wall of left ventricle. The aneurysm can absorb a portion of left ventricular ejection,which may lead to heart failure. Formation of an aneurysm on a ventricular wall,as observed by clinicians,complicates the pathological state of transmural myocardial infarction . However, the hemodynamic factors that are responsible for aneurysmal bulging are not completely known. Bartel et al.¹ conducted a study by using a biomechanical model with a motivation of exploring the said factors.They concluded that heart rate, contractility and afterload are the principal factors that cause aneurysm and aneurysmal bulging.The study suggests that in a clinical setting, it should be possible to control the size of bulging through hemodynamic management.

Studies on the mechanical behaviour and mechanism of myocardial infarction are quite useful for analysing the genesis of aneurysms. Deformation of the ventricular wall after infarction involves different mechanical factors; the infarcted myocardium supports the intra ventricular pressure and the incompressibility of the muscle wall. The selection of candidates for coronary bypass surgery depends on the following factors:

1. Estimation of the infarct size and location as well as the effect of the intensity of the chamber pressure to continue the circulation during systole, and
2. Whether the size of the infarct is enough to cause an eventual aneurysm.

This information is quite useful for having an idea as to how the deformation changes the intra ventricular haemodynamic. They are also helpful for the proper treatment of aneurysmectomy.

The model offers the opportunity to study in a fairly simple way the influence of a number of relevant features connected to ventricular geometry and muscle contraction based as much as possible on current physiological knowledge. Such studies also make it possible to estimate the diastolic and systolic properties of the heart, the ventricles and muscle before and after interventions. Of course, this approach leads, in general, to relatively complex models with a number of parameters.

According to Huxley’s theory,² force generation by the sarcomeres in response to activations results from chemical interactions, which can be demonstrated by electron microscopy in skeletal

muscle. But structure of sarcomere in cardiac muscle is the same as the striated muscle. The sliding filament model of Huxley² has been extensively applied to muscle mechanics, since it satisfies the thermodynamic data of striated muscle reported by Hill.³ Van Den Broek and Van Den Broek⁴ improved the model of heart as a nested set of thick-walled truncated ellipsoid of revolution with nonuniform wall thickness. The shells contain muscle fibres which generate wall tension, from which ventricular pressure results. Fiber length and orientation per shell were taken to have different values.

The geometry of the left ventricle was idealized as a thick-walled circular cylinder and the myocardium was assumed to be composed of an incompressible homogeneous and isotropic material in an investigation undertaken by Moskowitz⁵ to explain the physiology underlying left ventricular diastolic phenomena. Different mathematical models for left ventricle were also tried in the past by several researchers to estimate the stresses in the left ventricular wall. Misra and Singh^6–10 carried out several studies relevant to the mechanics of the left ventricle in normal and pathological states. Some recent investigations of aneurysms in the left ventricle are given by.^11–13

The mechanical behaviour of aneurysm formed in an arterial wall was studied by Ren and Yuan.¹⁴ They predicted that the aneurysm may rupture if the stress at the arterial wall is greater than its strength. A theoretical study was performed by Misra and his collaborators¹⁵ for the study of the mechanics of carcinogenic human arteries. The study was motivated towards finding theoretical estimates of hemodynamic flow during electromagnetic hyperthermia. Misra et al.^16,17 also reported their results for two separate studies on blood flow in the micro-circulatory system, which bear the promise of important applications in the treatment of cardiovascular diseases.

In 2019, Sui et al.¹⁸ carried out a statistical analysis for 183 patients with left ventricular aneurysm (LVA). Based on their observations, they discussed the efficacy of three different clinical treatment methods, out of which they suggested that surgery is the best treatment option for the treatment of LVA. Based on another statistical study, Ohlow¹⁹ made some important observations on the characteristics of congenital left ventricular aneurysms. Discussion on different aspects of surgical treatment of left ventricular aneurysm was made in,^20–22 while impact of surgery on patients with LVA was discussed in.^23–25 It is important to note that Pasque²⁶ and Kramer et al.²⁷ while discussing about left ventricular aneurysm repair stressed upon the importance of application of mathematical modelling theory to validate the observations of clinical investigations in cardiac mechanics and cardiac surgery.

A finite element model was employed by Guccione et al.²⁸ to study the mechanism behind the mechanical dysfunction in the border zone of left ventricular aneurysm. The study shows that myocardial contractile dysfunction is more responsible for mechanical dysfunction in the said region of the aneurysm than the intensified wall stress developed there. The left ventricle with an infarcted wall was modelled as a spherical shell by Radhakrishnan et al.²⁹ to perform a mathematical analysis of ventricular aneurysm that develops due to infarcts of different sizes. Based on this analysis ventricular wall deformation and stress were calculated. The study shows that the innermost layer is affected most severely, where the stress developed is maximum. The extent of wall damage was obtained in terms of the angle of damage and percentage of damage of the ventricular wall.

However, in the studies mentioned above, for the sake of simplification, the left ventricle was modelled as a spherical shell and so the eccentricity of the left ventricle was not taken into account. However, it is well-known that the eccentricity of the left ventricle is non-zero. In order to account for the effect of eccentricity and structural non-homogeneity on left ventricular aneurysm, the present study has been carried out by developing a mathematical model, in which the left ventricle is considered as an ellipsoidal shell, consisting of three distinct layers. The mathematical analysis has been performed by employing suitable analytical techniques. The model and the results obtained therefrom have been duly validated by comparing the results of this investigation with those of previous studies available in the existing literature.

The Model

On the basis of the assumption of muscle incompressibility, the volumes of the three muscle layers may be taken to be the same before and after infarction. If the area of damage is not too large, the infarcted segments preserve the ellipsoidal form, of course, with different eccentricity after the development of the aneurysm.

As already mentioned, the left ventricle is modelled as a three layered ellipsoidal shell of revolution; the major and the minor semi-axes of the non-infarcted muscle layers are denoted by $\left(a1,b1\right)$  (at the inner boundary of superficial bulbospiral muscle), $\left(a2,b2\right)$ (at the inner boundary of deep bulbospiral muscle), $\left(a3,b3\right)$ (at the outer boundary of deep sinospiral muscle) and $\left(a4,b4\right)$ (at the outer boundary of superficial sinospiral muscle). A schematic diagram has been presented in Figure 1. The corresponding values for the infarcted layers are denoted by $\left(A1,B1\right)\left(A2,B2\right)\left(A3,B3\right) and \left(A4,B4\right)$  respectively. Observations of previous investigators indicate that the set of ellipsoidal shells before infarction are concentric and further that the ratio between the minor and major axes is approximetly 0.87 for all the layers. The non-uniform thickness varies according to the law of incompressibility. The infarcted layers have the same eccentricity but differ from non-infarcted layers. Let $e$  and $e_1$ are respectively the eccentricities of the non-infarcted and infarcted layers. The major and minor semi-axes of the three different infarcted layers are assumed to be $\left(A1,B1\right)\left(A2,B2\right)\left(A3,B3\right)$  and $\left(A4,B4\right)$ respectively.

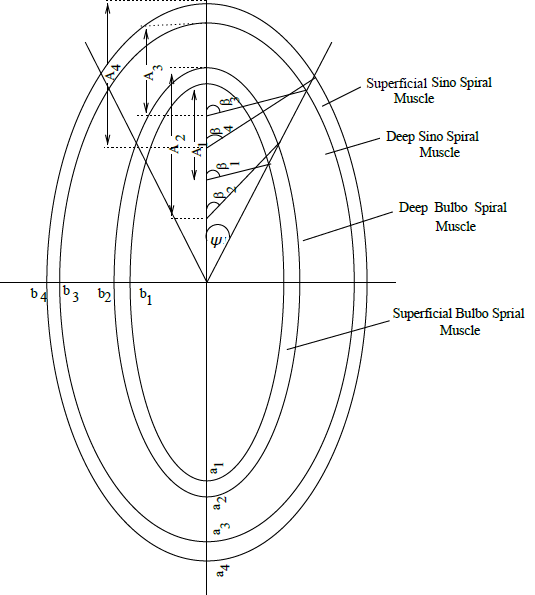
Figure 1 Schematic Representation of the Layered Ellipsoidal Structure of Left Ventricular Aneurysm.

Let $2\psi$ be the angle of damage; this is the angle made by the three concentric layers initially at their center and let the bulged segments subtend the angles $2{\beta }_{1}2{\beta }_{2}2{\beta }_3$ and $2{\beta }_4$ respectively at their centers.

The following assumptions will be made here.

1. The myocardial wall is composed of three layers viz. (i) superficial sinospiral muscle, (ii) deep sinospiral muscle and deep bulbospiral muscle and (iii) superficial bulbospiral muscle. The muscles are treated as incompressible material.
2. The two superficial layers remain unaffected but damaged deep layers are assumed to be replaced by an equivalent amount of fluid. This infarcted zone deforms into ellipsoidal caps, the outer and inner superficial layers are similar in all respects. Also the undamaged portion preserves the same shape.
3. The left ventricle is treated as a closed pressurized chamber loaded by intraventicular pressures at the instant prior to the opening of the aortic valve. The segment of the middle layer of the wall becomes infarcted at the apex. Thus the inner bulge of the infarcted zone is caused due to the resultant of intraventicular and fluid pressures, while the outer bulge supports the fluid pressure.
4. Mechanical behaviour of aneurysm is considered only at the instant prior to the opening of the aortic valve.
5. The length-tension relationship used as the contractile tension is a linear function of contracted length.
6. Necking is neglected near the edges of infarct.

Assuming that innermost segment of the pre-infarcted left ventricle is bounded by the part of the ellipsoidal shell whose major and minor semi-axes of the inner and outer boundaries are $\left(a1,b1\right)$  and $\left(a2,b2\right)$  respectively, as in,³⁰ calculations necessary for the present study have been performed. They are presented below.

Volumes before and after infarction

The predeformation volume of the innermost infarcted wall segment is given by

$V\left(innerlayer\right)=\pi \{\left(a_2{b}_2^3\right)[\frac{1}{b_2}-\frac{1}{3b_2}-\frac{cos\psi }{{(a_2^{2}si{n}^{{}^2}\psi +b_2^{2}co{s}^{{}^2}\psi )}^{{}^{\frac{1}{2}}}}$

$+\frac{b_2^2}{12}\frac{cos3\psi +3cos\psi }{{(a_2^{2}si{n}^2\psi +b_2^{2}co{s}^2\psi )}^{\frac{3}{2}}}\left]-\left(a_1{b}_1^3\right)\right[\frac{1}{b_1}-\frac{1}{3b_1}-\frac{cos\psi }{{(a_1^{2}si{n}^2\psi +b_1^{2}co{s}^2\psi )}^{\frac{1}{2}}}$

$+\frac{b_1^2}{12}\frac{cos3\psi +3cos\psi }{{(a_1^{2}si{n}^2\psi +b_1^{2}co{s}^2\psi )}^{\frac{3}{2}}}\left]+\frac{1}{3}\right[\frac{a_2^3{b}_2^{3}si{n}^2\psi cos\psi }{{(a_2^{2}si{n}^2\psi +b_2^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$-\frac{a_1^3{b}_1^{3}si{n}^2\psi cos\psi }{{(a_1^{2}si{n}^2\psi +b_1^{2}co{s}^2\psi )}^{\frac{3}{2}}}]\},$   (1)

$V\left(Middle\right)=\pi \{\left(a_3{b}_3^3\right)[\frac{1}{b_2}-\frac{1}{3b_3}-\frac{cos\psi }{{(a_3^{2}si{n}^2\psi +b_3^{2}co{s}^2\psi )}^{\frac{1}{2}}}$

$+\frac{b_3^2}{12}\frac{cos3\psi +3cos\psi }{{(a_3^{2}si{n}^2\psi +b_3^{2}co{s}^2\psi )}^{\frac{3}{2}}}\left]-\left(a_2{b}_2^3\right)\right[\frac{1}{b_2}-\frac{1}{3b_2}-\frac{cos\psi }{{(a_2^{2}si{n}^2\psi +b_2^{2}co{s}^2\psi )}^{\frac{1}{2}}}$

$+\frac{b_2^2}{12}\frac{cos3\psi +3cos\psi }{{(a_2^{2}si{n}^2\psi +b_2^{2}co{s}^2\psi )}^{\frac{3}{2}}}\left]+\frac{1}{3}\right[\frac{a_3^3{b}_3^{3}si{n}^2\psi cos\psi }{{(a_3^{2}si{n}^2\psi +b_3^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$-\frac{a_2^3{b}_2^{3}si{n}^2\psi cos\psi }{{(a_2^{2}si{n}^2\psi +b_2^{2}co{s}^2\psi )}^{\frac{3}{2}}}]\}$   (2)

 and

$V\left(Outer\right)=\pi \{\left(a_4{b}_4^3\right)[\frac{1}{b_4}-\frac{1}{3b_4}-\frac{cos\psi }{{(a_4^{2}si{n}^2\psi +b_4^{2}co{s}^2\psi )}^{\frac{1}{2}}}$

$+\frac{b_4^2}{12}\frac{cos3\psi +3cos\psi }{{(a_4^{2}si{n}^2\psi +b_4^{2}co{s}^2\psi )}^{\frac{3}{2}}}\left]-\left(a_3{b}_3^3\right)\right[\frac{1}{b_3}-\frac{1}{3b_3}-\frac{cos\psi }{{(a_3^{2}si{n}^2\psi +b_3^{2}co{s}^2\psi )}^{\frac{1}{2}}}$

$+\frac{b_3^2}{12}\frac{cos3\psi +3cos\psi }{{(a_3^{2}si{n}^2\psi +b_3^{2}co{s}^2\psi )}^{\frac{3}{2}}}\left]+\frac{1}{3}\right[\frac{a_4^3{b}_4^{3}si{n}^2\psi cos\psi }{{(a_4^{2}si{n}^2\psi +b_4^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$-\frac{a_3^3{b}_3^{3}si{n}^2\psi cos\psi }{{(a_3^{2}si{n}^2\psi +b_3^{2}co{s}^2\psi )}^{\frac{3}{2}}}]\}.$   (3)

After infarction, the ellipsoidal segment is bulged out to a different ellipsoidal segment. For the innermost layer, the inner and the outer surfaces of the segments whose major and minor semi-axes are $\left(A1,B1\right)$ and $\left(A2,B2\right)$  subtend the angles $2{\beta }_1$ and $2{\beta }_2$ at their centers. Similarly, for the middle and outer bulged segments having $\left(A2,B2\right),\left(A3,B3\right)$ and $\left(A3,B3\right),\left(A4,B4\right)$ as the semi-axes, angles subtended at the centre are $2{\beta }_2$ and $2{\beta }_3$  and $2{\beta }_3$ and $2{\beta }_4$ respectively.

Now the volumes of different bulged out segments are

$VI\left(inner\right)=\pi \{\left(A_2{B}_2^3\right)[\frac{1}{B_2}-\frac{1}{3B_2}-\frac{cos{\beta }_2}{{(A_2^{2}si{n}^2{\beta }_2+B_2^{2}co{s}^2{\beta }_2)}^{\frac{1}{2}}}$

$+\frac{B_2^2}{12}\frac{cos3{\beta }_2+3cos{\beta }_2}{{(A_2^{2}si{n}^2{\beta }_2+B_2^{2}co{s}^2{\beta }_2)}^{\frac{3}{2}}}\left]-\left(A_1{B}_1^3\right)\right[\frac{1}{B_1}-\frac{1}{3B_1}-\frac{cos{\beta }_1}{{(A_1^{2}si{n}^2{\beta }_1+B_1^{2}co{s}^2{\beta }_1)}^{\frac{1}{2}}}$

$+\frac{B_1^2}{12}\frac{cos3{\beta }_1+3cos{\beta }_1}{{(A_1^{2}si{n}^2{\beta }_1+B_1^{2}co{s}^2{\beta }_1)}^{\frac{3}{2}}}\left]+\frac{1}{3}\right[\frac{a_2^3{b}_2^{3}si{n}^2\psi cos\psi }{{(a_2^{2}si{n}^2\psi +b_2^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$-\frac{a_1^3{b}_1^{3}si{n}^2\psi cos\psi }{{(a_1^{2}si{n}^2\psi +b_1^{2}co{s}^2\psi )}^{\frac{3}{2}}}]\},$   (4)

$VI\left(Middle\right)=\pi \{\left(A_3{B}_3^3\right)[\frac{1}{B_3}-\frac{1}{3B_3}-\frac{cos{\beta }_3}{{(A_3^{2}si{n}^2{\beta }_3+B_3^{2}co{s}^2{\beta }_3)}^{\frac{1}{2}}}$

$+\frac{B_3^2}{12}\frac{cos3{\beta }_3+3cos{\beta }_3}{{(A_3^{2}si{n}^2{\beta }_3+B_3^{2}co{s}^2{\beta }_3)}^{\frac{3}{2}}}\left]-\left(A_2{B}_2^3\right)\right[\frac{1}{B_2}-\frac{1}{3B_2}-\frac{cos{\beta }_2}{{(A_2^{2}si{n}^2{\beta }_2+B_2^{2}co{s}^2{\beta }_2)}^{\frac{1}{2}}}$

$+\frac{B_2^2}{12}\frac{cos3{\beta }_2+3cos{\beta }_2}{{(A_2^{2}si{n}^2{\beta }_2+B_2^{2}co{s}^2{\beta }_2)}^{\frac{3}{2}}}\left]+\frac{1}{3}\right[\frac{a_3^3{b}_3^{3}si{n}^2\psi cos\psi }{{(a_3^{2}si{n}^2\psi +b_3^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$-\frac{a_2^3{b}_2^{3}si{n}^2\psi cos\psi }{{(a_2^{2}si{n}^2\psi +b_2^{2}co{s}^2\psi )}^{\frac{3}{2}}}]\}$   (5)

 and

$VI\left(outer\right)=\pi \{\left(A_4{B}_4^3\right)[\frac{1}{B_4}-\frac{1}{3B_4}-\frac{cos{\beta }_4}{{(A_4^{2}si{n}^2{\beta }_4+B_4^{2}co{s}^2{\beta }_4)}^{\frac{1}{2}}}$

$+\frac{B_4^2}{12}\frac{cos3{\beta }_4+3cos{\beta }_4}{{(A_4^{2}si{n}^2{\beta }_4+B_4^{2}co{s}^2{\beta }_4)}^{\frac{3}{2}}}\left]-\left(A_3{B}_3^3\right)\right[\frac{1}{B_3}-\frac{1}{3B_3}-\frac{cos{\beta }_3}{{(A_3^{2}si{n}^2{\beta }_3+B_3^{2}co{s}^2{\beta }_3)}^{\frac{1}{2}}}$

$+\frac{B_3^2}{12}\frac{cos3{\beta }_3+3cos{\beta }_3}{{(A_3^{2}si{n}^2{\beta }_3+B_3^{2}co{s}^2{\beta }_3)}^{\frac{3}{2}}}\left]+\frac{1}{3}\right[\frac{a_4^3{b}_4^{3}si{n}^2\psi cos\psi }{{(a_4^{2}si{n}^2\psi +b_4^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$-\frac{a_3^3{b}_3^{3}si{n}^2\psi cos\psi }{{(a_3^{2}si{n}^2\psi +b_3^{2}co{s}^2\psi )}^{\frac{3}{2}}}]\}.$   (6)

Using Figure 1 and considering the incompressibility conditions, we get the following geometrical relations:

$A_1=\frac{a_{1}sin\psi }{sin{\beta }_1}{[\frac{\left(1-e^2\right)\left(1-e_1^{2}co{s}^2{\beta }_1\right)}{\left(1-e_1^2\right)\left(1-e^{2}co{s}^2\psi \right)}]}^{\frac{1}{2}},$   (7)

$A_2=\frac{a_{2}sin\psi }{sin{\beta }_2}{[\frac{\left(1-e^2\right)\left(1-e_1^{2}co{s}^2{\beta }_2\right)}{\left(1-e_1^2\right)\left(1-e^{2}co{s}^2\psi \right)}]}^{\frac{1}{2}},$   (8)

$A_3=\frac{a_{3}sin\psi }{sin{\beta }_3}{[\frac{\left(1-e^2\right)\left(1-e_1^{2}co{s}^2{\beta }_3\right)}{\left(1-e_1^2\right)\left(1-e^{2}co{s}^2\psi \right)}]}^{\frac{1}{2}}$   (9)

 and

$A_4=\frac{a_{4}sin\psi }{sin{\beta }_4}{[\frac{\left(1-e^2\right)\left(1-e_1^{2}co{s}^2{\beta }_4\right)}{\left(1-e_1^2\right)\left(1-e^{2}co{s}^2\psi \right)}]}^{\frac{1}{2}}.$   (10)

Making use of the relations (1)-(6) together with (7)-(10), the differences in the volumes before and after the formation of the aneurysm of the inner, middle and outer portions are found as

$V-VI\left(inner\right)=\frac{\pi }{12}\{\frac{2}{3}[\left(1-e^2\right)\left(a_2^3-a_1^3\right)-\frac{{(1-e^2)}^{\frac{3}{2}}si{n}^3\psi }{{(1-e_1^2)}^{\frac{1}{2}}{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$\left(\frac{{(1-e_1^{2}co{s}^2{\beta }_2)}^{\frac{3}{2}}{a}_2^3}{si{n}^3{\beta }_2}-\frac{{(1-e_1^{2}co{s}^2{\beta }_1)}^{\frac{3}{2}}{a}_1^3}{si{n}^3{\beta }_1}\right)]-[\frac{cos\psi {(1-e^2)}^{\frac{3}{2}}}{{(1-e^{2}co{s}^2\psi )}^{\frac{1}{2}}}\left(a_2^3-a_1^3\right)$

$-\left(\frac{1-e^2}{1-e^{2}co{s}^2\psi }{)}^{\frac{3}{2}}si{n}^3\psi \left(\frac{cos{\beta }_2}{si{n}^3{\beta }_2}\left(1-e_1^{2}co{s}^2{\beta }_2\right)a_2^3-\frac{cos{\beta }_1}{si{n}^3{\beta }_1}\left(1-e_1^{2}co{s}^2{\beta }_1\right)a_1^3\right)\right]$

$+\frac{1}{12}[\frac{{(1-e^2)}^{\frac{5}{2}}\left(cos3\psi +3cos\psi \right)\left(a_2^3-a_1^3\right)}{{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}-\frac{\left(1-e_1^2\right){(1-e^2)}^{\frac{3}{2}}}{{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}si{n}^3\psi$

$\left(\frac{cos3{\beta }_2+3cos{\beta }_2}{si{n}^3{\beta }_2}{a}_2^3-\frac{cos3{\beta }_1+3cos{\beta }_1}{si{n}^3{\beta }_1}{a}_1^3\right)]\},$   (11)

$V-VI\left(middle\right)=\pi \{\frac{2}{3}[\left(1-e^2\right)\left(a_3^3-a_2^3\right)-\frac{{(1-e^2)}^{\frac{3}{2}}si{n}^3\psi }{{(1-e_1^2)}^{\frac{1}{2}}{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$\left(\frac{{(1-e_1^{2}co{s}^2{\beta }_3)}^{\frac{3}{2}}{a}_3^3}{si{n}^3{\beta }_3}-\frac{{(1-e_1^{2}co{s}^2{\beta }_2)}^{\frac{3}{2}}{a}_2^3}{si{n}^3{\beta }_2}\right)]-[\frac{cos\psi {(1-e^2)}^{\frac{3}{2}}}{{(1-e^{2}co{s}^2\psi )}^{\frac{1}{2}}}\left(a_3^3-a_2^3\right)$

$-\left(\frac{1-e^2}{1-e^{2}co{s}^2\psi }{)}^{\frac{3}{2}}si{n}^3\psi \left(\frac{cos{\beta }_3}{si{n}^3{\beta }_3}\left(1-e_1^{2}co{s}^2{\beta }_3\right)a_3^3-\frac{cos{\beta }_2}{si{n}^3{\beta }_2}\left(1-e_1^{2}co{s}^2{\beta }_2\right)a_2^3\right)\right]$

$+\frac{1}{12}[\frac{{(1-e^2)}^{\frac{5}{2}}\left(cos3\psi +3cos\psi \right)\left(a_3^3-a_2^3\right)}{{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}-\frac{\left(1-e_1^2\right){(1-e^2)}^{\frac{3}{2}}}{{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}si{n}^3\psi$

$\left(\frac{cos3{\beta }_3+3cos{\beta }_3}{si{n}^3{\beta }_3}{a}_3^3-\frac{cos3{\beta }_2+3cos{\beta }_2}{si{n}^3{\beta }_2}{a}_2^3\right)]\}$   (12)

 and

$V-VI\left(outer\right)=\pi \{\frac{2}{3}[\left(1-e^2\right)\left(a_4^3-a_3^3\right)-\frac{{(1-e^2)}^{\frac{3}{2}}si{n}^3\psi }{{(1-e_1^2)}^{\frac{1}{2}}{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}$

$\left(\frac{{(1-e_1^{2}co{s}^2{\beta }_4)}^{\frac{3}{2}}{a}_4^3}{si{n}^3{\beta }_4}-\frac{{(1-e_1^{2}co{s}^2{\beta }_3)}^{\frac{3}{2}}{a}_3^3}{si{n}^3{\beta }_3}\right)]-[\frac{cos\psi {(1-e^2)}^{\frac{3}{2}}}{{(1-e^{2}co{s}^2\psi )}^{\frac{1}{2}}}\left(a_4^3-a_3^3\right)$

$-\left(\frac{1-e^2}{1-e^{2}co{s}^2\psi }{)}^{\frac{3}{2}}si{n}^3\psi \left(\frac{cos{\beta }_4}{si{n}^3{\beta }_4}\left(1-e_1^{2}co{s}^2{\beta }_4\right)a_4^3-\frac{cos{\beta }_3}{si{n}^3{\beta }_3}\left(1-e_1^{2}co{s}^2{\beta }_3\right)a_3^3\right)\right]$

$+\frac{1}{12}[\frac{{(1-e^2)}^{\frac{5}{2}}\left(cos3\psi +3cos\psi \right)\left(a_4^3-a_3^3\right)}{{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}-\frac{\left(1-e_1^2\right){(1-e^2)}^{\frac{3}{2}}}{{(1-e^{2}co{s}^2\psi )}^{\frac{3}{2}}}si{n}^3\psi$

$\left(\frac{cos3{\beta }_4+3cos{\beta }_4}{si{n}^3{\beta }_4}{a}_4^3-\frac{cos3{\beta }_3+3cos{\beta }_3}{si{n}^3{\beta }_3}{a}_3^3\right)]\}.$   (13)

The expressions (11)-(13) should be equal to zero on account of the incompressibility condition.

Stress equations of equilibrium and length-tension relationship of the muscle layers for the inner and outer bulges of the aneurysm

Let $p$ be the left ventricular pressure of the undamaged portion of the ventricle, $T$ the uniform circumferential stress in all layers of the undamaged ventricle and $T_{{\beta }_2},T_{{\beta }_3}$  the tensile stresses on the inner and outer surfaces of middle segment of the bulged portion. For the equilibrium of the undamaged ventricle, we have

$p{b}_1^2=T\left(b_4^2-b_1^2\right).$   (14)

Considering a segment of the innermost layer of the undamaged left ventricle, we find that it is in equilibrium under the action of the ventricular pressure on its inner surface and a pressure $p_f$ exerted by the liquid phase of the infarcted region. Thus we can write

$p{B}_1^2-p_f{B}_2^2=\left(B_2^2-B_1^2\right)T_{{\beta }_2}.$    (15)

Similarly, if we consider a segment of the outermost layer, we may observe that the pressure $p_f$ is exerted on its inner surface, while the outer surface is free of tractions. Thus in order that the equilibrium of this segment is maintained, we must have

$p_f{B}_3^2=\left(B_4^2-B_3^2\right)T_{{\beta }_3}.$   (16)

Elimination of the quantities $p$ and $p_f$  from the equations (14)-(16) yields

$B_1^2\left(\frac{B_4^2-B_1^2}{B_1^2}\right)T-\frac{B_2^2}{B_3^2}\left(B_4^2-B_3^2\right)T_{{\beta }_3}=\left(B_2^2-B_1^2\right)T_{{\beta }_2}.$   (17)

 This equation may be written in the form

$\frac{B_1}{b_1{B}_1}\left[1-\left(1-\frac{B_3}{B_4}\right)\left(\frac{T_{{\beta }_3}}{T}-1\right)\right]=\frac{B_4}{b_4{B}_3}\left[1+\frac{b_1^2}{b_4^2}\left(\frac{B_2}{B_1}-1\right)\left(\frac{T_{{\beta }_2}}{T}-1\right)\right].$   (18)

In the sequel, we shall make use of the following approximations:

$\begin{array}{l}{B}_3\approx B_4,1+\frac{B_3}{B_4}\approx 2.\\ B_1\approx B_2,1+\frac{B_2}{B_1}\approx 2.\\ and\frac{B_1{B}_3}{B_2{B}_4}\approx \frac{b_1}{b_4}.\end{array}$

These approximations are valid for the case when the innermost and the outermost layers of the infarcted region of the left ventricle under consideration are sufficiently thin.

Now using the geometric relations (7)-(10) , we have from (18):

$\frac{1}{a_2}{(\frac{1-e_1^{2}co{s}^2{\beta }_1}{1-e_1^{2}co{s}^2{\beta }_2})}^{\frac{1}{2}}\frac{sin{\beta }_2}{sin{\beta }_1}\{1-[1-\frac{a_3{(1-e_1^{2}co{s}^2{\beta }_3)}^{\frac{1}{2}}sin{\beta }_4}{a_4{(1-e_1^{2}co{s}^2{\beta }_4)}^{\frac{1}{2}}sin{\beta }_3}]\left(\frac{T_{{\beta }_3}}{T}-1\right)\}$

$=\frac{1}{a3}{(\frac{1-e_1^{2}co{s}^2\beta 4}{1-e_1^{2}co{s}^2{\beta }_2})}^{\frac{1}{2}}\frac{sin{\beta }_3}{sin\beta 4}\{1+\frac{a_1^2}{a_4^2}[\frac{a_2{(1-e_1^{2}co{s}^2{\beta }_2)}^{\frac{1}{2}}sin{\beta }_1}{a_1{(1-e_1^{2}co{s}^2{\beta }_1)}^{\frac{1}{2}}sin{\beta }_2}]\left(\frac{T_{{\beta }_2}}{T}-1\right)\}.$   (19)

The bulge factor defined as the ratio of the height of the bulge above the centre of curvature to the pre-infarct height is given by

$H_{{\beta }_2}=A_2\left(1-cos{\beta }_2\right)/\left[a_2\left(1-cos\psi \right)\right]\left(fortheinnerbulge\right)$   (20)

 and

$H_{{\beta }_3}=A_3\left(1-cos{\beta }_3\right)/\left[a_3\left(1-cos\psi \right)\right]\left(fortheouterbulge\right).$   (21)

The contractile muscle stress ratios $T_{{\beta }_2}/T$  and $T_{{\beta }_3}/T$  are defined as the ratio of the average stresses in the infarcted region to the stresses in the corresponding non-infarcted zone. For cardiac muscle, the contractile tension is a linear function of the contracted length. Thus the tension factor may be expressed as

$\frac{T_{{\beta }_2}}{T}=\frac{A_2{{\displaystyle \int }}_0^{{\beta }_2}\sqrt{1-e_1^{2}co{s}^2{\beta }_2}d{\beta }_2-a_{20}{{\displaystyle \int }}_0^{\psi }\sqrt{1-e^{2}co{s}^2\psi }d\psi }{a_2{{\displaystyle \int }}_0^{\psi }\sqrt{1-e^{2}co{s}^2\psi }d\psi -a_{20}{{\displaystyle \int }}_0^{\psi }\sqrt{1-e^{2}co{s}^2\psi }d\psi }$   (22)

 = ratio of tensile stresses in the strained outer bulged layer to the tensile stresses in the unstrained normal layer,

$\frac{T_{{\beta }_3}}{T}=\frac{A_3{{\displaystyle \int }}_0^{{\beta }_3}\sqrt{1-e_1^{2}co{s}^2{\beta }_3}d{\beta }_3-a_{30}{{\displaystyle \int }}_0^{\psi }\sqrt{1-e^{2}co{s}^2\psi }d\psi }{a_3{{\displaystyle \int }}_0^{\psi }\sqrt{1-e^{2}co{s}^2\psi }d\psi -a_{30}{{\displaystyle \int }}_0^{\psi }\sqrt{1-e^{2}co{s}^2\psi }d\psi }$   (23)

 =ratio of tensile stresses in the strained inner bulged layer to the tensile stresses in the unstrained normal layer.

In the above expressions, $a_{20}$ and $a_{30}$ represent the semi major axes of the inner and outer bulged layers in the state of zero stresses; their values are nearly 0.75 of their corresponding values in the deformed state.

Numerical results

The expressions (11)-(13) when equated to zero(due to incompressibility condition) yield three equations involving the parameters ${\beta }_1,\beta 2,\beta 3$ and ${\beta }_4$ . The same parameters are also involved in the equation (19). This set of four equations was solved by employing the Newton-Raphson method. The values of ${\beta }_1,\beta 2,\beta 3 and {\beta }_4$ thus obtained were used while computing the values of the tension factors as well as the bulge heights. For computational work, the cavity volume was taken to be 135 ml; also the following values of the parameters were used:

$\begin{array}{l}e=0.4931,e_1=0.435,a_1=3.4874\\ a_2=3.5971,a_3=4.5847,and{a}_4=\mathrm{4.6944.}\end{array}$

Four values of ψ (half the angle of damage) viz. ${10}^o,{20}^o,{30}^{o}and{40}^o$ were examined.

Numerical results of the computational work carried out on the basis of the present analytical study are shown in Table 1.

The order of magnitude of the above values agrees with the corresponding values of Radhakrishnan et al.²⁹ who considered a spherical shell model for the left ventricular geometry by taking help of different approximations. For the sake of a comparison of the results of the present study with the those of,²⁹ the results corresponding to $2\psi ={40}^{o}and{60}^o$ are shown in Table 2.

The line $T_{{\beta }_2}=5$  is found to intersect the plot for $T_{{\beta }_2}$ of our present study (Figure 2) at a point whose abscissa is ${47}^o$ while this value was found to be ${35}^o$ by Radhakrishnan et al.²⁹ This difference may be attributed to the combined effect of eccentricity and layered structure of the left ventricle, considered in our study.

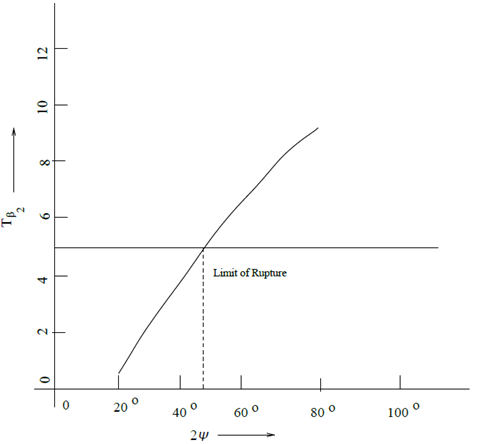
Figure 2 Tension factor for the inner bulge vs. angle of damage.

On the basis of a previous analytical study, Misra et al.³⁰ made an important conjecture that a larger amount of blood is likely to be ejected, whenever there is an increase in the diastolic filling, owing to a forceful contraction of the left ventricle of the heart. The present study is aimed at an analytical investigation of the effects of structural geometry of the left ventricle in a specific pathological state. The non-homogeneity of the ventricular tissues has also been incorporated in the mathematical analysis. Since observed data from experiments with sub-human primates cannot be readily applied to humans, theoretical models studied by means of mathematical analyses play very important roles in exploring a variety of information on the anatomy and physiology of human bodies. This is why the present study is of immense help in the studies pertaining to the infarcted state of the human left ventricle. The present study is particularly useful to validate the results of relevant experimental investigations with animals e.g. rhesus monkeys, and also those of finite element studies on left ventricular aneurysms. Regarding the scope for further studies, it is suggested that the analytical expressions presented here may be computed numerically in a more exhaustive manner, so as to derive further information on the pathological state of the left ventricle by using more advanced computational techniques. One can also use softwares like mathematica to derive numerical results for the variation of a number of parameters involved in the present study.

A theoretical study on the effect of structure and mechanics on ventricular aneurysms has been presented in the paper. For this purpose, a mathematical model has been developed, by considering the layered structure of the left ventricle and treating it as an ellipsoidal shell The merit of the model is that unlike most other models considered by previous investigators, our model enables us to take into account the heterogeneous structure and the eccentricity of the left ventricle. Based on the study, it may be concluded that both the layered structure of the left ventricular aneurysm and its geometrical configuration have important bearings on formation of the aneurysm structure.

The authors wish to express their deep sense of gratitude to the reviewers for their kind words of appreciation of the scientific content of the work and also for their esteemed comments based on which the revised manuscript has been prepared.

None.

None.

1. Bartel T, Vanheiden H, Schaar J, et al. Biomechanical Modeling of Hemodynamic Factors Determining Bulging of Ventricular Aneurysms. Ann of Thorac Surg. 2002;74(5):1581–1587.
2. Huxley AF. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318.
3. Hill AV. Muscular Activity. Williams and Wilkins, Battimore. 1956.
4. Van Den Broek JHJM, Van Den Broek MHLM. Application of an ellipsoidal heart model in studying left ventricular contractions. J Biomech. 1980;13(6):493–503.
5. Moskowitz SE. On the mechanics of left ventricular diastole. Journal of Biomechanics. 1980;13(3):301–311.
6. Misra JC, Singh SI. Distribution of the stress in the left ventricular wall of impact heart. Bulletin of Mathematical Biology. 1985;47(1):53–71.
7. Misra JC, Singh SI. A Model for Studying the Stability of Thoracic aorta. Mathematical Modelling. 1985;6(4):295–306.
8. Misra JC, Singh SI. Pulse wave velocities in the aorta. Bulletin of Mathematical Biology. 1984;46(1):103–114.
9. Misra JC, Singh SI. A large deformation analysis for aortic wall under a physiological loading. International Journal of Engineering Science. 1983;21(10):1193–1202.
10. Misra JC, Singh SI. Study on the mechanics of aneurysms in the left ventricle of the heart. Computers and Mathematics with Applications. 1988;15(1):17–27.
11. Taber LA, Podszus WW. A laminated shell model for the infarcted left ventricle. International Journal of Solids and Structures. 1997;34(2):223–241.
12. Holmes JW, Borg TK, Covell JW. Structure and mechanics of healing myocardial infarcts. Annual Review of Biomedical Engineering. 2005;7:223–253.
13. Cheng TO. History of coronary artery bypass surgery - half of a century of progress. International Journal of Cardiology. 2012;157(1):1–2.
14. Ren J, Yuan X. Mechanics of formation and rupture of human aneurysm. Applied Mathematics and Mechanics. 2010;31:593–604.
15. Misra JC, Sinha A, Shit GC. Flow of a Biomagnetic Viscoelastic Fluid: Application to Estimation of Blood Flow in arteries during Electromagnetic Hyperthermia, a Therapeutic Procedure for Cancer Treatment. Applied Mathematics and Mechanics. 2010;31(11):1405–1420.
16. Mallick B, Misra JC, Chowdhury AR. Influence of Hall current and Joule heating on entropy generation during electrokinetically induced thermoradiative transport of nanofluids in a porous microchannel. Applied Mathematics and Mechanics. 2019;40(10):1509–1530.
17. Misra JC, Chandra S, Shit GC, et al. Electroosmotic Oscillatory Flow of Micropolar Fluid in Microchannels: Application to dynamics of blood flow in Microfluidic Devices. Applied Mathematics and Mechanics. 2014;35(6):749–766.
18. Sui Y, Teng S, Qian J, et al. Treatment outcomes and therapeutic evaluations of patients with left ventricular aneurysms. Journal of International Medical Research. 2019;47(1):244–251.
19. Ohlow MA. Congenital left ventricular aneurysms and diverticula: an entity in search of an identity. Journal of Geriatric Cardiology. 2017;14(12):750–762.
20. Coskun KO, Popov AF, Coskun ST, et al. Surgical treatment of left ventricular aneurysm. Asian Cardiovascular and Thoracic Annals. 2009;17(5):490–493.
21. Mujanovic E, Bergslan J, Avdic S, et al. Surgical treatment of left ventricular pseudoaneurysm. Medical Archives. 2014;68(3):215–217.
22. Mukaddirov M, Demaria RG, Perrault LP, et al. Reconstructive surgery of postinfarction left ventricular aneurysms: techniques and unsolved problems. European Journal of Cardio-Thoracic Surgery. 2008;34(2):256–261.
23. Yan J, Jiang SL. Impact of surgical ventricular restoration on early and long-term outcomes of patients with left ventricular aneurysms. Medicine. 2018;97(41):e12773.
24. Antunes PE, Silva R, Oliveira JF, et al. Left ventricular aneurysms: early and long-term results of two types of repair. European Journal of Cardio-Thoracic Surgery. 2005;27(2):210–215.
25. Wang X, He X, Mei Y, et al. Early results after surgical treatment of left Ventricular Aneurysm. Journal of Cardiothoracic Surgery. 2012;7:126.
26. Pasque MK. Mathematic modeling and cariac sugery. The Journal of Thoracic and Cardiovascular Surgery. 2002;123(4):617–620.
27. Kramer CM, Magovern JA, Rogers WJ, et al. Reverse remodeling and improved regional function after repair of left ventricular aneurysm. The Journal of Thoracic and Cardiovascular Surgery. 2002;123(4):700–706.
28. Guccionne JM, Moonly SM, Moustakidis P, et al. Mechanism underlying mechanical dysfunction in the border zone of of left ventricular aneurysm: a finite element study. The Annals of Thoracic Surgery. 2001;71(2):654–662.
29. Radhakrishnan S, Ghista DN, Jayaraman G. Mechanical analysis of the development of left ventricular aneurysms. Journal of Biomechanics. 1980;13(12):1031–1039.
30. Misra JC, Dandapat S, Adhikary SD. Stress distribution in the left ventricular wall during cardiac contraction: study of a mathematical model. J Mechs Medicine and Biology. 2021;21:2150015.