The paper presents a center of mass as an imaginational point which helps in analysis of different human body configurations, both in static and movement conditions. To maintain a balance one need in static condition to keep projection of center of mass above an area of equilibrium while during a movement a resultant force of gravity and centrifugal force need to go through the area of equilibrium. Center of mass helps in drawing an angle of equilibrium. During a movement one can use center of mass as a point which substitutes the whole body in description of sinusoidal locomotion of the human body in vertical and horizontal planes. Main direct and indirect methods of localization of human body center of mass were given. Also applications of knowledge on location of center of mass were presented.

Keywords: human body, center of mass, balance, statics, movement

During the process of biomechanical analysis in order to present a body one can use specific point localized on the body, e.g. central geometric point or some point at the edge of the body. Taking into account human body this specific point can be e.g. a top of head, an ear, or a hip joint. Such a point plays a role during simplification of the body. If one wants to describe trajectory of body’s movement he or she can use a specific point which would substitute the whole body. The best representation of the body is its center of mass. This is an imaginational point not joined with material representation of the body. It can move outside the body like in an example of a circle. Since the human body has complicated shape and is built from many tissues of different density it is not easy to localize position of human body center of mass. Usually it is localized with the use of radius of center of mass, i.e. a distance from the center of mass to the reference system. Center of mass plays also a role of a point of application of forces – gravitational force and inertial force, including centrifugal force.^1,2

There are several methods of localization of the center of mass, both direct and indirect. There are also many applications of the knowledge on location of the center of mass of the body in maintaining balance, in analyses of locostationary and locomotory behavior within the areas of everyday living, medicine, engineering, ergonomics, sport.³ The aim of the paper is to present center of mass as imaginational point which helps in biomechanical description of different configurations of the human body during maintaining static posture and during locostationary and locomotory movements.

Main direct approaches with live subjects

The oldest approach to localization of center of mass was performed by Borelli⁴ in the 17th century. He put a board on a prism in such a manner that a board was in equilibrium. Then a man was laid on a board. He moved toward the head or toward the feet to maintain equilibrium of the whole system – board and the body. In the 19th century Du Bois-Reymond put two short edges of a board (reaction board) on two prisms. One prism was rested on a scale. The value of partial weight of a board resting on a scale was read out. With known body weight, measured distance between prisms, and reading of scale value, one could calculate position of body’s center of mass remembering of subtracting partial weight of a board. Also in the 19th century Basler developed this method by using three-sided board. He obtained position of center of mass in two directions. All above approaches were direct investigations on location of the whole body center of mass. They were used for one configuration of the body.⁵

Main direct approaches with cadavers

In order to obtain position of center of mass in different configurations Harless,⁶ Braune & Fischer⁷ in the 19th century, and then especially Dempster & Clauser et al.^8,9 in the 20th century divided frozen cadavers onto separate body parts. They measured mass and volume and calculated density, and also they positioned center of mass of each body part. From them only Dempster divided the trunk onto four parts: thorax, abdomino-pelvic region, two shoulders. Others kept the trunk as a one segment. In addition to inertial values (mass and radius of center of mass) Clauser et al.⁹ measured dimensions of body parts and skin-fat thickness above iliac crest. They proposed equations where dependent variable was body part mass or radius of center of mass and independent variables were whole body mass and dimensions of body parts.

Main indirect approaches with live subjects

Zatsiorsky & Seluyanov¹⁰ used gamma scanning for obtaining inertial data. They obtained mass, radius of mass and moment of inertia of 100 live subjects. They were mostly students of physical education major. Zatsiorsky and Seluyanov divided the trunk into three parts with planes perpendicular to the longitudinal axis. Erdmann and Gos obtained densities of 50 trunk tissues.¹¹ Then, Erdmann used computerized tomography in order to obtain geometric and inertial data of the male trunk.^1,2 On the picture of trunk layers he differentiated tissues belonging to separate trunk parts: pelvis, abdomen, thorax, two shoulders. Having volumes of tissues Erdmann presented equations for obtaining volume of unchangeable tissues together (bones, lungs, liver, circulation tissues, visceral tissues) of a new subject. Changeable tissues (skin and fat) has to be obtained by direct measurement of skin-fat folds in few places and then regression equations are used for obtaining volume of fat tissues and of the skin for separate trunk parts. Then muscle tissue is obtained by subtracting from the whole volume of body parts volume of unchangeable tissues and skin and fat tissue. During the investigation a subject is photographed from two sides or a laser scanner is used in order to obtain volume of trunk layers and then trunk parts. Inertial data of extremities are still obtained using a Clauser et al.⁹ approach. When comparing above indirect method with direct (Du Bois Reymond) method the outcome was almost identical. For the whole body mass Pearson coefficient r=0.998, for the radius of center of mass from the soles r=0.995.¹² Other researchers used for obtaining inertial segment parameters nuclear magnetic resonance imaging, e.g. Martin et al.¹³ and dual energy X-ray absorptiometry (DEXA) imaging, e.g. Durkin & Dowling.¹⁴

Mass of body parts and location of its centers of mass

Based on data gathered by several authors relative mass (in %) of body parts for untrained adult males (but not overweight) is as follows: head 5, neck 3, thorax 11, abdomen 16, pelvis 11, shoulder 5, arm 3, forearm 2, hand 1, thigh 10, shank 4, foot 2. Trained males and those with longer lower extremities have usually higher data of mass of thigh (11) and shank (5) and less mass of shoulder 4, abdomen 14. According to Erdmann’s data^1,2 when the length of a trunk, i.e. distance between base of a neck (cervicale) and a line connecting hip joints, could be presented as 100%, so location of centers of mass of trunk parts is as follows: pelvis 7% from the hips, abdomen 40% from the hip, thorax 28% from the base of a neck. A mass of a shoulder is obtained as follows: a) a level at a distance of 35 % from a base of a neck is obtained; b) in sagittal plane an auxiliary point is drawn 35 % from the back where 100% is an antero-posterior distance; in frontal plane at the same 35% distance from a base of a neck a line is drawn to the side of a trunk, then along this half-trunk distance an auxiliary point is drawn 41% from the trunk’s center; c) from the auxiliary point a line is drawn to the arm axis and then on this line center of mass of a shoulder is drawn 49% from arm axis. For parts of extremities a length of a part is acquired as 100%. According to Clauser et al.⁹ location of center of mass for thigh, shank, forearm is 43% from the proximal end, for an arm and foot there is 44%. For a hand there is 37% from the wrist when extended and 51% when flexed in proximal interphalangeal joints.

Finding common centers of mass

When masses and location of centers of mass of body parts are obtained one can use one of two methods in obtaining location of center of mass of the whole body. The first one is sum of masses (graphical) method, the other is sum of moments of masses (analytical) method. For the first method data on two adding masses and distance between them should be taken into account. For example common center of mass of foot and shank can be obtained by connecting centers of mass of foot and shank. The common center of mass will lie on a line connecting these two centers of mass. Comparison of values of adding masses gives information on location of common center of mass from the center of mass of a shank. Here, mass of a lighter part is divided by sum of added masses and then multiplied by the distance between two masses. Using this approach one can obtain further common centers of mass up to the center of mass of the whole body. For the second method a reference system is used drawn near the centers of mass of two body parts. Then distances are measured between centers of mass and the reference system (for both axes). Next, masses are multiplied by distances separately for both axes. Thus moments of mass are obtained. These moments are summed and the result is divided by sum of masses. This gives a distance of common center of body parts from the reference system. For the whole body center of mass one need to make projection onto the reference system of all centers of mass of body parts. The sum of moments of masses method is used for computerized approach where instead of centers of mass a position of joints is given for computer program. Next, all necessary calculations are performed by a computer program.

Static positions

Taking into account mechanical explanation of conservation of balance, a body with greater mass which has larger base and has lower position of center of mass can better maintain balance when is pulled or pushed. As an example there is a position of a coach helping a novice gymnast in executing an exercise. A coach acquires a position with feet far apart and much lowering his or her body. In order to draw an equilibrium angle lines are drawn from the center of mass to the edges of feet. A very good balance maintains also very young baby during a squat position (Figure 1). This gives high value of equilibrium angle (yellow). Trunk is maintained in vertical position. Taking into account feet touching the ground one can draw a line around two feet. The area between the feet including area below the feet is called area of equilibrium. A toddler moves touching all four extremities to the ground, usually hands and knees. In this situation its equilibrium status is very good. In static condition when projection of center of mass moves outside area of equilibrium a person falls down. Some people sitting on a chair make balancing movements forward and backward. This is dangerous situation. Projection of center of mass is near the edge of area of equilibrium. Here the situation happens when projection of center of mass can go outside this area and a person falls down to the rear. Often a head and neck is injured (Figure 2).

Locostationary movement

In judo fighting competitors during an attack have their centers of mass in different locations. An attacker (tori) should have his center of mass lower comparing to location of center of mass of the defender (uke). This is because tori should get below uke’s body and from that position to lift his own body and uke’s body in order to execute a throw. Centers of mass help to draw: a) angle of equilibrium, and b) angle of attack (Figure 3). In a sport of weightlifting common center of mass of a competitor and of a barrel is high above the ground. A barrel can be twice as much of mass comparing to sportsperson’s mass. In order to maintain balance a sportsperson during lifting a barrel moves his or her lower extremities forward and backward. Calculation of vertical mechanical work (weight multiplied by vertical displacement) takes into account separately displacement of center of mass of a sportsperson and of a barrel. Then these two works are added giving the total work done by the weightlifter.¹

Locomotion

During walking a vertical projection on the ground of body center of mass is presented often together with center of pressure (COP). These two points draw during straight walking a sinusoidal line (in mediolateral direction) with higher amplitude of COP. During walking or running COP jumps from one foot to another, while center of mass keeps a space between two feet. If a person would accidentally stop he or she would fall down. Sinusoidal track of center of mass is present also in vertical dimension. It is usually fewcm.¹⁶ But when disabled person is taken into account where he or she suffered disability in lower extremities and walks very slowly, even about 0.5m/s (during normal walking velocity of about 1.5 m/s is achieved) vertical oscillation of center of mass is very small, about 1-2cm and mediolateral oscillation is about 6cm.¹⁷ When dash running is taken into account vertical oscillation of center of mass for sprint running is about 10cm and for long distance running just few cm. For hurdle running center of mass is raised about 40cm above the obstacle. When lower raising of center of mass exists then less energy is needed for clearing the obstacle. Similarly is in high jump and especially in pole vault. When a body is substantially curved over the bar and upper extremities are over the head then while a body clears over the bar a center of mass can go near or a little bit below the bar. But here a body needs to go very close to the bar. Some people say that during a high jump when a body is well curved center of mass goes deep below the bar. But Kowalczyk¹⁸ in his dissertation proved this is untrue. Among 30 high jumpers of international level investigated only once center of mass went a little bit below the bar because a jumper hit the bar. It did not fell down and a jump was accepted. In specific situations like narrow mountain track, or in the case of disease of osteo-muscular or nervous system, using additional equipment like sticks or crutches is very helpful. For analysis of those kinds of locomotion center of mass is used for drawing of angles of equilibrium and for comparison of them without and with using special equipment (Figure 4). During the movement along the curve projection of center of mass can go beyond area of equilibrium. This happens during sprint running, bicycle riding, alpine skiing when competitor makes a turn. In this situation centrifugal force can be of high amount and a runner or rider can lean his or her body to the side. Resultant force of gravity force and centrifugal force should be directed to the place where the body or equipment touches the ground.

Center of mass of the human body or its parts is also used in engineering design of transport vehicles: a) of land vehicles–for driver and passengers, b) boats, especially sailing boats, where counter-ballast of the crew is important factor for maintaining balance, c) airplanes, where especially for gliders or small airplanes with one or two pilots problem of equilibrium is important. After a design is proposed then there are several investigations on safety problems. Displacement of center of mass is taken into account to track the movement of crucial body parts (Figure 5).

Figure 1 Correct position for maintaining balance of a coach (A) and of a small baby which was not taught to assume this position (B): feet far apart (orange arrow), low position of center of mass by flexion of hip and knee joints.

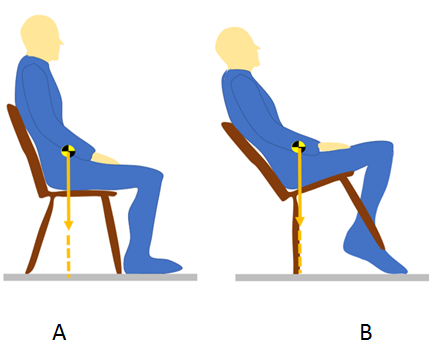
Figure 2 Some people sitting on a chair (A) make balance movements forward and backward (B). When not well controlled an accident happens. It is not recommended to perform such movements.

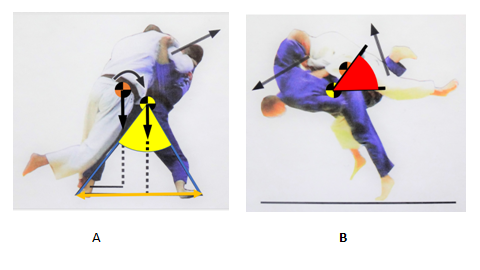
Figure 3In judo attacking competitor during the preparatory move (A) should maintain balance position with feet far apart (orange arrow) obtaining substantial equilibrium angle (yellow) and just before the throw should lower his body and get below opponent’s body (B) obtaining substantial attacking angle (red); black vertical vectors – gravity force, black oblique vectors – activity of muscle force.¹⁵

Figure 4 Increase of angle of equilibrium (about threefold) by using sticks (A) or crutches (B) with its ends far apart (orange arrow).

Figure 5 Model of the human head and neck during car crash tests. Figure based on photograph presented by Hodgson .¹⁹

Analysis of the human body is difficult since it is of irregular shape and is constantly changing its configuration. One of the solutions to this problem can be center of mass. Center of mass is one of the main problems of biomechanics and locomotion. It helps during modelling of the human body and its activity. This point helps in assessment of the technique of static positions and different kinds of movement. It also helps in calculation of work done during lifting. There are several approaches to localization of center of mass. In some situations one can use laboratory approach with the reaction board on which a subject can lie and direct localization of the body center of mass can be obtained. But this needs time and wearing off subject’s clothes. Also this is only for one, regular configuration of the body. For other configurations, especially during movement, one can use different methods. The most convenient method for different tasks and not disturbing a subject (who can be a sportsperson performing movement at the stadium) is taking an image of a subject and then localization of center of mass using one of the indirect methods. Location of center of mass depends on body build and body proportions. Within sportspeople those who train football (soccer), cycling, horizontal jumping have more muscles at lower extremities. They have relative location of center of mass lower. Sportspeople who train gymnastics, fighting sports, athletic throwing has more developed upper body part. They have relatively higher location of center of mass. Women because of more developed lower girdle have center of mass located relatively lower. Zhao et al²⁰ reported research results of previous works^21,22 on differences of lower extremities’ length among ethnic groups with African-American having longer legs than Caucasians and Asians having shorter legs than Caucasians. In young people lower extremities have more muscles than adipose tissue, so location of center of mass of young black people is lower comparing with representatives of other ethnic groups.

Virmavirta & Isolehto²³ compared localization of center of mass using three different approaches: 1) direct method with reaction board, 2) using Dempster’s data, 3) Zatsiorsky and Seluyanov’s data adjusted by de Leva.²⁴ De Leva calculated locations of body parts’ centers of mass from according to anthropological landmarks to according to joints’ axes. Virmavirta and Isolehto observed significant differences in location of center of mass within 1 %. Dempster’s data overestimated data from reaction board, while Zatsiorsky and Seluyanov’s data underestimated data of reaction board. The reason of above discrepancies was Virmavirta and Isolehto used generalized data of Dempster and Zatsiorsky and Seluyanov instead of individual data approach as proposed by Clauser,⁹ Erdmann,² Erdmann & Kowalczyk.¹² Localization of center of mass while standing with asymmetrical load attached to the body is not a difficult task. Wu & McLeod²⁵ investigated subjects who moved whole body center of mass from the center between two feet only half of the distance predicted theoretically. This was investigated for different positions of feet (narrow, medium, wide) and for different loads (10 and 30% of body mass). But intuitive localization of center of mass of objects with irregular, asymmetrical shape shown on the screen is not an easy task. Baud-Bovy & Soechting²⁶ presented results of investigations of subjects who were asked to point center of mass of different two-dimensional objects of different shapes shown on a screen. They concluded that participants tended to locate the center of mass at the center of inscribed circle inside an object instead of the true center of mass.

Unfortunately, localization of center of mass is not easy. It can be computerized but still often needs input on human joints, some end parts like head or hands, and trunk specific points. There are inertial measurement units (IMU) mounted on human body that can give data on positions of joints automatically. These units are costly and they must be mounted on subject’s body. So, the best option is using images of the human body. Taking into account experience of the author in teaching localization of center of mass on a photograph of the body it is difficult task for about a half of university students of physical education major. This should be taught with simple explanations, with several figures, examples, etc. In this way for example a textbook on biomechanics for students of biomedical engineering was published.³

None.

The authors declare, that there is no conflict of interest.

1. Erdmann WS. Geometric and inertial quantities of the male trunk obtained by computerized tomography method (in Polish with English abstract). Gdansk: J Sniadecki University of Physical Education and Sport; 1995.
2. Erdmann WS. Geometric and inertial data of the trunk in adult males. J Biomech. 1997;30(7):679–688.
3. Erdmann WS. Biomechanics: Bases for biomedical engineering major. Poland: Gdansk Technical University; 2015.
4. Borelli JA. De Motu Animalium. Pars prima; Pars Secunda. Lugduni Batavorum (Leiden, Netherlands); 1681.
5. Hochmuth G. Biomechanics of sport movements (in German). Berlin: Sportverlag; 1971.
6. Harless E. Static moments of mass of the human body parts (in German). Abhandlungen der matematisch-physikalischen Klasse der koninglisch-bayerischen Akademie der Wissenschaften. Munich. 1857;8:71–97.
7. Braune W, Fischer O. On center of gravity of the human body with rear view of the equipment of German infantrymen (in German). Abhandlungen der matematisch-physischen Klasse der koniglisch-sachsichen Gesselschaft der Wissenschaften. Leipzig. 1889;15:561–672.
8. Dempster WT. Space requirements of the seated operator. Geometrical, kinematic, and mechanical aspects of the body with special reference to the limbs. Technical Report WADC-TR-55-159. Wright Air Development Center, Air Research and Development Command. United States Air Force and Wright-Patterson Air Force Base. 1955.
9. Clauser CE, McConville JT, Young JW. Weight, volume, and center of mass of segments of the human body. Technical Report AMRL-TR-69-70, Aerospace Medical Research Laboratory, Aerospace Medical Division, Air Force Systems Command and Wright-Patterson Air Force Base. 1969.
10. Zatsiorsky VM, Seluyanov VN. Mass-inertial characteristics of human body segments and their relations with anthropometric landmarks. Voprosy Antropologii. 1979;62:91–103.
11. Erdmann WS, Gos T. Density of trunk tissues of young and medium age people. J Biomech. 1990;23(9):945–947.
12. Erdmann WS, Kowalczyk R. A personalized method for estimating centre of mass location of the whole body based on differentiation of tissues of a multi-divided trunk. J Biomech. 2015;48(1):65–72.
13. Martin PE, Mungiole M, Marzke MW, et al. The use of magnetic resonance imaging for measuring segment inertial properties. J Biomech. 1989;22(4):371–376.
14. Durkin JL, Dowling JJ. Analysis of body segment parameter differences between four human populations and the estimation error of four popular mathematical models. J Biomech Eng. 2003;125(4):515–522.
15. Erdmann WS, Zieniawa R. Biomechanics of judo (in Polish with English abstract). Gdansk: J Sniadecki University of Physical Education and Sport; 2011.
16. Orendurff MS, Segal AD, Klute GK, et al. The effect of walking speed on center of mass displacement. J Rehab Res & Dev. 2004;41(6A):829–834.
17. Gutierrez EM, Bartonek A, Haglund-Akerlind Y, et al. Centre of mass motion during gait in persons with myelomeningocele. Gait Posture. 2002;18(2):37–46.
18. Kowalczyk R. Localization of the center of mass of high jumpers and positioning of the body according to the bar. Doctoral Dissertation, Faculty of Phys. Ed., Gdansk: J. Sniadecki University of Physical Education and Sport; 2013.
19. Hodgson VR. Head model for impact tolerance. In: King WF, Mertz HJ editors. Human impact response. Measurements and simulation. Proceedings of the Symposium on Human Impact Response held at the General Motors Research Laboratories. London: Plenum Press; 1973. p. 113–126.
20. Zhao X, Wang Z, Zhang J, et al. Estimation of total body skeletal muscle mass in Chinese adults: prediction model by dual-energy X-ray absorptiometry. Plos one. 2013;8(1).
21. Eveleth PB, Tanner JM. Worldwide variation in human growth. Cambridge: Cambridge University Press; 1976.
22. Eveleth PB, Tanner JM. Worldwide variation in human growth. 2nd ed. Cambridge: Cambridge University Press; 1990.
23. Virmavirta M, Isolehto J. Determining the location of the body’s center of mass for different groups of physically active people. J Biomech. 2014;47(8):1909–1913.
24. De Leva. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J Biomech. 1996;29(9):1223–1230.
25. Wu G, MacLeod M. The control of body orientation and center of mass location under asymmetrical loading. Gait Posture. 2001;13(2):95–101.
26. Baud-Bovy G, Soechting J. Visual localization of the center of mass of compact, asymmetric, two-dimensional shapes. J Exp Psych Hum Percep Perform. 2001;27(3):692–706.