An automatic method for determining the location of the pulse onset on arterial pulse waves is presented. The aim is to develop an automatic method for enhance the accuracy and precision of pulse onset detection without ECG assistance (R peaks as reference). The approach is composed by two stages: pulse delineator and onset decision. Pulse delineator is based on amplitude and time thresholds computation in time and frequency domain respectively, for locating each pulse wave. Decision stage is based on triangle area algorithm that computes on each pulse the triangle area successive with two fix points and one mobile. The mobile point that corresponds to higher area is the pulse onset. Pulse delineator stage of proposed method was evaluated with CSL database, and their results were comparable to other pulse detection algorithm. Simultaneous ECG and PPG records were used to evaluate the repeatability of proposed method for several signal-noise ratios, as well as the concordance respect to trained observers. The performance of proposed method was compared with ECG assisted methods, such as tangents intersection, diastolic point and second derivative. The approach obtained acceptable values of sensitivity (> 97.99 %), positive predictivity (> 97.91 %), failed rate detection (< 4.11 %) and error (< 5.78 ± 6.64 ms). This proposal found the repeatability condition for each signal-noise ratios. This method could be used on medical systems that need the pulse onset to compute diagnostic markers.

Keywords: arterial pulse, foot point, PPG, pulse delineator, pulse onset, triangle area

Photoplethysmography (PPG) technique is a simple and low-cost optical method used for measuring blood volume changes through of the emission and reception of light on the skin surface of the peripheral body sites such as fingers, ears, toes and forehead.^1–3 PPG has been used in a wide range of investigations and commercial medical equipment for measurement of oxygen saturation, blood pressure trends, heart rate variability, assessing autonomic function, estimate vascular age, age-related changes in pulse rise time, and also detecting peripheral vascular disease.^4–8

The pulses onset detection on PPG signals is used to obtain relevant diagnostic markers such as pulse transit time (PTT) and pulse wave velocity (PWV), to evaluate the vascular effects of aging, hypertension, stiffness and atherosclerosis.^9–12 Several works have demonstrated that PTT and PWV accuracy are affected for automatic method used to compute the characteristic points (onset and middle), due to motion artefacts and noise.^13,14

PPG signal is formed by incident and reflected waveforms, and is affected by natural conditions, location of the sensor, skin characteristics (humidity, color, thickness), respiration, baseline drift, perfusion phenomena, visco-elastic and viscosity property of arteries, arterial stiffness and reflected waves from peripheral sites that modify and amplify the waveform.^13,15,16 Pulse onset detection is a non-trivial task, because pulse onset and early wave can be easily blurred by noise and artefacts due to their intrinsically small amplitude.¹⁷

Onset detection methods have been published with different levels of complexity, including adaptive threshold, computer-based filtering, feature extraction, derivative and stationary wavelet transform calculation.^18–21 Most of these methods are assisted by the electrocardiographic (ECG) signal, which increases the cost of medical equipment and makes difficult their clinical applications in the Health Primary System.^18,19

Shin et al.²² proposed an adaptive threshold method based on virtual reference threshold that follows the morphology of PPG signal. This method shows robustness to breathing interference. Although, its accuracy can be affected by the reflected wave, due to possible high amplitude and short time interval from incident wave provide by age, hypertension and atherosclerosis. Chen et al.²⁰ proposed pre-processing and filtering steps to reduce noise, eliminate peaks and estimate the baseline on the PPG signal. This method uses the baseline for automatic detection of pulse onset to heart rate. This approach has not been statistically validated respect to exactitude and accuracy, but graphic results show that can be a good method for automatic onset detection. Xu et al.¹⁹ makes use of the morphological similarity of adjacent pulse to enhance signal quality and increase the accuracy of the pulses onset detection. They used the time interval between the R peak of ECG and the peak corresponding to three neighbor pulses, for applying the principal components analysis. This idea cannot be satisfied for boundary beats and for beats with missed adjacent R peak detection. This method combined with others algorithms for pulse onset detection such as diastolic point, second derivative and tangent intersection, shows an enhanced accuracy and precision.^18,23,24 Li et al.²⁵ proposed a method to pulse onset, systolic peak and dicrotic notch detection on the arterial blood pressure (ABP) waveforms. This approach is based on zero-crossing point of the first derivative of ABP signal, combined with amplitude and time adaptive threshold makes a final decision about the correct position points. This method presents suitable values of sensitivity, positive predictivity and error rate for onset and systolic peak detection. However, it can be affected by noise and artefacts present in the ABP signal.

Nowadays, most of automatic methods used for pulses onset detection without R peaks as reference are affected by reflected waves, fluctuations and noise of the baseline, motion artefacts, high amplitudes variations due to respiration and others physiologic process, and others. Furthermore, the gold standard for onset definition does not exist.¹⁹

This work presents a new proposal for automatic pulse onset detection on PPG signal, avoiding the use of R peaks as reference. This method is based on short time windows analysis over PPG signal with temporal and spectral techniques to improve the accuracy of pulse detection, and triangle areas algorithm to locate the pulse onset. The approach is validated using CSL database and simultaneous ECG and PPG records acquired on volunteer healthy subjects in the supine and stand-up position, evaluating the any parameters as repeatability coefficient, error, sensitivity, positive predictivity and failed rate for various signal-to-noise ratios.

Figure 1 shows a block diagram which illustrates the proposed method. First, the photoplethysmographic (PPG) signal is filtered with low-pass filter (Butterworth, 2^nd order, cut-off frequency: 16Hz, zero phase) for noise reduction. This signal has a bandwidth from 0.01Hz to 16Hz. Then, filtered signal is processed by a pulse delineator block to find the localization of each pulse. Finally, detected pulses are provided to the decision block to obtain the onsets.

Figure 1 Block diagram for automatic detection of onset pulse.

Pulse delineator block

Pulse delineator block is based on time and amplitude adaptive thresholds, and allows the incident waves localization of each pulse and their discrimination respect to possible spurious and reflected waves. Reflected waves can be modified and amplified by arterial stiffness and others vascular diseases, which causes a fast propagation of arterial pulse wave.²⁶ Hence, the automatic methods can mislead the selection of the incident wave, because the time interval between incident and reflected waves is reduced and their amplitudes values can be comparable.

The pulsatile component of PPG waveform is often called “AC” components and usually has its fundamental frequency, typically around 1 Hz, depending on heart rate.² Time threshold (TTh) is used to discriminate the reflected waves and possible spurious, and represents a reciprocal of the maximum heart rate. The maximum heart rate is estimated on the power spectrum density of the PPG signal. This heart frequency has a half power of the mean heart rate, which contains the maximum power.^20,22 The mean heart rate is located on the range of 0.8 to 3.0 Hz (50-180 beats/min), that corresponds to normal heart rate.²⁰ Figure 2c shows the mean heart value of the PPG signal obtained on one subject in stand-up position.

On the other hand, the amplitude threshold (ATh) is used to determine the possible location of incident waves on the PPG signal. The PPG first derivative is divided on windows of eight seconds, and ATh is computed on each window by equations (1-2). The optimal windows sizes were selected with experimental test, where the window of eight seconds was the best. These windows can be shifted on the first derivative signal adjacently (0% overlapping) or with 50% of overlapping. Both strategies are evaluated in this work. Consecutive peaks of the first derivative are selected as true peaks, if their amplitudes and time separation are higher than ATh and TTh respectively. The temporal location of the true peaks (P₁) corresponds with any point of the up-slope of arterial pulses, as shown in the Figure 2a & 2b.

$RM{S}_k=\frac{\text{1}}{N}\sqrt{{\displaystyle \sum _{i=\text{1}}^N{y}_i^{\text{2}}}}$   (1)

$AT{h}_k=\{\begin{array}{ccc}RM{S}_k+\text{0}\text{.2}\times RM{S}_k,& for& k=\text{0}\\ & & \\ \frac{AT{h}_{k-\text{1}}\times RM{S}_k}{RM{S}_{k-\text{1}}},& for& \text{0}<k<W-1\end{array}$   (2)

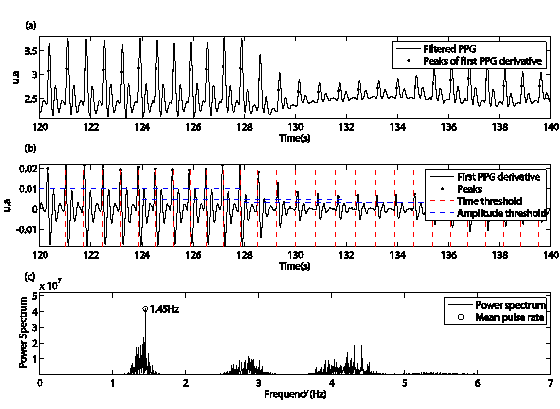
Figure 2 Representation of the proposed method for pulse segmentation, a) black points show a temporal location of maximum of the first derivative, b) discontinue horizontal and vertical traces are the amplitude and time threshold respectively. Vertical traces are the minimal distance necessary between successive peaks.

where y is a first derivative signal, W is the total number of windows of eight seconds (k=0, 2, 3, ..., W-1), N is the total number of samples of each window, RMS and ATh are the root mean square and amplitude threshold of the k window respectively.

Onset decision stage

This stage is based on triangle areas method for determining the pulse onset of each waveform. This method has been used for automatic detection of the beginning and the end points of T wave in the electrocardiographic signal.²⁷ It is based on recursive areas computation of family triangles formed by two fix vertices (P₁ and P₂) and one mobile vertex (P₃) located on the arterial pulse trace. Figure 3 shows the principle of triangle areas method. The vertex P₁ is determined by pulse delineator block from the peak values of the first derivative of pulse waves. To represent the P₂ vertex before P₁, it was considered the same time interval used by Zong et al.²⁸ The authors considered a time interval between the R peak and arterial pulse wave around to 200 ms, to evaluate the accuracy of their proposal. A suitable routine is used to compute triangle areas for different positions of P₃ between P₁ and P₂. The P₃ vertex which produces the highest triangle area is considered as pulse onset. The following expressions (3-5) are used in triangle areas algorithm.

$d_{ \text{ij} }= \sqrt{ {\left(P_{ \text{iX} }-P_{ \text{jX} }\right)}^{ \text{2}}+ {\left(P_{ \text{iY}}-P_{ \text{jY} }\right)}^{ \text{2}}}\begin{array}{cc},& i\ne j\end{array}$   (3)

$sp= \frac{1}{2} {\displaystyle \sum _{i=1}^2 {\displaystyle \sum _{j=2}^3{d}_{ ij }}}\begin{array}{cc},& i\ne j\end{array}$   (4)

$A= \sqrt{sp \left( sp-d_{1\text{2}} \right) \left( sp-d_{\text{13}} \right) \left(sp-d_{\text{23}}\right)}$   (5)

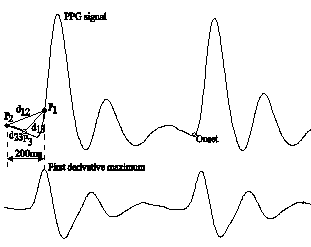
Figure 3 Triangle area method: upper trace is the PPG signal with two consecutive periods; lower trace is the first derivative of the PPG signal; P₁, P₂, P₃ are the triangle vertex.

where P₁, P₂ and P₃ are the triangle vertex, P_iX and P_iY (i=1,2,3) are the abscises (number of samples) and ordinates (arbitrary units) respectively, d₁₂, d₁₃ and d₂₃ are the lengths of triangle sides, sp and A are the semi-perimeter and triangle area, respectively.

Experimental protocol

Seven volunteer subjects, four males and three females were selected to participate in the experimental protocol and provide informed consent in accordance with institutional policy. Personal and clinical data were collected to each subject previous to tests. The mean values of the age and vital signs (heart rate, systolic blood pressure, diastolic blood pressure, breath) of each subject were 19.3 ± 1.50 years, 76.57 ± 9.36 bpm, 109 ± 8.54 mmHg, 67.14 ± 7.47 mmHg and 18.28 ± 2.21breath/min. An experimental station was used to collect the physiological signals of each subject. This station has a simple electrocardiography (ECG) channel and two PPG channels, with bandwidth of 0.15 to 150 Hz and 0.5 to 16 Hz, respectively. All channels were acquired at 1000 samples/s. Initially, each subject remains in rest during five minutes from supine position. Following, ECG and PPG signals were acquired under the same conditions during 5 minutes. Later, the subject goes to stand-up position with the arms nearby the body and remains in rest during 5 minutes. Finally, ECG and PPG signals were acquired from stand-up position during 5 minutes.

Quantitative evaluation

For testing the proposed method simultaneous ECG and PPG signals were manually annotated by trained observers twice. These signals were digitally plotted by a software tool, which provides additional capabilities to add move and remove the fiducial points of the ECG and PPG signals. Previous to the annotations by observers, the PPG signals were filtered with a low-pass filter used in pre-processing stage of proposed method (Butterworth, 2^th order, cut frequency: 16Hz, zero phase).

First, only one of the authors annotated the peak of each QRS complex on ECG signals. Later, two observers annotated on the PPG signal the pulse onsets that correspond to correct peak of each QRS complex. Each observer determined “by eyes” the time location of the pulse onsets throughout the PPG signals. Finally, annotated signals by trained observers were supervised by the same author who annotated the peaks.

Pulse detector on arterial blood pressure signal has been evaluated by Aboy et al.²⁹ They have used open accessible database (Complex Systems Laboratory (CSL) database, http://bsp.pdx.edu) of cardiovascular physiological signals. CSL database has two 60 min records of arterial blood pressure signals. There are three sets of annotations in the database: two by medical experts and the other one by the beat detector proposed by Aboy et al.²⁹ These records were used to evaluate the proposed method, although they do not reflect the artefacts and pathophysiological complexity of arterial blood pressure signals.

Two evaluation parameters, sensitivity (SE) and positive predictivity (+P) were adopted for quantitative evaluation of the proposed delineator. SE indicates the percentage of detected true pulses to overall pulses of arterial blood pressure signals (6), and +P is based on the percentage of detected true pulses to all detected pulses (7). In addition, the failed detection rate was computed by expression (8).

$Sensitivity=\frac{Truepositive}{Truepositive+Falsenegative}\times 100$   (6)

$Positivepredictivity= \frac{Truepositive}{Truepositive+Falsepositive} \times 100$   (7)

$Faileddetectionrate= \frac{Faileddetection}{Numberofonsets} \times 100$   (8)

Evaluation of pulse detection

CSL database was used to evaluate the performance of pulse delineator method. The results were compared with reported systolic peaks (manual annotations and reference detections) in the database. For instance, a threshold of 100 ms was fixed around of manual annotations to admit the delineator results as true positive (TP) or reject them as false positive (FP) or false negative (FN). Furthermore, the records acquired on subjects in supine and stand-up position were used to evaluate the performance of pulse delineator method, too. For this case, threshold of 80 ms was fixed around of pulse onsets annotated by each observer to admit the delineator results as true positive (TP) or reject them as false positive (FP) or false negative (FN).

Fast Fourier Transform (FFT), Welch periodogram and Yule Walker methods were implemented to estimate the time threshold into pulse delineator block and the performance of the three variants were evaluated.

Evaluation of pulse onset detection

The areas triangle method was compared with manual annotations of PPG signals. These signals were acquired on volunteer subjects in supine and stand-up position, and annotated by two trained observers. This strategy had been used in others studies.^19,22,25

The concordance between manual annotations and the proposed method was evaluated by Bland-Altman analysis (Bland and Altman 1986).^5,30 The accuracy of the triangle area method was computed by equation (9) and their results were compared with others methods published as the maximum second derivative, tangent intersection and diastolic point.^18,23 These methods have been reported on several works with different purposes.^13,31,32

$d=\left|x_O-x_A\right|$   (9)

where x_O and x_A are the detection of each observer and algorithm respectively, d is the error value between observers and algorithm A.

The performance of triangle area algorithm was compared in a noisy scenario with the following methods: maximum second derivative, tangent intersection and diastolic point. First, original PPG signals were filtered with low-pass filter (Butterworth, cut frequency: 16 Hz, 10^th order, zero phase). After, the baseline of PPG filtered signals were estimated with elliptic low-pass filter (cut-off frequency: 0.5 Hz, 4^th order), and the variance of baseline was computed. Following, PPG filtered signals were blurred with white Gaussian noise (wgn) to different percentages of baseline variance (5, 10, 15 and 20%). Each level of noise is defined as k condition. Finally, low-pass filter (Butterworth, 2^nd order, cut-off frequency 16Hz, zero phase) was used on the blurred signal and the pulse onset detection methods were applied under the same conditions. Similar methodology has been employed by Xu et al.¹⁹ This process was accomplished under the same k condition (percentage of baseline variance) to several realizations (N=346). To estimate the repeatability of each algorithm for different k conditions, all N sequences x_kn are grouped by two to form all possible sequence x_kn pairs. The total number of M pairs and the difference of each pair are computed by expressions (10) and (11), respectively.¹⁸

$M= \frac{N!}{2! ( N-2 )!}$   (10)

$d_{ mk}= ( x_{ 1mk}(i)- x_{ 2mk}(i) )$   (11)

where x_1mk and x_2mk are the first and second sequence of the pulse onset value of the m^th pair under repeatability k condition, respectively. Furthermore, m=1, 2, 3 … M and i=1, 2, 3 ….R, where R is the number of the periods in arterial pulse wave sequence.

The mean error of the pulse onsets obtained by the same method and under same k condition is calculated as follows:

${\overline{d}}_{mk}= \frac{1}{R} {\displaystyle \sum _{i=0}^{R-1}{d}_{ mk}} (i)$   (12)

The repeatability coefficient of all the m pairs under k condition is computed by the following expression:

$R{C}_{ k}= \frac{1}{M} {\displaystyle \sum _{m=1}^{M-1} \frac{1}{R} \sqrt{ {\displaystyle \sum _{i=0}^{ R-1}{d}_{ mk}} (i)}}$   (13)

These expressions were used by Egidijus et al.¹⁸

Evaluation of pulse delineator

CSL database was employed to evaluate the performance of pulse delineator stage of the proposed method. Table 1 shows that enhanced sensitivity (SE = 99.88 %) and failed detection rate (FDR = 0.44 %) indices respect to Aboy et al.²⁹ algorithm, when overlapped windows of 8 seconds are used to calculate the amplitude threshold value. However, the positive predictivity (+P = 99.69 %) has a small decrease because of the increasing of the number of false positive (erroneous incident waves). The three alternative methods, employed to estimate the time threshold value from power spectral density, obtained equivalent results. The amplitude threshold is estimated with higher adaptability to signal characteristics when overlapped windows are employed, because the current window contains morphologic information about the last window. Smaller windows are more convenient because the morphology of consecutive pulses have a few changes.¹⁹ For this reason, the performance of proposed pulse delineator is better.

Figure 4 illustrates the missing pulse detection of the proposed method and Aboy et al.²⁹ algorithm. Figure 4a shows that the proposed method can detect some pulses failed (false negative) when overlapped windows is employed for computing the amplitude threshold.

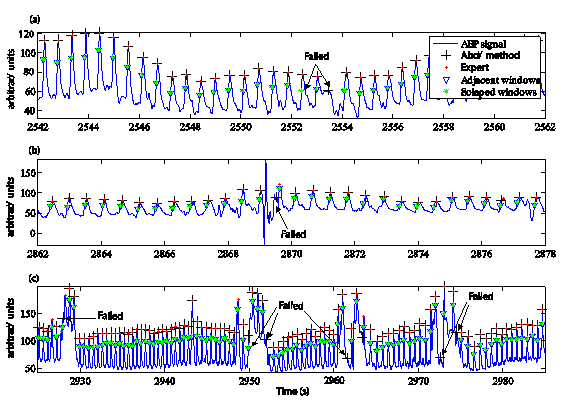
Figure 4 Representation of pulses failed of the proposed method versus Aboy algorithm for the pulses detection, respect to expert criterion. a), b) and c) are intervals of time of the same signal.

Figures 4a to 4c show several failures of pulses detection (false positive) by automatic methods, but the proposed method obtained less miss pulses than Aboy et al.²⁹ algorithm. Furthermore, Figure 4b shows that the estimation of the highest heart rate by power spectral density could reduce the failed detections by artefacts and others morphologic changes of the signal, because the minimum separation (time threshold) between pulses is taken as a reciprocal value of the highest heart rate. Hence, some artefacts between pulses were not detected as true pulses.

Table 2 shows the high values of sensitivity, positive predictivity and failed detection rate of the proposed method for all noise levels. These results are similar to ECG assisted methods (diastolic point, tangents intersection and second derivative). The alternative methods adopted for computing the amplitude and time threshold values obtained a good behavior, but the combination with Welch periodogram obtained the best pulse onset discrimination (SE = 100 %, +P = 100 %, FDR = 0 %). Welch periodogram gives more precision than FFT and Yule Walker to estimate the maximum heart rate on power spectral density, because the overlapped windows allows forming more segments, which can reduce the variance of the estimator and improve its resolution.³³ The performance of proposed method decreased for the signals acquired from stand-up position, because the heart rate and the possibility of artefacts provided by motion sensor increase when the subjects change from supine position to stand-up position. Furthermore, the PPG signal characteristics change a lot. Table 3 shows that the Welch periodogram obtained the best performance (SE = 97.99 %, +P = 97.95 %, FDR = 4.07 %) of all alternative methods with small differences. The results obtained for the alternatives methods are similar to ECG assisted methods.

Evaluation of pulse onset detection

Figure 5 and 6 show the Bland-Altman plot used to demonstrate the degree of agreement between the locations of the pulse onsets determined by different methods. Three combinations were compared: observer #1 versus observer #2, observer #1 versus proposed method, and observer #2 versus proposed method. These figures show a good concordance between the pulse onsets determined by two observers and proposed method. The criterion of the observers was to select the nearest sample to the beginning of the incident wave. Equally, the proposed method search almost always the nearest sample to the beginning of the incident wave, because the mobile point that corresponds to highest triangle area have zero value on the first derivative of PPG.

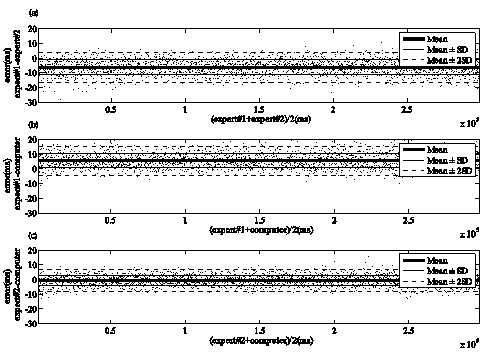
Figure 5 Bland-Altman plot for assessing the concordance of locations of pulse onset marked by two observers and the proposed method in records acquired on subjects from supine position. a) shown the concordance between two observers, b) and c) display the concordance of proposed method with observer #1 and observer #2, respectively.

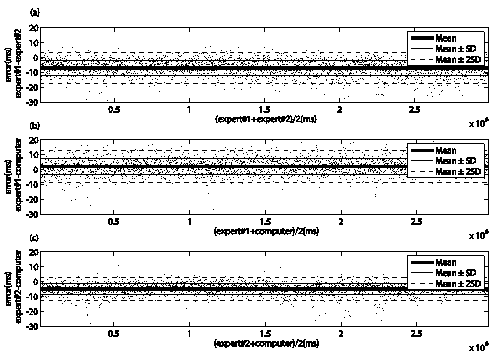
Figure 6 Bland-Altman plot for assessing the concordance of locations of pulse onset marked by two observers and the proposed method in records acquired on subjects from stand-up position. a) shown the concordance between two observers, b) and c) display the concordance of proposed method with observer #1 and observer #2, respectively.

The manual annotations between trained observers have an error of -6.20 ± 4.99 ms and -6.96 ± 5.18 ms for the records acquired on the subjects in the supine and stand-up positions, respectively. The intraobserver error for observer #1 was -0.37 ± 7.97 ms and -0.82 ± 5.69 ms for the records acquired on the subjects in the supine and stand-up positions, respectively. While the other observer has an error of -5.81 ± 5.46 ms and -8.62 ± 5.26 ms for the supine and stand-up position respectively. These errors show an acceptable concordance between observers, and suggest that manual annotations can be used as a reference to evaluate the accuracy and precision of the proposed method.

Table 4 shows the accuracy and precision of proposed method respect to trained observers, and theirs comparison with others assisted algorithms. Triangle area (TA) algorithm obtained the lowest value of error for both positions, while second derivative and diastolic point algorithms obtained the worst accuracy and precision, respectively.

Figure 7 & 8 show the error dispersion intervals obtained by all methods for several noise levels on the PPG records acquired on the subjects in supine and stand-up position, respectively. The error dispersion limits of proposed method not exceed ± 2.9 ms and ± 4.5 ms values with 95% confidence interval, for the lower signal-noise ratio (20% of the variance of baseline), respectively. These values are acceptable, because for several realizations of noise exist a few dispersion of error. Furthermore, the error dispersion of the proposed method is comparable to other methods reported such as tangent intersection. The approach found the repeatability conditions (d_mk mean equal to 0 ± 1.70 ms and 0 ± 3.05 ms) under all signal-noise ratios for both phases of the experiment, supine and stand-up positions. However, the second derivative and diastolic point methods not found the repeatability condition (d_mk mean equal to -0.01 ± 6.13 ms and -1.20 ± 11.15 ms). For second derivative, this condition of repeatability was not significantly different from zero by a Z-test (p = 0.976, α=0.05), but diastolic point was significantly different (p = 0.0456, α=0.05).

Figure 7 ThreeError dispersion at different noise levels in the records acquired on supine position, a) proposed method, b) tangents intersection, c) foot approximation, d) second derivative.

Figure 8 Error dispersion at different noise levels in the records acquired on supine position, a) proposed method, b) tangents intersection, c) foot approximation, d) second derivative.

The proposed method has a good sensitivity, positive predictivity and failed detection rate for different characteristics of signal and several noise conditions. This demonstrates its capability of adaptation throughout the signal. Furthermore, this method has an acceptable accuracy and concordance respect to trained observers. The approach is more convenient than manual method for pulse onset detection, because this automatic method has a highest coefficient of repeatability and accuracy. The performance of proposed method is comparable to others algorithms assisted by ECG. This approach could be used to compute some clinical parameter as pulse transit time, pulse wave velocity, heart rate, heart rate variability and others.³⁴ In addition, it could be used together to other points of interest for derivate some clinical parameter as the relative crest time, reflection index, augmentation index, stiffness index, and others. Furthermore, it could be used in PPG systems of low cost for clinical applications in Health Primary Systems.

None.

None.

The authors declare that they have no competing interests.

1. Hertzman AB. Photoelectric plethysmography of the fingers and toes in man. Proc Soc Exp Biol Med. 1937;37(3):529–542.
2. Allen J. Photoplethysmography and its application in clinical physiological measurement. Physiol Meas. 2007;28(3):R1–R39.
3. Sharkey EJ, Maria CD, Klinge A, et al. Innovative multi-site photoplethysmography measurement and analysis demonstrating increased arterial stiffness in paediatric heart transplant recipients. Physiol Meas. 2018;39(7):074007.
4. Allen J, Zheng D, Kyriacou AP, et al. Photoplethysmography (PPG): State of the art methods and applications. Physiol Meas. 2021;42(10):100301.
5. Radha M, Groot K, Rajani N, et al. Estimating blood pressure trends and the nocturnal dip from photoplethysmography. Physiol Meas. 2019;40(2):025006.
6. Charlton PH, Paliakaitė B, Pilt K, et al. Assessing hemodynamics from the photoplethysmogram to gain insights into vascular age: a review from VascAgeNet. Am J Physiol Heart Circ Physiol. 2021;322(4):H493–H522.
7. Allen J, O'Sullivan J, Stansby G, et al. Age-related changes in pulse risetime measured by multi-site photoplethysmography. Physiol Meas. 2020;41(7):074001.
8. Sulochana CH. A review of photoplethysmography based measurement of blood pressure and heart rate variability. J Bioeng Biomed Sci. 2021;11(1):862.
9. O’Rourke MF. Isolated systolic hypertension, pulse pressure, and arterial stiffness as risk factors for cardiovascular disease. Curr Hypertens Rep. 1999;1(3):204–211.
10. Willum-Hansen T, Staessen JA, Torp-Pedersen C, et al. Prognostic value of aortic pulse wave velocity as index of arterial stiffness in the general population. Circulation. 2006;113(5):664–670.
11. Liang Y, Chen J, Ward R, et al Hypertension assessment using photoplethysmography: a risk stratification approach. J Clin Med. 2018:8(1):12.
12. Nenova B, Iliev I. An automated algorithm for fast pulse wave detection. Int J Bioautomation. 2010;14(3):203–216.
13. Jung D, Kim G, Kim K, et al. Change of pulse wave velocity in arm according to characteristic points of pulse wave. Int Conf Convergence Info Technol. 2007;821–826.
14. Velzen MHN, Loeve AJ, Niehof SP, et al.Increasing accuracy of pulse transit time measurements by automated elimination of distorted photoplethysmography waves. Med Biol Eng Comput. 2017;55(11):1989–2000.
15. London GM, Guerin AP. Influence of arterial pulse and reflective waves on systolic blood pressure and cardiac function. Am J Heart. 1999;138(3 Pt 2):220–224.
16. Nichols WW, Edwards DG. Arterial elastance and wave reflection augmentation of systolic blood pressure: deleterious effects and implications for therapy J Cardiovasc Pharmacol Ther. 2001;6(1):5–21.
17. Sutton-Tyrrell K, Najjar SS, Boudreau RM, et al. Elevated aortic pulse wave velocity, a marker of arterial stiffness, predicts cardiovascular events in well-functioning older adults. Circulation. 2005;111(25):3384–3390.
18. Egidijus KRG, Grcys R, Arunas V. Mathematical methods for determining the foot point of the arterial pulse wave and evaluation of proposed methods. Inform Technol Control. 2005;3:29–36.
19. Hu X, Xu P, Lee DJ, et al. An algorithm for extracting intracranial pressure latency relative to electrocardiogram R wave. Physiol Meas. 2008;29(4):459–471.
20. Chen L, Reisner AT, Reifman J. Automated beat onset and peak detection algorithm for field-collected photoplethysmograms. Annu Int Conf IEEE Eng Med Biol Soc. 2009;2009:5689–5692.
21. Vadrevu S, Manikandan MS. A robust pulse onset and peak detection method for PPG signals analysis system. IEEE Transact Instrument Measure. 2019;68:807–817.
22. Shin HS, Lee C, Lee M. Adaptive threshold method for the peak detection of photoplethysmographic waveform. Comput Biol Med. 2009;39(12):1145–1152.
23. Kyle MC, Klingeman JD, Freis ED. Computer identification of brachial arterial pulse waves. Comput Biomed Res. 1968;2(2):151–159.
24. Mitchell GF, Pfeffer MA, Finn PV, et al. Comparison of techniques for measuring pulse-wave velocity in the rat. J Appl Physiol. 1997;82(1):203–210.
25. Li BN, Dong MC, Vai MI. On an automatic delineator for arterial blood pressure waveforms. Biomed Sig Process Control. 2010;5(1):76–81.
26. O’Rourke MF. Arterial compliance and wave reflection. Arch Mal Coeur Vaiss. 1991;84(3):45–48.
27. García MA, Vázquez CR, Tomàs PJ, et al. An efficient algorithm for onset and offset detection of ECG waves. Fifth Conf Europ Society Eng Med. 1999;383–384.
28. Zong W, Heldt T, Moody GB, et al. An open-source algorithm to detect onset of arterial blood pressure pulses. Comput Cardiol. 2003;30:259–262.
29. Aboy M, McNames J, Thong T, et al. An automatic beat detection algorithm for pressure signals. IEEE Trans Biomed Eng. 2005;52(10):1662–1670.
30. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1(8476):307–310.
31. Xu P, Bergsneider M, Hu X. Pulse onset detection using neighbor pulse-based signal enhancement. Med Eng Phys. 2009;31(3):337–345.
32. Rosenkranz S, Mayer C, Kropf J, et al. Intelligent multichannel sensors for pulse wave analysis. Math Comput Simul. 2011;82(3):483–493.
33. Vijay K, Douglas B. Digital signal processing hand book. CRC Press Inc.Boca Raton. 1997;1–1690.
34. Davies JI, Struthers AD. Pulse wave analysis and pulse wave velocity: a critical review of their strengths and weaknesses. J Hypertens. 2003;21(3):463–472.