Statistical Physics is interested in understanding the macroscopic properties of microscopic activities. The macroscopic properties might be the temperature, representing the system's internal energy, the volume, which is inversely related to the pressure, or the entropy, a measure of the system's disorder. The microscopic activity for this study is the self–assembly of large macromolecules. The macromolecule represents a thermodynamic subsystem, and together with its immediate environment, constitutes an idealized thermodynamic system. This system must obey the statistical laws of thermodynamics: the first law of thermodynamics has to do with the conservation of energy; and the second law has to do with increasing entropy with time. To better understand the molecular self–assembly process, and statistical models of this process, I will be focusing on entropy and the second law of thermodynamics. An important point to note is that when a macromolecule self–assembles, such as the folding of a large protein molecule, the molecule becomes more ordered and the local entropy decreases, however, the entropy of the entire system (molecule and environment) must increase by the second law.

Michael Sprackling in the book “Thermal Physics” stresses the importance of defining the system and processes that science is describing¹. In thermal physics, the ideal system is an isolated whole which contains the matter being studied, and is assumed to be at equilibrium, with state variables, such as temperature, constant. In this study of molecular self–assembly, systems are biological systems, such as the interior of a cell of an organism, and the macromolecules constitute a subsystem. The microscopic process that is being described is molecular self–assembly.

In thermodynamic terms, the process of self–assembly passes from one equilibrium state to another equilibrium state through infinitesimally small steps. This is an ideal condition, and in real microscopic processes equilibrium states blend together, and the state variables change in a continuous way. Sprackling.¹ calls the changing state variables, such as temperature changes, the paths of the process². The thermal states of the system depend on the interactions with the immediate surroundings, as do any entropy changes. Interactions with the environment are important considerations when describing the self–assembly of a molecule, since satisfying the increase in entropy of the second law depends on the environment “absorbing” the entropy increase, while the self–assembly process itself can lead to a more ordered molecule, or a local decrease in entropy.

An important example of molecular self–assembly in biology is protein folding. After protein synthesis has occurred in the cell, the protein macromolecule has completed its chemical synthesis. But if, for example, the protein is going to act as an enzyme, then the final structure is critical for the molecule to perform its catalytic function. The enzyme may require active sites, or pockets, to physically hold the reactants of a biochemical reaction, so the correct folding into this final structure is essential for the function of the enzyme molecule. Thus, modeling and predicting the folding process, and its final structure, is an important problem for thermodynamics to help solve.

The first and second laws of thermodynamics

The first law of thermodynamics refers to the flow of heat in and out, as well as the work done on the system, and this is equivalent to the energy of the system: ΔU = W + Q, where ΔU is the energy transferred to the system, W is the work done on the system, and Q is the heat transferred to the system. The internal energy of a molecule in self–assembly is important, since from the conservation of energy the heat flowing in and out of the molecule, and the work done on the molecule, must occur in such a way to obey the conservation of energy.

Molecular self–assembly must also obey the second law of thermodynamics. The Clausius statement of the second law is that heat flows from the higher temperature to the lower temperature. F.C. Frank had a slogan that “temperature is the mechanical equivalent of entropy³. Wu = –TΔS, where Wu is the ultimate amount of work, T is the absolute temperature in Kelvin, and ΔS is the change in entropy in the system. In real processes, the ultimate work is an ideal that is never reached due to inherent inefficiencies. An alternate definition of the second law comes from the statistical nature of material in the system and the irreversibility of real processes. That is, according to Lord Kelvin, “a process whose only effect is the complete conversion of heat into work cannot occur⁴. When a molecule self–assembles, work is done by the system. The second law states this cannot be done solely by the flow of heat. Entropy can be defined in a statistical way from the large number of molecules in a system: S = k lnΩ, where S is the entropy, k is Boltzmann’s constant, and Ω is the number of possible microstates of the system. The second law becomes dS/dt > 0, where entropy increases with time. F Mandi.² defines the second law of thermodynamics as follows: “During real (as distinct from idealized reversible) processes the entropy of an isolated system always increases. In the state of equilibrium the entropy attains its maximum value⁵.

So, if the second law requires the entropy of a system to increase with time, the system must pass from an ordered state to a disordered state, that is, the number of possible microstates, Ω, increases with time. Self–assembly of a molecule apparently violates the second law since by self–assembly it takes on a more ordered state. The only way this can physically happen is when the self–assembled molecule is considered a subsystem where the entropy decreases, and somewhere else in the system as a whole the entropy increases enough to compensate for this decrease. For a macromolecule this means the local decrease in entropy is kept to a minimal amount, so that the overall maximum value of entropy is kept lower. If the final state of the macromolecule were too “well ordered,” the local decrease in entropy may be too great to be compensated for by the macromolecule’s environment, and by the total entropy increase of the system. This is an important factor in solving for the macromolecule’s final structure.³

Forces at the molecular level

When considering self–assembly of molecules, one has to consider the chemistry, as well as the physics, of the entire system. This is what Barry W Ninham & Pierandrea Lo Nostro.⁴ refer to as linking “structure and function.⁶ What they mean by this is that the geometrical structures and relationships need to be resolved within the physics of the interatomic forces and chemical bonds. Macromolecules have many constituent parts, and any self–assembly is a complex “decision” by the molecule as a whole, with the direction of the self–assembly “decided” by the physics and geometry of the whole, with entropy concerns being only a part of the decision process.

At the molecular level, electrostatic and Van der Waals forces dominate, and these forces are so complex, that a computer simulation of the interactions of a protein molecule “takes up to 30,000 individual … force parameters that depend on temperature.⁷ Exact mathematical solutions are essentially impossible. Even theories and models to understand and simulate large macromolecular interactions are difficult to reconcile with reality. The problem, according to Ninham & Lo Nostro.⁴ has to do with the non–uniformity of the surfaces and interfaces in the macromolecule.⁸ The best tool the biochemist has at this point is thermodynamics and the statistical nature of the large number of parameters at work within the macromolecule. At this level, traditional biology is set aside, and it becomes a problem of physics and chemistry, with the solution being a blend of geometrical structures and models involving statistical physics. Ninham & Lo Nostro.⁴ believe a “paradigm shift is in the procress” with new “theoretical insights” in understanding self–assembly through geometrical models joined to statistical physics.⁹ The authors go on to state that “ideas that focus on entropy vs. hard repulsive forces as the determinants” of phases of some biomolecules is at the “core” of theories developed to explain the biomolecules.¹⁰

Claude Pignet.⁵ in his article “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” suggests the self–assembly of metallo supramolecular complexes can be divided into five free energy contributions.¹¹ He also defines a statistical factor, ω,that measures changes in entropy in the intrinsic rotations of the complex process of self–assembly. The building blocks of the metallo supramolecular complex are a metal and a ligand, with the driving force of the self–assembly being donor atoms on the ligands that connect together¹². Pignet defines finter and fintra as affinities of the binding sites of the inter– and intra– molecular connections. In addition, he defines ω to measure the entropic contributions from the rotational changes that occur when the reactants transform in to the products of the self–assembly. The entropy factor, ω, can be fairly easily calculated “a prior:” ωM.L = (σtotM)* (σtotL)/(σtotML).¹³

The symmetry number of the molecule is σ and affects the rotational entropy of the supramolecule, the factor –Rln(σ).¹⁴ The total symmetry number is the product of the internal and external symmetry numbers, multiplied by mixing entropy that is related to the number of chemical isomers: σtot = σext * σint * σmix.¹⁵ The external symmetry number, σext, comes from the number of possible ways of rotating the molecule as a whole. The internal symmetry number, σint, is defined by the number of ways allowing internal rotations. The correction factor, σmix, is required to account for the chemical isomers, which for the metallo–supramolecular self–assembly comes from the chiral complexes.¹⁶

Once the symmetry numbers, σ, and the resulting statistical factor, ω, are calculated, the free energy of the self–assembled metal ligand supramolecule can be calculated using the following entropy relationship: Δg = –RTln(ωM,L)¹⁷. Physically, this is interpreted as rotational entropy that results from the reactants transforming through self–assembly into the products. Although this change in rotational entropy is small compared to the metal–ligand interactions, the free energy is balanced against the chemical bond breaking and the translational entropy changes. Pignet.⁶ explains there are two principles in action with the supramolecular chemistry of self–assembly:

1. Maximum site occupancy: This maximizes the number of possible metal–ligand connections.
2. Stereochemical matching: This optimizes the specific metal–ligand interactions.¹⁸ These entropy factors of the supramolecules can be used to predict the chemical interactions and geometrical structures of the resulting self–assembled molecule.

The above example of entropy and its role in the self–assembly of supramolecules is typical of supramolecular chemistry. In this chemistry the structural units are held together, not with covalent bonds, but with weaker Van der Waals interactions. Often in these large organic molecules, it is the role of metal donor bonds to hold the organic components of the supramolecule together. The emphasis in supramolecular chemistry is with molecular assemblies, often from non–covalent weaker forces, than with chemical processes involved in the linear progression of chemical reactions.

Another challenge for supramolecular chemistry is to synthesize in the lab what nature does so eloquently in biological systems. Such complex biomolecules as DNA and large proteins, use thousands of molecular connections and can reassemble by storing information electronically in the molecular structure, providing the instructions for self–assembly. Information and entropy play complementary roles in chemical processes. A more ordered state of a physical system provides more information about the system than a less ordered state. The entropy, however, increases when the system becomes more disordered. Entropy is concerned with the direction of physical processes, and less concerned with the energy differences. There is always a trade–off between information and entropy. While a system at equilibrium has entropy at the maximum, less information is available than when the system is in a more ordered state. This balance between information and entropy is important in understanding the physical instructions for supramolecular self–assembly.

Self–assembly in a supramolecule occurs with spontaneous organization, which leads to processes that are reversible, and the errors are easier to correct than with covalent bonds.¹⁹ Another consideration in self–assembly is the role of guest and host, their recognition of each other, and the part entropy plays in this relationship. For entropy, guest and host are subsystems of the combined system. The second law of thermodynamics requires entropy to increase with time. Local decreases in disorder, however, in self–assembled molecules must be made up for in other parts of the guest/host complex as a whole. These changes in entropy are manifested as free energy changes in the overall guest/host structure.

Another perspective on entropy and its role in self–assembly again comes from Claude Pignet, this time in his article “Enthalpy–entropy correlations as chemical guides to unravel self–assembly processes.²⁰” In this article, Pignet.⁶ looks at the relationship between enthalpy and entropy, and how these correlated parameters can give insight into the self–assembly process. He models the intermolecular binding of i ligands B onto the receptor A, where A has n available binding sites. By using the binomial probability density function, the number of possible microstates, Cin, equals n!/(n–i)!i!. Using the van’t Hoff isotherm, the change in free energy ΔG = –RTln(β), where β=Cin(kA,B)I, with kA,B being the microscopic affinity for an A–B connection.²¹ A and B can be generalized to be any receptor/substrate pair, such as found in proteins, ionic solids, or metal–ligands. In free energy change in solution, ΔGA,B = ΔGA,Bdissoc + ΔGA,Bassoc, and the assembly process balances the dissociation, dissolved steps as well as the association steps. Enthalpy and entropy are related in chemical processes by the principle that intermolecular association results in a decrease of entropy (increase in order), ΔSassoc < 0; and the resulting chemical bond has an enthalpy change ΔHassoc < 0. This establishes an enthalpy/entropy correlation H/S. Entropy change at the melting point can be deduced from the melting temperature, Tm, as follows: ΔSm = ΔHm/Tm.²²

¹ “Thermal Physics” pg. 4–8.

² “Thermal Physics” pg. 8–12.

³ “Thermal Physics” pg. 106.

⁴ “Statistical Physics” pg. 31.

⁵ “Statistical Physics” pg. 43.

⁶ “Molecular Forces and Self Assembly in Colloid, Nano Sciences and Biology” pg. 3.

⁷ “Molecular Forces and Self Assembly in Colloid, Nano Sciences and Biology” pg. 6.

⁸ “Molecular Forces and Self Assembly in Colloid, Nano Sciences and Biology” pg. 8.

⁹ “Molecular Forces and Self Assembly in Colloid, Nano Sciences and Biology” pg. 16.

¹⁰ “Molecular Forces and Self Assembly in Colloid, Nano Sciences and Biology” pg. 70.

¹¹ “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” pg. 6209.

¹² “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” pg. 6209.

¹³ “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” pg. 6212.

¹⁴ “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” pg. 6210.

¹⁵ “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” pg. 6214.

¹⁶ “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” pg. 6214.

¹⁷ “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” pg. 6216.

¹⁸ “Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution” pg. 6229.

¹⁹ “Self–Assembly in Supramolecular Systems” pg. 3–4.

²⁰ “Enthalpy–entropy correlations as chemical guides to unravel self–assembly processes” pg. 8059–8071.

²¹ “Enthalpy–entropy correlations as chemical guides to unravel self–assembly processes” pg. 8059.

²² “Enthalpy–entropy correlations as chemical guides to unravel self–assembly processes” pg. 8063.

Entropy plays a significant role in molecular self–assembly as the laws of thermodynamics help determine the path of the assembly process. A good example of this is protein folding. Yuman Arkun & Burak Erman.⁷ define contact order, CO, as “the number of primary sequence bonds between contacting residues in space” based on a 3D topology of the protein structure²³. Low CO structures fold fast, while high CO structures fold slowly. A parameter which goes one step further and takes into account the temporal order of the contacts “a” is called the effective contact order, or ECO. According to these authors, it is the ECO that can be used to understand protein folding mechanisms.²⁴ Using the ECO, they compute entropy loss from certain loop closures, and this determines the path the protein takes in folding. The protein actually surveys the surface and selects the path with low entropy loss. Protein folding is self– assembly so the order increases locally, meaning entropy decreases locally, and ECO is a way to calculate the entropy losses.

The authors of this article, Arkun & Erman.⁷ describe a method to optimize the minimum entropy loss routes; if the protein molecule has enough time to survey the folding routes, it will select the one with minimum entropy loss.²⁵ Natural processes like protein folding take the most efficient path available, and this is with a sequence of contacts that minimizes the entropy loss. The method they describe calculates the entropy loss and selects the most efficient, least loss, route available. Through a series of differential equations, the authors arrive at a mathematical model that describes the minimization of the energy, while avoiding high entropy loss.²⁶ The surface of this mathematical structure is depicted in Figure 1. They then optimize the solution of their differential equation model, which leads to the conclusion that there is a trade–off between the minimization of the energy loss: improving one makes the other worse. They construct a tuning parameter, ρ, that can be adjusted to reflect the above trade–off between energy and entropy.²⁷ This mathematical model is tested with real protein molecules, and ρ is tuned to maintain a desirable rate of decay of entropy. This solution is done in conjunction with the contacts on a contact map. There was some success when predicting how small proteins will fold; the predicted routes by the authors of this article were similar to those observed folding routes in the laboratory.²⁸

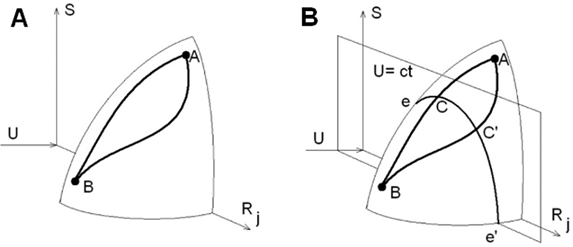
Figure 1 The above diagrams show thermodynamic surfaces that represent folding routes from state A to state B. In panel B, C and C’ have the same energy loss, but the route goes through C because it has smaller entropy loss than C²⁹.

Entropy factors can help in understanding protein folding and the route the protein molecule takes, but how can entropy be used as a predictive indicator?²⁹ How can the understanding of the thermodynamics help in engineering protein structures? Debora S Marks & colleagues.⁸ addressed these issues in the article “Protein 3D structures computed from evolutionary sequence variation.³⁰” They search for predicting protein folding by looking at its past: the evolutionary processes that drive the protein structure in a direction dictated by its function. The goal they set out for themselves in this research is to predict the 3D structure of the protein folding from the sequence of amino acids.

The authors admit the present understanding of protein folding and structures is limited and far from complete, but they have sequencing data and high speed supercomputers to help solve this problem. The set of possible protein configurations is very large, so they develop statistical methods to work with this extensive set of data. They turn to statistical physics and computer science to build a statistical model. The key to their model is the maximum entropy principle, directly from the second law of thermodynamics.³¹

The statistical model they build involves probability models of amino acid sequences. On top of all of the sequencing data and probabilities of amino acid interactions, they impose the maximum entropy condition that maximizes the probability distributions.³² Entropy and its inherent statistical nature is an ideal candidate for constructing a statistical model. This model does a fairly good job of predicting the spatial separations of pairs of contacts. From this they can build a model to predict the 3D structures of the proteins.

They began testing small proteins, and then larger proteins, and achieved good results using the maximum entropy statistical model. Although the test results are difficult to measure, the authors were surprisingly pleased with the accuracy of their model.³³ The results are encouraging enough to believe much more research and improvements can be made in this field. The methods used involved the maximum entropy model to isolate a subset of all possible contact pairs given by the protein molecule. They had successful, but limited, results when applying this model to predict protein folding.³⁴

²³ “Prediction of Optimal Folding Routes of Proteins that Satisfy the Principle of Lowest Entropy Loss: Dynamic Contact Maps and Optimal Control” pg. 1.

²⁴ “Prediction of Optimal Folding Routes of Proteins that Satisfy the Principle of Lowest Entropy Loss: Dynamic Contact Maps and Optimal Control” pg. 1.

²⁵ “Prediction of Optimal Folding Routes of Proteins that Satisfy the Principle of Lowest Entropy Loss: Dynamic Contact Maps and Optimal Control” pg. 1–2.

²⁶ “Prediction of Optimal Folding Routes of Proteins that Satisfy the Principle of Lowest Entropy Loss: Dynamic Contact Maps and Optimal Control” pg. 1–7.

²⁷ “Prediction of Optimal Folding Routes of Proteins that Satisfy the Principle of Lowest Entropy Loss: Dynamic Contact Maps and Optimal Control” pg. 7.

²⁸ “Prediction of Optimal Folding Routes of Proteins that Satisfy the Principle of Lowest Entropy Loss: Dynamic Contact Maps and Optimal Control” pg.8–11.

²⁹ “Prediction of Optimal Folding Routes of Proteins that Satisfy the Principle of Lowest Entropy Loss: Dynamic Contact Maps and Optimal Control” pg. 2.

³⁰ “Protein 3D Structure Computed from Evolutionary Sequence Variation” pg. 1–19.

³¹ “Protein 3D Structure Computed from Evolutionary Sequence Variation” pg. 3.

³² “Protein 3D Structure Computed from Evolutionary Sequence Variation” pg. 3–5.

³³ “Protein 3D Structure Computed from Evolutionary Sequence Variation” pg. 16–17.

³⁴ “Protein 3D Structure Computed from Evolutionary Sequence Variation” pg. 16–17.

None.

None.

1. Michael Sprackling Thermal Physics. Macmillan Physical Science Series, UK 1991.
2. F Mandi. Statistical Physics. John Wiley & Sons, Lt, USA 1971.
3. LF Lindoy, IM Atkinson. Self–Assembly in Supramolecular Systems. The Royal Society of Chemistry, UK 2000.
4. Barry W. Ninham, Pierandrea Lo Nostro Molecular Forces and Self Assembly in Colloid, Nano Sciences and Biology. Cambridge University Press, India 2010.
5. Claude Pignet Five thermodynamic describers for addressing serendipity in the self–assembly of polynuclear complexes in solution. The Royal Society of Chemistry. 2010;46:6209–6231.
6. Claude Pignet Enthalpy–entropy correlations as chemical guides to unravel self–assembly processes. The Royal Society of Chemistry. 2011;40:8059–8071.
7. Yaman Arkun, Burak Erman. Prediction of Optimal Folding Routes of Proteins that Satisfy the Principle of Lowest Entropy Loss: Dynamic Contact Maps and Optimal Control. PLoS One. 2010;5(10): e13275.
8. Debora S Marks, Lucy J Colwell, Robert Sheridan, et al. Protein 3D Structure Computed from Evolutionary Sequence Variation. Plos One. 2011;6(12):e28766.