Seismic denoising is a key step in seismic signal processing for enhancing the resolution of the seismic signal. In this paper, a seismic denoising method is introduced by using variational mode decomposition (VMD) combined with wavelet transform. VMD is used to decompose the seismic data into a series of intrisic mode functions (IMFs) from low frequency to high frequency. Since the noise is always concentrated in the high frequency components, IMFs with high frequency are denoised by using wavelet transform with a soft threshold to effectively remove the noise. Finally, the denoised IMFs and other remained IMFs are reconstructed to form a denoised signal. Synthetic data and real data are used to validate the method.

Key words: seismic signal, variational mode decomposition(VMD), wavelet transform

The suppression of noise in seismic signals is a key preconditioning task in seismic data processing, which relates to seismic signal attribute extraction, data interpretation, and so on.^1,2 In general, seismic noise is divided into two categories, coherent noise and random noise. The occurrence of coherent noise in time has regularity, and random noise does not have a certain law. Nowadays, there are many ways to denoise seismic signals, such as: f-k filter method, wavelet transform method, polynomial fitting method, and KL transformation method and so on.^11–14 However, although these conventional methods suppress the seismic noise successfully, they will produce some false signals or loss of some effective signals, which results in seismic volumes after suppressing noise reducing their fidelity.

Generally, for a smooth and effective signal, the energy mostly concentrates in the low frequency band, only fewer details will appear on the high frequency band. But for a non-stationary noise signal, much of its energy is concentrated in high frequency band.³ VMD algorithm can produce intrisic modes from low frequency to high frequency, which is beneficial to the high frequency signal de-noising separately.

In this paper, a seismic denoising method using VMD combined with wavelet threshold de-noising is proposed. The seismic signals are first decomposed into several intrisic modes by VMD. Then the intrisic modes are transformed into wavelet domain, and the wavelet coefficients are de-noised to obtain the de-noised components. Reconstruction of the components produces a de-noised seismic signal. The method adopted in this paper makes full use of the advantages of VMD and wavelet transform, and suppresses the random noise on the finer scale.

Variational mode decomposition

The VMD algorithm gets rid of the sifting process of the EMD algorithm when the intrinsic mode functions (IMFs) component is obtained.^4-6 The signal decomposition process is transferred to the variational model, and the adaptive decomposition of the signal is realized by searching the optimal solution of the constrained variational model. The frequency center and bandwidth of each component are constantly updated in the iterative solution of the variational mode.⁷ Finally, according to the frequency domain characteristics of the actual signal, the adaptive decomposition of the signal band can be done. In order to estimate the bandwidth of the mode function, the following requirements are required: (1) the analytic signal is computed by the Hilbert transform in order to get to a one-side frequency spectrum. (2) Each mode’s frequency spectrum is shifted to “baseband regions”, by mixing with an exponential tuned to the respective estimated center frequency. (3) The bandwidth of a mode component is estimated through the $H^1$ Gaussian smoothness of the demodulated signal, i.e. the squared $L^2$ -norm of the gradient.⁸ The resulting constrained variational problem is the following:

$\begin{array}{c}\underset{\left\{u_k\right\},\left\{{\omega }_k\right\}}{\min }\left\{{\displaystyle \sum _k{\Vert {\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)*u_k\left(t\right)\right]e^{-j{\omega }_{k}t}\Vert }_2^2}\right\}\\ s.t.{\displaystyle \sum _k{u}_k=f}\end{array}$ ………………… (1)

Where$\left\{u_k\right\}:=\left\{u_1,\mathrm{....},u_k\right\}$ denotes K modes. $\left\{{\omega }_k\right\}:=\left\{{\omega }_1,.\mathrm{..},{\omega }_k\right\}$ Denotes center frequency of K modes.

The above constraint optimization problem can be transformed into an unconstrained optimization problem by using the two penalty term and the Lagrange multiplier.⁸ Then the Lagrange function is introduced:

$L\left(\left\{u_k\right\},\left\{{\omega }_k\right\},\lambda \right):=\alpha {\displaystyle \sum _k\begin{array}{c}{\Vert {\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)*u_k\left(t\right)\right]e^{-j{\omega }_{k}t}\Vert }_2^2\\ +{\Vert f\left(t\right)-{\displaystyle \sum _k{u}_k\left(t\right)}\Vert }_2^2+\langle \lambda \left(t\right),f\left(t\right)-{\displaystyle \sum _k{u}_k\left(t\right)}\rangle \end{array}}$ ……… (2)

The original minimum value problem of Eq. (1) is formulated for using the alternate direction method of multipliers (ADMM) to solve the augmented Lagrange saddle point of Eq. (2), which is the optimal solution of Eq [8].

The steps of the VMD algorithm are as follows:

1. Initialize: $\left\{{\hat{u}}_k^1\right\},\left\{{\hat{\omega }}_k^1\right\},\left\{{\hat{\lambda }}_k^1\right\},n\leftarrow 0$
2. Execute the whole cycle: n $\leftarrow$ n+1.
3. Execute the inner cycle, for k=1:K, update $\left\{{\hat{u}}_k\right\}$ :

$\hat{u}{}_k^1\to \frac{\stackrel{}{\hat{f}\left(\omega \right)-{\displaystyle {\sum }_{i<k}{\hat{u}}_k^{n+1}\left(\omega \right)-{\displaystyle {\sum }_{i>k}{\hat{u}}_k^n\left(\omega \right)+\frac{{\hat{\lambda }}^n\left(\omega \right)}{2}}}}}{1+2\alpha {\left(\omega -{\omega }_k^n\right)}^2}$ ………………… (3)

Update$\left\{\widehat{{\omega }_k}\right\}$ :

$\widehat{{\omega }_k^{n+1}=}\leftarrow \frac{{\displaystyle {\int }_0^{\infty }\omega {\left|\stackrel{}{\widehat{u_k^{n+1}}\left(\omega \right)}\right|}^{2}d\omega }}{{\displaystyle {\int }_0^{\infty }\left|\widehat{u_k^{n+1}\left(\omega \right)}\right|d\omega }}$ ...……….. (4)

Update$\lambda$ :

${\hat{\lambda }}^{n+1}\left(\omega \right)\leftarrow \stackrel{}{{\hat{\lambda }}^n\left(\omega \right)+\tau \left(\hat{f}\left(\omega \right)-{\displaystyle \sum _k{\hat{u}}_k^{n+1}\left(\omega \right)}\right)}$ ……………………. (5)

4. Repeat the processes 2) ~3), until convergence:${\displaystyle \sum _k\left({\Vert {\hat{u}}_k^{n+1}-{\hat{u}}_k^n\Vert }_2^2÷{\Vert {\hat{u}}_k^n\Vert }_2^2\right)<\epsilon }$  

Then the process is stopped and output K narrow ban.

Wavelet threshold de-noising

Wavelet transform, has good time and frequency resolution which makes the wavelet analysis very suitable for time-frequency analysis. With the help of time-frequency local analysis, wavelet analysis theory has become an important tool in signal de-noising. Wavelet threshold de-noising is a kind of wavelet de-noising, which is simple and convenient. Therefore, this paper uses the method to deal with the intrinsic modes after VMD.

The method of implementing the wavelet threshold de-noising method is: (1) transforming the signal into the wavelet domain to obtain the wavelet coefficient; (2) setting a threshold value. Note that the wavelet coefficient smaller than the threshold is considered to be generated by noise and will be removed; (3) the signal is de-noised by reconstructing the processed wavelet coefficients.⁹ The threshold function includes a hard threshold function and a soft threshold function. The hard threshold function is expressed as follows:

${\hat{d}}_{j,k}=\{\begin{array}{l}{d}_{j,k}\left|d_{j,k}\right|>\lambda \\ 0\left|d_{j,k}\right|\le \lambda \end{array}$ …………………. (6)

The soft threshold function is expressed as follows:

${\hat{d}}_{j,k}=\{\begin{array}{l}\mathrm{sgn}\left(d_{j,k}\right)\left(\left|d_{j,k}\right|-\lambda \right)\left|d_{j,k}\right|>\lambda \\ 0\left|d_{j,k}\right|\le \lambda \end{array}$  ……….. (7)

Where, sgn (.) is symbolic function, $d_{j.k}$ is wavelet coefficients, ${\hat{d}}_{j,k}$ is the wavelet coefficient after treatment. $\lambda$ is threshold.
In this paper we use a soft threshold to suppress noise.

Seismic denoising using VMD and wavelet transform

When using the wavelet threshold denoising method to suppress the seismic noise, it weakens a small part of the effective information although most of the noise is suppressed. This fact is caused by the characteristics of the wavelet threshold de-noising method itself.⁹ VMD can decompose the seismic volume into a series of intrinsic modes from low frequency to high frequency adaptively. The seismic noise is generally reflected in the intrinsic modes with high frequencies. We retain the intrisic modes with high frequency by applying wavelet threshold denoising method to them instead of discarding these modes for overcoming high-frequency signal loss problems in the traditional methods. The proposed seismic denoising method using VMD and wavelet threshold de-noising method including the following main steps:

1. VMD is used to decompose the original seismic signal into several intrisic modes from low frequency to high frequency.
2. Wavelet threshold denoising method is applied to the selected intrinsic modes after VMD. VMD can produce one instantaneous frequency for each IMF and form a multitude of instantaneous frequencies from low frequency to high frequency for one seismic signal. Random noise is often distributed in the high frequency components. So here we mainly apply wavelet threshold denoising method to the intrinsic modes with high frequencies to suppress the noise.
3. Reconstructs the denoised signal by using the denoised intrisic modes with high frequencies and those intrisic modes with low frequencies. Since the wavelet threshold de-noising only acts on the high frequency components rather than the whole signal, the proposed method can give a fine effect and overcomes the defects of traditional wavelet de-noising method which suppresses noise to a large extent.^10-14

The synthetic data is superimposed by the Ricker wavelet, and the specific parameters are: the number of acquisition channels is 20 and the sampling interval is 1ms. The synthetic data is shown in Figures 1 shows the synthetic data with noise (signal-to-noise ratio (SNR) =12dB).

Figure 1 Synthetic data.

Then the proposed method using VMD and wavelet transform is applied to the synthetic data with noise in Figure 2. The results are shown in Figure 3. For comparison, the results after wavelet threshold de-noising method for the synthetic data with noise in Figure 4. As can been seen from Figure 3 & Figure 4, these methods are all effective for removing noise. However, the results after the proposed method have less noise interference and are more stable than the wavelet threshold de-noising method.

Figure 2 Synthetic data with noise (SNR=12dB).

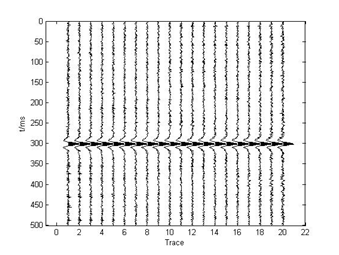
Figure 3 The results after the proposed method.

Figure 4 The results after wavelet threshold denoising.

Here we first use seismic data from a sandstone reservoir in Ordos Basin for analysis. The data is sampled in 2ms. At first, we extract one seismic trace for analysis. Figure 5 shows the seismic data .The IMFs after VMD are shown in Figure 6.

Figure 5 Seismic data.

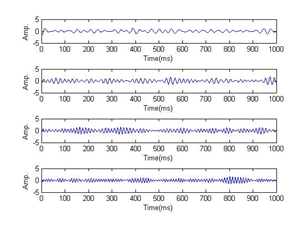
Figure 6 The IMFs after VMD.

As we can see from Figure 6, the seismic data with noise is decomposed into 4 components by VMD, respectively. The frequencies of the third and fourth IMF components are higher, and the waveform has a small number of spikes. Most of the noise in the signal is concentrated in the third and fourth components. Therefore, wavelet threshold denoising method is applied to these components. The results are shown in Figure 7. For comparison, the results after wavelet threshold de-noising method for the seismic data with noise are shown in Figure 8. As can been seen from Figure 7 & Figure 8, these methods are all effective for removing noise. However, from the waveform comparison, we can see that more information is retained after the proposed method. Then, the seismic section is shown in Figure 9, and the IMF sections after VMD are shown in Figure 10.

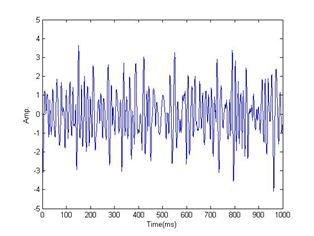
Figure 7 The results after the proposed method.

Figure 8 The results after wavelet threshold denoising.

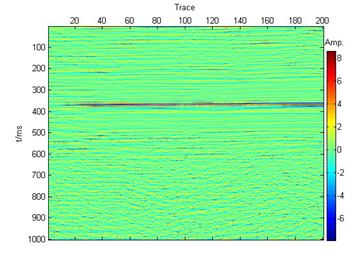
Figure 9 Seismic data from Sandstone reservoir.

As we can see from Figure 10, more information between 300 and 400 ms is clearly visible in IMF1 Figure 10 (a). Sandstone information with less influence is mainly reflected in IMF2 Figure 10(b). Random noise is mainly reflected in IMF3 Figure 10(c) and IMF4 Figure 10(d). Therefore, IMF3 and IMF4 are denoised by using wavelet threshold denoising method. The result is shown in Figure 11. For comparison, the results after wavelet threshold denoising method for the seismic data with noise in Figure 12. As can been seen from Figure 11 & Figure 12, both methods are effective in removing the noise and the results are very obvious. However, the algorithm proposed in this paper makes the noise removed more thoroughly, while the effective information remains intact.

Figure 11 The results after the proposed method. Reconstructed section by IMF1,IMF2.

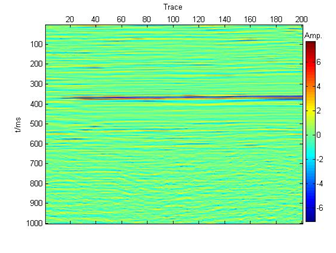
Figure 12 The results after wavelet threshold denoising.

Finally, we use another seismic data for analysis. Figure 13 is the seismic section. The data is sampled in 2ms.

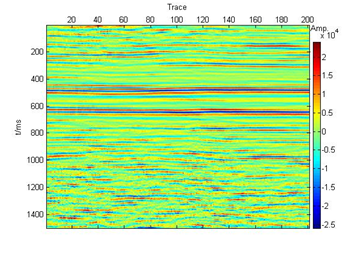
Figure 13 Seismic data from Sandstone reservoir.

The result after the proposed method is shown in Figure 14. For comparison, the result after wavelet threshold de-noising method for the seismic data is shown in Figure 15. As can been seen from Figure 14 and Figure.15, Both methods are effective in removing the noise. However, the algorithm proposed in this paper retains more complete information at the same time.

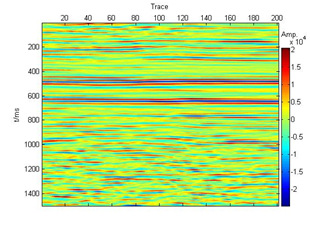
Figure 14 The results after the proposed method.

Figure 15 The results after wavelet threshold denoising.

For suppressing the noise more effectively and adaptively, a method using VMD and wavelet transform is proposed in this paper. The VMD algorithm is used to decompose the original signal into several components with different frequencies. Then, the wavelet threshold de-noising is performed on the IMFs with high frequency which reflect the noise most. The proposed method can suppress a large number of high-frequency noises, while retaining the limited information. Applications on synthetic data and field data show that the proposed algorithm is superior to the conventional wavelet threshold de-noising method. Also, the proposed method is an adaptive method and can retain more effective information and have higher temporal and spatial resolution, and the de-noising effect shows the superiority of the algorithm.

This work was supported in part by the Natural Science Foundation of China under Grants 41404102, in part by Sichuan Youth Science and Technology Foundation under Grant 2016JQ0012, in part by the Key Project of Sichuan provincial Education Department (16ZA0218). The authors also thank for the supportion of SINOPEC Key Laboratory of Geophysics.

The author declares no conflict of interest.

1. Wang Yuying. Seismic Prospecting Signal De–noise Display Technology Research. Petroleum Institution. 2006. p. V1–V8.
2. Zhu Xiaoming. Research of Engineering Seismic Data De–noise Display Technology. Ocean University of China. 2007. p. V1–V14.
3. Han Song. Application of wavelet denoising in Seismic Signal Processing: China Survey and Design. 2016. p. 96–98.
4. Konstantin Dragomiretskiy, Dominique Zosso. Variational Mode Decomposition. IEEE Transactions on Signal Processing. 2014;62(3):531–544.
5. Yanxue Wang, Richard Market, Jiawei Xing, et al. Research on variational mode decomposition and its application in detecting rub–impact fault of the rotor system. Mechanical Systems and Signal Processing. 2015;60:243–251.
6. Yanxue Wang, Richard Market. Filter bank property of variational mode decomposition and its application. Signal Processing. 2016;120:509–521.
7. Soman KP, Prabaharan Poornachandran, Athira S. Recursive Variational Mode Decomposition Algorithm for Real Time Power Signal Decomposition. Procedia Technology. 2015;21:540–546.
8. Bin He, Yanping Bai. Signal–Noise Separation of Sensor Signal Based on Variational Mode Decomposition: IEEE International Conference on Communication Software and Networks. 2016;p.133–134.
9. Zhao Ying, Yue You–xi, Huang jian–liang. CEEMD and wavelet transform jointed de–noising method: Progress in Geophysics (in Chinese). 2015;30(6):2870–2877.
10. K Dragomiretskiy, D Zosso. Variational Mode Decomposition. IEEE Trans. on Signal Processing. 2014;62(3):531–544.
11. Li Kepei, Chen Zhenghua, Sun Yuezhen. Combination F–K filters. Oil Geophysical Prospecting. 1989; p. 359–364.
12. Jiang Tao, Liu Qingpu, Hu Liujun. Research on Wavelet Method of Seismic Signal Denoising. Journal of Harbin Engineering University. 2002; p. 86–90.
13. Zhong Wei, Yang Bao jun, Zhang Zhi. Application of Polynomial Fitting Technique in Strong Noise Seismic Data. Progress in Geophysics. 2006;184–189.
14. Hao Jianhua, Liu Guizhong. Seismic Denoising Method Based on KL Transform on Wavelet Transform Domain. Signal processing. 1997;298–305.