Evolution of the interface between two immiscible fluids is one of the most complicated problems in the fluid dynamics. The major complicity of this problem is due to difficulty of an explicitly closed that describe the interface movement. Parameter h denote the interface position is to deduce the close differential equation for the function
,
and
are the coordinates in horizontal plate,
is the time variable and
is the thickness of the lower fluid.
The behavior of the stratified pair "gas-oil" or "oil-water" natural gas-oil reservoir, can be describe by the thickness of the lower fluid, on the modeling of this function h and then for an optimized recovery, it is absolutely necessary to have an appreciate modeling.1 Whitham2 has considered the case that the viscous force for both fluids can be neglected. Also the case when one of the two fluids is inviscid (like as in water-oil flow investigation in Shallow water theory or ground water flow) have been investigated by Dagan,3 Bear4 and Barenblatt.5 In ground water hydrology, Boussinesq models are involved to describe radial flow from or to well.6,7 Axisymmetric flow is a feature of ground water systems subject to pumping.8,9 Invasion of drilling fluid into a permeable bed is an example of involving pumping problems.10,12 Dussan12 has been investigated the axisymmetric Boussinesq model by similarity variable approach. An early investigation of drilling mud invasion into a permeable aquifer has been provided by Doll.13 Calugaru1 proposed a generalized model for description of evolution of the interface between two immiscible fluids in porous media.
Tang14 studied transient groundwater flow in an unconfined aquifer subject to a constant water variation at the sloping water-land boundary. To characterize the transient groundwater flow, they presented a novel approximate solution to the 1-D Boussinesq equation. They applied the proposed method to various hydrological problems and showed that it can achieve desirable precisions, even in the cases with strong nonlinearity. Bartlet15 introduced a class of solutions of the nonlinear Boussinesq equation with source/sink terms. They applied their new solution to sloping aquifers and analytical results capture hysteresis between the groundwater level and groundwater flow rate as a function of hillslope characteristics. Lu16 suggested a homotopy analysis method (HAM) to solve the generalized Boussinesq equation. Due to the two-degree approximate solution of the variable coefficient Boussinesq equation, they showed that the homotopy perturbation method is effective to solve the variable solution equations. Bansal17 developed a new analytical solution of 2-dimensional linearized Boussinesq equation for approximation of subsurface seepage flow in confined and unconfined aquifers under varying hydrological conditions. He showed that the vertical flow through the base of the aquifer is an important factor in the determination of groundwater mound and cone of depression. Telyakovskiy18 modeled water injection at a single well in an unconfined aquifer by the Boussinesq equation with cylindrical symmetry. By introducing similarity variables, they reduced the original problem to a boundary-value problem for an ordinary differential equation. Their approximate solution incorporated both a singular part to model the behavior near the well and a polynomial part to model the behavior in the far field.
The problem of invasion by drilling fluid into a permeable empty bed solved by Li.19 They used the similarity variable and reduced the axisymmetric Boussinesq equation to a nonlinear ordinary differential equation. Their solution which was a sum of a singular term and a Taylor expansion at the wetting front was demonstrated to be highly accurate. Mortensen20 considered the same problem21 in spherical coordinates with the prescribed power law point source boundary condition. They constructed an approximate similarity solution to a nonlinear diffusion equation in spherical coordinates. In this paper, first, the general dimension equation for interface position between two immiscible fluids in porous media has been presented. Then, the instability of this equation for one dimensional case by considering a self-similar solution and using the perturbation method has been investigated. And finally, an accurate solution to axisymmetric Boussinesq problem has been obtained. Also, in order to describe deformations of the interface separating two immiscible fluids in porous media, a system of partial differential equations which are true on either sides of the interface is required.
Theory
Figure 1 represents the generalized geometry of the problem in an orthogonal coordinate system. The initial position of the interface between two immiscible fluids is identified as initial assumed value of
.When the flow is initiated by a driving force; changes of the interface are specified as a function of space
,
and time
.
Porous media is assumed homogeneous with constant porosity and isentropic. Permeability tensor for such media could be considered a diagonal matrix. By determining the characteristic length of
for horizontal scale and characteristic height of
, the dimensionless equation of changes of the surface could be written as follow [2]:
(1)
(2)
(3)
Where dimensionless parameters are specified as below:
(4)
In these equations subscripts I and II stand for fluid one and fluid two, respectively. In addition, superscript "-" stands for vector quantities and subscript
stands for the ratio of the two similar quantities.
and
indicate the time of propagation of an elastic disturbance, respectively, and the time needed for the media to be filled with gravity flow of the fluid one and
is the characteristic time.
For situations in which the time of propagation of the elastic wave, compared to
, is very short, general Equation 3 could be written as follows:
(4)
(5)
Time and considering the fact that
. Relative time of
would be significantly less than 1. By substituting h for
and eliminating P from the two equations, the system could be revised as a single equation of the coefficient h.
(6)
By substituting
,
and
in a problem containing one fluid with free boundary, Equation (6) could be written as follows:
(7)
One of the applications of Equation (7) is in cases where the height of the porous layer can be considered negligible in comparison to the horizontal length. In such a case
and as a result
can be expressed as a series based on
powers.
In limit conditions, by ignoring the term
, the Equation (7) will turn into the Boussinesq equation.
(8)
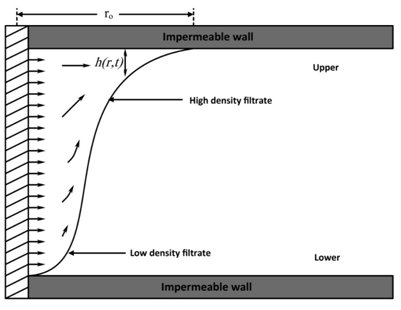
Figure 2 Schematic of diffusion of drilling fluid.
Equation (8) is known as the classic equation of "Shallow Water Flow" theory in porous media. To model the diffusion of drilling fluid in porous media surrounding a circular well (Figure 2), Eq. (8)is given by:
(9)
where
and
is considered to be the characteristic radius. Equation (6) for porous layer with negligible thickness compared to horizontal characteristic length could be indicated as follows:
(10)
This equation points out the position of the interface between two immiscible fluids in porous media with insignificant height compared to its characteristic length, in
and
directions.

Figure 1 Generalized geometry of the problem in an orthogonal coordinate system.
Analyzing the equation and instability
For a one-dimensional flow, Equation (10) changes into a parabolic equation. By considering new independent variable
, following ordinary differential equation (ODE) could be substituted:
(11)
The first point about Equation (11) is attained by investigating the linear stability. By considering
where
a non-disturbance response of the equation is, it could simply be given as:
(12)
(13)
The domain of disturbance and is equal to
. Therefore, to limit the amount of
for infinite time period,
should possess measures below one, in other words,
should be less than
, (
). As a result, if the upper fluid is heavier than the lower fluid, instability phenomenon occurs.
Similarity solution of boussinesq equation
By introducing the similarity variable
and relation
,5 Equation (9) could be written as follows:
(14)
A power-law flux has been considered at the origin where the power is related to the parameter
[5]:
(15)
Dussan12 disclosed that state
indicates filtrate invasion state in special physical problem.
Discusses the problem with constant flux, while
is linearly dependent to the increase in flux with respect to time. With respect to front position
,
is given by:5
(16)
In this paper the "K-method" has been applied to solve the Equation (14) by adding and removing the term
to this equation. The new form of equation would be obtained as follows:21
(17)
(18)
And as for
, f equals 0:
(19)
Where
is the K-method parameter and possesses measures between 0 and 1. For
, response of the Equation (19) and (15) would be the same. With regard to the series
, it could be indicated that:
(20)
or
(21)
By implementing simple mathematical operations, results of the Equation (21) could be defined as three following statements:
(22)
Regarding the Equation (15) the amount of flux accumulation could be written as follows:
(23)
Where C is the constant standing for flux accumulation and equals:
(24)
Thus, characteristic radius
and interface between the two fluids could be indicated with respect to
as follows:
(25)
(26)
Considering the importance of the amount of
in assessing variables of the problem and relations obtained from Equation (21), this integral could be solved with respect to
.
(27)


