
Correspondence:
Received: January 01, 1970 | Published: ,
Citation: DOI:
Download PDF
Abstract
Mass transfer coefficient and diffusion coefficient are important for modeling of food processing operations. There have been many methods to determine mass diffusivity in the during mass transfer phenomena. Drying methods, simplified methods, simulation method, numerical methods, and regular regime method are procedures to determine this parameter. Experimental determination of these parameters would be valuable. This article offers an approach method for estimation of mass transfer parameters (diffusion coefficient (D) and mass transfer coefficient (kc)) using analytical solutions and experimental data for regular geometric shapes such as infinite slab, infinite cylinder, and sphere. Analytical solutions have a broad use in experimentally determining these parameters. Here, the method of Finite Integral Transform (FIT) was used for solutions of governing differential equations. The concentration ratio vs. time of regular shapes was recorded to determine both the mass transfer coefficient and diffusion coefficient. In this study, determination steps of diffusion coefficient during the mass transfer when this parameter is fixed or variable, also been described. The results showed that diffusion coefficients of the sodium tripolyphosphate solutions (2% w/v) in slab shaped before and after the barrier formation on the surface of meat samples was completed is and using the method presented in this paper. In this research, the mass transfer coefficient was also being determined using the analytical solutions when the diffusivity of substance is known.
Keywords: analytical, solutions, mass, transfer, parameters, diffusion, coefficient, finite integral transform
Introduction
Mass transfer is widely used in chemical engineering problems. It is used in reaction separations engineering, reaction, heat transfer, and many other sub-disciplines of chemical engineering. Usually, the difference in chemical potential is the driving force mass transfer. For single-phase systems, this is usually converted to uniform concentration throughout the phase, while for multiphase systems, chemical species often prefers a phase to others and reaches a uniform chemical potential. These mass transfer coefficients are usually published in terms of dimensionless numbers including Reynolds numbers, Sherwood numbers, and Schmidt numbers. The transport of mass in a phase depends directly on the gradient of the concentration of the transport species at that stage.
The mass may be transferred from one phase to another, and this process is called interphase mass transfer.1-3 Based on a theory of mass transfer, the mass transfer rate in the absence of the bulk flow directly proportional to the propulsion is expressed as a molar concentration difference.3 In the two-film theory, the kc is directly proportional to D and inversely proportional to the thickness of the film. In the theory of film propagation, the kc is a complex function of the D, the thickness of the film. In many cases, the kc value cannot be calculated from the basics, although how kc varies according to the operating conditions.1-6 Theoretical expressions for D in a mixture of low-density gases as a function of the molecular properties of the system by Sutherland,7 Jeans8 and Chapman & Cowling9 based on the kinetic theory of gases. Diffusivities of vapors are determined by Winkel Mann10 in which liquid is allowed to evaporate in a vertical glass tube. The diffusion D is not known to transmit another gas and the experimental determination is not practical. It is necessary to use one of the many predictable methods. A normally used method proposed by Gilliland11 and Fuller.12 Different experimental methods for determining the molecular diffusion coefficient. The measurement method is usually included microscopy,13,14 total internal reflection fluorescence (TIRF) spectroscopy 15,16 and Interferometry.17-19 Average balance interface model for equilibrium was developed by Hodgson20 and then improved by Deng.21The convective mass transfer coefficient in the equilibrium interface model introduced by Deng.21,22 To determine the mass transfer coefficient convection (hm), the empirical equations are widely used based on the analytical transfer of heat and mass.21 Mass transfer coefficient (kC) depending on the medium characteristics such as roughness of the surface, mass transfer equipment, shape, the surface temperature, size and profile of fluid flow.23 Different equations in literature have been used to predict mass transfer parameters such as various Sherwood numbers. The reflection of the process parameters experimental determination is important. A novel method for these parameters determination is to use the experimental time-mass concentration data. Analytical solutions of regular shapes such as an infinite cylinder, infinite slab, and sphere with initial and boundary conditions suitable to the experimental data obtained from food material itself may be used to experimentally determine these parameters.23 Therefore, the objective of this study is to explain the methodologies to use analytical solutions of regularly shaped geometries with the experimentally obtained data to determine the mass transfer parameters.
Mathematical modeling
Governing differential equations with initial and boundary condition and solutions for infinite geometries are given by the following equation:
(1)
In the above equation, C is mass concentration; x is the distance from the center of substance; n is a characteristic number (n = 0 for infinitely slab, n = 1 for infinitely cylinder, and n=2 for a sphere); and D is diffusivity coefficient (m2/s). Solutions for Eq. (1), for initial and boundary conditions of central symmetry and convection boundary of the surface, are given for these geometries as follows.24,25
Solution by the method of finite integral transform
A finite integer transform method (FIT) involves an operator that converts the main equation to a simpler domain. The solution in the new domain will be quite primitive. However, to be of practical value, it must be converted into the original space. The operation is formed for this reverse transformation, along with the main operator, which we call a pair of integral transforms.26 to demonstrate the development of the integral transform pair in a practical way, consider the Fick’s mass transfer problem with the regular geometry object. We see the use of the transfer technique as a temporary problem of mass transfer in a slab, cylinder or spherical as shown below:
0<x<1 (2)
According to the initial and boundary conditions:
At t = 0
(3)
At x = 0
(4)
At x = 1
(5)
In the Eq. (2) n is a shape factor of the domain. It takes a value of 0, 1 or 2 for a slab, cylinder or spherical coordinates. Note that the boundary conditions (5) are heterogeneous.
To provide homogeneous boundary conditions, we need to solve the steady-state problem:
(6)
According to:
At x = 0
(7)
At x = 1
(8)
A solution of Eq. (6) is simply. The concentration is equal to:
(9)
Therefore, θ is a new dependent variable. In that sense,
(10)
Substitution of Eq. (10) into Eq. (2), produces the following equations for θ with homogeneous boundary conditions:
(11)
At t = 0
(12)
At x = 0 <
(13)
At x = 1
(14)
This new set of equations can now be easily solved by a finite integral transform method.
The following integral transform is derived as:
(15)
Where the kernel of the transform is obtained from the following associated Eigen problem:
(16)
At x = 0
(17)
at x = 1
(18)
The solution for θ is easily seen:
(19)
And therefore:
(20)
For three different shapes, the expressions for Kn (x), λn, and are:
Slab
(21)
(22)
(23)
(24)
Cylinder
(25)
(26)
(27)
(28)
Sphere
(29)
(30)
(31)
(32)
The dimensionless concentration ratio for non-finite regular geometries is limited to:
Infinitely slab
(33)
Infinitely cylinder
(34)
Sphere
35)
Where
is Fourier number (ξ is L, thickness of half an infinite slab and R, the radius of an infinite cylinder or a sphere); D is the diffusivity coefficient, and the λn are the roots of the following equations (Eqs. (36)- (38)) for infinitely slab, infinitely cylinder and sphere, respectively:25
(36)
(37)
(38)
Where
is Biot number (Bi) and Jo and J1 are the 0th and 1st order of the first kind of Bessel functions, respectively. The mass transfer is obtained by integrating o Eqs. (33) - (35) for the total volume due to the experimental results of mass transfer for the total volume. The results of these integrations for the infinite slab, infinite cylinder, and sphere are obtained by the Eqs. (39) to (41), respectively.
Infinitely slab
(39)
Infinitely cylinder
(40)
Sphere
(41)
As can be seen in Eqs. (39) – (41), it is important to know how many terms of infinite series solutions are necessary to obtain the correct solution. This is a general knowledge that the use of the first term is sufficient if the Fo number is more than 0.2. In this case, the concentration ratio is then linear after that time. This first approach may easily be used to determine this parameter with the value of the mass transfer coefficient (kc).25
Let's assume that the sodium tripolyphosphates concentration were determined in red meat in an experiment for the regular geometries such as infinitely slab, infinitely cylinder and sphere while meat samples were immersed in a solution for a given period of time. It is very easy to determine D as long as the available experimental data when the Fourier number is greater than 0.2. In the following experiment, we measuring the concentration of STP in the beef sample with flat plate shape for determination of constant diffusion coefficient using natural logarithm concentration ratio of STP in the beef vs. time.
Experiments
Analysis of Sodium tripolyphosphate in meat sample with a flat plate shape Sodium tripolyphosphate solution and beef sample were used in this experiment. Therefore, Sodium tripolyphosphate solution must be made before testing begins. Tripolyphosphate solution was prepared using distilled water at 65-70°C. in the various concentrations. Different concentrations of sodium tripolyphosphate solution such as 4%, 6% and 8% (w/v) were used in this experiment. Also, the purchased meat is cut into
mm pieces and used for different stages of testing. It should be noted that the frozen specimens should be melted before testing at room temperature (25-25°C). Beef samples were also immersed in distilled water as a control group. After the preparation of the raw material, the test began several times. To begin each experiment, after cooling the STP solution with desired concentration to ambient temperature, beef samples were immersed in it. The ratio of volume to weight of solutions to beef samples is approximately 5:1(v/w). Then, phosphate level changes in both beef samples and solutions versus time were determined using a modified spectrophotometer ammonium molybdate method. In this experiment, every 10 minutes after immersion, each sample is removed from the solution and the sodium tripolyphosphate concentration is measured. It should be noted that any sample taken out of the solution before measuring the amount of STP in it, first, after leaving their surfaces were washed and dried with a tissue and then they are crushed well in the blender. Five grams of crushed sample was homogeneous in 40 ml of water and allowed to be stored at 4°C for 30 minutes. The homogenous are filtered with a Watten filter paper and then filtered with distilled water to a volume of 50 ml. To do this, a vacuum pump is used. Then, to 5 ml of the filtered sample, 5 ml TAC 10% aqueous solution was added and then centrifuged at 40,000 rpm for 5 minutes. After the supernatant was completed to 25 ml, the pH of the solution was adjusted to 8 using concentrated ammonia solution. Then remove 2 ml of solution and 10 ml combined reagent was added. The volume of this solution reaches 50 ml by adding distilled water. Similarly, at each sampling time, solutions STP phosphate levels were also evaluated. After removing the beef samples, the solution is diluted. The pH of 4 ml of diluted solution is adjusted to 8 and then, 10 ml combined reagent was added, and the resulting solution volume is added to distilled water to 50 ml. The dilution process causes phosphate levels within a measurable range, and by hydrolysis of phosphates into orthophosphates. These mixtures are placed inside the incubator for 10 minutes at a temperature of 37oC. In this experiment, the absorbance was read at 690 nm using UV/VIS spectrophotometry. Also, in order to calculate the concentration of phosphate, the necessary curve was first prepared by standard STP solutions, and then phosphate concentration of samples in term of orthophosphates was calculated using this curve. All of these experiments were repeated 3 times.
Results and discussion
Determination of constant diffusion coefficient value
Suppose that the change in concentration was recorded in a specific location of regular geometries such as an infinite slab, infinite cylindrical shape and spherical object in a medium to determine the diffusion coefficient (D) and mass transfer coefficient (kc). Then, the roots of Eqs. (36)-(38) would be (π/2, 3π/2, 5π/2,….) for an infinite slab, (2.4048, 5.5200, 8.6537,….) for an infinite cylinder and (π, 2π, 3π,….) for a sphere, respectively, when the Bi is infinite. Due to the fact that the concentration ratio
becomes linear when the Fourier number greater than 0.2, the first term of Eqs. (39) to (41), are then used to characterize the linear change in that regions.25 When the natural logarithm of both sides of Eqs. (39) to (41) are taken with the first term approximation (n =1), Eqs. (42) to (44) are obtained for infinite slab (λ1 = π/2), infinite cylinder (λ1 = 2.4048) and sphere (λ1 = π), respectively:
(42)
(43)
(44)
Where A1 in these equations is calculated from the following expressions:
For infinite slab
(45)
For infinite cylinder
(46)
And for a sphere
(47)
As can be seen in Eqs. (42) to (44), slope m of the concentration ratio vs. time curve for the infinite slab, infinite cylinder, and sphere is shown in the following equations:
For infinite slab
(48)
For infinite cylinder
(49)
And for a sphere
(50)
Then, with the known slope and thickness of infinite slab or radius of the infinite cylindrical or sphere materials, the diffusion coefficient (D) value may be determined. As we know, this method does not need to know the location where test data is recorded, regardless of location.27
Diffusion coefficients for the STPs diffusing into the beef samples may easily be determined using these results in both stages before and after the diffusion. After the phosphate content change of the beef samples was experimentally determined, natural log of concentration ratio values
was calculated and graphed versus immersing time. Figure 1 & Figure 2 show this change with respect to the differences in values
in the meat samples before and after the barrier formation was completed. Starting from this point, assuming the natural log of concentration changes after a certain time would be linear, diffusion coefficients may be easily determined with this approach that was applied to the experimental data before and after the barrier formation was completed. As can be seen in Eq. (42), the slope of the concentration ratio versus time directly gives the diffusion coefficient value with the known (Eq. (36). The assumption of an infinite mass transfer coefficient (k) between the surface and the solution interphase was a general approach for this kind of problems. Then, the constant diffusion coefficient of STP in beef with slab shaped may be determined using the following equation:
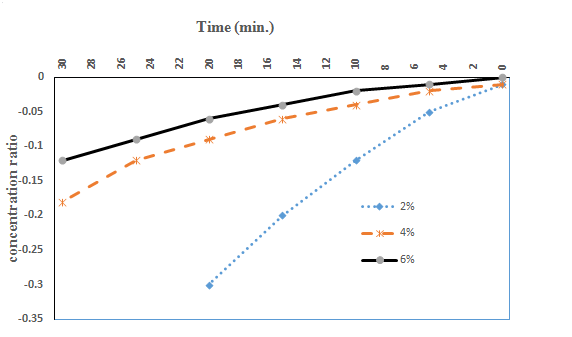
Figure1 The increases in the sodium tripolyphosphate (STP) concentration ratio of the meat samples dipped in STP solutions before the barrier formation was completed.
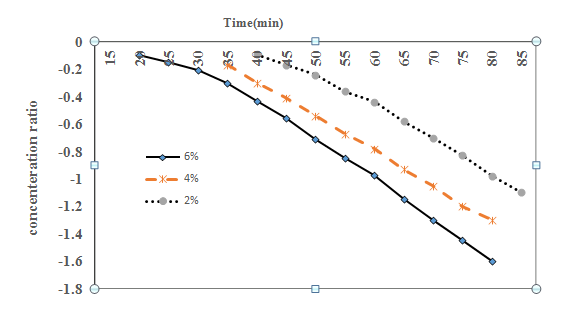
Figure 2 The increases in the sodium tripolyphosphate (STP) concentration ratio of the meat samples dipped in STP solutions after the barrier formation was completed.
Table 1 shows the values of the diffusion coefficient determined according to the concentration of STP solutions. As observed in these results, they increased with increasing concentration of STPs in the early stages of immersing, before the barrier formation was completed. Secondly, after completing the barrier, Diffusion coefficient values have not changed. Minor variations in numerical values may be due to experimental errors.
Concentration of
STP solutions % |
Diffusion coefficient (D) before barrier
formation was completed m2/s |
Diffusion coefficient (D) after barrier
formation was completed m2/s |
2 |
1.81×10-9 |
5.40×10-9 |
4 |
1.99×10-9 |
5.48×10-9 |
6 |
4.00×10-9 |
5.36×10-9 |
Table 1 Diffusion coefficients of the sodium tripolyphosphate solutions for slab shaped before and after the barrier formation on the surface of meat samples was completed (Fo > 0.2)
Determination of average diffusion coefficient
As described above, determining the of diffusion coefficients was based on the assumption that Fourier number is more than 0.2 and the diffusion coefficient of the STPs to be constant through the full immersing process. When the determined diffusion coefficients were used to determine the Fourier number, it is clear that this assumption is not correct. For example, if a 20 mm infinite slab shaped beef sample is immersed in a 2% STP solution, it should take more than 3 hours for this assumption. Although it was thought that after a certain time of immersion, the phenomena of propagation changed. Clearly, the rate of release of STPs and orthophosphates changes through the entire process, leading to a variable diffusion coefficient. The diffusion coefficient values also seemed to be high. When this value was applied to the diffusion equations, the amount of penetration STPs in the meat sample was also determined to be high. According to these problems, another method should be used to determine the minimum mean diffusion coefficient for describing the STP diffusion process. In order to determine the mean diffusion coefficients, the least squares method was used for the experimental data to determine these mean values as the follows:
The results of integration for infinitely slab, infinitely cylinder, and sphere using of Eqs. (33) - (35) through the total volume would be obtained by Eqs. (39) to (41), respectively as the following:
For infinitely slab
(51)
In the above equation, A values in the above equation are given by Eq. (52)
for n= 1,2,…….
(52)
For infinitely cylindrical shape
53)
Where A values in the Eq. (51) are given by Eq. (54):
for n= 1,2,……. (54)
For spherical shape
(55)
Where A values in the Eq. (55) are given by Eq. (56):
for n=1,2,… (56)
In Eqs. (51), (53) and (55), the diffusion coefficient value (D) is only unknown assuming kc of the medium, hence the Bi and the λ values, is known. In this state, the diffusivity (D), the value is determined by solving the above equations. Every other numerical method such as Newton-Raphson may be used to solve this equation. when the Newton-Raphson technique is used, the iterative solution of the Eqs. (57)-(63) give the result of D value for regular geometries:
For infinitely slab
(57)
(58)
For cylindrical shape
(59)
(60)
For spherical shape
<
(61)
(62)
Then, the new diffusion coefficient for any shape is calculated by the following equation:
(63)
In this way, only knowing the concentration ratio at any time will be enough to determine the diffusion coefficient value, instead of using a set of experimental data. Constant D value assumption is checked with this approach using testing data obtained at different times. Table 2 shows the average diffusion coefficients of the sodium tripolyphosphate solutions including 2%, 4% and 6%, (w/v) before and after the barrier formation on the surface of meat samples was completed. As can be seen, the average diffusion coefficient values were found again to increase with increasing STP concentration. Using these values, the diffused amount of STPs into the meat samples may be easily determined.
Concentration of
STP solutions % |
Diffusion coefficient (D) before barrier
formation was completed m2/s |
Diffusion coefficient (D) after barrier
formation was completed m2/s |
2 |
1.76×10-11 |
47.22×10-11 |
4 |
5.57×10-11 |
87.50×10-11 |
6 |
31.82×10-11 |
105.10×10-11 |
Table 2 Average diffusion coefficients of the sodium tripolyphosphate solutions for slab shaped before and after the barrier formation on the surface of meat samples was completed (Fo> 0.2)
Determination of variable diffusion coefficient value
Unal27 published variable diffusion coefficient values for diffusion of sodium tripolyphosphate in red meats. The variable diffusion coefficient may be explained using the above method using Eqs. (57) to (63).
If changes in the entire process continue, it may be simpler to determine an average value for describing the total process, or it should use the numerical finite difference to consider changes. Therefore, to minimize the sum of squares (S), the difference between experimental data and the results of analytical solutions can be used to minimize the equation Eq. (64) as follows:
(64)
In Eq. (64), n is the number of experimentally obtained data, and E is the testing data. The diffusivity value is determined by minimizing S. In the other words should be 0.
Deriving from Eq. (64) relative to D, then the following equations are obtained:
(65)
(66)
From equation (66), this can appear to ∂S/∂D to be 0:
(67)
And the Eq. (67) can be solved numerically for the value of the diffusion coefficient using the Newton-Raphson method or any other solving method.
Constant mass transfer coefficient determination
Mass transfer coefficient can also be determined using the analytical solutions. Therefore, the diffusivity of substance must be known. Then, λ1 is determined
using the slope (m) of the concentration ratio vs time curve. And it is then used to determine the Bi number and thus kc. However, this technique is easy to use. The general approach is to assume in the literature infinity mass transfer coefficient (kc) and then to determine the diffusivity value (D). Nevertheless, can be used the analogy of Chilton-Colburn for determination of the kc and D using heat transfer coefficient when a simultaneous heat and mass transfer is occurring such as drying process:
(68)
Where kc is mass transfer coefficient, h is the heat transfer coefficient, ρ and Cp are density and heat capacity of the heating medium, respectively, Pr is the Prandtl and Sc are the Schmidt number. Essentially, Eqs. (69) to (74) is used to determination of diffusivity value by knowing kc and experimental data. Then, determination of λ value (Eqs. (69), (71) and (73)) and therefore the D value through the slope of the concentration ratio vs. time curve (Eqs. (70), (72) and (74)).
(69)
(70)
(71)
(72)
(73)
(74)
Determining the mass transfer coefficient using a diffusion coefficient is not a simple solution. Therefore, it is assumed that the mass transfer coefficient is known, and then the diffusion coefficient is calculated using the following steps for each of regular geometries such as infinitely slab, infinitely cylinder, and sphere: Determination mass transfer coefficient value from Eq. (68), Determination λ1 value from Eqs. (69), (71) and (73) for infinitely slab, infinitely cylinder, and sphere, respectively, Determination D value from Eqs. (70), (72) and (74) for infinitely slab, infinitely cylinder, and sphere, respectively.
Conclusion
Various methods in literature are described in detail for experimental determining of D and kc. because these approaches require experimental data from interesting materials with analytical solutions. These methods are more advantageous than using preferred methods such as the lumped system approach or use of empirical equations to determine these mass transfer parameters. As seen in these approaches, it is necessary that one of the parameters is known so that another parameter can be determined. Therefore, it is still important to develop a procedure to determine both parameters simultaneously.
In this study, D and kc of regular shapes were estimated using the method of Finite Integral Transform and the experimental data. Diffusion coefficients for the STPs diffusing into the slab-shaped of beef samples may easily be determined using these results before and after the diffusion. Determination of the diffusion coefficient for STPs with the mass transfer coefficient at different stages of the immersion process will be useful for studies on further diffusion and optimization. On the other hand, knowing the degree of penetration of STPs in samples under different conditions leads to useful results in STP in meat. In addition to these, the diffusion coefficient was known to be strongly affected by temperature. In this study, all experiments were accomplished at room temperature (20oC). A small increase in temperature may affect the intensity of the STP release. Therefore, research on the effects of temperature on the release of STP may also be necessary for further studies on this subject.
Highlights
- New approach for determination of mass transfer parameters.
- Using Finite Integral Transform for solutions of governing equations.
- Prediction of constant and variable diffusion coefficient (D).
- Using concentration ratio vs. time for determination mass transfer coefficient and D.
- Determination of mass transfer coefficient, when the diffusivity of substance is known and vice versa
Nomenclature
A: Constant
C: Mass concentration
Ci: Initial mass concentration
C∞: Medium mass concentration
Cp: Specific heat, J/kg-K
D: Diffusion coefficient, m2/s
E: Experimental data
h: Heat transfer coefficient, W/m2K
Jo, J1: The first kind 0th and 1st order Bessel functions
k: Thermal conductivity, W/m K
kc: Mass transfer coefficient, m/s
L: Half-thickness for an infinite slab, m
m: Slopes of concentration ratio vs. time curves, l/s
µ: Dynamic viscosity, kg/ms
θ: Dimensionless mass concentration ratio
θv: Volume average dimensionless mass concentration ratio
r, x: Distance from the center, m
R: Radius of an infinite cylinder or a sphere, m
ρ: Density, kg/m3
ξ: Characteristic length, m
λ: Root of Eqs. (36)-(38)
ν: kinematic viscosity, m2/s
Acknowledgements
The author is grateful to Fars Technological and Environmental Research Center and the Shiraz University of Technology for supporting this work.
Conflict of interest
The author declares that there is no conflict of interest.
References
- Coulson JM, Richardson JF. Chemical Engineering. Sixth edition. USA: Pergamon Press; 1999. 928 p.
- Welty James R, Wicks Charles E, Wilson Robert Elliott. Fundamentals of momentum, heat, and mass transfer. Second edition. Newyork: Wiley; 1976. 789 p.
- Bird RB, Stewart WE, Lightfoot EN. Transport Phenomena. Second edition. Hardcover Publisher; Wiley. 2007. 920 p.
- Taylor R, Krishna R. Multicomponent Mass Transfer. New York: Wiley; 1993.616 p.
- Keith Guillory. CRC Handbook of Chemistry and Physics. USA: CRC Press Online. 2010. 580 p.
- Cussler EL. Diffusion: Mass Transfer in Fluid Systems. Second edition. New York: Cambridge University Press; 1997. 580 p.
- Sutherland W. Phil Mag. 36:507;1894.
- Jeans J. Dynamical Theory of Gases. London; Cambridge University Press; 1921.456 p.
- Chapman S, Cowling TG. Mathematical Theory of Non-Uniform Gases. London: Cambridge University Press; 1959. 423 p.
- Winkle Mann. Diffusion in Gases, Liquids, and Electrolytes. 2017.485 p.
- Gilliland ER. Diffusion coefficients in gaseous systems. Ind Eng Chem. 1934;26(6):681-685.
- Fuller EN, Schettler PO, Giddings JC. A new method for prediction of binary gas-phase diffusion coefficients. In Eng Chem. 1966;58(8):18–27.
- Pappert K, Biesemans J, Clicq D, et al. Measurements of diffusion coefficients in 1-D micro- and nanochannels using shear-driven flows. Lab Chip. 2005;5:1104.
- Kamholz AE, Weigl BH, Finlayson BA, et al. Quantitative Analysis of Molecular Interaction in a Micro fluidic Channel: The T-Sensor. Anal Chem. 1999;71(23):5340–5347.
- Lin Y, Yu X, Wang Z, et al. Measurement of temperature-dependent diffusion coefficients using a confocal Raman microscope with micro fluidic chips considering laser-induced heating effect. Anal Chim Acta. 2010;667(1-2):103–112.
- Foord R, Jakeman E, Oliver CJ, et al. Determination of Diffusion Coefficients of Haemocyanin at Low Concentration by Intensity Fluctuation Spectroscopy of Scattered Laser Light. Nature.1970;227:242–245.
- Swinney K, Markov D, Bornhop DJ. Chip-Scale Universal Detection Based on Backscatter Interferometry. Anal Chem. 2000;72(13):2690–2695.
- Torres JF, Komiya A, Shoji E, et al. Development of phase-shifting Interferometry for measurement of isothermal diffusion coefficients in binary solutions. Laser Eng.2012;50(9):1287–1296.
- Chin LK, Liu AQ, Soh YC, et al. A re-configurable optofluidic Michelson interferometer using tunable droplet grating. Lab Chip. 2010;10(8):1072–1078.
- Little JC, Hodgson AT. A strategy for characterizing homogeneous, diffusion-controlled indoor sources and sinks. ASTM STP.1996. p. 293–304.
- Deng BQ, Tian RX, Kim CN. An analytical solution for VOCs sorption on dry building materials. Heat Mass Transfer. 2007;43(4):389–395.
- Xu Y, Zhang YP. An improved mass transfer based model for analyzing VOC emissions from building materials. Atmos Environ. 2003;37(18):2497–2505.
- Rahman S. Food properties handbook. Boca Raton, FL: CRC Press Inc;1995. 859 p.
- Carslaw HS, Jaeger JC. Conduction of heat in solids. New York: NY: Oxford; 1986. 526 p.
- Erdogdu F. Mathematical approaches for use of analytical solutions in experimental determination of heat and mass transfer parameters. Journal of Food Engineering. 2005;68(2):233–238.
- Rice RG, Do DD. Applied mathematics and modeling for chemical Engineers. John Wiley & Sons Inc. 1995. 396 p.
- Unal B, Erdogdu F, Ekiz HI, et al. Experimental theory, fundamentals and mathematical evaluation of phosphate diffusion in meats. J of Food Engineering. 2004;65(2):263–272.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.




