Physical model
Figure 1 shows the schematic of the ANG storage system for large scale storage which consists of a shell and tube type ANG reactor, NG gas cylinder, two pressure control valves (PCV) and a pump. Through the 3-way valve, the ANG reactor is connected to the gas cylinder during charging process and discharge which is carried out at 1 bar pressure regulated by a pressure control valve. The water present inside the shell is circulated for improving the heat transfer coefficient by using a pump, without any external heating or cooling. The system behaves as a closed system with shell side filled with water. The shell is assumed to be completely insulated from outside and no renewal of the water inside the shell is considered. The water absorbs heat during charging period and supplies the stored heat to the bed during the discharge time. NG is charged into the reactor through the header and subsequently from the header to the tubes through the central porous filter. As shown in Figure 2, square tube layout is considered here. Figure 3 shows the sectional view of the tube with annular portion between the tube wall and inner porous filter filled with a homogeneous mixture of activated carbon and enhancement material (graphite). For the purpose of simulation, the reactor is assumed to be charged with NG at a constant inlet pressure of 35 bar till the bed concentration reaches 0.2 kg/kg. After the charging process is over, the tank is isolated from the supply tank, then it is allowed to reach equilibrium at the corresponding fluid temperature, and subsequently after reaching equilibrium the discharge process is initiated and continued by withdrawing NG at a constant downstream pressure of 1 bar till bed concentration reaches 0.03 kg/kg. After the above process the delivery valve is closed and the bed is allowed to reach equilibrium. To limit the process time and to get a stable cycle the maximum and minimum concentrations are constrained to 0.2 kg/kg and 0.03 kg/kg respectively.

Figure 1 Physical layout.
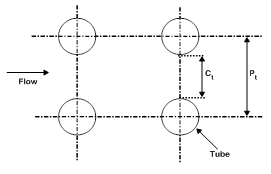
Figure 2 Tube layout.
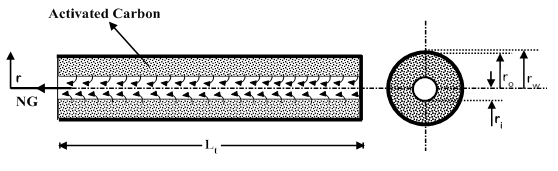
Figure 3 Sectional view of the tube filled with activated carbon.
To simplify the mathematical model, the following assumptions are made:
- Heat transfer through the ANG bed is by conduction in radial direction only, and the gas in the bed is in local thermal equilibrium with the adsorbent particles.
- It is assumed that in order to improve the heat transfer characteristics, the bed is filled with a homogeneous mixture of activated carbon particles and a high thermal conductivity material. It is also assumed that the high thermal conductivity material (graphite) does not adsorb NG.
- The thermo-physical properties of the metal tube and adsorbent are assumed to be constant.
- A constant contact resistance exists between the inner tube wall and ANG bed.
- There is no heat transfer between the bed and NG at the inner radius of the inner tube.
- The thermal energy stored in baffles is not included in the analysis.
- The power consumed by the pump is rejected to the surrounding so that there is no net accumulation of energy in the system
- Based on the above assumptions, the following governing equations are derived.
Tube side heat and mass transfer
Energy equation: The energy equation, derived by writing energy balance equation for an annular differential control volume of the adsorbent bed is given by:
............... (1)
The effective heat capacity and thermal conductivity of the ANG bed (consisting of a homogenous mixture of adsorbent particles, graphite powder and NG in the void space) are given by:
................. (2)
.............. (3)
Where,
; and .................. (4)
“k” is the parameter which accounts for the presence of the graphite powder in the adsorbent bed.
The total porosity of the adsorbent bed is given by:9
............... (5)
The specific heat of the adsorbed phase is given by [18]:
................... (6)
Adsorption isotherm: Among the different isotherm models like Langmuir, Toth , D-R and D-A available in the literature, The Dubinin -Astakhov (D-A) isotherm model is chosen here to calculate the equilibrium adsorption capacity. The D-A isotherm model accounts for surface heterogeneity and also fits well at high pressure.
The D-A isotherm equation is given by:21
..................... (7)
Where va is the specific volume of the adsorbate in the adsorbed phase given by:22
............... (8)
vb is the specific volume of the saturated liquid adsorbate at the normal boiling point, Tb and is the thermal expansion coefficient of the adsorbed phase. The temperature
Dependency of can be approximately expressed as given in equation (9) from the definition of thermal expansion coefficient.23
..................... (9)
Ps is the saturation vapour pressure at the adsorption temperature. When adsorption occurs above the critical temperature, Ps is given by:18
........................ (10)
Equation of kinetics of sorption: The driving force for adsorption rate of gas molecules in adsorbent bed is given by the kinetic equation:24
..................... (11)
Initial conditions: Initially (time, t = 0) the reactor is at ambient temperature (308 K) and the bed pressure is same as ambient pressure (0.1 MPa).
........................ (12)
........................ (13)
............... (14)
..................... (15)
The charging process is continued till the average concentration reaches 0.2 kg/ kg under constant pressure (35 bar) charging condition. After charging process is over the reactor is isolated from the supply tank and is allowed to reach equilibrium state without any further supply of NG from outside. Then the bed is subjected to constant pressure (1 bar) discharge condition till the average bed concentration drops to 0.03 kg/kg. After the discharge process the bed is still allowed to reach equilibrium at corresponding fluid temperature.
Tube side boundary conditions: Assuming adiabatic condition at the inner radius of the adsorbent bed,
.................... (16)
At the outer radius of the adsorbent bed
.......................... (17)
The mass averaged bed temperature and concentration Tavg and qavg are defined as:
..................... (18)
......................... (19)
Energy balance for the tube:
....................... (20)
Where Ai and Ao are the inner and outer area of a single tube respectively.
Initial condition for the tube:
..................... (21)
Shell side calculations: The energy balance for the shell side fluid can be given by:
...................... (22)
Where the total outside heat transfer surface area based on outside diameter of the tube is given by:
............... (23)
Shell side heat transfer coefficient calculation: The length of the tube is fixed at 2.5 m then number of tubes is calculated from the mass of the adsorbent using the following expression:
...................... (24)
Shell diameter is calculated using following expression:25
............................ (25)
Where: .......... (26)
Equivalent diameter of the shell is defined as:
......................... (27)
Bundle cross flow area:
................................. (28)
Where baffle spacing B is taken as 0.6 Ds and .25
Shell side mass velocity:
..................................... (29)
The shell side heat transfer coefficient for external fluid is calculated using McAdams correlation given below:25
(for
)................ (30)
For no circulation case it is assumed that:
................. (31)
In the above correlation is the viscosity of external fluid calculated at wall temperature and is the viscosity of external fluid calculated at mean fluid temperature.
Shell side pressure drop calculation: The pressure drop on the shell side is calculated by the following expression:25
.......................... (32)
Where: ................... (33)
(Nb+1) is the number of times the shell fluid passes the tube bundle and Nb is the number of baffles.
The friction factor f is calculated from
for .................. (34)
The energy input to the pump required for the circulation of water for a complete cycle is calculated using following formula:
............................. (35)
To simplify the calculation it is assumed that the power input to the water by the pump got dissipated by friction and an equivalent amount of heat i.e is lost to the surrounding. So the net energy input to the system is zero. Based on this assumption it can be written that
......................... (36)
All the thermo physical and transport properties of the external fluid (water) are taken from NIST Standard Reference Database 23, Version 9.0.
The performance of the ANG system is indicated in terms of the delivery capacity and effective delivery capacity, given by:
............................. (37)
.......................... (38)
Where Vt is the total tube volume and qavg,i,dis is the average concentration at the start of discharge and qavg,f,dis is the average concentration at the end of discharge. Similarly mg,i,dis and mg,f,dis are the gas mass in the gas space at the beginning and end of desorption respectively. The constant ‘1.5’ is the specific volume of the gas calculated at standard temperature and pressure (STP) (T = 298 K, P = 101.325 kPa). Qd,eff is the effective delivery capacity based on the shell volume.
Second law analysis for the ANG bed for complete charge discharge cycle
The net entropy generated during both charging and discharging of an ANG bed is calculated using entropy balance equation.
............................ (39)
................. (40)
........................... (41)
The entropy change of the adsorbent bed comprising of different parts can be expressed as:
....................... (42)
The change in entropy of the adsorbent (activated carbon) for a complete but stable cycle is expressed as:
.......................... (43)
Similarly the entropy change of the enhancement material (graphite), methane in gaseous as well as in adsorbed form are expressed as given in equations 44, 45 and 46 respectively.
................... (44)
...................... (45)
......................... (46)
.............................. (47)
The specific entropy of the adsorbed phase can be expressed as:18
............... (48)
In the above equation the specific heat of the adsorbed phase, CP,a is replaced by:18
For (T < Tcr)............... (49)
for (T Tcr).................. (50)
For the integration in equation 45, To is taken same as the normal boiling point of methane (111 K) and Po is the normal atmospheric pressure 101.325 kPa. At this reference state the entropy of the adsorbed phase as well as the gaseous phase are assumed to be zero.
The change in entropy of the reactor wall as well as shell side fluid can be expressed as:
........................ (51)
............ (52)
Entropy in and out during the gas exchange process are evaluated using the following expressions:
;Where: ..................... (53)
where: ........................... (54)
......................... (55)
........................ (56)