Introduction: The RT optimization process is based on iterative evaluations, where you find the best treatment aimed to obtain the major TCP without violating pre-established complications for the normal tissues. The optimization can be done varying the values of the imparted dose, number of the fractions or inter-fraction times, which is the method used by the radiobiological (RB) software; or varying the DVHs how is used by the biologically based TPS (BBTPSs) in their IMRT planning inverse modules. The statistical models project (SMp) has proposed new concepts and TCP/NTCP evaluation methodologies aimed to RT optimizations.

Methods: Radiobiological (RB) –probabilistic studies on some current RB concepts and models used for treatment optimization; and the new formulations were done.

Results: 1.- A new SMp cost function involving variables and parameters related to TCP and NTCP; 2.- Detailed description of the uncertainties for a stochastic process/effect SMp type P1; 3.- Some negative aspects were pointed out to the well-known phenomenological models; 4.- The SMp TCP/NTCP models have been considered as probabilistic and mechanistic ones, instead phenomenological/mechanistic; and 5.- Introduction of the new radiobiological concepts that could be used for treatment plan optimization. Some aspects of some current concepts and models used by the BBTPSs were discussed.

Conclusion: The SMp TCP/NTCP calculation methodologies and new SMp concepts can be used in the RT optimizations, for which is essential acceptable formulations for evaluating biological radiation effects (BRE) that are being developed by the SMp.

Keywords: TCP, NTCP, optimization

RB, radiobiological; SMp, statistical models project; BRE, biological radiation effects; OAR, organs at risk; TCP, tumor control probability; NTCP, normal tissue complication Probability; EUD, equivalent uniform dose; DRs, deterministic regions; PFs, probabilistic functions; TV, threshold value; IV, independent variable; SL, sub-lethal; RDD, regional damage distribution; LKB, lyman-kutcher-burman; CDF, cumulative distribution function; PD, poisson distribution; FSUs, function subunits; gEUD, generalized equivalent uniform dose

As the goal of the radiotherapy (RT) is destroying the tumor cells and avoiding the most possible the radiation injuries in the normal tissues and organs at risk (OAR), the optimization of the treatments is aimed to obtaining the major possible tumor control probability (TCP) and the minor normal tissue complication probability (NTCP). When an OAR is irradiated, it will appear one of the possible biological radiation effects (BREs) and later one or more of the possible associated end-points.

Nowadays the Poisson statistics, the effective dose (Deff), the sigmoid curves, equivalent uniform dose (EUD) the TCP Poisson-LQ, NTCP Poisson-LQ and NTCP Lyman are used in the biologically based TPS (BBTPS). Examples of these BBTPSs are: Monaco® V1.0 (CMS/Elekta, Maryland Heights, MO), Pinnacle® V8.0h (Philips Medical Systems, Andover, MA), and Eclipse V10.0 (Varian Medical Systems, Palo Alto, CA). Many of quoted radiobiological (RB) and probabilistic concepts employed by the current RB software and the BBTPSs, represent serious errors and deficiencies in the RT.

Additional to the probabilistic and mechanistic TCP/NTCP models, the statistical models project (SMp) has formulated new cell kill and sub-lethal damage (respectively K and SL) formalisms, which involve all possible factors affecting the biological radiation effects (BRE). These formalisms will allow developing computational simulators aimed to evaluate the TCP/NTCP for RT treatments without using formulas of these indices, but their own probabilistic definitions based on biological radiation effects (BRE) criteria.

The stochastic process/effect should be reported as 0% or 100% in the deterministic regions (DRs), while in the stochastic ones with values into interval [0%; 100%] through probabilistic metrics. As their names indicate, the TCP/NTCP should be modeled with probabilistic functions (PFs), but until date these have not been appropriately modeled because non-probabilistic (mathematical) and/or improper models that have some similarities with the PFs have been used, which has led to some deficiencies and errors. The SMp will provide of pure probabilistic functions, and mechanistic models you will be able to use for describing and predicting experimental/observational datasets. The use of the same type, precise and simple SMp models, will avoid using the current heterogeneous group of non-probabilistic and improper models, as well as correcting some current radiobiological concepts and models.

The habitually-used phenomenological TCP/NTCP model generally is purely a mathematic function or improper PF, which has limitations, deficiencies, or its use represent an error in appropriate descriptions and predictions, mainly out of the regions occupied by the quoted datasets. The tumor control/normal tissue complication are complex stochastic processes, for this reason, the calculations of the TCP/NTCP are possible using techniques, like Monte Carlo simulation. For determining optimized treatments, the evaluation methodologies are used in the iterative calculations of TCP/NTCP aimed to find the major or desired TCP, a minor NTCP and/or without violating a pre-established NTCP. A new cost function has been proposed, which only has dependence of variables and parameters related to TCP and NTCP.

Description of uncertainties of the SMp type P1 stochastic processes/effects

The SMp has classified in three types (P1, P2 and P3) the mean behaviors of following stochastic processes/effects: P1: For values of the independent variable –In RT it is dose that is translated to absorbed energy-<a threshold value (TV) the process is 0%-deterministic, i.e. it will never occur. For values ≥ this threshold, the process is increased when the independent variable (IV) from 0% to 100%, and is stochastic until a determined value of IV where the process becomes 100%-deterministic, i.e. it certainly occurs; P2: For values of IV<a TV, the process is 0%-deterministic. For values ≥ this threshold, the process is increased when IV increases, from 0% to a maximum value, and later it begins to decrease until 0%, at this point the process is 100%-deterministic when IV increases; and P3: For values of IV < a TV, the process is 100%-deterministic. With an increase of IV, it is stochastic and decreases from 100% to 0%, at this point the process is 0%-deterministic when IV increases.

Let us analyze to the SMp cell kill model as one references of SMp models type P1:

$SMp K\left(d\right)=\begin{array}{c}\begin{array}{cc}{\left(\frac{d-dminK}{dmaxK-dminK}\right)}^{pK}& for dminK \le d \le dmaxK\end{array}\end{array}$ (1)

where dminK: Threshold for cell kill.

dmaxK: Minimum dose for a total cell kill.

pK: Power of the SMp K(d) model (pK>0).

 In d< dminK and d>dmaxK the cell kill is a respectively 0% and 100% deterministic effect.

For a determined dose d, the uncertainty in K for a well-defined stochastic region and a uncertainty in pK equal to 2*ΔpK is:

$\Delta K\left(d\right)= {\left(\frac{d-dminK}{dmaxK-dminK}\right)}^{pK+\Delta pK}-{\left(\frac{d-dminK}{dmaxK-dminK}\right)}^{pK-\Delta pK}$ (2)

$\Delta K\left(d\right)=K\left(d\right)*\left[{\left(\frac{d-dminK}{dmaxK-dminK}\right)}^{\Delta pK}-{\left(\frac{d-dminK}{dmaxK-dminK}\right)}^{-\Delta pK}\right]$ (3)

According to Eq. 3, if d=dminK or d=dmaxK, ΔK=0; and ΔK is maximum for d is equal to half point of the interval [dminK; dmaxK]. It can see how the uncertainties for cell survival (ΔS) or ΔK is low for low and high values of d, and larger for values of dose intermediate values in.¹

The behavior of uncertainties for K is shown in the Figure 1, which implies that uncertainties decrease to zero in Xmin and Xmax when the variable X is approached to regions non-stochastic regions NSR1 and NSR2, and viceversa, then in X1/2=(Xmax+Xmin)/2, i.e. half point of the stochastic region there is maximum uncertainty. Given the TCP/NTCP are stochastic processes type SMp P1, the optimal region for tumor control is for high values of its independent variable, where there is high values of TCP and low values of its uncertainties; contrary for NTCP, it is the region for low values of its independent variables.

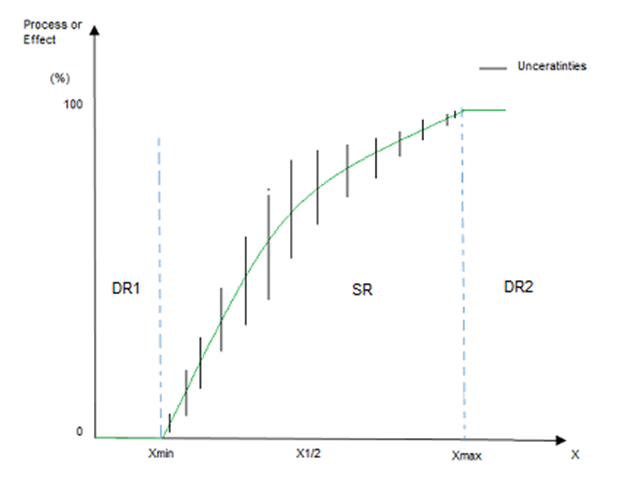
Figure 1 Representation of a mean behavior of stochastic process/effect function of variable X for a SMp type P1 and well-defined SR: Stochastic Region in [Xmin; Xmax] where two DR: Deterministic Regions, the DR1 and DR2 and a stochastic, the SR are pointed out. Only in the SR the process/effect has ranges of values represented by the uncertainties, and likelihood of occurrence between 0 and 100%, while in the DRs have 0% in DR1 and 100% in DR2 without uncertainties. Xmin: Threshold for process/ effect, and Xmax: Minimum value of X for a 100% of process/effect. X1/2 =(Xmax + Xmin)/2, i.e. half point of the SR.

Concepts used in this study

The following definitions and terms that will be used in this study. The five ones are taken directly from.²

Plan optimization or inverse planning: The process of generating an optimal plan following the desired objectives. The planner specifies objectives (i.e., optimization criteria) including constraints (limits that should not be violated) and goals for both the target and normal structures. Internally, the planning system represents these objectives in a cost function, which must be maximized or minimized by an optimization algorithm.

Functional subunit (FSU): Structurally or functionally discrete tissue elements, e.g., nephrons in kidney or alveoli in lung.

Parallel organ: Normal organ in which each FSU functions relatively independently and damage to a sufficiently small region does not render the whole organ dysfunctional. Consequently, a volume threshold or functional reserve may exist. Examples are lung, kidney, and liver.

Serial organ: Normal organ in which FSU are structured in various in a series; if one FSU is incapacitated, the organ will exhibit complications. Examples are spinal cord, intestines, and optic nerve.

Serial and parallel response: Normal organ response characterized by small and large volume dependence, respectively. The connection between organ architecture designated as serial or parallel (see above) and serial or parallel response is not always exact. Nevertheless, within the framework of this report, an exact correspondence between organ architecture and response is assumed. This means that in parallel organs complications are assumed to occur after a substantial fraction of FSUs are damaged, volume effect is large, and response is “parallel.” In contrast, a serial organ would exhibit complications after a single FSU is incapacitated, volume effect is small, and response is “serial.”

Biological radiation effects (BRE): The BRE is defined by the cell kill (K) and cell sub-lethal damage (SL) produced by radiation to a living tissue, represents the mean organ damage. It is applicable to organs, like the liver.

BRE_z: The mean organ superficial damage, the BRE in the plane Z. It is applicable to organs, like the spinal cord.

BRE_L: The mean organ linear damage, the BRE in the circumference L. It is applicable to tube-shape organs, like esophagus.

SMp parallel organ: Normal organ whose complications are evaluated with BRE. Examples are lung, kidney, and liver.

SMp serial organ: Normal organ whose complications are evaluated with BRE, BRE_Z and/or BRE_L. Examples are spinal cord and esophagus

Equivalent cell kill (Keq): It is an equivalent damage to a irradiated living tissue where Keq=BRE(K,SL).

It is very important to consider the expressed and calculated respectively in the following paragraph and equation C2:²” The critical volume or parallel model^3‒6 hypothesizes that NTCP for a parallel-type organ is 0related to the fraction of FSUs that are destroyed by radiation rather than the absolute number of damaged FSUs. The complication occurs when this fraction, denoted the fraction damaged or f_dam, exceeds some critical value referred to as “functional reserve.” For a non-uniformly irradiated organ or tissue, the fraction damaged is calculated according to:

$f_{dam}={\displaystyle \sum _i^n{{}^v}_i}*P\left(D_i\right)$ (4)

where v_i is the fraction organ volume receiving a dose D_i and P(D_i) is the probability of destroying a single FSU following a uniform irradiation with the dose D_i.⁷ In the SMp project the damages for OARs follow the same principle previously quoted concerning the f_dam for the SMp parallel-type organ by means of BRE, while for SMp serial-type organ by means of BRE, BRE_Z and or BRE_L.

The SMp has defined the K and SL for non-uniform dose distributions when a tissue volume V is irradiated with a non-uniform dose distribution and dose per fraction d_i in each fraction of volume v_i, considering a uniform cell density in V, the K and SL for non-uniform dose distributions were obtained as:

$K={\displaystyle \sum _i^n{{}^v}_i}*K_i$ (5)

$SL={\displaystyle \sum _i^n{{}^v}_i}*S{L}_i$ (6)

where n is the number of voxels; v_i is the fraction organ volume receiving a dose d_i. K (d_i) and SL (d_i) are the K and SL associated to a uniform irradiation with the dose d_i. These equations have similarity with the Eq. 4, particularly the Eq. 5. Although K and SL define BRE, the final evaluations of biological damages could be done through an equivalent K (Keq), where Keq ≡ BRE(K,SL).

The SMp has established that there are two ways for the implementation of the TCP and NTCP in the RT:⁸

1. Using the computational-biological RT simulators for calculating TCP/NTCP from the DVH in the ROIs; based on the own probabilistic definitions of these radiobiological indices or
2. Using these as probabilistic and mechanistic SMp TCP/NTCP models with estimated or calculated parameters or obatined from fit of observational datasets.

Modeling and simulation (M&S)

Usually the real data are few, so they do not offer the required information for arriving to precise conclusions about the efficacy or toxicities of treatments, On the other hand the alternative of experiments on animals have high costs. For this reason, the simulation experiments are a good option.

The SMp cell kill and sub-lethal damage formalisms, respectively K(d,n,SL,Rt,(Tk,Pt)) and SL(d,n,SL,Rt,(Tk,Pt)) are function of all factors affecting the biological radiation effects (BRE), d: dose, n: number of the fractions, SL, Rt: cell repair, Tk: time where begin tumor repopulation, and Pt: cell repopulation. They will be useful in the RT/BT treatment simulations, as well as a great potential of the BRE(K,SL) lies in the use of this model together with regional damage distribution to construct cost function for optimization of treatment planning The tumor control (TC) depends of the minimum dose received in a tumor, then the simulations or evaluations for calculating TCP should be done with minimum dose (dminT), and considering the cell repopulation process, so for this evaluation, when K (dminT,n,SL,Rt,(Tk, Pt))=100% there will be TC. In this case, the interest is getting a BRE with a total death of the tumor and the new repopulated cells.

As normal tissue complication depends of the BRE, internal structure and shape of the organ, if it is or not a bilateral organ, its regional damage distribution (RDD), and the specific ubication of BRE. For example, in the spinal cord the complication depends of the radiation affectations in its cross-section area, i.e. the BRE_Z.

The optimization criteria based on biologically related models are potentially more versatile and directly associated with treatment outcome than based on DV criteria. You can optimize the treatments with conjugations of dose (d), number of fractions (n) and the inter-fraction time. If the schedule values (n and d) is varied the optimizations will be like done in Nahum AE⁹ while the variations of the scheme values produce changes in the DVH with associated changes in the BRE and in RDD, then the optimization will be like done by the BBTPSs in their IMRT inverse treatment planning modules. The complications in parallel organ are associated to large BRE with independence of the RDD, while in the other ones, their complications are associated to BRE, BRE_Z and/or BRE_L.

In whatever optimization process, the goal is to find the best treatment with a maximum possible TCP and a minimum possible NTCP, which is obtained by repeated calculations or evaluations of these radiobiological indices, or to do maximum the following cost function:

$\begin{array}{l}SMp F\left(TCP, TC{P}_0,NTC{P}_i,NTCP{0}_i\right)\\ ={\displaystyle \sum }_{i=1}^N\frac{\left(TCP-TC{P}_0\right)}{\left(NTCP{0}_i-NTC{P}_i\right)}*H\left(TCP-TC{P}_0\right)*H\left(NTCP{0}_i-NTC{P}_i\right)\end{array}$ (7)

Where TCP: The calculated TCP.

TCP₀: The desired TCP specified by the user.

NTCP_i: The calculated NTCP for i^th End-point.

NTCP0_i: The inviolable limit of NTCP_i specified by the user.

N: Number of End-points of interest.

H: The Heaviside step function.

The critical element or serial model proposed by the SMp project is premised on a simple argument that if an entire organ composed of FSUs arranged in series its complication is produced when a minimum number of these series or more are broken. By means of the knowledge of the following metrics (BRE_z and BRE_L the BRE in the plane Z and in circumference L, respectively the mean organ superficial and linear damage) the values of the RDD can be characterized in plane Z or a closed-perimeter L.

$BR{E}_z=\underset{A}{{\displaystyle \int }}BRE\left(\overrightarrow{x}\right)d{x}^2$ (8)

Where A is the total number of voxels in the plane z, and $BRE\left(\overrightarrow{x}\right)$ is the BRE in this voxel.

$BR{E}_L=\underset{L}{{\displaystyle \oint }}BRE\left(\overrightarrow{x}\right)dx$ (9)

Where L is the total number of the voxels in the perimeter L, and $BRE\left(\overrightarrow{x}\right)$ is the BRE in this voxel.

Contrary to the optimization in the BBTPSs, where you can characterize the RDD from values of the BRE_z or BRE_L, in the RB software it is impossible, it is advised to work with the worst of the cases, i.e. to consider the minimum vales of the BRE, BRE_A or BRE_L.

The properties of biological cost function proposed by the SMp are summarized in Table 1.

Some radiobiological and probabilistic models and concepts used by the current BBTPSs

The sigmoid curves for characterizing stochastic processes, equivalent uniform dose (EUD) the TCP Poisson-LQ, NTCP Poisson-LQ and NTCP Lyman, and other models and concepts are used by the current BBTPSs. Some of them will be discussed

The equivalent uniform dose: The concept of equivalent uniform dose (EUD) provides a single metric for reporting non-uniform tumor dose distributions. It is defined as the uniform dose that, if delivered over the same number of fractions as the non-uniform dose distribution of interest, yields the same radiobiological effect. To extend the concept of EUD to normal tissues, it was proposed a phenomenological formula referred to as the generalized EUD, or gEUD2:

$gEUD={\displaystyle \sum }_{i=1}{(v_i\text{*}{D}_i{}^a)}^{\frac{1}{a}}$ (10)

Where v_i is the fractional organ volume receiving a dose Di and a is a tissue-specific parameter that describes the volume effect. For a →–∞, gEUD approaches the minimum dose; thus negative values of a are used for tumors. For a →+∞, gEUD approaches the maximum dose (serial organs). For a=1, gEUD is equal to the arithmetic mean dose. For a=0, gEUD is equal to the geometric mean dose.

The mathematic and complex algorithms that process the DVHs through the Eq. 10 do not provide reliable values of gEUD. The experimental determinations of the gEUD have very high costs, and for their determinations with simulation experiments, it is wholly preferable calculating directly the TCP/NTCP. The SMp has formulated TCP/NTCP models using, as referential dose, directly metrics characterizing the DVHs, like the minimum, mean and maximum dose.

TCP and NTCP sigmoid models

The origin of some deficiencies concerning the current NTCP evaluations was the use of Lyman-Kutcher-Burman (LKB) NTCP model, a Normal cumulative distribution function (CDF), which is not a probabilistic function, but is just that its name indicates. The widely used LKB NTCP model is mathematically and computational complex, and has three parameters, where two of them are mathematical. The sigmoid models derived from logistic functions have the same mathematical behavior that LKB has. The Normal CDF has been used for calculating TCP/NTCP as LKB model.² The current sigmoid TCP/NTCP model is a curve with double concavity. Before its inflexion point is a concave upward, while after this is a concave downward. For this model, the manner of TCP/NTCP increases in function of its independent variable in both concavities is different.

The dose-response does not have a sigmoid shape, it has been associated with this shape; because this is own of the LKB and logistic functions, which have habitually been used for fitting these responses.

The SMp has formulated TCP/NTCP probabilistic models that are not sigmoidal.

Poisson distribution

The Poisson distribution (PD) has been used in some TCP models for evaluating the probability of tumor control, while in some NTCP ones for evaluating the complications of FSUs. The SMp has determined that use of the PD in TCP/NTCP models represent an error because: The PD, a limiting case of the Binomial distribution, is unnecessary for characterizing the probability of the RT/BT treatments. You need only to know TCP that is just one of its PD parameters. The use of PD has been done in RT without a correct relationship of PD variables and parameters with the radiobiological concepts.

Relative seriality model

There is not fully serial organ because the organs have their FSUs structured in several series, instead a series. But if it exists, i.e. an organ where its FSUs are structured in a series, then its probability of complications is simply the probability for complication for one FSU, i.e. p, instead the calculated as 1-(1-p)^N, which is the base of the relative seriality NTCP model. When this model uses the PD for evaluating the complications of FSUs, the associated problems increase. The SMp has introduced to new concepts, the SMp serial organ and SMp parallel one, which will be used for evaluating complications in whatever organ.

The complication-free cure (P+) and uncomplicated TCP (UTCP)

The treatments have only efficacy and toxicity associated respectively to TCP and NTCP, and creating new metrics, like the complication-free cure (P+) or uncomplicated TCP (UTCP) could create confusions, because they are mathematic functions involving relationships of these radiobiological indices. For example, the P₊ is defined by pure mathematic operations since TCP and NTCP are related to physical different processes, and there is imprecision in the definition of P₊ as complication-free cure because there is cure without complications when TCP≠ 0% and NTCP=0%.

The mathematic expression that is not associated to real quantities generates virtual metrics. The UTCP and P+ are virtual metrics, and their names related to real probabilistic metrics can generate confusions. The cost function proposed by this study as Eq. 7 can be used with the same role how has been used the metric UTCP.

The optimization of the RT treatments is argued on the complications in SMp parallel organs are associated to large biological radiation effect (BRE) with independence of the regional damage distribution (RDD), while in other organs, their complications can be associated to BRE, BRE_Z and/or BRE_L that represents the damage or reduction of their serial function subunits (FSUs).

The optimization of RT treatments can be included in the developed RT-computational simulators as result of the internal iterative evalutions varying the values of the variable dose (d), and/or some of the parameters that can be varied in a treatment, like the number of the fraction, and the inter-fraction time, i.e. with constant RDD.

For an optimal treatment you should take into account the large uncertainties of the stochastic processes type SMp type P1 is the regions near to half point of the stochastic region, while these are small near to deterministic ones. A new cost function is proposed for the their IMRT planning inverse modules of the biologically based TPSs BBTPSs that only uses values of the TCP, NTCP and desired and pre-established ones respectively. The mathematic and complex algorithms that process the DVHs through the Eq. 10 do not provide reliable values of the generalized equivalent uniform dose (gEUD).

The mathematic expressions that are not associated to real quantities generate virtual metrics. The complication-free cure (P+) and uncomplicated TCP (UTCP) are virtual metrics, and their names related to real probabilistic metrics can generate confusions.

None.

Author declares that there is no conflict of interest.

1. Franken NAP, Oei AL, Petra Kok H, et al. Cell survival and radiosensitisation: modulation of the linear and quadratic parameters of the LQ model (Review). Int J Oncol. 2013;42(5):1501‒1515.
2. http://www.aapm.org/pubs/reports/detail.asp?docid=134
3. Withers HR, Taylor JM, Maciejewski B. Treatment volume and tissue tolerance. Int Journal Radiation Oncol Biol Phys. 1988;14(4):751–759.
4. Niemierko A, Goitein M. Modeling of normal tissue response to radiation: The critical volume model. Int J Radiat Oncol Biol Phys. 1993;25(1):135–145.
5. Yorke ED, Kutcher GJ, Jackson A, et al. Probability of radiation-induced complications in normal tissues with parallel architecture under conditions of uniform whole or partial organ irradiation. Radiother Oncol. 1993;26(3):226‒237.
6. Jackson AR, Kutcher GJ, Yorke ED. Probability of radiation- induced complications for normal tissues with parallel architecture subject to non-uniform irradiation. Medical Physics. 1993;20(3):613‒625.
7. Jackson AR, Ten Haken K, Roberstson JM, et al. Analysis of clinical complication data for radiation hepatitis using a parallel architecture model. Int J Radiat Oncol Biol Phys. 1995;31(4):883‒891.
8. Jang S, Frometa-Castillo T, Pyakuryal AP, et al. The Statistical NTCP and TCP models in the Proton therapy. Medical Physics. 2016;43(6):3451.
9. Nahum AE, Uzan J. (Radio) Biological Optimization of External-Beam Radiotherapy. Computational and Mathematical Methods in Medicine. 2012;2012:4‒13.