Non invasive based patient specific simulation of arteries using lumped models

doi:10.15406/ijrrt.2017.03.00081

International Journal of

eISSN: 2574-8084

Radiology & Radiation Therapy

Research Article Volume 3 Issue 6

Non invasive based patient specific simulation of arteries using lumped models

Bhavya Sambana,¹ Kiran Kumar Y,²

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Prasad RV²

¹Department of Electrical Engineering, India
²Philips Research, India

Correspondence: Kiran Kumar Y, Department of Electrical Engineering, IIT Madras, Chennai, India

Received: April 15, 2017 | Published: August 9, 2017

Citation: Sambana B, Kumar KY, Prasad RV. Non invasive based patient specific simulation of arteries using lumped models. Int J Radiol Radiat Ther. 2017;3(6):306-309. DOI: 10.15406/ijrrt.2017.03.00081

Download PDF

Abstract

This Paper aims at non-invasive prediction of blood pressures and velocities in arteries at any part of the body given the entire physical network of the artery and the blood pressure and velocity values at another point in the artery by constructing the analogous electrical circuit using Windkessel Models. Solving the circuit thus obtained gives blood velocities and also blood pressures at different segments of the artery. These lumped electrical models are validated with ultrasound images of the carotid artery of different patients. Through this method, we can measure the blood velocities and blood pressures in difficult places like brain where much complexity is involved to find the velocities and only the physical network can be found. With the help of these measured values, we can predict rupture of aneurysms using predictive modeling.

Keywords: windkessel, carotid artery, ultrasound, aneurysms

Introduction

Currently, there are no methods available for non-invasive measurement of both blood pressures and velocities through electrical modeling of arteries. Through this method, we can measure hemodynamics such as blood velocities by knowing the physical network of the artery. With the help of the physical network the electrical circuits are stitched all along to the point where there is necessity to find the blood pressures. Based on the values obtained we can predict, when the aneurysm is going to be ruptured or the criticality of the aneurysm.

Python-based simulation of whole physical network is done using Windkessel Models. The physical network given is divided into uniform segments based on radius, with some tolerance. Each segment of the artery is replaced by analogous electrical circuit with current source representing incoming blood velocity. The electrical circuit for each segment is decided based on the diameter, elasticity, thickness of each arterial segment. The obtained electrical circuits are stitched one-one forming a chain of electrical circuits whose impedance can be found, which is used to find the Blood Pressure and Velocities at any segment of the given network. The fact that only ODEs are used to solve hemodynamics may be the reason for lesser accuracy. Our paper has predicted them non-invasively which is a break-through.

Relevant paper work and contributions

Windkessel¹ Model was first designed by German physiologist Otto Frank. He described it as closed hydraulic circuit of heart and arterial system visualizing a water pump connected to chamber,¹ filled with water except for a pocket of air. As the water is pumped, water compresses the air in the pocket and pushes water out of the chamber, which circulates back to the chamber. This is in analogy with the functioning of the heart. The resistance water encounters while leaving the chamber, simulates the resistance(R) which is referred to as Peripheral Resistance(R).²The effect of elasticity of the artery shown on the blood during the blood flow is referred to as Arterial compliance(C).²The inertia of the blood to flow is simulated as Inductance (L).²

Windkessel models (wm)

Windkessel Models are used to model hemodynamic state and estimate the blood flow properties. Frank’s 2 element model (Figure 1) justifies the compliance and resistance offered by the blood. But the 2-element model ignores the inertia of the blood, resistance offered by the aortic valves and wave effect. To solve this a 3-element Windkessel model (Figure 1) was proposed by Westerhorf³-adding a series resistance which simulates the characteristic impedance of the artery and also an Inductance³ element proposed by Gnudi et al.² later modified as 4-element Windkessel model. These models thus help us in prediction of the blood pressures, velocities and diagnosing the complications in the artery. The arterial resistive properties are determined mainly by the small arteries and arterioles, and Compliance(C) is determined mainly by the elastic properties of the large arteries, in particular of the aorta. The lumped models defined in Figure 1 describe the geometry of the artery and flow of blood through three simulation parameters-Peripheral Resistance, Compliance, and Inductance. These parameters are estimated using Poiseuilli’s equation and Bernoulli law with some approximations--Laminar flow, inviscid nature of blood and optimal elasticity of the artery.

Figure 1 Three Windkessel Models.

¹Windkessel¹=Windkessel is a German word for air chamber.

Aneurysm=An aneurysm is an excessive localized enlargement of an artery caused by weakness in the arterial wall.

Methodology

R, L, C values of the above circuits are calculated from the below formulae⁴

$R e s i s t a n c e R = \frac{8 η l}{π R^{4}}$ (1)

l=Length of the arterial segment considered for simulation.

η=Blood viscosity.

R=Radius of the segment (obtained from the ultrasound images using formula).⁵

Blood viscosity is a measure of the resistance of blood to flow, which is being deformed by either shear stress or extensional stress.

$I n d u c t a n c e L = \frac{9 l ρ}{4 A}$ (2)

ρ=Blood Density.

A=Area of Cross Section of the arterial segment.

Inductance measures the inertia of the blood to flow.

$C a p a c i t a n c e C = \frac{3 l π R^{3}}{2 E h}$ (3)

E, h are Elasticity and thickness of arteries respectively.

Units R=mmHgs/cm³

L=mmHgs²/cm³

C=cm³/mmHg

P=mmHg

Q=ml/s

These RLC values obtained from above are in terms of Pa, mmHg .So they are converted to Ohm, Henry and Farad through the following conversions.⁴ Please refer Appendix A for the normal range of cerebral parameters.

0.01ml/Pa=1μF (compliance => capacitance).

1 Pa.s²/ml=1μH (inertia =>inductor).

1 Pa.s/ml=1kΩ (resistance => resistance).

1mmHg=1 volt (pressure =>voltage).

133416ml=1A (volume =>charge).

Input signal

Input Signal: (Supposedly at carotid artery): Amplitude of the signal is varied according to the patient’s blood velocity from the Dicom image.

$f (t) = a m p * (A e^{j ω t} + B e^{2 j ω t} + C e^{3 j ω t})$

A=4-4.5j.

B=3-3j.

C=0.87.

ω=7.54 rad/s.

A, B, C values are decided on trial and error basis to get on to the plot similar to blood pressure/velocity waveform.

The ‘amp’ value is the input velocity and calculated as below:

$a m p = \frac{P S V}{Re (\max (A e^{j w t} + B e^{2 j w t} + C e^{3 j w t}) - \min (A e^{j w t} + B e^{2 j w t} + C e^{3 j w t}))}$

PSV is the Peak Systolic Velocity obtained from the Dicom images and considered as real part of the peak to peak value in the above graph similar to the denominator of ‘amp’. Here after, we mention only the PSV values.

Frequency=72beats/min=1.2beats/s.

ω =2*π*frequency~7.54 rad/s.

Considering the fact that average heart rate of human being is 72beats/min and ω can be varied according to the patient’s data.

Assumptions: Laminar flow, optimal values of elasticity of the artery, inviscid nature of blood are assumed and Poiseuille’s law, Bernoulli principle are used to get to the simulation parameters R,L,C. Linear relationships of R, L, C with physical parameters is assumed and proceeded further. To overcome these assumptions and get very accurate results, we need to find pressure dependence relationships between them and use them in place of these formulae.^1‒3

Implementation

Similar to that of circuit in Figure 2, different combinations of circuits can be stitched according to given arterial segments to obtain the accurate velocities along different points in the artery. Given the whole circuit (blood vessel network), we find the analogous electrical network as shown in Figure 3 ,calculate the total impedance of the network and further divide the flow rates according to each segment’s compliance. Compliance plays a role here, similar to the behavior of capacitor in a circuit of charging and discharging, because of elasticity of blood vessels, blood flow (Q) in arteries also exhibits the similar property like storing of some blood for instant and pumping the rest. So flow rate in a long artery without branching also varies a little because of varying elasticity along the length across each segment. Hence the velocity of blood flow is calculated by dividing Q obtained at each segment with the area of cross section of that segment of the artery.

$V e l o c i t y o f B l o o d F l o w = Q / A$

$F l o w R a t e Q = \frac{V e l o c i t y * π D^{2}}{4}$ (4)

Q= Flow Rate.

A= Area of cross section of the artery.

Figure 2 Plot of Blood Velocity (cm/s) as a function of time(s) on Y-axis and X-axis respectively.

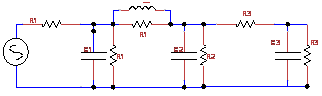
Figure 3 Combination of Different Windkessel circuits-Fig1 are stitched together to get the near approximation of artery segment [5].

Input dicom images

In the demo version of Sante Dicom Viewer we can measure the radius only in pixels. To convert that to centimeters, calibration length of the image is considered and correspondingly a conversion factor is multiplied to get diameter in centimeters.

Conversion (pixels to cm)

$D i a m e t e r (c m) = \frac{C L * (N o . o f p i x e l s m e a s u r e d u s i n g M e a s u r i n g t o o l)}{365}$ (5)

CL is the calibration length, which is 7cm in the image below.

365 is the measured length of the rectangle in pixels where the blood vessel is shown in ultrasound image (Figure 4‒6).

Figure 4 Ultrasound image of Internal Carotid Artery.

Figure 5 Ultrasound Image of Carotid Artery showing the bifurcation of CCA (Common Carotid Artery) into ECA (External Carotid Artery) and ICA (Internal Carotid Artery).

Figure 6 Bifurcation of Carotid Artery and the segments considered for Simulation.

Example:

$D i a m e t e r (D) = \frac{3.0 * 55}{365 * 2} c m = 0.220602 c m$

After getting the input velocity (PSV) from the dicom images, we convert it to flow rate from the formula 4 and as the current flows through the above circuit, flow rate at each segment is calculated and converted back to velocities to get the blood flow velocities.

Similar to the above ultrasound image, 5 images at different points in CCA, ICA, and ECA respectively of the same patient were taken. And velocities at the points L2, L5 and L3 were calculated given velocities at L1 and L4 with ±5% errors based on the flow rate division with different Windkessel models stitched along the artery with the calculated radius from the images and assuming an average elasticity, thickness, viscosities and densities of the blood (Figure 7).

Figure 7 Different Windkessel are stitched to form a circuit.

Results

The tabulated results shows us that the predicted results are very accurate and can thus be used in diagnosis of aneurysms in brain from the estimated blood pressure and velocity values (Tables 1‒3).

Velocity@ L1(cm/s) (CCA)	Est. Velocity at L2	Observed Velocity at L2	Error
116.17	124	121	2.5%

Table 1 Compares the velocities obtained by Simulation (Est. velocity) and the observed velocities from Ultrasound image of CCA
These tables shows the simulated results of a patient.

Velocity at L4(cm/s) (ECA)	Est. Velocity at L5	Observed Velocity at L5	Error
230	108.65	109	-0.3%

Table 2 Compares the velocities obtained by Simulation (Est. velocity) and the observed velocities from Ultrasound image of ECA of the same patient as tabulated in Table 1

Est. Velocity at L3 (cm/s)	Observed Velocity at L3	Error
191.44	192.5	-0.5%

Table 3 Compares the velocities obtained by Simulation (Est. velocity) and the observed velocities from Ultrasound image of ICA of the same patient as tabulated in table I
Using the estimated L2 and L5, velocities at L3 were predicted for 10 different patients which were accurate with less than 5% errors.

Conclusion

In this paper, we have proposed a non-invasive methodology to measure hemodynamics. Simulated results are validated with ultrasound images of patients near carotid arteries and values are accurate up to 5%. Through this method, we can measure the hemodynamics such as blood velocities, in difficult places like brain where much complexity is involved to find the velocities and only the physical network can be found (through angiograms). Based on the predicted velocities, consider an artery with aneurysm, we can detect when the aneurysm is going to be ruptured or the criticality involved and hence pre-diagnosis can be done and patient can be saved before-hand.