The Monte Carlo method was applied using the PENELOPE code to simulate the transport of particles in two different x-ray tubes. This method is considered the most important and accurate for simulations and calculations in different branches of science, including medical physics. The tubes were modeled according to the manufacturer’s specifications, and the simulations were divided into two stages due to the computational time. The scope of the work was to obtain in greater detail photon spectra of different qualities of beams in the orthovoltage range used in radiotherapy, since few works have, yet been developed for this energy range. A detailed analysis was carried out by comparing to the spectra results obtained using the SpekCalc software for the different qualities of radiation in the two stages. Mean energy values along with the first and second half-value layers (HVLs) of each energy were determined with the respective differences between them. Different discrepancies were found in most cases, and so it is vitally important to consider each situation independently. Finally, secondary electron energy spectra in the second stage of each quality were presented with their respective mean energies, an important parameter considered in the dose deposition of the different experimental geometries that use such qualities.

Keywords: radiotherapy, energy spectrum, monte carlo simulations

MC, monte carlo; BIPM, bureau international des poids et mesures; HVLs, half-value layers; LNHB, laboratorie national henri becquerel; IRD, instituto de radioproteção e dosimetria; LNE-LNHB, laboratoire national henri becquerel

Superficial and orthovoltage radiotherapy treatments have been available for many years.^1,2 They use x-ray energies between 50 and 500 kV, making them an effective treatment for superficial tumors, such as skin cancers and keloids.

The study of x-ray spectra is of vital importance for radiation therapy, radiodiagnosis and mammography so that the dose delivered to the patient can be estimated, whether that be during the treatment of some disease or through the process of acquiring an image of a specific region of the body.^3,4 Experimentally, different spectra are obtained, that requires data post-processing dependent on the instrument’s measurement; however, these methods are still inaccessible to some laboratories.^5-7 In the last decades, spectra reported by different groups for different energy bands, following the post-processing of experimentally obtained data,^8,9 have highlighted the degree of difficulty and considerable time of acquisition. Thus, alternative methods to obtain such spectra have also been reported in the literature, some with empirical and semi-empirical approximations, including mixed methods, which require a low computational cost for the calculation.¹⁰ The most accurate of these methods though is the Monte Carlo (MC) method.^11-14

The MC method uses probability functions of the different processes of interaction between radiation and matter, and thus provides, through simulations of such processes, expected values of macroscopic quantities to reach an approximate solution of a problem.¹⁵ That is, this method makes use of statistics and computers to reproduce the behavior of real systems using mathematical models.¹⁶ Although it takes a lot of computation time, modern computers have reduced this time and made this solution feasible.

In contrast, the SpekCalc software is a commercial program widely used to obtain photon spectra in the range between 40 kVp and 300 kVp from specific x-ray tubes with tungsten target for different anode angulations and different combinations of additional filtrations obtained under known conditions as “good geometry”, that is, without scattering. It is based on mixing deterministic equations to calculate the Bremsstrahlung X-ray production together with electron distributions pre-calculated using the MC method.¹⁷

Due to the need to accurately determine different photon spectra in the energy range of orthovoltage radiotherapy, this work used the MC method for radiation transport to simulate electron beams in four qualities defined by the Bureau International des Poids et Mesures (BIPM). The spectra obtained were compared to those of the SpekCalc software. This work was divided into two stages of MC simulations. First, two x-ray tubes were modeled, registering the spectrum for each energy at the exit of both X-ray tubes. Then, different filtrations were simulated for each beam quality, obtaining the spectrum of photons one meter from the target. In this second stage, the first and second half-value layers (HVLs) were calculated using MC simulations and experimental data. Average energy values ​​for each quality were calculated and compared with results from the Laboratorie National Henri Becquerel (LNHB). Finally, spectra of secondary electrons for each quality from the second stage, as well as their average energies were determined, both of which are considered the novelties of this study.

In the first part of this work, two x-ray tubes were modeled for simulation using the PENELOPE code.¹⁸ The simulations were divided into two stages: simulating each tube for different qualities and, simulating the experimental arrangement using different filtrations to obtain the photon spectra at one meter from the source. In the second part of this work, spectra were obtained for different qualities of radiation from one of the modeled tubes and the HVLs of these spectra were calculated.

Monte Carlo (MC) simulations

MC simulations were performed with the PENELOPE code (v. 2018) at the LCR-UERJ cluster. In both stages, different methods of variance reduction were used as well as parallel simulation. The order of magnitude of the number of particles in the primary beam was 10⁹ and 10¹¹ in the first and second stages, respectively. The x-ray tubes of models MXR160 and MXR450 from COMET X-ray¹⁹ were modeled in the Pengeom package following the manufacturer's specifications (Figure 1). The main difference between these tubes is the thickness of the beryllium window, and so MXR160 is represented in Figure 1, as viewed in gview3D and gview2D of the PENELOPE package.

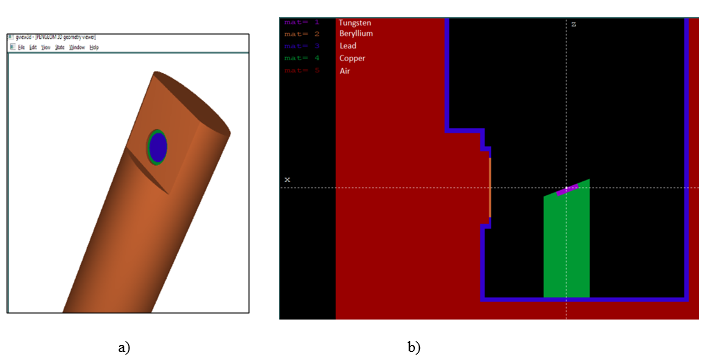
Figure 1 Simulation of the X-ray tube, model MXR160: Beryllium exit window with thickness of 0.8 mm and lead shield. a) 3D view and, b) Y-axis point of view (2D).

Simulations stage 1: The tubes were modeled, and the electron beam was simulated reaching the tungsten. The photon spectra generated at the exit of the beryllium window were recorded. All the geometric details of the tube provided in the manufacturer's specifications were considered using the thick focal point of 5.5 mm in diameter. Every simulation has an air layer involving the region of interest, even the results from SpekCalc software. For each energy, 100 parallel simulations were performed,²⁰ with 10⁷ as the number of histories for each. Interaction forcing and splitting for radiative events were used as methods of variance reduction to optimize the simulation time. A script (executable from the penmain-sum file of the PENELOPE package) was used to condense the parallel simulation results and obtain spectra with reduced uncertainty. The values ​​of the intrinsic transport parameters of the PENELOPE code used in all simulations, such as local absorption energy of particles, cutoff energy for inelastic collision and Bremsstrahlung interaction, were respectively: Eabs=1 keV; C1=C2=0.2; Wcc=10 keV and Wcr=1 keV (see Table 1 for more details). The energy discretization of all spectra was 0.5 keV resolution, thus obtaining several bins for each spectrum equal to twice the peak energy. The different qualities simulated in this work have a nominal energy of 100, 135, 180 and 250 kVp. For the two lowest energies, the MXR160 tube model was used and, for the two highest energies, the MXR450 was used.

Simulations stage 2: By using the spectra obtained from the simulations of stage 1 as inputs for the next stage, different filtrations were simulated as shown in Table 2. The values of aluminum and copper thicknesses, used as additional filters, implemented at the Brazilian National Ionizing Radiation Metrology Laboratory LNMRI²¹ were considered. Along with the additional filter, the beam is collimated by two lead collimators in such a way that at one meter from the source, the field is circular, with diameter equal to 10 cm, that is, the beam was considered as a broad beam.

For each energy, between 50 and 100 parallel simulations were performed, with 5x10⁸ primary particles. The same variance reduction methods were also used and added to the results in parallel with the same script as stage 1. The values of the intrinsic transport parameters did not change in relation to the previous stage. The main feature of the photon beam is that it was always modeled with the same size for the thick focal spot and the same angle of the exit window. In this way, the beam is divergent, projecting a 10 cm diameter of circumference, one meter away from the source after the set of filtrations and collimators, recording the final spectrum through an air detector located in that region (Figure 2).

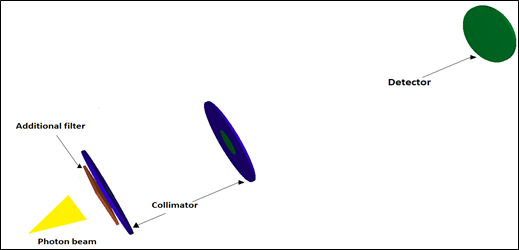
Figure 2 Modeled array used in stage 2 of the simulations. Lead collimator at 30 cm from the source, radius of 1.5 cm and thickness of 5 mm, and another lead collimator at 50 cm from the source, radius of 2.5 cm and thickness of 4 mm, and air detector at 1 m. The photon beam is illustrative only.

Experimental measures

The calibrated ionization chamber model NE 2571 and the electrometer model Keithley 6517ª at the Instituto de Radioproteção e Dosimetria (IRD) were used to measure the charge readings to calculate the HVLs (Figure 3). The ionization chamber was placed one meter away from the source so that, the projection was a circular beam of 10 cm diameter. Two collimator and filters with 99.99% purity before the ionization chamber completed the arrangement.

Figure 3 Setup for the first and second HVLs: a) ionization chamber and b) collimator.

For each filter thickness, five measurements were collected in the ionization chamber and temperature and pressure corrections were applied. Charge readings relative to the value without additional filter were plotted against the different copper thicknesses to calculate the HVLs. Results are shown in Tables 3 and 4.

Determination of mean energy values, half-value layer (HVLs), associated uncertainties and statistical tests.

Formally, the kerma calculation is defined through an integral,²² however, it can be discretized into “n” segments or small bins and a good approximation of this value can be obtained,²³ as determined by equation 1:

$K_i^{air}={\displaystyle \sum _{i=1}^n{K}_i^{air}}={\displaystyle \sum _{i=1}^n{\varphi }_i{E}_i}{\left(\frac{{\mu }_{en}}{\rho }\right)}_i^{air}$    (1)

Where $K_i^{air},E_i,{\varphi }_i$  e ${\left(\frac{{\mu }_{en}}{\rho }\right)}_i^{air}$ are the kerma, photon energy, fluence, and mass energy-absorption coefficient in air corresponding to the i_th bin of the spectrum, respectively. In this way, since the HVL is the thickness necessary to obtain half the intensity of the incident beam when passing through a specific material, and the intensity being proportional to kerma, this can be expressed as follows:

$\frac{1}{2}{\displaystyle \sum _{i=1}^n{K}_i^{air}}={\displaystyle \sum _{i=1}^n{K}_i^{air}\times \exp (-{\mu }_{i}HVL)}$    (2)

The previous expression was used as an equation, so five thickness values of the absorbent material close to the HVL reported by the BIPM were sampled,²⁴ and a straight line was generated through linear regression with these points. From this, the thickness value that satisfied expression 2 could be estimated. The attenuation coefficients of air and copper were taken from the website of the National Institute of Standards and Technology (NIST).²⁵ It’s worth mentioning that equation 2 is strictly applicable only for a narrow beam geometry but was used for our broad beam results as the only way to estimate the HVL.

The mean energy was calculated by multiplying the normalized frequency of x-ray times the corresponding energy value (Y-axis from spectra figures), using equation 3. Mean energy values were compared with those found by the Laboratoire National Henri Becquerel (LNE-LNHB).²⁶

$\overline{E}={\displaystyle \sum _{i=1}^n{f}_i{E}_i}$    (3)

In the calculation of uncertainties, for the case of the simulated spectrum, equation 4 was used, and for the HVL calculation, the values of the standard deviations of 5 charge readings as uncertainty type A and those of type B related to the equipment were determined.²⁷

$u_{HVL}=\frac{dHVL}{dE}{u}_E$    (4)

The overall uncertainties calculated in this work are reported for a confidence level of 95% with a coverage factor of k = 2.

The t-student test was used to compare the spectra, which quantitatively analyzes whether there are statistically relevant differences between them (two-tailed test). This was performed in the GraphPad Prism software (v. 6). So, if the calculated t value is greater than the critical value (p= 0.05) the null hypothesis which states there is a difference between the samples is rejected for a confidence level of 95%.

All energy spectra obtained with the MC simulations present different peaks that refer to the characteristic x-rays of the different materials involved in both stages, as well as continuous values ​​of energy product of the Bremsstrahlung interaction with the tungsten target, as found in previous studies.²⁸ The standard deviation of each energy bin is less than 1% in all simulations. The different spectra are shown in Figures 4-7 and compared with the spectra obtained from the SpekCalc software with the same energy resolution. In stage 1, there were peaks at 8.5, 9.5 and 10 keV from the characteristic x-rays of tungsten L-shell transitions: 8.39, 9.67 and 9.96 keV, respectively. The K-shell transitions are the ones with the highest energy values at 58, 59.5 and 67 keV, corresponding to the theoretical values ​​of 57.98, 59.31 and 67.24 keV. In the case of the SpekCalc spectra, only the peaks of the K-shell transitions are found, since one of the software's limitations is that the L-shell transitions are not modelled, being the lower spectrum limit as 10% of the tube voltage value. In this way, the simulations were divided into two groups, those that had a lower spectrum limit equal to SpekCalc (denoted with *), and those that had a lower spectrum limit with an uncertainty lower than 1%, that is, initial values ​​of 6.0, 6.5, 7.0 and 7.5 keV corresponding to the energies of 100, 135, 180 and 250 kVp, respectively. Note that there is a systematic difference in peak intensities in the first stage, increasing as the tube voltage increases (Table 3). This difference has a great influence on normalization, since when considering low energies in the spectrum with energy intensity peaks like 60 keV, the total sum of intensities increases, thus reducing the relative intensity values, being more accentuated for the discrete energies (peaks) in the spectrum.

Figure 4 X-ray spectra for 100 kVp at the exit of the beryllium window.

Figure 5 X-ray spectra for 135 kVp at the exit of the beryllium window.

Figure 6 X-ray spectra for 180 kVp at the exit of the beryllium window.

Figure 7 X-ray spectra for 250 kVp at the exit of the beryllium window.

In the second stage, a quantitative evaluation was made between the results obtained through the MC simulations and the SpekCalc values. The spectra obtained in this stage are shown in Figures 8-11. Normality tests for the MC results were not performed prior to the statistical tests since the behavior of the data for many particles guarantees that the results are represented by a normal distribution.²⁹ The paired t-student test was chosen, using the difference between the intensities of corresponding bin pairs. The p-values obtained from the test were in the range of 0.77 to 0.90, with no statistically significant differences between the spectra.

Figure 8 X-ray spectra for 100 kVp at 1m from the beryllium window.

Figure 9 X-ray spectra for 135 kVp at 1m from the beryllium window.

Figure 10 X-ray spectra for 180 kVp at 1m from the beryllium window.

Figure 11 X-ray spectra for250 kVp at 1m from the beryllium window.

In addition to the particles interacting with the additional filtrations, there are interactions with the lead collimators, which is evidenced in the peaks at 73, 75 and 85 keV, corresponding to the emission lines of the K-shell with values of 72.80, 74.97 and 84.94 keV, although they have much smaller amplitudes compared to tungsten.

Differences in peaks decreased between MC simulations and SpekCalc results, shown in Table 4, but still with differences. There were also slight differences in the continuous part of the spectra, which is expected since in the MC simulations the beam is approximated as close to reality as possible, to give a broad beam (also known as wide beam), so that the contribution of scattered radiation is included in the measurement. Moreover, additional filters reduced the low energies, but peaks in the range of 8 to 10 keV were still found, although they are not perceptible in Figures 8-11.

The systematic difference still prevails in the amplitudes of the peaks of the second stage in relation to the SpekCalc data. This behavior is found in other studies with a similar energy range³⁰ where the energy peaks for values above 100 kV simulated with MC are superior to those of SpekCalc. This difference would have an important contribution to the difference in HVL values compared to the software, since in the HVL calculation these intensities are proportional to kerma (equation 1). Equation 2 was used to calculate the HVLs from the MC simulation, SpekCalc values and the readings from experimental measurements, presented in Tables 5 and 6. The results given in Table 9 were obtained from equation 3.

In summary, the differences in the peaks, the low energy region where there is still contribution of the peaks smaller than 10 keV as well as the difference in the scattering of the broad beam, in relation to the beam with good geometry modeled in SpekCalc, have a final impact on the calculation of the first and second HVL for each quality (Tables 5 and 6). Disregarding intensities lower than 10 keV, differences of less than 3% were obtained in relation to SpekCalc for the 3 highest energies in terms of the values of the first HVLs (Table 7). In the case of the second HVLs, the impact of this range below 10 keV had the same behavior as that of the first HVLs, since the equation for calculating this other parameter follows equation 2, changing only the factor two for four in the denominator on the left side.

Regarding the measurements used to calculate the HVLs of the second tube (with maximum peak kilovoltage of 250 kVp), there were relevant differences of less than 20% in relation to the simulations, with these being reduced to around 10% or less for the reduced spectrum (Table 8). However, there are studies where the HVL values were calculated by different laboratories²⁶ and differences between 5 and 10% were reported, even with additional filters of similar values. There is still no consensus on the tolerance value of the HVL for qualities in this energy range.

The differences between the mean energy values did not have the same order of discrepancy as those of the HVL, shown in Table 9, where differences of less than 2.5% were obtained. (Tables 10&11)

As expected, those photons that interact along their path with the different materials involved for each one of those qualities, produce secondary electrons. These were recorded in the same detector as the primary particles, and their spectra are shown in Figures 12-15, and the corresponding mean energy values are given in Table 12. Thus, in the second stage, the number of simulated histories was required to be much higher compared to stage 1 to acquire a result with an uncertainty of less than 2% for each energy bin of the electron spectrum.

Figure 12 Spectra of secondary electrons at 1m from the 100 kVp beam quality.

Figure 13 Spectra of secondary electrons at 1m from the 135 kVp beam quality.

Figure 14 Spectra of secondary electrons at 1m from the 180 kVp beam quality.

Figure 15 Spectra of secondary electrons at 1m from the 250 kVp beam quality.

The beam qualities with maximum nominal energies of 100, 135, 180 and 250 kVp were studied in detail, with differences for two different simulation scenarios identified in relation to HVL values reported in the literature. However, the t-student statistical test applied between the spectra for each quality did not show statistically relevant differences, as the study reported by Ay et al.³⁰ In the case of mean energies, similar values were found with other works, without a significant impact on HVL values for these energies.

The computational requirement involved in the present study was high complex to produce more accurate results with low uncertainty, especially in the second stage, which required variance reduction techniques and parallel simulations. Interesting to observe the difference between the SpekCalc data obtained for narrow beam geometry with the data generated by Monte Carlo for broad beam geometry.

The results of the energy spectra of the secondary electrons obtained in the second stage of the simulations is a new contribution to the area of medical physics, since the related studies neglect these particles, focusing exclusively on the primary particles and their interactions with the different materials of the simulations.

Since electrons are directly ionizing particles, they deliver their energy locally to the medium, and their characterization is of vital dosimetric importance. In fact, future works should consider the contribution of these particles to obtain more accurate results, especially those that support direct interactions with the media. This is the case for instance of the Fricke dosimetry since the chemical reaction are provoked by the electron and the mean energy of the electrons may become a parameter of normalization and not the mean energy of the photons.

We thank the technical staff of the Instituto de Radioproteção e Dosimetria – IRD for carrying out the measurements of the first and second HVL. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001.

None.

1. Khoshgard K, Hashemi B, Arbabi A, et al. Radiosensitization effect of folate–conjugated gold nanoparticles on HeLa cancer cells under orthovoltage superficial radiotherapy techniques. Phys Med Bio. 2014;59(9):2249–2263.
2. Cheraghi N, Cognetta JrA, Goldberg D. Radiation therapy for the adjunctive treatment of surgically excised keloids: a review. The J Clin Aesthet Dermatol. 2017;10(8):12–15.
3. Wanbao G, David E. Orthovoltage radiation therapy treatment planning using Monte Carlo simulation: treatment of neuroendocrine carcinoma of the maxillary sinus. Phys Med Biol. 1997;42(12):2421–2433.
4. Pampena R, Palmieri T, Kyrgidis A, et al. Orthovoltage radiotherapy for nonmelanoma skin cancer (NMSC): Comparison between 2 different schedules. J Am Accad Dermatol. 2016;74(2):341–347.
5. Laitiano RF, Pani R, Pellegrini R. Determination of x–ray spectra and of the scattered component up to 300 kV. Med Phys. 1991;18(5):934–938.
6. Antonuk LE, El–Mohri Y, Siewerdsen JH, et al. Empirical investigation of the signal performance of a high–resolution, indirect detection, active matrix flat–panel imager (AMFPI) for fluoroscopic and radiographic operation. Med Phys. 1997;24(1):51–70.
7. Wilkinson E, Johnston PN, Heggie JC. A comparison of mammography spectral measurements with spectra produced using several different mathematical models. Phys Med Biol. 2001;46(5):1575–1589.
8. Fewell, TR, Shuping RE. Photon energy distribution of some typical diagnostic x–ray beams. Med Phys. 1997;4(3):187–197.
9. Fewell TR, Shuping RE, Healy KE. Handbook of computed tomography x–ray spectra (HHS Publication) (FDA) 81–8162 (Washington, DC: US Govt. Printing Office), 1981.
10. Boone JM, Fewell TR, Jennings RJ. Molybdenum, rhodium, and tungsten anode spectral models using interpolating polynomials with application to mammography. Med Phys. 1997;24(12):1863–1874.
11. Blough MM, Waggener RG, Payne WH, et al. Calculated mammographic spectra confirmed with attenuation curves for molybdenum, rhodium, and tungsten targets. Med Phys. 1998;25(9):1605–1612.
12. Omrane LB, Verhaegen F, Chahed N, et al. An investigation of entrance surface dose calculations for diagnostic radiology using Monte Carlo simulations and radiotherapy dosimetry formalisms. Phys Med Biol. 2003;48(12):1809–1824.
13. Aguirre E, De Almeida, CE, David M, et al. Estudo da distribuição de dose de feixes clínicos de elétrons em meios heterogêneos. Brazilian Journal of Radiation Sciences. 2020;8(3).
14. Aguirre E, De Almeida C. Estudo de espectros em feixes de raios–x de energia média em radioterapia utilizando o método Monte Carlo através de dosimetria Fricke. Tese de doutorado. Universidade do Estado do Rio de Janeiro, 2022.
15. Rogers D. Fifty years of Monte Carlo simulations for medical physics. Phys Med Biol. 2006;51(13):R287–R301.
16. Bielajew AF. Fundamental of the Monte Carlo method for neutral and charged particle transport. 1. ed. The University of Michigan: [s.n.], 2011.
17. Poludniowski G, Landry G, Deblois F, et al. SpekCalc: a program to calculate photon spectra from tungsten anode x–ray tubes. Phys Med Biol. 2009;54(19):N433–N438.
18. Salvat F, Fernandez–Varea JM, Sempau J. PENELOPE: A code system for monte carlo simulation of electron and photon transport. Issy–Les–Moulineaux, France. 2018.
19. X–ray tube manufacturer specifications.  
20. Badal A, Sempau JA. Package of Linux scripts for the parallelization of Monte Carlo simulations. Comput Phys Comn. 2006;175:440–450.
21. Rosado PH, Salata C, David MG, et al. Determination of the absorbed dose to water for medium–energy x–ray beams using Fricke dosimetry. Med Phys. 2020;47(11):5802–5809.
22. Attix FH. Introduction to radiological physics and radiation dosimetry. 1. ed. Germany: John Wiley & Sons, 2008.
23. LB Rall. Numerical integration and the solution of integral equations by the use of riemann sums, SIAM. J Numer Anal. 1965;7:55–64.
24. Kessler C, Burns D, Büermann L. Key comparison BIPM.RI(I)–K3 of the air–kerma standards of the PTB, Germany and the BIPM in medium–energy x–rays. Metrologia. 2011;48(1A):06011.
25. Hubbell J, Seltzer S. Table of X–ray mass attenuation coefficients and energy absorption coefficients. National Institute of Standards and Technology (NIST) webpages. 2010.
26. Bjerke H, Plagnard J, Bordy J–M, et al. Comparison of the air–kerma standards of the NRPA, the STUK, the SSM and the LNE–LNHB in medium–energy x–rays (EURAMET.RI(I)–S15). Metrologia. 2018;55:06007–06007.
27. David MG, Pires EJ, Bernal MA, et al. Experimental and Monte Carlo–simulated spectra of standard mammography–quality beams. Br J Radiol. 2012;85(1013):629–635.
28. Bhat M, Pattison J, Bibbo G, et al. Diagnostic x–ray spectra: a comparison of spectra generated by different computational methods with a measured spectrum. Med Phys. 1998;25(1):114–120.
29. JAMES F. Monte Carlo theory and practice. Reports on progress in Physics. IOP Publishing. 1980;43(9):1145.
30. Ay MR, Shahriari M, Sarkar S, et al. Monte Carlo simulation of x–ray spectra in diagnostic radiology and mammography using MCNP4C. Phys Med Biol. 2004;49(21):4897–4917.