The concern about the climate issue has been increasing since climate change influence the water resources system. For this reason, this study sought to identify the presence of trends in the historic series of two meteorological variables: total annual precipitation and number of rain days, in the state of Bahia, Brazil, in order to verify if the precipitation regime is being affected by the global climate change. Two trend tests were applied: Mann-Kendall and Linear Regression, with significance levels of 5% and 10%, in the historical series of 32pluviometric stations distributed throughout the state. The results of the two testes were similar, which guarantees that both can be used for detection of changes in rain pattern. The study confirms that in a specific region of Bahia, more specifically in the central and eastern areas, there is a reduction trend in the historical series of annual precipitation. Regarding the number of rain days, no trend conclusions were observed. 

Keywords: meteorological variables, trend, climate change, mann-kendall, linear regression

ANA, national water agency of brazil; BDMEP, meteorological database for education and research; HidroWeb, hydrological information system; INEMA, environmental and water resources institute of the state of bahia; INMET, national institute of meteorology of brazil; IPCC, intergovernmental panel on climate change; ITCZ, intertropical convergence zone; LR, linear regression; MK, mann-kendall; N, number of rain days; P, total annual precipitation; SACZ, south atlantic convergence zone; SEIA, state system of environmental information and water resources.

The state of Bahia is located on the Northeast region of Brazil and occupies an area of 564.733,177km². According to the Brazilian Institute of Geography and Statistics, it is divided in 417cities.¹ The state has a unique topography, composed by flat lands, highlands, valleys and ridges; a peculiar vegetation, that ranges from dense forests (Atlantic Rainforest) to xerophytic vegetation in the Caatinga area on the north central region of the state. It is subjected to various meteorological systems that contribute to define its pluviometric regime, such as: Intertropical Convergence Zone (ITCZ), Frontal Systems, South Atlantic Convergence Zone (SACZ), tropical waves, sea and land breeze and mountain and valley breeze. The combination of these heterogeneous characteristics produces a spatial variability of precipitation throughout the state with respect to the total precipitation volume and the rain distribution during the year.²

This heterogeneity raises the need for analysis of the pluviometric regime behavior in view of the variations caused by potential effects of climate change. According to results published in IPCC reports (Intergovernmental Panel on Climate Change), pluviometric regimes of some regions of the world are being altered, increasing the frequency of extreme events (intense rains and long droughts).³ 

The climate variability and changes influence directly human activities and natural systems biodiversity. When the temperature and dynamic of water resources are modified, several economic sectors are affected, especially those dependent of environmental systems, such as agriculture, which is scheduled using the hypothesis that rains are homogeneous series. Mortatti et al.⁴ and Naghettini and Pinto⁵ outline the significance of verifying the non stationarity of hydrological series once they provide the theoretical basis for rational usage, water conservation and energy planning.

Such verifications are being carried out for some time in international context, for instance in Asia,^6,7 Africa,⁸ Oceania,⁹ Europe¹⁰and North America.¹¹ In Brazil, there are studies that investigate these trends. Alexandre, Baptista and Naghettini¹² performed a trend analysis in Belo Horizonte Metropolitan Region (state of Minas Gerais). Their results pointed out no significant data trend.

Scofield, Angelis and Sousa Junior¹³ studied the trend in the historic series of rain indicators (number of rain days, smaller and greater precipitation rate and total precipitation) on the Northeast coast of São Paulo state. There was no significant change in total precipitation during summer, however all other seasons showed upward trend for this index. Concerning rain days, in autumn and summer was verified upward trend, while in winter and spring, the trend was downward.

Rosin, Amorim and Morais¹⁴ developed a research to evaluate the trend in the historic series of precipitation and flow rate of the Rio das Mortes basin (state of Mato Grosso). The analysis presented inconclusive results once they identified as much positive as negative trends.

A more recent study was conducted on the São Francisco river basin by Silveira et al.¹⁵ This research aimed to analyze variations in the historic series of precipitation and temperature on this region. Results pointed to an upward trend of temperature for the whole area in study, however, with respect to precipitation, some locations showed increasing and other decreasing trends.

Silva et al.¹⁶ identified climate variation in the region of transition between the Amazonian vegetation and Savannah on the state of Maranhao, in which stations of different biomes indicated precipitation trends for distinct seasons, with precipitation increase in the rainy season and reduction during drought. This suggests impacts in the whole dynamic of the physical environment.   

Observing the amount of studies, one can perceive the relevance given to this topic by researchers. With respect to the state of Bahia, target of this work, few studies were made to detect variation in its pluviometric regime.

Lima et al.¹⁷analyzed historical series of precipitation and temperature of 16 stations in the time period from 1961 to 2009. Only two pluviometric stations presented significant trend with respect to total annual precipitation: Caravelas (increase) and Cipó (decrease). As for temperature, except for the station of Canavieiras, all showed significant upward trend.

Araujo and Brito¹⁸ studied 75pluviometric stations in order to identify climate variations in the states of Bahia and Sergipe. Climate indexes were calculated using the temporal series from 1947 to 1991 to verify the presence of a trend. It was concluded that with respect to total precipitation, there was an upward trend for the stations, specially for those located on the extreme west and northeast of the state and a downward trend in the São Francisco river valley and on the south of the state.

Silva, Souza and Azevedo¹⁹studied the behavior of 8stations spread along the state of Bahia using the historic series from 1970 to 2006. The obtained results showed that Chapada Diamantina, west and southwest regions had reduction trends in precipitation. For the mesoregion of Lower Middle São Francisco river, two stations presented reduction trend (Barra e Bom Jesus da Lapa), while one station (Carinhanha) presented increasing trend.

Tanajura, Genz and Araujo²⁰ developed a study applying data from 29pluviometric stations in the state of Bahia, with historic series from 1960 to 1990. The applied method was based on the weather simulation of the state as it presents itself currently and its possible changes in the years 2070 to 2100. Therefore, the regional atmospheric model HadRM3P coupled to the global model HadAM3 was used. Sceneries A2 and B2 from IPCC were reproduced in order to perform this prediction. The first one presents a pessimistic scenery, considering that society will not be concerned about climate change in the future. The second scenery presents the opposite situation. A possible decrease in precipitation was detected for the whole state.

Reasoning from this background, observing the low quantity of works about the state of Bahia, with limited scope and low number of stations and considering the relevance of the historic precipitation series behavior to the management of water resources, specially in agriculture and rainwater harvesting, this study sought to evaluate the precipitation behavior trend in the state of Bahia. It must be highlighted that this work did not aim to identify the physical causes of these trends, if observed, but to investigate its occurrence.

In this study, daily, monthly and annual precipitation series from 32pluviometric stations spread throughout the state of Bahia with historic series of 52years [1966–2017] of data were used. The names of these stations as well as its locations are showed on Table 1 and Figure 1, respectively. There is a good distribution of the pluviometric stations, which makes possible a better representation of the state's situation.

Figure 1 Spatial distribution of 180 pluviometric station in the state of Bahia.

The data used in this study was obtained in the SEIA (State System of Environmental Information and Water Resources) database of the Environmental and Water Resources Institute of the state of Bahia (INEMA); HidroWeb (Hydrological Information System) platform created by the National Water Agency of Brazil (ANA); and BDMEP (Meteorological Database for Education and Research) of the National Institute of Meteorology of Brazil (INMET).

 A data investigation was performed and eventual gaps in series were filled. Subsequently, a consistency analysis was applied using interpolation methods^21,22 in order to verify the homogeneity of the results.

Statistical tests

Two meteorological variables were chosen to be evaluated with respect to the occurrence of trends in their historical series: annual total precipitation (P) and the number of rain days (N), which corresponds to the sum of days with precipitation above 1mm as described by Araújo and Brito¹¹ and Farias, Alves and Nobrega.²³ Therefore, two statistical methods were used to evaluate the trend of these two meteorological parameters: Regression Analysis and Mann-Kendall tests, considered the most commonly used to identify possible changes in the pluviometric regime of a region from its historic series.

Mann-kendall test

Two hypothesis are tested in this method. Firstly, the null hypothesis , which occurs when the data are independent and identically distributed. Secondly, the hypothesis  is tested, which occurs when there is a trend in the historic series. The test consists in comparing each value of a series with the previous in a sequential form. Then, the quantity of times that this number was greater, smaller and equal to zero is counted. Hence, the statistical test (S) is defined by Equation 01.^24,25

$S= {\displaystyle \sum }_{k=1}^{n-1}{\displaystyle \sum }_{k+1}^{n}sign\left(x_j-x_k\right)$      (01)

Where n is the length of the series; k = 1, 2,…, n-1; j = 2, 3, …, n and  is the sign function, defined as:

sign (x) = $\{\begin{array}{c} 1, if x>0 \\ 0, if x=0\\ -1, if x<0\end{array}$   (02)

 The statistical test S tends to a normal distribution, with null mean and variance Var(S). This value is given by:

$Var \left(S\right)= \frac{\left[n.\left(n-1\right).\left(2.n+5\right)\right]}{18}$      (03)

It must be noted that even for small values of n, the statistical S can be treated as a normal distribution. Therefore, the method^24,25,26 can be applied. The test is applicable even for series with only 15items, as the used part of the sample.

Once the variance is defined, the statistical pattern, Z, is calculated.

$Z= \{\begin{array}{c}\frac{S-1}{\sqrt{Var \left(S\right)}}, S>0\\ 0, S=0\\ \frac{S+1}{\sqrt{Var \left( S\right)}}, S<0\end{array}$      (04)

In order to verify the upward or downward trend to the significance level of p, the null hypothesis is rejected if the absolute value of Z is greater than a chosen value, using the normal distribution table.^17,27,28 In the present research, the adopted significance level was 5% and 10%, Hence, according to the normal distribution table, the trend is significant at 5% if Z<-1,96 to a negative trend and Z>1,96 to a positive trend. Meanwhile, the trend is significant at 10% if Z<-1,65 to a negative trend and Z>1,65 to a positive trend.

Although increasing the statistical error with the value of 10%, this level of significance is appropriated since the rain phenomenon is random e highly complex, not affecting the reliability of the results. This research used a conservative criteria, which considers that the station that did not present significant trends for the significance level of 10% do not have trends.

Regression analysis

Regression is characterized as a parametric test that relates two or more variables aiming to verify the degree of influence that one variable suffers with respect to other(s). According to Penereiro and Ferreira,²⁹ regression analysis is relevant to identify time-series behavior with the focus of having an initial concept about the behavior of the possible trend.

In this research, simple linear regression (LR) was used, which assumes that the relationship between the two studied variables is a line. The test was applied with the option of adjusting the trend line for the levels of significance of 5% and 10%.

To define the result of this method, the gradient of the function is evaluated. Positive values indicate upward trend and negative values represent downward trend. Considering linear regression, the trend is significant at a significance level is the value of p is smaller that the adopted significance.

Table 2 presents the number of stations that showed significant trend for each method. The detailed description of these results for each rain indicator is listed on the following table. 

Total annual precipitation (P)

For the total annual precipitation parameter, according to the MK test, it was concluded that only 13stations showed significant trend for the significance level of 5%, one upward and the others downward. That corresponds to approximately 41% of the total pluviometric stations. For the linear regression test, the same result was achieved, as can be seen on Table 3.

Considering that the rain phenomenon is random, specially due to its dispersion, statistical tests were applied again, but with the significance level increased to 10%. It was verified that only three more pluviometric stations showed an annual precipitation trend. Two of those were obtained using the linear regression test: Andaraí (1), that showed downward trend with gradient equal to -5,31 and p-value of 0,10, and Brotas de Macaúbas (5), that presented upward trend with gradient equal to 3,74 and p-value of 0.09. The third city was Caetité, that presented negative trend on Mann-Kendall test, with Z=-1,91.

As can be perceived, the increase of the significance level of Mann-Kendall and linear regression tests for annual precipitation did not result in a significant rise in the number of cities with trends. Figures 2&3 show the distribution of stations and its corresponding trends according to Mann-Kendall and Linear Regression tests, respectively.

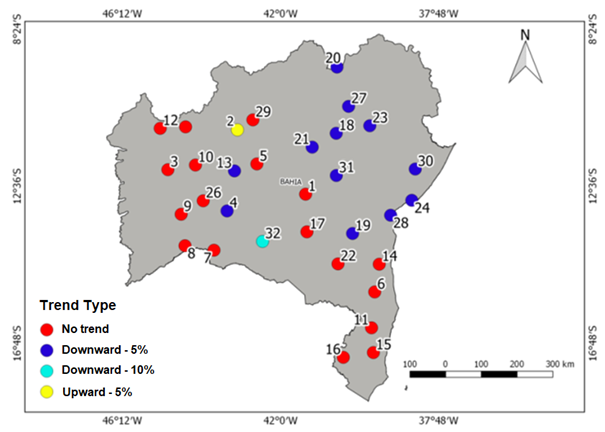
Figure 2 Spatial distribution of pluviometric stations with respect to Total Annual Precipitation trend, using Mann-Kendall test.

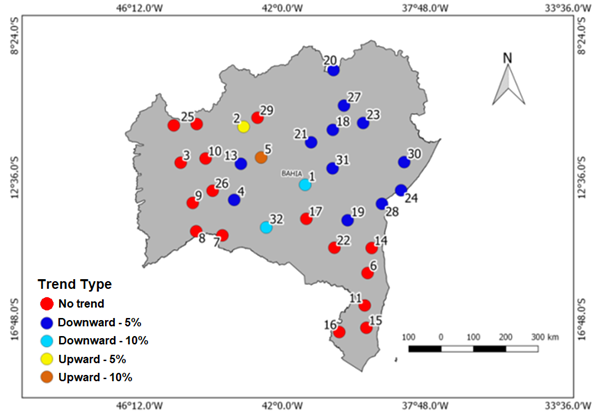
Figure 3 Spatial distribution of pluviometric stations with respect to Total Annual Precipitation trend, using Linear Regression test.

The analysis of maps allows one to deduce that, generally, no alteration in total annual precipitation can be detected on the entire state. However, it was possible to verify these trends in some areas, such as Central mesoregion (represented by Chapada Diamantina), Reconcavo Baiano (near the coastline), Northeast, North and Southwest, which presented a reduction trend in precipitation for both methods. Those areas concentrate pluviometric stations 21, 18, 23, 27, 30, 31, 28, 24, 19 and 20 as showed by the maps in Figures 2&3.

Additionally, one can observe the significant reduction of the rain indicator in the coast region of the state, represented by the city of Salvador, similar to the result obtained by Tanajura, Genz and Araujo.²⁰ These authors observed a decrease in precipitation up to 70% on the coastline. It is noteworthy that in this area are the two largest cities in the state, Salvador and Feira de Santana, which inhabit about 5million inhabitants. In addition, this region includes important water sources and is also home to the two largest industrial centers in the state: Camaçari Petrochemical Complex and Aratu Industrial Center, the latter being an important irrigation area.

The change in the rainfall regime brings considerable economic impacts to society, since large sectors that depend on the rain seasonality, such as agriculture, are influenced by the change in this regime. This results in a scarcity of resources and the need to invest in different forms of production. From an environmental point of view, ecosystems are modified by altering the natural habitat, which influences the survival of living beings.

Lima et al.¹⁷ also applied the MK trend test in their research, although using only 16stations spread throughout the state of Bahia. Six of these stations were contemplated again in the present work (Barreiras, Bom Jesus da Lapa, Carinhanha, Jacobina, Morro do Chapéu and Salvador). Table 4 presents the comparison between the results of both studies.

Lima et al.¹⁷ used a historic precipitation series between the years 1961 and 2009, and the present study used a more recent series in the analysis, ranging from 1966 to 2017. Based on Table 4, one can observe that the 8 years of more recent information altered the results with respect to the trend of four pluviometric stations. Bom Jesus da Lapa, Jacobina, Morro do Chapéu and Salvador had not shown significant trend in the previous study, while the present work detected precipitation reduction in these locations. Possibly, this change in the water regime was detected due to the occurrence of severe drought during the period from 2009 to 2016.

Number of rain days (N)

According to Mann-Kendall test, with significance level of 5%, 15cities presented trends concerning the number of rain days, being 5 upward and 10 downward trends, representing approximately 47% of the analyzed sample. Using the Linear Regression test, 13cities showed trends with a 5% significance level, being 5 upward and 8 downward, which represents approximately 41% of all the studied pluviometric stations. Table 5 shows which stations had significant trends and its respective values.

Considering the increase of the significance level to 10%, it was verified that only one more pluviometric station (Barra) presented significant trend. This was identified using the Linear Regression test as an upward trend with gradient equal to 0,20 and p-value equal to 0,07. From an analysis of results with respect to the significant trend detected by the two methods, it was observed that 7pluviometric stations (Alagoinhas, Bom Jesus da Lapa, Ibotirama, Jacobina, Jequié, Salvador and Senhor do Bonfim) presented reduction in both number of rain days and total annual precipitation when applying the Mann-Kendall tests and 5pluviometric stations (Alagoinhas, Bom Jesus da Lapa, Jacobina, Jequié and Senhor do Bonfim) showed reductions in the two parameters when using Linear Regression. These results suggest that besides the reduction in the pluviometric index, the cities are also likely to have a greater drought.

Additionally, it can also be observed the data generated by each method have a good agreement spatially with respect to the kind of trend  detected in each region of the state, as demonstrated in Figures 2&3, and individually for each station. A small number of incompatibilities was verified as, in some cases, one method resulted in significant trend for one parameter and the other method did not have the same correspondence. When analyzing the value of Z and the parameters obtained with the linear regression for these stations, the trend in question was confirmed since the difference between test results is explained by the sensibility of these methods. The values of Z and p to these stations were close to the limit for trend detection at significance levels of 5% and 10%.

The comparison performed above confirms that even with the limitations of the Linear Regression test to detect trends in historic time-series, due to the great dispersion in rain data, it generated similar numbers to the ones obtained with Mann-Kendall, which is known in the scientific community as a more reliable method. For this reason, LR can be useful on trend detection for rain indicators.

Finally, observing the results, is not possible to claim a change in rain behavior for the whole state of Bahia, since a limited number of stations presented trends for the two analyzed rain indicators. A local variation in rain regime can be acknowledged.

The present study applied Mann-Kendall and Linear Regression trend tests in the historic series of two meteorological variables: total annual precipitation and number of rain days, in order to identify changes in the water regime in the state of Bahia, Brazil. Both tests presented similar results, which suggests that both may be implemented to detect alterations in rain behavior. This article becomes relevant due to the great extent of the state and its strong influence on the economic sector in Brazil. In this sense, the state is greater in large European countries such as Germany, Spain, France and Portugal or which ratifies an importance of this research. There is no common trend for the entire state, although it may indicate a specific region in Bahia, like the central and eastern areas, there is a reduction trend in the annual historical series. It is noteworthy that in this region, it locates the two biggest cities in the state, Salvador and Feira de Santana, which shows the importance of these results. With respect to the other analyzed indicator, number of rain days, no region showed significant trend. Therefore, no conclusions were obtained about this parameter. This situation already represents a warning, since it signals to an alteration in the water regime of the state. The causes of the identified trends for the state and for its mesoregions are not included in the scope of this research. Hence, the answer to these questions is suggested as a purpose for future works.

None.

The authors declare that there is no conflict of interest.

None.

1. IBGE. Instituto Brasileiro de Geografia e Estatística. Bahia. IBGE; 2014.
2. Braga CC, Melo MLD, Melo ECS. Cluster Analysis Applied to Precipitation Distribution in the State of Bahia. Proceedings of the 10thCongresso Brasileiro de Meteorologia; 1998; Brasília‒DF: Sociedade Brasileira de Meteorologia; 1998. p.1857‒1862.
3. IPCC. Intergovernmental Panel on Climate Change. Climate change and land: an IPCC Special Report on climate change, desertification, land degradation, sustainable land management, food security, and greenhouse gas fluxes in terrestrial ecosystems. Summary for Policymakers. IPCC; 2019.
4. Mortatti J. Hydrology of the Tietê and Piracicaba rivers: time series of flow and flood hydrographs. Revista de Ciência & Tecnologia. 2004;12(23):55‒67.
5. Naghettini M, Pinto EJA. Hidrologia estatística. Belo Horizonte: CPRM; 2007. 552. p.
6. Latif M, Syed FS, Hannachi A. Rainfall trends in the South Asian summer monsoon and its related large‒scale dynamics with focus over Pakistan. Climate Dynamics. 2017;48(11‒12):3565‒3581.
7. Partal T. Multi‒annual analysis and trends of the temperatures and precipitations in West Anatolia. Journal of Water and Climate Change. 2017;8(3):456‒473.
8. Onyutha C. Analyses of rainfall trends in the Nile River Basin. Journal of hydro‒environment research. 2016;13:36‒51.
9. Davis CJ, Hanna EG. Temperature and rainfall trends in northern Australia 1911‒2013: implications for human activity and regional development. Climate Research. 2016;71(1):1‒16.
10. Baiamonte G, D’Asaro F. Discussion of “Analysis of Extreme Rainfall Trends in Sicily for the Evaluation of Depth‒Duration‒Frequency Curves in Climate Change Scenarios” by Lorena Liuzzo and Gabriele Freni. Journal of Hydrologic Engineering. 2016;21(6): 07016005.
11. Rahmani V. Analysis of frequency and magnitude of extreme rainfall events with potential impacts on flooding: a case study from the central United States. International Journal of Climatology. 2016;36(10):3578‒3587.
12. Alexandre GR, Baptista MB, Naghettini M. Study to Identify Trends in the Rainfall Regime in the Metropolitan Region of Belo Horizonte from Statistical Methods. Revista Brasileira de Recursos Hídricos. 2010;15(2):115‒126.
13. Scofield GB, Angelis CF, Sousa Junior WC. Study of trends in total precipitation and number of rainy days on the north coast of São Paulo. Revista Brasileira de Recursos Hídricos. 2014;19(3):19‒31.
14. Rosin C, Amorim RSS, Morais TST. Analysis of hydrological trends in the Rio das Mortes basin. Revista Brasileira de Recursos Hídricos.  2015;20(4):991‒998.
15. Silveira CS. Climate change in the São Francisco River basin: An analysis for precipitation and temperature. Revista Brasileira de Recursos Hídricos. 2916;21(2):416‒428.
16. Silva FB. Evidence of climate change in the Amazon‒Cerrado transition region in the state of Maranhão. Revista Brasileira de Meteorologia. 2016;31(3):330‒336.
17. Lima JRA, et al. Identification of climate trends in the State of Bahia. Revista de Geografia. 2011;28(3):172‒187.
18. Araujo WS, Brito JIB. Climate change trend indices for the states of Bahia and Sergipe using daily rainfall indices and their relationship with Pacific and Atlantic TSM. Revista Brasileira de Meteorologia. 2011;26(4):541‒554.
19. Silva GB, Souza WM, Azevedo PV. Scenarios of Climate Change in the State of Bahia through Numerical and Statistical Studies. Revista Brasileira de Geografia Física. 2012;05(05):1019‒1034.
20. Tanajura CAS, Genz F, Araújo HA. Climate change and water resources in Bahia: validation of the current climate simulation of HADRM3P and comparison with scenarios A2 and B2 for 2070‒2100. Revista Brasileira de Meteorologia. 2010;25(3):345‒358.
21. Paulhus JLH, Kohler MA. Interpolation of missing precipitation records. Monthly Weather Review. 1952;80(8):129‒133.
22. Bertoni JC, Tucci CEM. Precipitação. In: Tucci CEM, Editor. Hidrologia: Ciência e aplicação. 4th edn. Porto Alegre: ABRH; 2013. p.177‒241.
23. Farias RFL, Alves KMAS, Nóbrega RS. Climatology of occurrence of extreme precipitation events in the mesoregion of the Pernambuco backlands. Revista Geonorte, Special edition 2. 2012;1(5):930‒941.
24. Mann HB. Nonparametric tests against trend. Econometrica: Journal of the Econometric Society. 1945;13(3):245‒259.
25. Kendall MG. Rank correlation methods. 2nd edn. New York: Hafner; 1970.
26. Groppo JD. Estudo de Tendências nas séries temporais de qualidade de água de rios do Estado de São Paulo com diferentes graus de intervenção antrópica. 2005. Dissertation (Master in Ecology of Agroecosystems) ‒ Escola Superior de Agricultura Luiz de Queiroz, Universidade de São Paulo: Piracicaba, 2005. 86 f.
27. XUMEI L, et al. Spatial and temporal variability of precipitation concentration index, concentration degree and concentration period in Xinjiang, China. Inter. Journal of Climatology. 2010;31:1679‒1693.
28. Silva,DF, Sousa AB. Detection of Climate Trends in the State of Alagoas. Revista Brasileira de Geografia Física. 2013; 6(03):442‒455.
29. Penereiro JC, Ferreira DHL. Technology‒backed statistics: a proposal to identify climate trends. Acta Scientiae, Porto Alegre. 2012;13(1):87‒105.