The spatial discretization of a watershed can directly influence the derived outputs of hydrological models? Conclusive guidelines regarding the proper level of spatial discretization have not yet been established due to the great diversity of models, calibrated parameters and topographic and geospatial characteristics of study areas. The objective of this study was to investigate the influence of different levels of watershed spatial discretization (2, 4, 8, 16 and 32 sub basins) on the HEC-HMS model’s performance, considering the Environmental Protection Area (APA) of the Uberaba River Basin region. The SCS-CN method was applied to the different levels of spatial discretization for two distinctive periods (calibration and validation) and its performance was evaluated according to seven goodness-of-fit measures: MAE, RMSE, RSR, NSE, PBIAS, R2 and KGE. The results obtained from a qualitative and quantitative perspective, based on the visual analysis of the simulated hydrographs and the obtained goodness-of-fit values; indicate the HEC-HMS model represents the hydrological processes of the basin under investigation efficiently, regardless of the level of spatial discretization. The results suggest the subdivision of a watershed does not result in improvement of the HEC-HMS model’s performance without significant differences in physiographic characteristics (slope, land use and types of soil). Considering its good performance for the study area, it is suggested the application of the HEC-HMS model for future works that aim to investigate the drainage capacity of the APA of the Uberaba River.

Keywords: catchment size, GIS, soil conservation service, hydrological modelling, spatial discretization,

ANA, brazilian national water agency; BDMEP, meteorological database for education and research; CN, curve number; DEM, digital elevation model; EPA, environmental protection area; GIS, geographic information system; HEC, hydrologic engineering center; HMS, hydrologic modeling system; KGE, kling-gupta efficiency; MAE, mean absolute error; NSE, nash-sutcliffe efficiency; PBIAS, percent bias; R², coefficient of determination; RMSE, root mean squared error; RSR, RMSE-observations standard deviation ratio; SCS, soil conservation service; UH, unit hydrograph; USACE, united states army corps of engineers.

A watershed is a natural catchment area, composed of hill slopes and a drainage network, where the collected rainfall is converted into a single riverbed, whose outlet is known as river mouth. It can be regarded as a system, where the input is the precipitation and the output is the volume of water that leaves the river basin through its mouth, considering as losses the evaporation, transpiration and infiltration.¹ A watershed is the hydrological unit most suitable for studies, since it provides an ideal modeling environment where you have a known input, precipitation data, and a known output, stream gage data.² Hydrological modelling aims to understand and represent the hydrological processes that occur in a watershed, based on the simulation of different scenarios. It can be described as a tool that enables the prediction and estimation of extreme events, as well as to assist in water resource planning and management processes.³

Hydrological simulation depends on how well the watershed processes are represented by the model and on how representative the input parameters values are.⁴ Consequently, it is common practice to discretize the watershed into subbasins, where each subbasin is presumed as a homogeneous spatial unit, in order to better represent its heterogeneities, such as the channel network, the topography, the types of soils, the land use, and the climate inputs.⁵ The spatial discretization of a water catchment directly affects the model outputs, such as peak discharge, outflow hydrograph, time to reach peak discharge, and stream routing.⁶ This is due to the changes in the input parameters, seeing as: the basin’s boundaries predetermines aggregation patterns of spatial information; the topographic parameter values are influenced by the basin’s size and extent; and the characteristics of the drainage network can cause misrepresentation of the rainfall-runoff process.⁷ Guidelines for the most appropriate discretization scheme are often poorly defined and left to the modelers’ discretion.⁸ This can be related to the diversity of existing models, calibrated parameters and topographic and geospatial characteristics of different study areas.⁷ This paper aimed to investigate the influence of different levels of spatial discretization (2, 4, 8, 16 and 32 subbasins) on the HEC-HMS model’s performance, considering the Environmental Protection Area (APA - Área de Proteção Ambiental) of the Uberaba River region as the study area. This region is under intense pressure from urban development companies, which demonstrates the relevance of hydrological studies in the area, since these can help prevent problems like those Uberaba city faces today, such as floods caused by extreme rainfall events.

Study Area

In order to run the HEC-HMS model in the drainage area concerning the Uberaba gaging station (code 61794000) belonging to the Brazilian National Water Agency (Agência Nacional das Águas – ANA), located in the longitude 47°58'42.96''W and latitude 19°43'41.16''S, the study was conducted more precisely in an area that exceeds the legally established territorial boundaries for the Environmental Protection Area (Área de Proteção Ambiental – APA) of the Uberaba River Basin. The APA of the Uberaba River Basin, acknowledged as a Sustainable Land Use Conservation Unit by Brazilian Federal Law n° 9.985/2000, is located on Cerrado Biome, in the city of Uberaba, Triângulo Mineiro Region, State of Minas Gerais, Brazil. This area, located upstream of the city’s water catchment point for public supply, was created with the purpose of guaranteeing the conservation of the Uberaba River Basin’s water resources, seeking the maintenance of its quality and rational use.⁹ Uberaba is inserted in the plateau of the Paraná Basin – Bauru Sub-basin, characterized by the incidence of tablelands and scarps. Geology is dominated by the presence of the Uberaba and Marília formations, belonging to the Bauru Group, overlaying the basaltic rocks belonging to the Serra Geral Formation. Involving the Marília Formation are the Cenozoic’s sediments attributed to the Nova Ponte Formation, which compose the municipality’s lands of higher altitudes and lower slope.¹⁰

According to the classification of Köppen, three climatic classes characterize the Triângulo Mineiro e Alto Paranaíba mesoregion: Aw (Tropical Wet and Dry or Savanna climate), Cwa (Subtropical-Dry Winter) and Cwb (Dry Winter Subtropical Highland climate). The Aw, which dominates 78% of this mesoregion, is characterized by a dry winter (May – September), presenting less than 40 millimeters of precipitation a month, and a rainy summer (October-March), with 60% of the annual rainfall concentrated in the months of November, December, January and February.¹¹. According to Brazilian system of soil classification, the most predominant soil units found in the catchment area of the Uberaba River are: the Latossolos, in the suborders Vermelho e Vermelho Amarelo; the Cambissolos, in the suborders Háplico and Húmico; the Gleissolos, in the suborder Melânico; the Neossolos, in the suborders Regolítico and Flúvico; the Argissolos, in the suborder Amarelo; and the Plintossolo, in the suborder Háplico.¹²

Data preprocessing

The preprocessing steps adopted in this study were carried out by using the ArcGIS software, based on a 30 meters resolution Digital Elevation Model (DEM) obtained from the Shuttle Radar Topography Mission (SRTM), developed by the National Aeronautics and Space Administration (NASA). The methodology is summarized in Figure 1 and explained subsequently. Initially the Fill tool, available in the Spatial Analyst toolbox, was used to fill the DEM’s surface depressions and to eliminate its imperfections, thereby generating the Hydro DEM of the study area. Afterwards the Flow Direction tool, run with the D8 method (Figure 2), was used to generate a raster which assigns a flow from each cell to one of its eight neighboring pixels, either adjacent or diagonal, in the direction of the steepest downward slope.¹³ Based on the flow direction grid, the Flow Accumulation tool was used to generate a new grid (Figure 3) which gives the flow as the sum of the amount of water flowing into each downslope cell.¹³ Subsequently, the Set Null tool was run in order to create a raster with the drainage network, by using the condition "Value <1000", and thus considering 1000 cells as the threshold of contributing pixels. To convert the raster network into a vector the Stream to Feature tool was used. Based on the hydrological, topological and pedological features of the study area, the subbasins’ outlets were created for each level of spatial discretization under study and its delineations (Figure 4-11) were obtained running the Watershed tool.

Figure 1 Preprocessing steps flowchart.

Figure 2 Flow direction coding.

Figure 3 Flow accumulation coding.

Figure 4 2 Subbasin configuration.

Hydrological modeling (HEC-HMS)

Developed by the Hydrologic Engineering Center (HEC) of the United States Army Corps of Engineers (USACE), the Hydrologic Modeling System (HEC-HMS) is a software that contains an array of mathematical models designed to simulate the hydrologic processes of watershed systems, such as rainfall, snowmelt, evapotranspiration, infiltration, excess precipitation transformation, baseflow and stream routing.¹⁴ The HEC-HMS it is one the most widely used and documented hydrological model, run several different studies.^15-18

Input data

Daily stream flow data from 1995 through 2017 was acquired from the Uberaba gage station, available at ANA’s portal HIDROWEB. Precipitation data for the same period was obtained at a daily time step from the station 83577 - UBERABA - MG (19°43'48.0"S; 47°57'00.0" W), available at the Meteorological Database for Education and Research ( BDMEP - Banco de Dados Meteorológico para Ensino e Pesquisa) belonging to the Brazilian National Institute of Meteorology (INMET – Instituto Nacional de Meteorologia). The physiographic parameters required by the adopted models, such as area, channel length, slope and curve number, were derived from each subbasin in the ArcGIS environment, for the five levels of discretization under study.

Loss model

Precipitation losses, which occurs through the runoff /infiltration processes, was determined using the SCS Curve Number method. The method calculates the effective precipitation of a hydrological event based on an empirically derived relationship between location, soil-type, land use, antecedent moisture conditions and runoff (Eq. 1).¹⁴

$P_e=\frac{{(P-0,2.S)}^2}{P+0,8.S}$                                                                                                  (1)

Where: P_e, accumulated precipitation excess at time t; P, accumulated rainfall depth at time t; S, potential maximum retention. The initial abstraction (Ia) was estimated as a constant 20% of the maximum potential retention S, as recommended by the Technical Reference Manual.¹⁴ The curve number (commonly abbreviated CN) is an intermediate parameter, which relates the maximum retention, and the watershed characteristics (Eq. 2). The CN values, ranging from 0 to 100, were estimated based on the tables published by the SCS and knowledge of the soil type and land use of the study area.

$S=\frac{25400-254.CN}{CN}$                                                             (2)

Considering that Brazilian soils do not fit the SCS’s hydrological groups descriptions, it was adopted a new classification proposal.¹⁹ This classification takes into account not only the soil’s texture, but also its characteristics and profile, reducing the modeler’s doubts.²⁰ Although this classification was created based on soils situated in the State of São Paulo, it can be applied throughout Brazil where similar soils occur.²¹ The CN Map (Figure 5) was generated based on the data of the Land Use and Occupation Map (Figure 6), created by Uniube’s Geoprocessing Laboratory, and the Soil Map (Figure 7), adapted from the Soil Map of the State of Minas Gerais.²²

Figure 5 4 Subbasin configuration.

Figure 6 8 Subbasin configuration

Figure 7 16 Subbasin configuration.

Figure 8 32 Subbasin configuration.

Figure 9 Curve Number Map.

Figure 10 Land Use and Occupation Map.

Figure 11 Soil Classification Map.

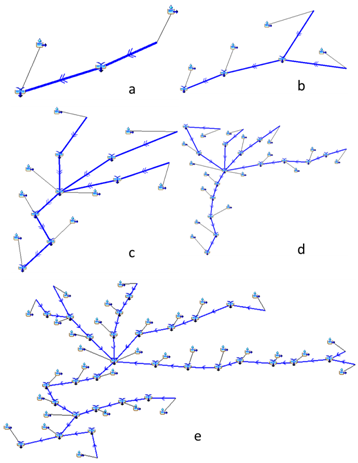
Figure 12 Distinct model configurations with diferent number of subbasins: two subbasins in a, four in b, eight in c, sixteen in d and thirty-two in e.

Figure 13 Calibration (a) and validation (b) curves.

Transform method

To simulate the process of direct runoff of excess precipitation on the watershed it was adopted the SCS Unit Hydrograph, which estimates the Unit Hydrograph (UH) peak discharge (Eq. 3) and the time of peak (Eq. 4).¹⁴

$U_P=C\frac{A}{T_P}$                             (3)

$T_P=\frac{\Delta t}{2}+t_{lag}$                                         (4)

Where: UP = UH peak; A = watershed area; C = conversion constant (2.08 in SI); TP = time of peak; Δt = the excess precipitation duration; tlag= the basin lag, corresponding as 60% of the time of concentration (Tc).

The performance evaluation of 22 Tc formulas indicates the Bransby-Williams is the most suitable method for large watershed.²³ As such, the Tc was determined using the Bransby-Williams formula (Eq. 5).

$Tc=\mathrm{58.5.}L.A^{-0.1}-S^{-0.2}$                                       (5)

Where: L = mainstream length; A = catchment area; S = equal area slope.

ainstream length, km

A=Catchment area, km²

S=Equal Area Slope, m/km

Routing method

To calculate the downstream outflow hydrograph, given an upstream hydrograph as a boundary condition, it was selected the Muskigum-Cunge routing method. This method uses a finite difference approximation of the partial derivatives of the continuity equation and the diffusion form of the momentum equation to generate the Eq. 6.¹⁴

$O_t=C_1{I}_{t-1}+C_2{I}_t+C_3{O}_{t-1}+C_4(q_L\Delta x)$                                            (6)

The coefficients are:

$C_1=\frac{\raisebox{1ex}{$\Delta t$}\!\left/ \!\raisebox{-1ex}{$k$}\right.+2X}{\raisebox{1ex}{$\Delta t$}\!\left/ \!\raisebox{-1ex}{$k$}\right.+2(1-X)}$                                                            (7)

$C_2=\frac{\raisebox{1ex}{$\Delta t$}\!\left/ \!\raisebox{-1ex}{$k$}\right.-2X}{\raisebox{1ex}{$\Delta t$}\!\left/ \!\raisebox{-1ex}{$k$}\right.+2(1-X)}$                                             (8)

$C_3=\frac{2(1-X)-\frac{\Delta t}{k}}{\frac{\Delta t}{k}+2(1-X)}$                                              (9)

$C_4=\frac{2\left(\frac{\Delta t}{k}\right)}{\frac{\Delta t}{k}+2(1-X)}$                                              (10)

Where: K= travel time of the flood wave through routing reach; X= attenuation of the flood wave; ∆t = time step.

In which the parameters K and X are:¹⁴

$K=\frac{\Delta x}{c}$                               (11)

$X=\frac{1}{2}\left(1-\frac{Q}{B{S}_{o}c\Delta x}\right)$                    (12)

Where: Q = reference flow; B = top width of the water surface; So= friction slope or bed slope; c= wave celerity (speed); Δx= the length of reach.

Model calibration

Based on several simulations, the event of greater adherence was selected for the calibration period, comprised between 1st of November 2003 and the 31st of December 2003. In this step, the objective function Sum of squared residuals (Eq.13) and the Univariate-Gradient search algorithm were adopted in order to obtain the best fit between the observed and calculated flow values.

$Z={{\displaystyle {\sum }_{i=1}^{NQ}\left[q_o(i)-q_s(i)\right]}}^2$ (13)

Where: Z= objective function; NQ= number of computed hydrograph ordinates; q_o=observed flows; q_s=calculated flows.

Model validation

The validation period, comprised between comprised between 1st of November 2004 and the 31^st of December 2004, was selected to verify the reliability of the calibration.

Model performance evaluation

To evaluate the performance of the hydrological model it was used the hydroGOF package, within the R software environment, to calculate seven goodness-of-fit measures: Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), RMSE-observations standard deviation ratio (RSR), Nash-Sutcliffe Efficiency (NSE), Percent Bias (PBIAS), Coefficient of Determination (R2) and Kling-Gupta Efficiency (KGE). The MAE (Eq. 14) records in real units the level of agreement between the observed and modelled datasets, evaluating all the deviations from the observed values, without considering the magnitude of the event. It is a non-negative metric that indicates a perfect simulation when the result is zero.²⁴

$MAE=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n|Q_{obs}-Q_{sim}|}$                                                                                                                              (14)

Where: n= number of samples; Qobs = observed flow; Qsim = simulated flow.

The RMSE (Eq. 15) computes on squared differences the mean magnitude of the error between the observed and modeled values, in which the largest deviations contribute the most. Zero indicates a perfect fit between the simulated and observed data.²⁴

$RMSE=\sqrt{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n|Q_{obs}-{Q_{sim}|}^2}}$                                              (15)

The RSR (Eq. 16) is calculated as the ratio of the RMSE and the standard deviation of measured data. It varies from 0 to ∞, in which the lower the RSR value the better the hydrological model performance.²⁵

$RSR=\frac{\sqrt{{\displaystyle {\sum }_{i=1}^n|Q_{obs}-{Q_{sim}|}^2}}}{\sqrt{{\displaystyle {\sum }_{i=1}^n|Q_{obs}-{\overline{Q_{obs}}|}^2}}}$                                   (16)

Where  represents the mean of the observed data;

The NSE (Eq. 17) has been widely used to evaluate the performance of hydrological models.²⁶ It ranges from -∞ and 1, with the NSE=1 indicating a perfect fit between simulated and observed data. Values between 0 and 1 are generally regarded as acceptable levels of performance, while values ≤0 suggests unacceptable performance.²⁴

$NSE=1-\left[\frac{{\displaystyle {\sum }_{i=1}^n{(Q_{obs}-Q_{sim})}^2}}{{\displaystyle {\sum }_{i=1}^n{(Q_{obs}-\overline{Q_{obs}})}^2}}\right]$                             (17)

The PBIAS (Equation 18) evaluates the average tendency of the simulated values to be higher or lower than those observed. The ideal value of PBIAS is 0; positive values indicate a model bias toward underestimation; and negative values indicate a bias toward overestimation.²⁷

$PBIAS=100x\left[\frac{{\displaystyle {\sum }_{i=1}^n(Q_{obs}-Q_{sim})}}{{\displaystyle {\sum }_{i=1}^n(Q_{obs})}}\right]$ (18)

General model evaluation guidelines for systematic quantification of accuracy in watershed simulations were created based on RSR, NSE and PBIAS performance ratings.24 These values are presented in Table 1.

The R2 (Eq. 19) records as a ratio the proportion of the total statistical variance in the observed dataset that can be explained by the model. It varies from 0 (poor model) to 1 (perfect model).²⁷

$R^2={\left[\frac{{\displaystyle {\sum }_{i=1}^n(Q_{obs}-\overline{Q_{obs}})(Q_{obs}-\overline{Q_{sim}})}}{{\displaystyle {\sum }_{i=1}^n{(Q_{obs}-Q_{sim})}^2{\displaystyle {\sum }_{i=1}^n{(Q_{sim}-\overline{Q_{sim}})}^{{}^2}}}}\right]}^2$                                                   (19)

In which  represents the mean of the simulated data.

The KGE (Eq. 20) is based on the decomposition of the Nash-Sutcliffe coefficient and the Mean Squared Error (MSE) into three different terms that represent the bias, the correlation and a measure of relative variability in the simulated and observed values. Analogously to the NSE, the KGE ranges from -∞ to 1, with an ideal value of 1.²⁸

$KGE=1-\sqrt{{(r-1)}^2+{(\alpha -1)}^2+{(\beta -1)}^2}$                            (20)

Where  represents the Pearson’s correlation coefficient, α is the ratio between the mean simulated and mean observed flows and β represents the bias.

It was adopted five distinctive basin model configurations in the HEC-HMS desktop (Figure 12), in order to represent the watershed under study. In which: the subbasins are represented by a reservoir with an inlet and an outlet; lines represent the channels, with arrows indicating the flow direction; and a reservoir with two inlets and an outlet represents the junction of different elements. Based on the qualitative analysis of the simulated (Qsim) and observed (Qobs) hydrographs generated for the calibration and validation period (Figure 13), it can be noted that although the calculated hydrographs underestimate the peak flow magnitudes of the observed hydrographs, the overall fit of the model is good, indicating the model represents the hydrological processes in the watershed efficiently. It can also be noted the modeled hydrographs overlap each other, showing no significant change, thus demonstrating that different levels of spatial discretization did not interfere in the watershed’s outlet flow.

The obtained values from the goodness-of-fit tests (Table 2) indicate that there is a good fit between the simulated and observed data for both periods, regardless of the number of sub-basins. And although the different lef discretization did not significantly affect the HEC-HMS model’s performance, the 4 sub-basin configuration stood out by showing superior performance in the calibration period, since it presented the best values of RMSE, NSE and PBIAS, and inferior performance in the validation period, where the worst values of MAE, RMSE and NSE were presented. This happens in a similar way with the 32 sub-basin configuration, which presents the worst performance in the calibration phase due to its values of RMSE, NSE, R2 and KGE, and the best performance in the validation phase, due to its values of MAE, RMSE, PBIAS and R2.

Similar studies support the qualitative and quantitative analysis results, indicating the level of spatial discretization does not significantly affect the model’s performance.^6,29,30 This can be explained by the watershed similar physiographic characteristics (such as slope, land use and occupation and soil types), that result in model’s standardization.³¹ As such, the process of watershed spatial discretization should always consider the presence of a reservoir in a tributary channel, the significant difference in the level of urbanization, or the significant difference in physiographic characteristics.²⁹ Moreover, the homogeneity of outcomes no matter the subbasins configuration, may have been influenced by the intrinsic deterministic nature of the HMS models and the use of only one discharge station to evaluation the simulation results.^32,33

The performance of the HEC-HMS model in both periods, calibration and validation, highlights its ability to properly represent the watershed’s processes, regardless of the level of spatial discretization. This study emphasizes the level of spatial discretization does not substantially influence the HEC-HMS model’s performance without significant differences in the watershed physiographic characteristics (slope, land use and types of soil). Considering its good performance, the HEC-HMS model can be reliably applied to future works that aim to study the drainage capacity of the APA of the Uberaba River Basin, in order to subsidize public policy proposals for land use and occupation that aim to prevent flooding issues like those that the city of Uberaba faces today.

None.

The authors declare that there is no conflict of interest.

Nonel.

1. Tucci CEM. Hydrology: science and application. 4th edn. UFRGS/ABRH Publisher, Porto Alegre. 2012.
2. Braud JA. Impact of watershed delineation detail on hydrologic process modeling in low slope areas Recommended Citation. Louisiana State University and Agricultural and Mechanical College. 2009.
3. Almeida L, Serra JCV. Most used hydrological models, types and applications. Rev da FAE. 2017;20:129–137.
4. Bingner RL, Garbrecht J, Arnold JG, et al. Effect of watershed subdivision on simulation runoff and fine sediment yield. Trans ASAE. 1997;40:1329–1335.
5. Jha M, Gassman PW, Secchi S, et al. Effect of watershed subdivision on swat flow, sediment, and nutrient predictions. J Am Water Resour Assoc. 2004;40:811–825.
6. Baduna Koçyiğit M, Akay H, Yanmaz AM. Effect of watershed partitioning on hydrologic parameters and estimation of hydrograph of an ungauged basin: a case study in Gokirmak and Kocanaz, Turkey. Arab J Geosci. 2017;10:331.
7. Zhang HL, Wang YJ, Wang YQ, et al. The effect of watershed scale on HEC‒HMS calibrated parameters: A case study in the Clear Creek watershed in Iowa, US. Hydrol Earth Syst Sci. 2013;17:2735‒2745.
8. Casey MJ, Stagge JH, Moglen GE, et al. Effects of Watershed Subdivision on Peak Discharge in Rainfall‒Runoff Modeling in the WinTR‒20 Model. J Hydrol Eng. 2015;20:04015020.
9. UBERABA. Law No. 9,892, of December 28, 2005. Creates the Uberaba Municipal Environmental Protection Area ‒ Uberaba River APA ‒ and makes other arrangements. Porta Voz no 605, Uberaba. 2006.
10. Schobbenhaus C, Silva CR da. Geoparks of Brazil: proposals. CPRM, Rio de Janeiro. 2012.
11. Sá Júnior A de. Application of the Köppen classification for the climatic zoning of Minas Gerais State. Federal University of Lavras. 2009.
12. Pedroso Neto JC. Soils of the Uberaba River Basin. 1st edn. Del Rey Graphic Designer Ltda, Belo Horizonte. 2013.
13. Molina G, Gaber A, El‒Baz F. Mapping palaeolakes in the Ténéré Desert of northeastern Niger using space‒borne data for groundwater potential. NRIAG J Astron Geophys. 2017;6(2):395–407.
14. USACE. Hydrologic Modeling System HEC‒HMS Technical Reference Manual. Tech Ref Man. 2000.
15. Rezaeianzadeh M, Stein A, Tabari H, et al. Assessment of a conceptual hydrological model and artificial neural networks for daily outflows forecasting. Int J Environ Sci Technol. 2013;10:1181–1192.
16. Gumindoga W, Rwasoka DT, Nhapi I, et al. Ungauged runoff simulation in Upper Manyame Catchment, Zimbabwe: Application of the HEC‒HMS model. Phys Chem Earth. 2017;100:371‒382.
17. Wu R‒S, Dong‒Sin S. Modeling Hydrological Impacts of Groundwater Level in the Context of Climate and Land Cover Change. Terr Atmos Ocean Sci. 2018.
18. De Moraes TC, Dos Santos VJ, Calijuri ML, et al. Effects on runoff caused by changes in land cover in a Brazilian southeast basin: evaluation by HEC‒HMS and HEC‒GEOHMS. Environ Earth Sci. 2018;77:250.
19. Sartori A, Genovez AM, Lombardi Neto F. Hydrological Classification of Brazilian Soils for Over‒Rain Estimation with the US Soil Conservation Service Method Part 2: Application. RBRH. 2005a.
20. Sartori A, Lombardi Neto F, Maia Genovez A. Hydrological Classification of Brazilian Soils for Estimating Excess Rain using the US Soil Conservation Service Method Part 1: Classification. RBRH. 2005b.
21. Damé RDCF, Teixeira CFA, Siqueira G do A, et al. CN parameter estimation and impact of urbanization in a southernmost basin of Brazil. In: XIV World Water Congress. Porto de Galinhas. 2011.
22. UFV UF de V. Map of Soils of the State of Minas Gerais. State Environmental Foundation, Belo Horizonte. 2010.
23. Salimi ET, Nohegar A, Malekian A, et al. Estimating time of concentration in large watersheds. Paddy Water Environ. 2017;15(1):123–132.
24. Dawson CW, Abrahart RJ, See LM. HydroTest: A web‒based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ Model Softw. 2007;22:1034–1052.
25. Moriasi DN, Arnold JG, Van Liew MW, et al. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans ASABE. 2007.
26. Brighenti TM, Bonumá NB, Chaffe PLB. Hierarchical Calibration of SWAT model for a watershed in southern Brazil. Rev Bras Recur Hídricos. 2016;21(1):53–64.
27. Gupta HV, Sorooshian S, Yapo PO. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J Hydrol Eng. 1999;4:135–143.
28. Gupta HV, Kling H, Yilmaz KK, et al. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J Hydrol. 2009;377(1‒2):80–91.
29. Thompson DB, Cleveland TG. Subdivision of Texas watersheds for hydrologic modeling. Texas Tech University. College of Engineering, Texas. 2009.
30. Nandalal HK, Ratmayake UR. Event Based Modeling of a Watershed Using HEC‒HMS.Eng J Inst Eng Sri Lanka. 2010;43:28.
31. Wallace CW, Flanagan DC, Engel BA. Evaluating the effects of watershed size on SWAT calibration. Water (Switzerland). 2018;10(7):898.
32. Cabral SL, Sakuragi J, Silveira CDS. Uncertainties and errors flow estimate using hydrological modelling and precipitation by RADAR. Ambient e Agua ‒ An Interdiscip J Appl Sci. 2017;12(1):57.
33. Derdour A, Bouanani A, Babahamed K. Hydrological modeling in semi‒arid region using HEC‒HMS model. case study in Ain Sefra watershed, Ksour Mountains (SW‒Algeria). J Fundam Appl Sci. 2017.