Half-hourly values of turbulent sensible (H) and latent (LE) heat fluxes, net radiation (𝑄^∗) at the surface, and heat store in the canopy (𝛥𝑄_𝑆) are used to characterize seasonal and interannual changes during three not-consecutive years (2009–12) in a suburban area (LCZ 6) of the megacity of São Paulo. Turbulent fluxes are estimated applying eddy covariance method to turbulence measurements performed with sampling rate of 10 Hz, between 25 and 26 m above the surface, and enforcing quality control procedures. The diurnal evolution of monthly average hourly values of 𝐻, 𝐿𝐸, 𝑄^∗ and 𝛥𝑄_𝑆 observed in 2012 indicate a seasonal variation with a daytime maximum with 𝐻 varying from a maximum of 180 ± 12 W m^-2 in October to a minimum of 80.1 ± 9 W m² in June, 𝐿𝐸 varying from a maximum of 152.0 ± 7.6 W m^-2 in February to a minimum of 66.4 ± 7.6 W m^-2 in September, -𝑄^∗ varying from a maximum of 554 ± 14 W m^-2 in February to a minimum of 369±13 W m^-2 in July, and -𝛥𝑄_𝑆 varying from a maximum of 249± 47 W m^-2 in April to a minimum of 181 ± 58 W m^-2 in July. Monthly average daily values of H, LE and 𝑄^∗ corroborate seasonal pattern displayed by monthly average hourly values, with maximum of 5 ± 0.5 MJ m^-2 day^-1 for H and 5.3 ± 0.6 MJ m^-2 day^-1 for LE in November (summer), and minimum of 1.3 ± 0.2 MJ m^-2 day^-1 for H in June and 1.9 ± 0.2 MJ m^-2 day^-1 for LE in August. −𝑄^∗ shows a maximum of 11.6 ± 1.1 MJ m² day^-1 in March and a minimum of 4.5±0.9 MJ m^-2 day^-1 in June. Similar patterns was observed during 2009 and 2010. An empirical model based on Modified Priestly-Taylor Method coupled to Objective Hysteresis Method was validated with observations carried out during May and June (2009–2010, 2012) and applied successfully to estimate monthly average hourly values of 𝐻, LE and 𝛥𝑄_𝑆 during February–April and August–Novemb 2012.

Keywords: sensible heat flux, latent heat flux, São Paulo megacity, surface energy balance, modified Priestley-Taylor method, objective hysteresis method

Highlights

1. Unique set of turbulence and net radiation data, covering measurements during 3 years span (2009, 2010 and 2012), was used to estimate 15 months of half-hourly values of vertical turbulent fluxes of sensible (H) and latent heat (LE), net radiation (𝑄^∗) at the surface, and heat store in the canopy (𝛥𝑄_𝑆) in a suburban area (LCZ 6) of the megacity of São Paulo.
2. Seasonal variation of monthly average daily values of H and LE are close related to -𝑄^∗, with maximum H = 5 ± 0.5 MJ m^-2 day^-1 and LE = 5.3 ± 0.6 MJ m^-2 day^-1 in November (summer), and a minimum H = 1.3 ± 0.2 MJ m^-2 day^-1 in June (winter) and LE = 1.9 ± 0.2 MJ m^-2 day^-1 in August (winter). −𝑄^∗ shows a maximum of 11.6 ± 1.1 MJ m^-2 day^-1 in March and a minimum of 4.5 ± 0.9 MJ m^-2 day^-1 in June.
3. Empirical model, based on the Modified Priestly-Taylor Method coupled with the Objective Hysteresis Method, was validated to estimate monthly average hourly values of H, LE and 𝛥𝑄_𝑆 in a suburban area of the megacity of São Paulo, using as input only monthly average hourly values of 𝑄^∗ and air temperature.

MRSP, metropolitan region of São Paulo megacity; SEB, surface energy balance; 𝑄^∗, net radiation; 𝑄_𝐹, anthropogenic heat; H, energy flux of sensible heat; LE, energy flux of latent heat; 𝛥𝑄_𝑆, heat store in the urban canopy; S, residue; S, (𝑑𝑞⁄𝑑𝑇)_s; q, specific humidity; IBGE, Brazilian Institute of Geography and Statistic; UHI, urban heat island; UBL, urban boundary layer; MCITY, MegaCITY; BIOMASP, BIOgenic emissions, chemistry and impacts in the Metropolitan Area of São Paulo; ECM, eddy covariance method; USP, University of São Paulo; PM, micrometeorological platform ("Plataforma Micrometeorológica"); IAG, Institute of Astronomy, Geophysics and Atmospheric Sciences of USP; $\rho ,$ air density (kg m^-3); cp, specific heat at constant pressure of the air (1004 J K^-1 kg^-1); L_V, water vapor latent heat (2500 J kg^-1), $\left(\overline{T\text{'}W\text{'}}\right),$  covariance between turbulent fluctuations of air temperature and vertical components of wind (Kms^-1); $\left(\overline{w\text{'}{\rho }_v\text{'}}\right)$ Covariance between turbulent fluctuation of vapor density and vertical components of wind (mg m s^-1); µ, M_a/M_v; M_a molar mass for dry air (28.97 kg Kmol^-1); M_v, molar mass for water vapor (18.02 kg Kmol^-1); $\sigma ,$ ${\rho }_v/{\rho }_a$ ; ${\rho }_a,$ dry air density; ${\rho }_v,$  water vapor density; Β, Bowen ratio; PTM, Priestly-Taylor method; MPTM, modified Priestly-Taylor method; H_S, saturation energy flux of sensible heat; LE_S, saturation energy flux of latent heat; ${\alpha }_{PT}$ , Priestley-Taylor constant; 𝛼^′, modified Priestley-Taylor constant; 𝛽^′, constant factor urban SEB model; OHM, objective hysteresis method; a₁, OHM constant (0.56); a₂, OHM constant (0.46 hours); a₃, OHM constant (-37.75 W m^-2)'; M_i, modeled value; O_i, observed value; N, total number of values; MBE, mean bias error; RMSE, root mean square error; FAPESP, state of São Paulo research foundation; FAPERJ, state of Rio de Janeiro research foundation; CNPq, Brazilian national council for scientific and technological development; CAPES, coordination for the improvement of higher education personnel

The interaction between surface and atmosphere in urban areas can be described by the temporal and spatial variation of the surface energy balance (SEB) components (Eqn. 1). Knowing the SEB components is important to understand the role play by cities on the urban climate^1,2 and, to objectively establish actions to mitigate the adverse effects induced by urbanization.³ This knowledge is particularly vital in Brazil, where more than 85% of population lives in urban areas.⁴ The SEB in urban areas can be expressed as:

$Q*+Q_F+H+LE=\Delta Q_S+\Delta Q_A+S$   (1)

where 𝑄^∗ is the net radiation, 𝑄_𝐹 anthropogenic heat, 𝐻 and 𝐿𝐸 are respectively the vertical turbulent fluxes of sensible and latent heat, respectively, 𝛥𝑄_𝑆 is the heat stored in the urban canopy, 𝛥𝑄_𝐴 horizontal advection of heat and 𝑆 is the residue. By convention, in this work upward energy fluxes are positive and vice versa.

In most studies carried out in urban areas, only three terms of Eqn. 1 are estimated directly through observations: 𝑄^∗, 𝐻 and 𝐿𝐸.^5,6 All other terms are estimated indirectly; 𝑄_𝐹 is estimated as a residual of SEB⁷ or by inventory methods;^8,9 𝛥𝑄_𝑆 is also estimated as a residual of Eqn. (1) whenever independent estimates of 𝑄^∗, 𝐻, 𝐿𝐸 and 𝑄_𝐹 are available.¹⁰ Alternatively, and as it will be explored in this work, 𝛥𝑄_𝑆 is evaluated in terms of 𝑄^∗ and land use features using empirical relationship.^11,12 In general, 𝛥𝑄_𝐴 is neglected in observational investigations of SEB, therefore the role of this term is not well documented in the literature.¹³ and, for this reason it will not be considered in this work.

The classification of land use is a fundamental information in studies involving estimates of SEB components in cities. Most of these studies use the traditional classification based on three categories: urban, suburban and rural.⁶ Recently, a more complete classification of land use in cities become available.¹⁴ Known as the Local Climate Zone (LCZ), it is made up of 17 categories: 10 indicate built-up areas, 4 vegetation, 2 bare soil and 1 water. Although expanding the land use type from 3 to 17 increases the accuracy of describing cities' land use, applying the LCZ to Brazilian cities may not be straightforward because the LCZ reflects typical characteristics of American and European cities, which differ significantly from most Brazilian cities. Furthermore, both data analysis and modeling can benefit from the 3-category classification, as there is a larger body of observational and modeling work available in the literature that uses this type of land use classification. Therefore, in this work the traditional land use classification will be used as a reference to analyze the seasonal and interannual variations of the SEB components and develop an empirical model to simulate them for suburban areas of the megacity of São Paulo.

Although 𝐻 and 𝐿𝐸 in São Paulo Megacity (23º30'S, 46º40'W, 760 m) follow diurnal patterns like cities at higher latitudes, there are some differences in the portioning of other SEB components. The SEB components estimated during Autumn 2009 indicate that 𝛥𝑄_𝑆 corresponds to approximately 50% of 𝑄^∗.¹²

Using the inventory method for the megacity of São Paulo, Ferreira et al.¹⁵ found that 𝑄_𝐹 presents a bimodal diurnal evolution, mainly associated with daytime vehicular heat emission, with average maximum of 20 W m^-2. This diurnal pattern remains relatively constant throughout the year and can be considered small compared to mid-latitude cities, especially during winter. Despite this, Ribeiro et al.¹⁶ found that the Weather Research and Forecast model yields more realistic numerical simulations of UHI intensity and UBL height when 𝑄_𝐹 amplitude of 20 W m^-2 is partitioned into 11.2 W m^-2 for low density residential fraction (66.4%), 33.5 W m^-2 for high-density residential fraction (29.9%), and 70 W m^-2 for commercial/industrial fraction (3.7%). More recently, Oliveira et al.¹⁷ documented significant and unexpected spatial variations of SEB components among urban, suburban, and rural sites in the metropolitan region of São Paulo Megacity (MRSP), using observations made during the MCITY BRAZIL project´s 10-day winter field campaign in August 2013. The observations carried out during the 2023 intensive field campaign of BIOMASP+ project corroborate SEB observations made earlier in 2013 (Oliveira, 2023).¹⁸

As shown above, understanding the behavior of SEB components is essential to determine how land use modulates the input of energy into the atmosphere and regulates the climate in urban areas, to develop mitigation actions to reduce the adverse effects of urbanization on the climate. In the case of Brazil there are very few observational works that provide information such as SEB components with quality enough and duration suffice to achieve this goal.¹⁷ Despite the encouraging observational and modeling results described in previous paragraph, more accurate and long-term estimates of SEB components, reflecting local features of the urban fabric and vegetation, are still necessary in the case of MRSP, as well as for other Brazilian larger conurbations.

Therefore, the present study aims to use observed values of 𝐻, 𝐿𝐸, 𝛥𝑄_𝑆 and 𝑄^* to:

1. Characterize the seasonal and interannual variations of 𝐻, 𝐿𝐸, 𝛥𝑄_𝑆 and 𝑄^* during 2009, 2010 and 2012.
2. Validate an empirical model, based on Modified Priestly-Taylor Method (MPTM) coupled to Objective Hysteresis Method (OHM), to estimate monthly average hourly values of 𝐻, 𝐿𝐸 and 𝛥𝑄_𝑆 in a suburban area of the megacity of São Paulo.

To achieve these goals, half-hourly values 𝐻, 𝐿𝐸 and 𝑄^* are estimated directly, by applying eddy covariance method to turbulence measurements performed with a sampling frequency of 10 Hz (𝐻, 𝐿𝐸) and by averaging 𝑄^* measurements performed with a sampling frequency 0.05 Hz. Half-hourly values 𝛥𝑄_𝑆 are estimated, simultaneously to 𝐻, 𝐿𝐸 and 𝑄^*, as residue of SEB Eqn. (1) neglecting 𝑄_𝐹 and 𝛥𝑄_𝐴. All measurements were carried out in a suburban site, located on the campus of the University of São Paulo (USP), in a 10-m tower at the top of a 4-story building, hereinafter indicated by PM IAG, during 31 days in 2009 (~1 month), 115 days in 2010 (~4 months) and 303 days in 2012 (10 months). Major features of observations, eddy covariance technique, footprint analysis and empirical modelling formulation are described in section 2. Seasonal and interannual variations of 𝐻, 𝐿𝐸, 𝑄^∗, 𝛥𝑄_𝑆 and MPTM-OHM model validation for the megacity of São Paulo are discussed in section 3. Major results are summarized in the conclusion.

Observation

High-frequency measurements (10 Hz) of vertical wind speed (𝑤), air temperature (𝑇) and water vapor density (𝜌_𝑣) were carried out by a set of turbulence sensors (Table 1) in a 10-m height micrometeorological tower located at the Micrometeorological Platform (PM IAG). This platform is 17 m above the ground at the top of the 4-story building of the Institute of Astronomy, Geophysics and Atmospheric Sciences (IAG), in the Butantã Campus of the University of São Paulo (USP), west São Paulo Megacity. Between 2009 and 2012 turbulence sensors were set at 26.0 m and 25.4 m above surface, respectively (Figure 1). In 2010 only sonic anemometer was available at 26.0 m above surface. According to Ferreira et al.,¹² within a 1-km radius area centered in the PM IAG, the surface is occupied by 25.4% of trees, 64.1% of impervious building and streets, 7.3% by grass, shrub, and scrub, and 2.3% of water, indicating a suburban land use around the PM IAG (Figure 1). The 1-km radius area is characterized by LCZ 6, confirming the earlier classification performed by Ferreira et al.,¹² Oliveira et al.,¹⁷ and Silveira et al.¹⁹

The topography is gently sloping towards the Pinheiros river valley, with elevations ranging from 718 m in the north to 782 m in the south (Figure 1a). Most buildings have 3-4 floors, sparsely distributed, with an average height of 6.6 m (Figure 1b). According to Silveira et al.¹⁹ this area is characterized by roughness length equal to 0.52 ± 0.17 m and zero-plane displacement 15.0 ± 3.1 m. Therefore, between 2009 and 2012 turbulence measurements were performed majority at heights above the roughness sublayer (Table 1). Turbulence, net radiation, and air temperature measurements simultaneously cover the following periods: May 18 to June 17, 2009; March 8 and June 30, 2010; and February 1 to November 30, 2012. Considering these periods, it was possible to single out 27 days in 2009, 38 days in 2010 and 245 days in 2012 of continuous observation.

Figure 1 (a) IAG-building landscape and (b) 10-m tower of the PM IAG looking west.

Eddy covariance method

Vertical turbulent fluxes of 𝐻 and LE are estimated from the eddy covariance method (ECM) based on the statistics fluctuation of vertical wind speed (𝑤^′), air temperature (𝑇^′) and water vapor density (𝜌_𝑣^′) with sampling frequency of 1 Hz or higher.^20,21

$H=\overline{\rho } c_p\overline{\left(w\text{'}T\text{'}\right)}$   (2)

$LE=H_V\overline{\left(w\text{'}\rho \nu \text{'}\right)}$   (3)

were is the mean air density, 𝑐_𝑝 the specific heat of air at constant pressure and 𝐿_𝑉 the water latent heat of evaporation. In Eqn. (2) and (3) the (̅ ̅) indicated mean values over 30-min interval and ( )^′ the statistical fluctuation of the mean.

The ECM provides the best way to estimate vertical turbulent fluxes if the average of the statistical fluctuations of air density and vertical wind speed are zero.²² In general, both considerations are not satisfied, to apply ECM is necessary to perform Webb correction in 𝐿𝐸 as indicated in Eqn. 4.

$LE=L\left(1+\mu \sigma \right)\left[\overline{\left(w\text{'}\rho \nu \text{'}\right)}+\frac{\overline{{\rho }_v}}{\overline{T}}\overline{\left(w\text{'}T\text{'}\right)}\right]$    (4)

where 𝜇 = 𝑀_𝑎/𝑀_𝑣, 𝑀_𝑎 is the molar mass for dry air (28.97 kg kmol^-1), 𝑀_𝑣 molar mass for water vapor (18.02 kg kmol^-1), $\sigma ={\rho }_v/{\rho }_a$  where ${\rho }_v$  and ${\rho }_a$  are water vapor and dry air densities.

In this work, half-hourly values of 𝐻 and 𝐿𝐸 are estimated using Eqns. (2) and (4) by considering dataset divided into 30-min consecutive blocks. Besides Webb correction, several quality control procedures were applied to estimate the 𝐻 and 𝐿𝐸 to remove glitches, linear trends, tower-blocking effects, signal saturation caused by rain and dew deposition on sonic transducers and gas analyzer windows, and to enforce skewness and kurtosis thresholds and stationarity.¹⁹ About 40% of the 30-min blocks were discard due to all these unwanted effects.

Footprint analysis

Footprint analysis of turbulence measurements carried out in PM IAG was performed using Flux Footprint Prediction model developed by Kljun et al.²³ The areas delimited by the footprint contour lines are centered on the PM IAG (Figure 2) and represent contributions to the measured 𝐻 and 𝐿𝐸 fluxes at this location ranging from 70% (areas delimited by the outermost contour line) to 10% (yellow areas). Annual footprint maps were estimated considering 30-min blocks of turbulence measurements satisfying all the quality control procedures described above. The maps indicated by 2009, 2010 and 2012 correspond respectively to the observations made on: May 18 to June 17, 2009 (Figure 2a); March 8 to June 30, 2010 (Figure 2c); and February 1 to November 30, 2012 (Figure 2e). The diurnal evolution of the UBL heights needed to estimate the footprint followed Silveira et al.¹⁹ The annual wind roses in Figure 2 correspond to wind observations made at PM IAG (Table 1) during the same period of turbulence measurements used to estimate the footprint. In general, the shape of footprint areas corresponding to 70% of contribution to the fluxes measured at PM IAG follows closely the most frequent wind direction distributions (Figure 2). In 2009, 70%-footprint area is elongated in the NNW-SSW axis induced by the most frequent wind directions from N-NNE and S-SSW sectors (Figure 2a–b). In 2010 and 2012 the 70%-footprint area elongated in the NW-SE axis induced in both years by the most frequent wind directions from NW and SE sectors (Figure 2c–f).

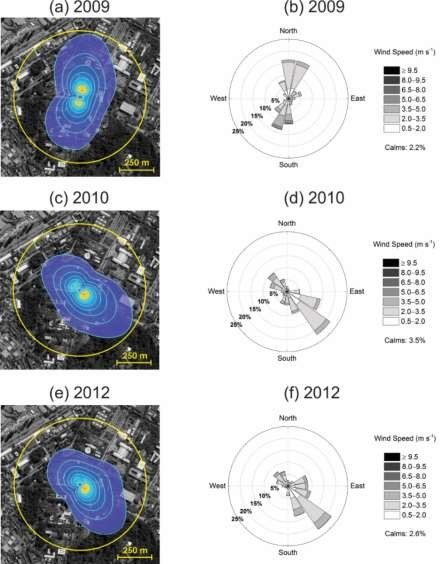
Figure 2 footprint maps and corresponding wind rose diagrams for (a)-(b) 2009, (c)-(d) 2010 and (e)-(f) 2012 in the PM IAG. Footprints obtained from Flux Footprint Prediction model.²³ Areas delimited by white lines in (a), (c) and (e) range from 10 (yellow) to 70% (blushed outermost) contribution to the turbulent fluxes measured in the center (PM IAG). Yellow circles in have radius equal to 500 m and land use photo was obtained from satellite (© CNES (2018) Distribution Airbus DS).

Empirical modeling of SEB components in urban areas

Both empirical models used here, MPTM and OHM, were initially developed to estimate 𝐻, 𝐿𝐸 and ∆𝑄_𝑠 on natural surfaces.^24–27 One of the first applications of the MPTM for urban areas was performed by Hanna and Chang (1992)²⁸ to estimate 𝐻 and 𝐿𝐸 in Indianapolis, Indiana, USA. They found that 𝐻 has a maximum discrepancy of 20% under high wind conditions. Grimmond and Oke²⁹ applied MPTM to estimate H and LE in 7 cities of North America with similar success. The OHM was adapted by Grimmond et al.¹¹ to estimate ∆𝑄_𝑠 and validated by Ferreira et al.¹² to the suburban region of São Paulo Megacity using measurements carried out in the PM IAG. In this work the MPTM will be validated and used to simulate monthly average hourly values of H and LE, in a suburban area of the megacity of São Paulo by coupling it to the OHM validated previously by Ferreira et al.¹²

Modified Priestley-Taylor method (MPTM)

This empirical model is based on an analytical solution of the following system of two linear equations: a) SEB equation for an ideal surface (plane, homogeneous and opaque to radiation) given by Eqn. (1) neglecting 𝑄_𝐹, 𝛥𝑄_𝐴, and S. and b) 𝛽 = 𝐻⁄𝐿𝐸, where 𝛽 is the Bowen ratio. The general solution for this system is: 𝐻 = −[𝛽⁄(1 + 𝛽)](𝑄^∗ − ∆𝑄_𝑠) and 𝐿𝐸 = −[1⁄(1 + 𝛽)](𝑄^∗ − ∆𝑄_𝑠). The resulting expressions for 𝐻 and 𝐿𝐸 can be further simplified by parameterizing them in terms of flux-gradient relationships assuming that the heat and water vapor diffusion coefficients are the same. Furthermore, by considering the atmosphere adjacent to the surface as saturated, the general solution for the SEB system yields saturation values of sensible (𝐻_𝑠) and latent heat (𝐿𝐸_𝑠) fluxes given by 𝐻_𝑆 = −[𝛾⁄(𝛾 + 𝑆)](𝑄^∗ − ∆𝑄_𝑠) and 𝐿𝐸_𝑠 = −[𝑆⁄(𝛾 + 𝑆)](𝑄^∗ − ∆𝑄_𝑠), where 𝛾 = 𝑐_𝑃⁄𝐿_𝑉 is the psychometric constant and 𝑆 = (𝑑𝑞⁄𝑑𝑇)_𝑠 the variation rate of specific humidity with respect to the air temperature under saturated condition. Priestley and Taylor²⁴ proposed corrections for 𝐻_𝑠 and 𝐿𝐸_𝑠 to estimate 𝐻 and 𝐿𝐸 for unsaturated conditions that satisfy the energy conservation principle. In this more realistic approach, 𝐿𝐸 is set equal to 𝛼_𝑃𝑇𝐿𝐸_𝑠 where 𝛼_𝑃𝑇 is a constant (Priestley-Taylor constant), greater than one, that depend on the surface and local climate conditions. The well-known Priestley-Taylor expressions become: 𝐻 = −(1 −𝛼_𝑃𝑇) [𝛾⁄(𝛾 + 𝑆)](𝑄^∗ − ∆𝑄_𝑠) and 𝐿𝐸 = −𝛼_𝑃𝑇[𝑆⁄(𝛾 + 𝑆)](𝑄^∗ − ∆𝑄_𝑠).

De Bruin²⁷ modified the Priestley-Taylor expressions above based on the observational fact that in most of the natural surfaces 𝐻 and 𝐿𝐸 do not tends to zero as 𝑄^∗ − ∆𝑄_𝑠 tends to zero. To accommodate this observational feature De Bruin²⁷ introduced a constant factor 𝛽^′ that takes into consideration that H tends to zero before 𝑄^∗ − ∆𝑄_𝑠 in the diurnal cycle s that:

$H=-\left(1-\alpha \text{'}\right)\frac{\gamma }{\gamma +S}\left(Q^{*}-\Delta Q_S\right)-\beta \text{'}$     (5)

$LE=-\alpha \text{'}\frac{S}{\gamma +S}\left(Q^{*}-\Delta Q_S\right)+\beta \text{'}$     (6)

where 𝛼^′ is the modified Priestley-Taylor constant.

Should be emphasized that De Bruin and Holtslag²⁶ demonstrated that the Priestley-Taylor expressions have the same skill as the Penman-Monteith expressions, which in turn were recognized as a more complete physical description of the surface atmosphere interactions.

Description of OHM

This method is based on the observational fact that ∆𝑄_𝑆 is related to 𝑄^∗ by:

$\Delta Q_S=a_1 Q^{*}+a_2\frac{d{Q}^{*}}{dt}+a_3$   (7)

where 𝑎₁, 𝑎₂ and 𝑎₃ are parameters obtained from land used analysis considering five categories: vegetated areas, pavement, roof, and canyons. According to Ferreira et al.¹² 𝑎₁, 𝑎₂ and 𝑎₃ equal to respectively 0.56, 0.46 hours and -37.75 W m^-2, produced the best fit between point clouds on a scatterplot of simulated ∆𝑄𝑠 (with OHM) versus estimated ∆𝑄𝑠 (as residuals of SEB equation using H, LE and Q* observed in the PM IAG).

Seasonal variation of diurnal evolution

The analysis of the seasonal variation of diurnal evolution is based on the monthly average hourly values of 𝐻, 𝐿𝐸, 𝑄^∗, and 𝛥𝑄_𝑆, observed in a suburban area of the megacity of São Paulo from February to November 2012 (Figure 3). The observations performed in 2009 (May 18 to June 17) and in 2010 (March 8 and June 30) are not displayed here but will be used to complement and expand this analysis.

Figure 3 Seasonal variation of monthly average hourly values of H, LE, ΔQs and Q* observed in the megacity of S�o Paulo during 2012. Vertical bars indicated the statistical error of monthly average hourly values.

During 2012, the amplitude of the diurnal cycle of 𝐻 varied from a maximum of 180 ± 12 W m^-2 in October to a minimum of 80.1 ± 9 W m^-2 in June. The amplitude of 𝐿𝐸 varies from a maximum of 152.0 ± 7.6 W m^-2 in February to a minimum of 66.4 ± 7.6 W m^-2 in September.

Similar patterns are observed in 2009 and 2010 with a tendency of 𝐻 and 𝐿𝐸 to increase in the wet-summer and decrease in the dry-winter months. In the case of 2010, 𝐻 displayed an amplitude maximum of 145.5 ± 8.9 W m^-2 in March and a minimum of 111.3 ± 7.1 W m^-2 in May. In 2009, 𝐻 (𝐿𝐸) displayed an amplitude maximum of 122 ± 26 W m^-2 (97 ± 16 W m^-2) in May and a minimum of 120 ± 15 W m^-2 (65.6 ± 5.9 W m^-2) in June.

Observations during both years were, restricted mostly to cold and dry months (May 18 to June 17, 2009; March 8 to June 30, 2010), explaining the differences in the seasonal variation of the amplitude of 𝐻 and 𝐿𝐸 between 2009-2010 and 2012. For 2009-2010 winter months prevailed clear sky conditions in the megacity of São Paulo favoring radiative heating of the surface and large incursions of positive values of H during daytime. Another effect that may be causing large values of H and LE observed in 2009 is footprint. Prevailing winds from SSW and NNE (Figure 2a) during May and June 2009 elongated the footprint shape in these directions (Figure 2b) covering a different land use area around PM IAG where predominates less vegetation compared to 2010 (Figure 2c) and 2012 (Figure 2e).

These seasonal variations indicate the amplitude of diurnal cycles of H are either similar or larger than LE in most of the months (Figure 3). During driest months (August-October) the amplitude of H is systematically larger than LE. Typical of suburban areas, this behavior occurs because the land use in 36% of the measurements site area is occupied by vegetation, responding to the seasonal variation of moisture in the megacity of São Paulo.^12,17,19

Throughout 2012, the amplitude of H and LE vary proportionally to 𝑄^∗. Both H and LE daytime maxima occur 1 hour after 𝑄^∗. In April, June, and November, H and LE maxima occur 2 hours after 𝑄^∗ (Figure 3c, e, j). According to Anandakumar,³⁰ the daytime lag between H and 𝑄^∗ are close related to the lag between air and surface temperature.

Another important feature of the SEB components observed in the megacity of São Paulo is the fact that the diurnal evolution of 𝛥𝑄_𝑆 are in phase with 𝑄^∗ in most of the months of 2012 (Figure 3).

During 2012, the amplitude of the diurnal evolutions of -𝑄^∗ varied from a maximum of 554 ± 14 W m^-2 in February to a minimum of 369±13 W m^-2 in July. On the other hand, -𝛥𝑄_𝑆 varied from a maximum of 249± 47 W m^-2 in April to a minimum of 181 ± 58 W m^-2 in July.

As observed previously by Ferreira et al.¹² and Oliveira et al.,¹⁷ 𝛥𝑄_𝑆 represents a significant fraction of 𝑄^∗, The seasonal variation of −𝛥𝑄_𝑆 in 2012 correspond to fraction of −𝑄^∗ of 56.1 % in April and 49.1% in July, indicating that during summer months the heat store in the suburban canopy of the megacity of São Paulo is slightly larger than in the winter months.

Seasonal and interannual variations of daily values and 𝑄^* fractions

The seasonal and interannual variations of monthly average daily values of H, LE and –𝑄^∗ observed during 2009, 2010 and 2012 in the PM IAG are indicated in the Figure 4. The seasonal variations of H and LE are close related to the one for 𝑄^∗, with maximum of 5 ± 0.5 MJ m^-2 day^-1 for H and 5.3 ± 0.6 MJ m^-2 day^-1 for LE in November (summer), and a minimum of 1.3 ± 0.2 MJ m^-2 day^-1 for H in June and 1.9 ± 0.2 MJ m^-2 day^-1 for LE in August (winter). In average, daily values of –𝑄^∗ show a maximum of 11.6 ± 1.1 MJ m^-2 day^-1 in March and a minimum of 4.5 ± 0.9 MJ m^-2 day^-1 in June. Daily values of H are systematically larger than LE during August-October 2012 in the suburban area of the megacity of São Paulo.

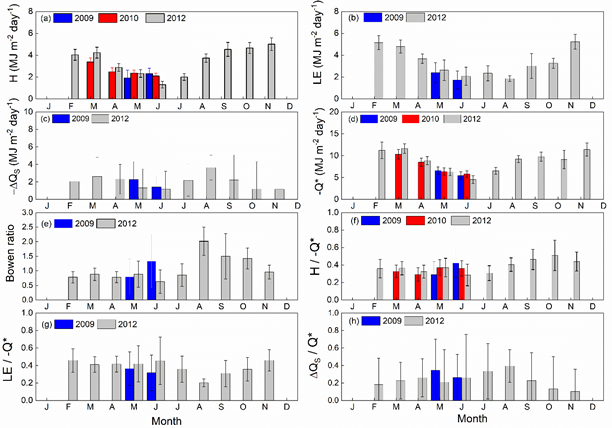
Figure 4 Seasonal variation of monthly average daily values of (a) H, (b) LE, (c) �ΔQs and (d) -Q*, (e) Bowen ratio; (f) H/-Q*; (g) LE/-Q* and (h) ΔQs/�Q* observed in the megacity of S�o Paulo from 2009 to 2012.

The temporal evolution of monthly average daily values of 𝐻 in 2010 and 𝐻 and 𝐿𝐸 in 2009 are alike 2012 (Figure 4). Comparatively, daily values of 𝐻 in May (June) 2009 are lower (higher) than in 2010 and 2012. In the other hand, monthly average daily values of LE in 2009 are lower than in 2012, during May and June. The major reason for the interannual variation between 2009 and 2012 is the differences in the footprint patterns between these years.

The seasonal and interannual variations of Bowen ratio (𝐻⁄𝐿𝐸), and net radiation fractions of sensible (𝐻/−𝑄^∗), latent (𝐿𝐸/−𝑄^∗) and store energy (∆𝑄_𝑠/𝑄^∗) fluxes, based on monthly averaged daily values of H, LE, −∆𝑄_𝑠 and −𝑄^∗, for 2009, 2010 and 2012, are also indicated in the Figure 4. During 2012, the Bowen ratio display a maximum of 2.0 ± 0.5 in August and a minimum of 0.63 ± 0.40 in June. From August to October the Bowen ratio remains above unity reflecting the fact that these months are the driest months of 2012 in the megacity of São Paulo. The seasonal variation of −𝑄^∗ fractions of H and LE are given by the seasonal variation of their daily values modulated by seasonal variation of −𝑄^∗.

Empirical modeling of diurnal evolution

The MPTM-OHM empirical models (Eqn. 5-7) are calibrated using hourly values of 𝐻, 𝐿𝐸, 𝑄^∗ and air temperature measured at PM IAG (Table 1) during May and June 2009, 2010, and 2012. It is assumed OHM-parameters that 𝑎₁ = 0.56, 𝑎₂ = 0.46 hours and 𝑎₃ = -37.75 W m^-2, as proposed by Ferreira et al.,¹² are valid to estimate ∆𝑄𝑠 (Eqn. 7) in a suburban area of São Paulo Megacity like PM IAG.

Figure 5 shows the diurnal evolution of observed (Obs) and modeled (Mod) monthly average hourly values of SEB components during calibrations months, obtained by trial-and-error as the best performance with = 10 W m^-2 and 𝛼^′ = 0.55 (1.0) for day (night) period. One criterion adopted in the trial-and-error procedure was to enforce H slightly higher than LE as an expected behavior of these SEB components in a suburban area and observed in the PM IAG (Sect. 3.1) and in other studies.^12,17 The diurnal evolutions of modeled SEB components display a phase among 𝑄^∗ and H, LE and ∆𝑄_𝑠 during all 6 months (Figure 3b, d, f, h). The absolute maximum of ∆𝑄_𝑠 occurs 1 hour before 𝑄^∗, whereas for 𝐻 and LE occurs 2 hours after 𝑄^∗.

Figure 5 Diurnal evolution of monthly average hourly values of Q*, ΔQs, H and LE observed (Obs) and modeled (Mod) in the megacisty of São Paulo during May and June in 2009, 2010 and 2012. In (e) and (g) observed LE is not available in 2010.

To evaluate the performance of empirical model, monthly average hourly values of observed and modeled H, LE and 𝛥𝑄_𝑠 from February to April and July and November of 2012 (data not used in the calibration) are objectively analyzed (Figure 6, Table 2). Figure 6 indicates the dispersion diagrams between observed and modeled hourly values of H, LE and 𝛥𝑄_𝑠. Table 2 displays the typical statistical parameters, Mean Bias Error (𝑀𝐵𝐸) and Root Means Square Error (𝑅𝑀𝑆𝐸), estimated according to the following expressions: 𝑀𝐵𝐸 = 1⁄𝑁 ∑^𝑁_𝑖=1(𝑂_𝑖 − 𝑀_𝑖) and RMSE $=\sqrt{1/N{\displaystyle {\sum }_{i=1}^N\left(O_i-M_i\right)2}}$ , where 𝑀_𝑖 and 𝑂_𝑖 are the modeled and observed values respectively and N is the total number of values.

Figure 6 Dispersion diagram between modeled and observed monthly average hourly values of (a) H, (b) LE and (c) ΔQs from February to April and July to November 2012 in the megacity of São Paulo. Dashed lines correspond to the main diagonal and solid red lines to the linear fit.

In general, the dispersion of these points around the linear fit curve are small, and the linear fitted curves are very close to the 1:1 diagonal (Figure 6). Positive values of 𝑀𝐵𝐸 indicated that model underestimates observations and vice versa. Small values of 𝑅𝑀𝑆𝐸, comparatively to the mean values of M_i and O_i, indicate model performs well (Table 2).

The model performance is excellent for monthly average hourly values of 𝐻 and ∆𝑄_𝑠, with correlation coefficient equal to 0.91 and 0.93, respectively (Table 2). The model underestimates 𝐻 (𝑀𝐵𝐸 > 0) and overestimates 𝐿𝐸 and ∆𝑄_𝑠 (𝑀𝐵𝐸 < 0). Values of 𝑅𝑀𝑆𝐸% ≤ 11.5% indicates that the empirical model MPTM-OHM performs well for monthly average hourly values of 𝐻, 𝐿𝐸 and ∆𝑄𝑠. It is interesting to note that the mean values of 𝐻 and 𝐿𝐸 display the largest discrepancies, while the maximum and minimum values show the smallest.

The surface-atmosphere interaction can be evaluated by the temporal and spatial description of SEB components, mainly 𝐻, 𝐿𝐸, 𝑄^∗ and ∆𝑄_𝑠. Knowing these SEB components in urban areas is important to understand the role of cities in the climate of urban areas and to objectively define actions to mitigate the adverse climate effects induced by urbanization. This knowledge is particularly important in Brazil where more than 85% of population leaves in urban areas.

In this work, the seasonal and interannual variations 𝐻, 𝐿𝐸, 𝑄^∗, and ∆𝑄_𝑠 are observationally characterize during 2009, 2010 and 2012 in a suburban area of the megacity of São Paulo, Brazil. This characterization is based on monthly average hourly values of 𝐻 and 𝐿𝐸, estimated by applying eddy-covariance method to turbulence measurements. Simultaneous measurements of 𝑄^∗, air temperature and wind speed, were used to estimate ∆𝑄_𝑠, as residual of the SEB equation, and perform a footprint analysis. Furthermore, monthly average hourly values of 𝐻, 𝐿𝐸 and ∆𝑄_𝑠, estimated during May and June 2009, 2010, and 2012, were applied to validate the empirical model MPTM-OHM to estimate monthly average hourly values of SEB components in a suburban area of the megacity of São Paulo, using monthly average hourly values of 𝑄^∗ and air temperature as input parameters.

The diurnal evolution of monthly average hourly values of 𝐻, 𝐿𝐸, 𝑄^∗ and 𝛥𝑄_𝑆 observed in 2012 indicate a seasonal variation with a daytime maximum with 𝐻 varying from a maximum of 180 ± 12 W m^-2 in October to a minimum of 80.1 ± 9 W m^-2 in June, 𝐿𝐸 varying from a maximum of 152.0 ± 7.6 W m^-2 in February to a minimum of 66.4 ± 7.6 W m^-2 in September, -𝑄^∗ varying from a maximum of 554 ± 14 W m^-2 in February to a minimum of (369±13) W m^-2 in July, and -𝛥𝑄_𝑆 varying from a maximum of (249± 47) W m^-2 in April to a minimum of 181 ± 58 W m^-2 in July.

The seasonal and interannual variations of monthly average daily values of H, LE and −𝑄^∗, and respective fractions (Bowen ratio, 𝐻/−𝑄^∗, 𝐿𝐸/−𝑄^∗,∆𝑄_𝑠/𝑄^∗) observed during 2009, 2010 and 2012 are consistent observed diurnal cycles of monthly average hourly values. The seasonal variations of H and LE are close related to the one for 𝑄^∗, with maximum H= 5 ± 0.5 MJ m^-2 day^-1 and LE = 5.3 ± 0.6 MJ m^-2 day^-1 in November (summer), and a minimum H =1.3 ± 0.2 MJ m^-2 day^-1 in June and LE = 1.9 ± 0.2 MJ m^-2 day^-1 in August (winter). In average, daily values of −𝑄^∗ show a maximum of 11.6 ± 1.1 MJ m^-2 day^-1 in March and a minimum of 4.5 ± 0.9 MJ m^-2 day^-1 in June. Daily values of H are systematically larger than LE during August-October 2012 in the suburban area of the megacity of São Paulo.

These observations indicated that 𝐻, 𝐿𝐸, 𝑄^∗ and 𝛥𝑄_𝑆 display seasonal and interannual variations consistent with typical features of local climate and land use of the suburban area of the megacity of São Paulo. During driest months (August-October) the amplitude of H is systematically larger than LE, with a Bowen ratio varying from a maximum of 2.0 ± 0.5 in August and a minimum of 0.63 ± 0.40 in June, because the vegetation fraction in the area investigated (PM IAG) is large enough to respond to the seasonal variation of moisture content of both lower-atmosphere and canopy-soil. As observed previously by Ferreira et al.¹², Rabelo³¹ and Oliveira et al.,¹⁷ 𝛥𝑄_𝑆 represents a significant fraction of 𝑄^∗, The seasonal variation of −𝛥𝑄_𝑆 in 2012 correspond to fraction of −𝑄^∗ of 56.1 % in April and 49.1% in July, indicating that during summer months the heat store in the suburban canopy of the megacity of São Paulo is slightly larger than in the winter months.

The MPTM-OHM empirical model was able to simulate the diurnal evolution of monthly average values of 𝐻 and 𝐿𝐸 in the suburban areas of the megacity of São Paulo considering as input the monthly average hourly values of 𝑄^∗ and air temperature and considering  = 10 W m^-2 and 𝛼^′ equal to 1.0 for nighttime period and 0.55 for daytime period.

The MCITY BRAZIL and BIOMASP+ projects were sponsored by the following Brazilian Research Foundations: FAPESP (2011/50178-5; 2020/07141-2), FAPERJ (E26/111.620/2011, E26/103.407/2012), and CNPq (309079/2013-6; 305357/2012-3, 462734/2014-5, 304786/2018-7). The first author acknowledges the scholarship provided by CAPES (001).

Conflicts of interest

The authors declare that they have no conflicts of interest.

1. Piringer M, Grimmond CSB, Joffre SM, et al. Investigating the Surface Energy Balance in Urban Areas – Recent Advances and Future Needs. Water Air and Soil Pollution: Focus. 2022;2:1–16.
2. Roth M, Jansson C, Velasco E. Multi-year energy balance and carbon dioxide fluxes over a residential neighborhood in a tropical city. Int J Climatol. 2017;37:2679– 2698.
3. Zhou Q. A Review of Sustainable Urban Drainage Systems Considering the Climate Change and Urbanization Impacts. Water. 2014;6(4):976–992.
4. IBGE. 2010.
5. Coutts AM, Beringer J, Tapper NJ. Impact of increasing urban density on local climate: spatial and temporal variations in the surface energy balance in Melbourne, Australia. J Appl Meteor Climatol. 2007;46:477–493.
6. Christen A, Vogt R. Energy and Radiation Balance of a Center European City. Int J Climatol. 2004;24:1395–1421.
7. Pigeon G, Legain D, Durand P, et al. Anthropogenic Heat Release in an Old European Agglomeration (Toulouse, France). Int J Climatol. 2007;27:1969–1981.
8. Sailor DJ, Lu L. A Top-Down Methodology for Developing Diurnal and Seasonal Anthropogenic Heating Profiles for Urban Areas. Atmos Environ. 2004;38(17):2737–2748.  
9. Ferreira MJ, Oliveira AP. Estudo do Balanço de Energia na Superficie de São Paulo. Novas Edições Acadêmicas. VDM Publishing House Ltd. Beau Bassin-Rose Hill, Mauritius, 2019. p. 176. ISBN: 978-613-9-66483-2.
10. Roberts SM, Oke TR, Grimmond CSB, et al. Comparison of Four Methods to Estimate Urban Heat Storage. J Appl Meteoro Climatol. 2006;45(12):1766–1781.  
11. Grimmond CSB, Cleugh HA, Oke TR. An objective heat storage model and its comparison with other schemes. Atmos. Environ. 1991;25(3):311–326.
12. Ferreira MJ. Oliveira AP, Soares J. Diurnal variation in stored energy flux in São Paulo city, Brazil. Urban Climate. 2013;5(107): 36–51.  
13. Yi C, Anderson D, Turnipseed A, et al. The Contribution of Advective fluxes to Net Ecosystem Exchange in a Highelevation, Subalpine Forest. Ecol Appl. 2008;18(6):1379–1390.
14. Stewart ID, Oke TR. Local Climate Zones for Urban Temperature Studies. Bull Am Meteorol Soc. 2012;93:12.
15. Ferreira MJ, Oliveira AP, Soares J. Anthropogenic heat in the City of São Paulo, Brazil. Theor Appl Climatol. 2010;104:43–56.
16. Ribeiro FND, Oliveira AP, Soares J, et al. Effect of sea breeze propagation on the urban boundary layer of the metropolitan region of Sao Paulo, Brazil. Atmospheric Research. 2018;214:174–188.
17. Oliveira AP, Marques Filho EP, Ferreira MJ. Assessing urban effects on the climate of metropolitan regions of Brazil - Preliminary results of the MCITY BRAZIL project. Exploratory Environmental Science Research. 2020;1(1):38–77.
18. Olivera AP. Personal Communication. 2023.
19. Silveira LC, Oliveira AP, Sánchez MP, et al. Observational Investigation of the Statistical Properties of Surface-Layer Turbulence in a Suburban Area of São Paulo, Brazil: Objective Analysis of Scaling-Parameter Accuracy and Uncertainties. Bound Layer Meteorol. 2022;185:161–195.
20. Weber S, Kordowski K. Comparison of atmospheric turbulence characteristics and turbulent fluxes from two urban sites in Essen, Germany. Theor Appl Climatol. 2010;102:61–74.
21. Quan L, Hu F. Relationship between turbulent flux and variance in the urban canopy. Meteorol Atmos Phys. 2009;104:29–36.
22. Aubinet, M, Vesala T, Papale D. Eddy Covariance: A Practical Guide to Measurement and Data Analysis. Springer Dordrecht Heidelberg London New York.  2012.
23. Kljun N, Calanca P, Rotach MW, et al. A simple two–dimensional parameterization for Flux Footprint Prediction (FFP). Geosci Model Dev. 2015;8(11):3695–3713.
24. Priestley CHB, Taylor RJ. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon Wea Rev. 1972;100(2):81–92.
25. Camuffo D, Bernardi A. An observational study of heat fluxes and the relationship with net radiation. Bound Layer Meteorol. 1982;23:359–368.
26. De Bruin HAR, Holtslag AAM. A simple parameterization of the surface fluxes of sensible and latent heat during daytime compared with the Penman-Monteith concept. J Appl Meteorol. 1982;21(11):1610–1621.
27. De Bruin HAR. A model for the Priestley-Taylor parameter 𝛼. J Clim Appl Meteorol. 1983;22:572–578.
28. Hanna SR, Chang JC. Boundary-Layer parameterizations for applied dispersion modeling over urban areas. Bound-Layer Meteorol. 1992;58:229–259.
29. Grimmond CSP, Oke TR. Turbulent Heat Fluxes in Urban Areas: Observations and a Local-Scale Urban Meteorological Parameterization Scheme (LUMPS). J Appl Meteorol. 2002;41(7):792–810.
30. Anandakumar K. A Study on the Partition of Net Radiation into Energy Fluxes on a Dry Asphalt Surface. Atmos Environ. 1999;33(24-25):3911–3918.
31. Rabelo FD. Observational investigation of the turbulent fluxes of sensible and latent heat at the surface in the Metropolitan Region of São Paulo City. Master thesis. Department of Atmospheric Sciences. Institute of Astronomy, Geophysics and Atmospheric Sciences. University of São Paulo. São Paulo. SP. Brazil. (In Portuguese).