This study examines the comprehensive precipitation trend and temperature trends across six locations in southern Nigeria using 1971 to 2010 monthly data obtained from the Nigeria meteorological agency (NIMET). Spatio-temporal variation of monthly rainfall was examined across the region. Non-parametric Mann Kendall method was used to investigate the monthly, seasonal and annual rainfall and temperature trends across this region. The analysis of rainfall revealed a most significant increasing trend in most of the locations with few decreasing trends. Likewise, a significant increasing trend was observed in temperature indicators. Decadal wise percentage of rainfall with the occurrence of the deficit and excess rainfall years were also examined. Rainfall was forecast till the year 2050 using Fourier analysis method. The result showed the increasing trend rate of rainfall oscillating between 0.046mm/year and 0.29mm/year in this region. This suggests increasing expected flood in southern Nigeria.

Keywords: decadal, flood, Fourier, Kendall, oscillation, precipitation 

Climate is a function of a region’s weather over a period of time and depends on latitude and the geographical location of a place. Climate change is a vital factor that determines the environmental, social and economic issue. Climate change is a global occurrence and is a function of latitude, terrain, altitude and water system which cause it to vary from one place to another.¹ IPCC,² Reported that the Sub-Saharan region of Africa is highly prone to climate change.³ According to IPCC,² Climate change influenced the distribution of the world’s rainfall to fluctuate which lead to more chaotic weather around the world. Undoubtedly, the world is presently under the threat of climate change problems like global warming, greenhouse gas effects, flooding, acid rain typhoons, rising sea levels, rising sea temperatures resulting in depletion of marine organisms, earthquakes, windstorms, land and mudslides, desertification, tsunami, erosion, volcanic activities, hurricanes, pollution, deforestation among several others. This was attributed to an increase in the average global temperature. Climate change is principally a major problem caused by the increase in anthropology activities leading to several direct and indirect impacts on health.⁴ Amount of moisture circulating in the atmosphere increases as evaporation rates, which is associated with tropospheric warmth increases. This contributes to more humidity and intense precipitation that trigger more flooding over land.⁵ Many resources which include air, water, soil, minerals, metals, energy, plants, and animals needed by Humans being are anchored on Earth’s land, ocean, atmosphere, and biosphere. As the global human population increases and people’s demands for better living conditions increase, resources considered readily available in the past, such as land for agriculture or drinkable water, are becoming scarcer and more valued. It threatens the achievement of the Millennium Development Goals aimed at poverty and hunger reduction, health improvement and environmental sustainability.⁶ This factor is highly necessary for Africa, where the majority depend on agriculture. The impact of climate change on crop yields is, therefore, a major concern in this region.

In southern Nigeria, climate change is also reflected in the massive flood experienced in 2012, where houses, farms, farm products, properties, and even human beings were swept away. Akukwe et al.,⁷ Recorded various locations across Nigeria that have an incident of a devastating flood. The rainfall is changing on both the global and the regional scales.^3,8‒13 Water resources of a region such as a streamflow, soil moisture, and groundwater are influence of changes in hydrological factors which anchor majorly on precipitations. This work covers six stations across the southern region of Nigeria as shown in Figure 1. This region is tropical humid characterized by long wet season (April-October) and a short dry season (November-March). The climate of southern Nigeria is regulated by the influence of the Tropical Maritime (mT) air mass, and the Tropical Continental (cT) air mass. The mT air mass originates from the southern high-pressure belt located off the Namibian Coast. The mT and cT air masses converge at a place called the Inter Tropical Discontinuity (ITD). The seasonal northward and southward migration of the ITD dictates the weather pattern of Nigeria.¹⁴ Average rainfall in this region is between 1524 mm and 2032 mm.

Figure 1 Southern Nigeria showing study locations.

Forty years monthly rainfall (mm), maximum temperature, minimum temperature (degree Celsius) across the six stations in Southern Nigeria from 1971 to 2010 were collected from the Nigerian Meteorological Agency (NIMET) archive. Monthly and seasonal variation of rainfall were constructed the obtained data. Statistical features of precipitation were examined across the region.

Data analysis

Kendall’s test which was first adopted by Hirsc et al.,^15,16 and modified by Mann-Kendall analysis^17,18 is normally used to detect rainfall and temperature trend. This analysis can handle normality, seasonal data and it also has high asymptotic efficiency Fu et al.¹⁹ Fu et al.,²⁰ Kendall test was applied on monthly, seasonal and annual rainfall and temperature data at a particular station to estimate Kendall statistic, Z using.^18,20,21

                                              $Z=\{\begin{array}{c}\frac{s-1}{{\left[Var\left(s\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}ifs>0\\ 0ifs=0\\ \frac{s+1}{{\left[Var\left(s\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}ifs<0\end{array}$                                                                                     (1)

where

$\mathrm{ V}ar\left(s\right)=\frac{\left[n\left(n-1\right)\left(2n+5\right)-{\displaystyle \sum _{t}t\left(t-1\right)\left(2t+5\right)}\right]}{18}$                                                                                            (2)

$\mathrm{ s}={\displaystyle \sum _{k=1}^{n-1}{\displaystyle \sum _{j=k+1}^n\mathrm{sgn}\left(x_j-x_k\right)}}$                                                                                                                                                                                            (3)

$\mathrm{ s}ign(y)=\{\begin{array}{c}1ify>0\\ 0ify=0\\ -1ify<0\end{array}$                                                                                                                                                                                                                       (4)

Where x is a variable, a sample n independent and identically distributed random variables (monthly rainfall or temperature). A positive or negative Z represents an upward or downward trend respectively. The linear rate of change is determined from Sen’s slope. The magnitude of the trend is estimated using the Sen’s slope estimator^22,23 A positive value of β denote increasing value with time (an upward trend), where a negative value of β represents a downward trend Asfaw et al.,²⁴ Fu et al.²⁰

 Sen’s slope estimation is

$\mathrm{ \beta }=\frac{x_{jk}-x_{ik}}{j-i}$ k=1,2,…q                                                                                                                       (5)

Where x_jk and x_ik are considered as data values at time j and i is the media over all possible combinations of pairs from the month for the entire dataset.

Fourier series

Fourier model was developed to predict and forecast rainfall till 2050. Monthly rainfall, y(t) were generated using:

$\mathrm{ y}\left(t\right)=a_o+{\displaystyle \sum _{i=1}^{\infty }\left(a_n\cos nwt+b_n\sin nwt\right)}$                                                                                                                                                                                            (6)

Where a_o is constant, a_n and b_n are amplitude constant, n is an integer (1<n<∞).

Seasonal distribution of rainfall in southern Nigeria

In Figure 2 the value of rainfall across this region has represented was higher in the rainy months of April-October. Two peaks were discernible during this period (July and September). These peaks concise with the peak of stratiform and convective rainfall respectively. The dip in between noticed in August during which short period of the dry season normally experienced in southern Nigeria (also known as August break). During this period, intertropical discontinuity reaches its peak in the north before it starts to migrate southward. Southern Nigeria. Table 1A–Table 1F show some characteristics of precipitation across the six locations during various decades. The maximum mean value of 131.6, 119.2, 114.4 and 195.8 was observed in Lagos, Ibadan, Osogbo and Benin respectively during the fourth decade of 2001-2010. In Port Harcourt and Calabar, maximum, mean values of 194.0 and 251.4 respectively, were observed during the third decade of 1991-2000. The variation between the fourth decadal mean and median across the locations depict that the precipitation across this region in Nigeria has experienced a lot of up and down during this period. The values of upper quartile (Q₁) and lower quartile (Q₁) indicate oscillation of rainfall during this period in the entire region. High coefficient of variation noticed across all the locations depicts daily instability and oscillation of rainfall during the decade. Positive and negative skewness and kurtosis were observed during different decades across the locations.

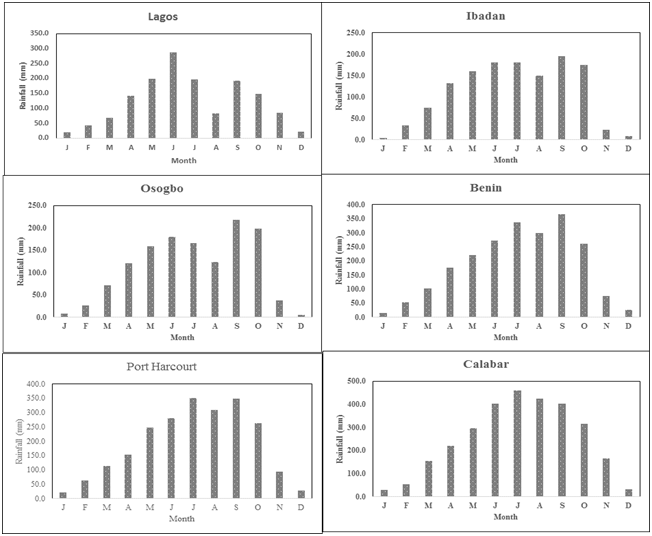
Figure 2 The spatial and temporal variations of mean monthly rainfall in the various stations across.

The non-parametric trend of long-term meteorological indicators

Result on monthly, seasonal and annual basis for the three meteorological indicators with a significant trend across the six stations in southern Nigeria is presented in Figure 3A-Figure 3C. These analyze are constructed in the time period 1971 to 2010. The first two bars in each month, season, and annual represent temperature indicators, while the remaining one depicts precipitation indicator. The results of the Mann Kendall test for monthly maximum temperature data revealed a statistically significant increasing trend for most of the month (at less than 0.1 significant levels) across the stations. A statistically significant trend was observed across all the months, season and annual in Lagos except in April and October where a non-significant increasing trend was observed. A similar trend was observed in other locations with a non-significant increasing trend in February, April, and May (Ibadan), March–October (Osogbo), April, May, and August (Benin), April (Port Harcourt) and March, April, and November (Calabar). The monthly minimum temperature experienced statistically significant positive trend across all the months, seasons and on an annual scale in Lagos and Ibadan (at less than or equal to 0.1 significant levels). Significant trend was observed also in Benin across all the months except in January and February. Temperature minimum is statistically significant in May, July, August, and September in Osogbo. A similar trend was observed in Port Harcourt and Calaba. The result of MK on monthly rainfall dataset revealed both increasing and decreasing order across all the stations in this region. The data experienced a statistically significant increasing trend in June, October, and November and annually in Lagos. Also in Ibadan, the statistically significant increasing trend was noticed in September, October, wet season and on an annual scale. Rainfall trend is also significant in July, wet season and on annual in Osogbo. A statistically significant decreasing trend was observed in the dry season in Port Harcourt. In Calabar, rainfall experienced statistically significant positive trend in November and dry season.

Figure 4 depicts the empirical and theoretical cumulative distribution function (CDF) for long-term seasonal rainfall (dry and wet) across the six locations. Both empirical and theoretical CDF for both dry and wet season is reasonably close and are more discernable. Table 2 shows the CDF mean (µ) and standard deviation (σ) with their error (µ_se and σ_se respectively). Highest CDF mean of 359.70 with the lowest value of 166.25 was obtained at Calabar and Osogbo respectively during the wet season. Whereas, during the dry season the highest and lowest mean of 86.14 and 28.33 respectively, were obtained in Calabar and Ibadan. The highest deviation of 51.77 and 30.05 was noticed in Calabar during the wet and dry season respectively.

Figure 3A Mann-Kendall trend test result of rainfall in Lagos and Ibadan (1971-2010).

Figure 3B Mann-Kendall trend test result of rainfall in Osogbo and Benin (1971-2010).

Figure 3C Mann-Kendall trend test result of rainfall in Port Harcourt and Calabar (1971-2010).

Figure 4 Cumulative distribution of long-term rainfall in southern Nigeria.

Decadal wise distribution of seasonal rainfall

The number of excesses and deficit rainfall years with decadal-wise departure from normal are presented in Table 3. The number of years the rainfall is less or more than the standard deviation is known as excess or deficient rainfall years respectively. Krishnakuma et al.,²⁵ During the dry decadal 1971 -1980, the highest three excess rainfall years were observed at Port Harcourt with one deficit years and was noticed in each location during this period except Ibadan. The highest value of three excess rainfall years was observed at Lagos and deficit of one on each location except Osogbo and Benin where two deficit rainfall years are recorded. Similarly, two excess rainfall years were observed across the locations, in the dry decade 1981–1990. The highest value of this deficit rainfall year was observed in Calabar during this period. In 1991-2000 and 2001-2010, values of excess rainfall years and deficit rainfall years oscillate between one and three during wet and dry except in Benin where three excess rainfall years were noticed during the wet season. In the dry period of 1971 to 2010, there were eight, seven, six, six, eight and six excess rainfall years and six, six, six, five, seven and seven deficit rainfall years across Lagos, Ibadan, Osogbo, Benin, Port Harcourt, and Calabar respectively. Likewise, during the wet season, the excess rainfall years are 9, 6, 6, 8, 6, 7 and deficit years are 7, 7, 8, 9, 6, 8 respectively. On an annual basis, in Lagos, excess and deficit fluctuate between zero and one whereas, in another location, it oscillates between one and two except Ibadan where we have a deficit of three in 1981-1990 decade.

Rainfall prediction and forecast in southern Nigeria

Rainfall data were well fitted by the Fourier trend model (Figure 5). The result of annual and predict rainfall show overestimation annual rate of 0.38mm/year, 0.35mm/year, 0.34mm/year and 0.58mm/year in Lagos, Ibadan, Osogbo and Calabar respectively. Underestimation, annual rainfall rate of 0.48 mm/year and 0.027 mm/year were noticed in Benin and Port Harcourt respectively. Rainfall was forecasted across the locations till 2050. Forecasted annual rainfall rate across the location show increasing trend at a rate of 0.046mm/year, 0.045 mm/year, 0.29mm/year, 0.18mm/year and 0.18 mm/year in Lagos, Ibadan, Benin, Port Harcourt, and Calabar respectively. However, the result at Osogbo shows the decreasing trend at a rate of 0.058mm/year annually. This will likely contribute to increase in flooding in more of the southern locations in Nigeria.

Figure 5 Annual actual, predicted and forecast rainfall distribution in southern Nigeria.

Using long-term monthly rainfall and temperature data which spanned between 1971 and 2010, seasonal variation of rainfall, non-parametric trend using Mann Kendall and decadal distribution of rainfall were examined across six locations in southern Nigeria. The highest values of rainfall were noticed in July in all the locations. Significant increasing trends were observed in most of the monthly and seasonal temperature in most of the locations. Rainfall trend across this region oscillate between positive and negative trend. The average decadal rainfall in this region fluctuates between 100 mm/year and 255mm/year. Empirical and theoretical cumulative distribution function (CDF) for long-term seasonal rainfall (dry and wet) across the six locations was examined. During the wet season, maximum CDF mean value of 359 with a minimum value of 166 was obtained in Calabar and Osogbo respectively. Fourier method was used to predict and forecast monthly rainfall. Overestimation rate of range 0.35-0.58mm/year was observed in five of the locations. Whereas underestimation rate was observed in Osogbo. Forecast result showed increasing rate ranges between 0.045 mm/year and 0.290 mm /year across the five locations, except Osogbo. With this result, the flood is except in most of the locations across southern Nigeria.

We thank the Nigeria Meteorological Agency (NIMET) for making their data available for this work.

The author declares that there is no conflict of interest.

1. Beldring S, Engen‒Skaugen T, Førland E, et al. Climate change impacts on hydrological processes in Norway based on two methods for transferring regional climate model results to meteorological station sites. Tellus A – Dynam Meteorol Oceanograph. 2008;60(3):439‒450.
2. IPCC Intergovernmental Panel on Climate change. IPCC Secretariat (2011) America’s climate choices. The National Academies Press, Washington D.C 15. 2011.
3. Bekele B, Alamirew T, Kebede A, et al. Analysis of rainfall trend and variability for agricultural water management in Awash River Basin, Ethiopia. Journal of Water and Climate Change. 2016;8(1):127‒141.
4. Loo YY, Billa L, Singh A. Effect of climate change on seasonal monsoon in Asia and its impact on the variability of monsoon rainfall in Southeast Asia. Geosci Frontiers. 2015;6(6):817‒823.
5. Held IM, Soden BJ. Robust Responses of the Hydrological Cycle to Global Warming. J Climate. 2006;19:5686–5699.
6. WWAP (United Nations World Water Assessment Programme). The United Nations. 2015.
7. Akukwe TI, Krhoda GO, Oluoko‒Odingo AA. Principal component analysis of the effects of flooding on food security in agrarian communities of southeastern Nigeria. Int J Hydro. 2018;2(2):205‒212.
8. Takahashi HG, Yasunari T. Decreasing Trend in Rainfall over Indochina during the Late Summer Monsoon: Impact of Tropical Cyclones Frontier Research Center for Global Change (FRCGC). Journal of the Meteorological Society of Japan. 2008;86(3):429–438.
9. Rodrıguez‒Puebla C, Encinas AH, Nieto S, et al. Spatial and temporal patterns of annual precipitation variability over the Iberian Peninsula. International Journal of Climatology. 1988;18(3):299–316.
10. Gemmer M, Becker S, Jiang T. Observed monthly precipitation trends in China 1951–2002. Theoretical and Applied Climatology. 2004;77(1‒2):39–45.
11. Kayano MT, Sans´ıgolo C. Inter annual to decadal variations of precipitation and daily maximum and daily minimum temperatures in southern Brazil. Theoretical and Applied Climatology. 2008;97(1‒2):81–90.
12. Fukutomi Y, Yasunari T. 10‒25 day intraseasonal variations of convection and circulation over East Asia and western north pacific during early summer. J Meteor Soc Japan. 1999;77(3):753–769.
13. Weng H, Lau KM, Xue Y. Multi‒scale summer rainfall variability over China and its long‒term link to global sea surface temperature variability. Journal of the Meteorological Society of Japan. 1999;77(4):845‒857.
14. Amadi SO, Udo SO, Ewona IO. Trends in Monthly Mean Minimum and Maximum Temperature Data over Nigeria for the Period 1950‒2012. International Research Journal of Pure and Applied Physics. 2014;2(4):1‒27.
15. Hirsch RM, Slack JR, Smith RA. Techniques of trend analysis for monthly Water quality data. Water Resour Res. 1982;18(1):107–121.
16. Dashkhuu D, Kim JP, Chun JA, et al. Long‒term trends in daily temperature extremes over Mongolia. Weather Clim Extrem. 2014;56:26–33.
17. Kendall MG. Rank Correlation Methods, 4th Edition. Charles Griffin: London. 1975.
18. Gan TY. Hydroclimatic Trends and Possible Climatic Warming in the Canadian Prairies. Water Resources Research. 1998;34(11):3009‒3015.
19. Fu GB, Chen SL, Liu CM, et al. Hydro‒Climatic Trends of the Yellow River Basin for the Last 50 Years. Climatic Changes. 2004;6(1‒2):49‒178.
20. Fu G, Yu J, Yu X, et al. Temporal variation of extreme rainfall events in China, 1961‒2009. Journal of Hydrology. 2013;487:48‒59.
21. Bouchard E, Qi Z. Long‒term trends of climate change and its impact on crop growing season on Montreal Island. Journal of Water and Climate Change. 2017;8(1):78‒88.
22. Theil H. A rank‒invariant method of linear and polynomial analysis, part 3. Nederlandse Akademie van Wettenschappen. Proceedings 1950;53:1397–1412.
23. Sen PK. Estimates of the regression coefficient based on Kendall's tau. J Am Stat Assoc. 1968;63(32):1379–1389.
24. Asfaw A, Simane B, Hassen B, et al. Variability and time series trend analysis of rainfall and temperature in north‒central Ethiopia: A case study in Woleka sub‒basin. Weather and Climate Extremes. 2017;19:29‒41.
25. Krishnakumar KN, Prasada Rao GSLHV, Gopakumar CS. Rainfall trends in twentieth‒century over Kerala, India. Atmos Environ. 2009;43(11):1940–1944.
26. World Water Development Report 2015. Water for a Sustainable World. Paris: UNESCO. 2015.