Analyses the thermal and Physico-mechanical properties of permafrost, received a convenient formula for calculating them with the economic development of the territory the spread of everfrozen soils.

Keywords: strength, deformation, durability, creep, destruction

A huge amount of water. At negative temperatures it smerzaetsja with the containing soil, forming a special Rock-"permafrost", possessing specific thermal and physic-mechanical properties. Permafrost occupies a vast space-not less than 25% of the total land area. It serves as the foundation of buildings and sooruzhenij, a container of minerals, the habitat of animals and plants. Therefore, the study of the properties of permafrost is the primary prerequisite for successful management in the area of dissemination

In solid state physics, a kinetic (thermofluctuation) concept of strength has been developed, the essence of which is contained in the formula for durability t_дл.¹

 $t_{дл}=t_{о}ехр[(U_o-gР)/RT]$    (1)

where U_o»Q_c- activation energy of destruction; Q_c- latent heat of sublimation; t_о»10^-13sec - the period of thermal oscillations of atoms; RT is the average energy of atomic vibrations; T is the temperature (K); P - pressure (strength); R is the universal gas constant; g is a coefficient that has the meaning of the volume of an atom at the time of sublimation. Formula (1) is based on the idea of the local nature of the destruction of interatomic bonds, in terms of microcracks and other structural defects that serve as stress concentrators. It is obtained as a result of the generalization of numerous tensile tests of various materials, including composite and heterogeneous. It should be noted that it can also be derived analytically, based on energy - entropy considerations.² From the formula (1) it follows that the durability is the final value, at P=0 it reaches its maximum, equal to t_о^.ехр(U_o/RT). I.e. the body is destroyed also in the absence of external pressure, under the action of time, which is the same active force of destruction as pressure and temperature. In,^2‒4 the limitation of formula (1) is shown, its applicability mainly for materials with high melting points and at high pressures. It is hypothesized that there are two mechanisms (types) for the destruction of a solid: near the melting point, brittle (“sublimation”), which implies the breaking of interatomic bonds (U_o»Q_c) and away from it, plastic (“smelting”), which implies dilution (U_o»Q_пл). Frozen soils are destroyed mainly according to the second type.

This article develops theoretical concepts of permafrost studies in terms of the staging of soil moisture crystallization, the connections of the strength and durability of frozen soils with phase transition temperatures, with global factors and time. Much attention has been paid to an insufficiently studied phenomenon - the supercooling of the freezing soil, during which, under certain conditions, the entire temperature spectrum of its future frozen state is recorded. This opens up great opportunities for early prediction of the strain state of frozen soil and cost savings for the production of expensive field tests of frozen soils.

The main stages of soil moisture crystallization are shown in Figure1. The formation of the structure of ice starts when its temperature drops below +4°C, when the density of water begins to slowly decrease, rushing to the density of ice. Bulk crystallization of water in time is preceded by its supercooling (metastable state) below the crystallization temperature t_кр to the value of t_пер (hidden, zero stage in Figure 1). Supercooling creates a temperature difference t_кр-t_пер, which is necessary for obtaining the energy of formation of the bulk crystallization front (interface of phases). After reaching t_пер the temperature of the soil rises abruptly to t_кр, and the first ice crystals, centers of the subsequent bulk (clear) crystallization, including two stages (1 and 2 in Figure 1), appear “into the light”. On the first one, at a constant temperature t_кр, free water freezes, on the second - loosely bound water. The temperature of the soil before the crystallization of its moisture (when t> t_кр) depends on the temperature of the coolant t_ох and its thermo-physical properties, according to the Fourier thermal conductivity law. With its start, this dependence is blocked by the latent heat of phase transitions Q_ф, when the heat capacity of the moist soil becomes an effective value.⁵

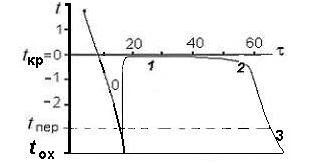
Figure 1 Stages of liquid transition to the solid phase (0, supercooling; 1, 2, crystallization of free (1) and bound (2) water; 3, cooling of frozen soil; τ, current time, min; t, current temperature, °C; t_кр, crystallization temperature; t_пер, supercooling temperature; t_ох,- cooler temperature (temperature in the permafrost chamber).

 ${С}_{эф}{}_{}={С}_{у}{}^{.}{\rho }_{ск}+{(d{W}_{н}/dt)}^{.}{Q}_{ф}{\rho }_{ск}$    (2)

where С_у, kJ/kg degree - specific heat capacity of the freezing soil; Q_ф=334kJ/kg is the latent heat of crystallization of soil moisture; W_н -moisture due to unfrozen water; ρ_ск- density of the dry soil unit. The second component in (2) is hundreds of times larger than the first. Under these conditions, the crystallization front becomes a screen (“zero curtain”), protecting the freezing soil from external cooling and ensuring the constancy of t_кр at the ^1st stage. At the 2^nd stage, water freezes in a certain range of temperatures. Here, each t_кр corresponds to a certain, gradually decreasing amount of unfrozen water and, accordingly, increasing deformation. At the end of the stage, at a sufficiently low temperature of the cooler t_ох, a hard-frozen state is established, characterized by a temperature t_тм≈t_пер≥t_ох, at which practically all bound water freezes. From Figure 1 it follows that, in general, with each temperature, when the thawed soil is cooled (on the left curve), it is possible to compare the temperature of the frozen soil (on the right curve) equal to it, which determines its strain state, including strength and other physical and mechanical properties. That is, during the supercooling of thawed soil, all temperatures are consistently demonstrated, which are then repeated at the 2-stage crystallization. In the reverse process, the transition of the solid phase to a liquid, metastable state is not realized. It is not necessary because there is unfrozen water in frozen soil at almost any temperature, and the phase interface is always present.

The lower the t_пер, the shorter the formation time of the crystallization front, or, which is the same, the smaller the supercooling period t_пер. At sufficiently low t_ох, the value of t_пер becomes less than the resolution of the measuring instruments and the entire supercooling section is not recorded by observations because of its smallness. For an example the Table 1 shows the results of experiments to determine t_кр and t_пер in peated clay soils with different t_ох.^3,4 From Table 1 we can see that t_пер is always higher than t_ох, and with decreasing t_ох, the supercooling area decreases and at t_ох around minus 6... 8°C goes beyond the limits of “visibility” of the devices.

Detailed studies of the dependence of t_пер on τ_пер were performed by S.E. Grechishchev et al.⁶ Approximation of this dependence gives.²

 $t_{пер}/t_{min}={({\tau }_{пер}/{\tau }_{min})}^g$    (3)

Where t_min and τ_min - the minimum temperature and period of supercooling in the experiment, g≈0.09 is the relative change in the volume of water during freezing. With the help of (3), it is possible to establish the minimum cooling temperature t_ох, at which the value of t_пер is still observed. Let us accept the conditions of one of the experiments:⁶ loam with moisture of 26, 2%, t_кр=-0.4... - 0.5°C, g»0,1; t_min=-3,3^оС and τ_min=30s. According to the calculation with the formula (3): at t_пер=-4,6^о, the value of τ _пер= 1s, at-5°, it is equal to 0.43s, and at -8°, it is just 0.004s. It is clear that in this case, t_пер is fixed at t_ох not lower than -5^оС. If t_ох is lower than the temperature of the solid-permeable state of the soil t_тм (in loams t_тm≈-6...-8^оС), supercooling is not observed, the first crystallization stage begins.

S.E. Grechishchev accepts that t_пер=t_ох. Although this equation is not observed in experiments, this assertion can be accepted if we assume an instantaneous change in temperature from t_пер to t_ох
and back, as shown in Figure 1. With an increase in t_пер, the duration of supercooling t_пер increases. As the temperature of the cooler approaches t_кр, the value of t_пер tends to an infinitely large value. The magnitude of supercooling — its temperature and duration — can be reduced and even nullified by shaking the sample, increasing the external pressure, lowering the temperature in the chamber, using various crystallization inocula. The value of g in (3) is close to the relative crystallization strain g » j_кр » 0,091, and the maximum supercooling (instantaneous, with the duration of supercooling equal to the period of atomic oscillations: t_пер=t _min=t _о»10^-13 sec) when substituted into the formula (3) experimental data are obtained equal to minus 22-24^оС. This is close to the minimum temperature at which ordinary water may still exist (not freeze).⁷ i.e. the extremes of the temperature of supercooling and crystallization are the same: about 0 and -22^оС.

The supercooling temperature, like the crystallization temperature, depends on the pressure. But if the crystallization temperature decreases with increasing pressure, then, as experimentally established,² the supercooling temperature, on the contrary, increases. This is evident from the Figure 2 shown for example: at P=0.1MPa, t_пер=-3.1°C; at P=5.7MPa, t_пер=-1.4°C.²

Figure 2 The temperature change of the freezing loam at P=0.1MPa (а) and P=5.7MPa (б).

Pressure, temperature and volumetric deformation characterizing the phase transformations of soil moisture are the main parameters of the state of frozen soils. The relationship between them in the limiting equilibrium state is governed by the Clapeyron-Clausius law, which we write in the following form.^2,5

 $dT/T=dP(V_{тв}-V_{ж})/Q_{ф}$    (4)

where T (K) is the temperature in Kelvins; Т_о=273(K) is the crystallization temperature at atmospheric pressure; Р-external pressure, kg/cm²; V_тв и V_ж - the specific volume of the solid and liquid phases; Q_ф is the latent heat of ice-water phase transitions, kJ/kg.

Integrating this equation gives:

_, $ln\left(T_o/T\right)=P(V_{тв}-V_{ж})/Q_{ф}$    (5)

With T/T_o» 0.9... 1, which is typical for frozen soils existing in the temperature range 0... -22^оС (273... 251К), replacement is possible

 $ln\left(T/T_o\right)\approx \left(T/T_o\right)-1=-t/T_o$    (6)

Then the equation of phase equilibrium is linearized:

 $t_{ф}=t_{кр}=Р(V_{тв}-V_{ж})T_o/Q_{ф}=Рj_{кр}{T}_o/L_{кр}=Рb$    (7)

Where t_ф=|Т-Т_о| - freezing point of water in ^оС with a plus sign; j_кр=(V_тв-V_ж)/V_ж = 0.091 is the relative crystallization strain; L_кр=Q_ф/V_ж - volumetric heat of crystallization, kJ/m³; b=(V_тв-V_ж)T_o/Q_ф, ^оС// MPa.

The coefficient b depends little on temperature, rising as it decreases, in different soils from about 0.08 to 0.14 ^oC/ MPa; on average, b»0.1^oC/MPa.^2,5 When describing melting, instead of j_кр and L_кр, relative deformation and volumetric heat of melting j_пл=(V_тв-V_ж)/V_тв=0.083 and L_пл=Q_ф/V_тв., L_кр<L_пл, а j_кр>j_пл are substituted into (10) by about 9%.. This difference is often neglected. From formula (10), at a known temperature, the pressure of phase transformations (pore pressure) is determined: Р_ф=t/b, positive during crystallization of water, resulting from the impossibility of free expansion, and negative during ice melting, resulting from the free release of pore volume. The index “ф” for t and P is set when they are functions of, respectively, P and t. Unlike most other substances, water during freezing increases in volume, and the temperature (in the range of 0 ÷ - 22^оС) and the pressure of phase equilibrium are not in direct, but in inverse connection. At about t = –22^оС and P ≈ 220 MPa.^2,7 the sign of the dependence of t_ф on P changes to the opposite: the value of t_ф begins to increase. At t <–22^оС ordinary water, and at P> 220 MPa, ordinary ice (ice I) does not exist (Figure 3).

Figure 3Area of existence of ordinary water at t <0оС.

The temperature and pressure at this limit, by analogy with supersaturated solutions of alloys are called eutectic (from Greek - fusible): t_эв ≈ –22^oC, Р_эв≈220MPa, since water at these indicators is in equilibrium with two solid phases - ice 1 and ice 3,⁷ i.e. falls under the definition of eutectic. The analysis of the actual material also showed that the spatial, mechanical, thermal and temporal parameters characterizing the boundaries of the existence of a solid phase of water are approximately similar:

 $1–(V_{ж}/V_{тв})=1–({Т}_{эв}/{Т}_{о})=Q_{пл}/Q_{с}=1-({Р}_{эв}{}_{.пл}/{Р}_{эв}{}_{.кр})»j_{пл}»0,083=1/12$    (8)

 $(V_{тв}/V_{ж})–1=({Т}_{о}/{Т}_{эв})–1=(Q_{с}/Q_{и})–1=({Р}_{эв}{}_{.кр}/{Р}_{эв}{}_{.пл})–1»j_{кр}»0,091=1/11$    (9)

Where Q_и and Q_c - latent heat of evaporation of water and ice sublimation (at t = -22^oC Q_c=2830kJ/kg, Q_и=Q_c– Q_пл=2830–235=2595kJ/kg); Р_эв.пл»216MPa and Р_эв.кр=235MPa - eutectic melting and crystallization pressures (power equivalents L_пл and L_кр at t = t_эв=-22^oC). From equations (11) - (12), the linearity of the distribution of t, P and j between their extreme values and an approximate analogy of the sum-total of these equations to gas laws follows. The similarity criteria in the equations are equal to the relative deformations of ice melting and water crystallization, and their reciprocal values coincide with the number of months in the earth and lunar annual cycles, which apparently indicates a relationship between the water-ice phase transitions and planetary factors.

Let us assume that changes in durability and the work of destruction (melting) of frozen soil, related to their maxima, are proportional to:

 $\Delta РV_{тв}/[{Р}_m(V_{тв}-V{\prime }_{ж})]=\Delta Рj_{пл}=\Delta \tau /\tau$    (10)

Where V′_ж, increasing content of unfrozen water in thawing soil.

Replacing Δτ and ΔР with differentials, we rewrite (13) in integral form,⁴ after integrating and simple transformation of which, we get:

 ${(t_{э}/t_{д})}^j{}^{пл} =(Р/{Р}_m)=Рb/t_{ф}$    (11)

where P is the pressure on the frozen body; Р_m - the maximum pressure that this body can withstand without breaking down during elementary time, determined from equation (10); te t_э is the minimum (elementary) time interval adopted in this experiment (of the order of minutes⁸ with the lower limit t_э≈10^-13s — the period of thermal vibrations of an atom); td t_д-durability (time to destruction); j_пл-deformation, increasing in the process of melting ice to its maximum. In (14) there is a deformation of the steady-state creep j_пл, varying from a certain minimum to a limit value at which complete destruction occurs (thawing of soil ice) - j_пл=j_пр= 0.083. In frozen soils of different composition, j_пр may be slightly more - 0.09... 0.14.⁸ The analysis showed good convergence of the results of calculations by the formula (14) with
actual data.^2-4 For example, Table 2 gives the relative strength of sandy loam P/Р_m at t=-10°C, with different durability (t, min), obtained with various types of tests experimentally,⁸ and calculated by the formula (14) at j_пл =0.11 and t_э=1min.

We can note that pressure; temperature, volumetric deformation and time enter into equation (14) equally, which implies their equivalence and interchangeability. Each of them can serve as a function and the rest act as arguments. It was shown above that any temperature of supercooling of soil moisture corresponds to the temperature of its future crystallization. I.e. the strength and deformation properties of the frozen soil can be approximately determined even when it is in the thawed state, substituting t_ф≈t_пер into (14).⁹

Formula (14) is a complete description of the process of deformation and destruction of plastic frozen soil. It differs from the well-known, firstly, by compliance with the kinetic concept of solid strength, naturally arising from the classical molecular kinetic theory, and secondly, by linking strength with phase equilibrium and deformation.

The authors declare that there is no conflict of interest.

1. Regel VR, Slutsker AI, Tomashevsky EE. The kinetic nature of the strength of solids. M: Nauka. 1974;15(1):560.
2. Konovalov AA. On the phase equilibrium and strength of frozen soils (single model). North Carolina, USA: Lulu Press, inc. 2016;151.
3. Konovalov AA, Roman LT. Features of the design of foundations in the oilfield regions of Western Siberia. L: Stroyizdat. 1981;167.
4. Roman LT. Frozen peat soils as engineering foundation constructions. Novosibirsk: Science. 1987;193.
5. Ershov ED. Laboratory methods for studying frozen soils. Moscow State University. 1985;351.
6. Grechishchev SE, Pavlov Ark V, Grechischeva OV. Regularities in the formation of supercooling of pore moisture during volumetric freezing of dispersed soils. Mat The third conference of geocryologists of Russia. M: MGU. 2005:38‒45.
7. Saveliev BA. Glaciology. M: MSU. 1991;288.
8. Vyalov SS. Rheological basis of soil mechanics. M: Higher School. 1978;448.
9. Konovalov AA. To the generalization of the parameters of cryogenic systems. Geoecology. 2017;2:89‒92.