Study region: It refers to the time series analysis of streamflow patterns in the six principal rivers of the Canal of Panama.

Study focus: Using recent time series modeling techniques in fractional or I(d) frameworks, it offer an insight into the hydrology of the Panama Canal watershed.

Objectives: The main objective is to determine if the river flows at the Canal of Panama watershed display long memory, and based on that, investigate if significant trends are present across time.

Novelty: The use of updated time series techniques in the analysis of long memory and time trends in river flow data.

New hydrological insights for the region: The results first indicate that long memory is present in all cases, with no significant trends whatsoever. While some series display evidence of seasonality, they are all mean-reverting. The implication of the results obtained is that climatological or hydrological shocks affecting these river streamflows may take a longer time to disappear.

Keywords: canal of Panama, river streams, long memory, persistence

JEL Classification: C22; C55; Y90.

MB, Mitochondrial diseases; mtDNA, mitochondrial DNA; MRI, magnetic resonance imaging; GTCS, generalized tonic-clonic seizure; HSV, herpes simplex virus; ENMG, electroneuromyography

In this article we investigate the long range dependence property in six river streams of the Canal of Panama watershed. This property, that produces high levels of dependence across data which are far away in time, has been proven to be present in many hydrological data since the seminal work by the famous hydrologist Harold E. Hurst. Hurst¹ examined the Nile river flows for the time period 641–1946, and noticed that long periods of dryness were followed by long periods of yearly returning floods, supporting this long term persistence effect. He then examined 600 time series that covered 75 different geophysical phenomena such as rainfall, atmospheric pressure, temperature etc., observing a similar pattern in all them. Since then, the stochastic modelling of river flows has produced numerous methods to explore the long memory or long range dependence property of the data. This long memory property is important because ignoring it may produce incorrect estimates in the remaining parameters of the model and thus erroneous conclusions about its behaviour. In this article, we focus on the rivers around the Canal of Panama watershed to examine the existence of time trends in the context of strong dependence models.

The Panama Canal is a man-made construction that connects the Atlantic and Pacific oceans, being one of the two most important strategic artificial waterways in the world. The Panama Canal watershed is the most important area of the country for Panama given the multiple uses it provides such as the continuous inter-oceanic navigation and generation of electric energy. The Canal watershed's main sub-basins include the Gatun reservoir and the Alajuela reservoir into which six principal rivers flow. The reservoirs are mainly used to store water needed for consumption by the population and the operation of the Canal. Making them one of the primary sources of water for the country.

There are many research projects which have studied the watershed, mostly with regard to contamination, dynamics of precipitation, physical controls, water management, and many more have focused in the sector of hydrology. Some of these issues are included in the Quadrennial report on regional progress and challenges in relation to the 2030 Agenda for Sustainable Development in Latin America and the Caribbean.² Some papers that study streamflows inside the Canal watershed utilize a time series method focused on deseasonalized anomalies and they use basic spectral techniques to study their relationship with El-Niño-Southern Oscillation (ENSO) and climate change in the region.³ On the other hand, the Canal of Panama Authority conducted a research based on sequential analysis technique (CUSUM), in which they analyzed the degree of deviation concerning the average of the streamflow series, observing positive tendencies, negative and stable periods from data taken inside the years 1934-2009, concluding no general tendency for the increase or decrease of the streamflows. Other studies reporting issues with respect to the Panama watershed include Harmon et al.,^4–8 etc. Nevertheless, none of these studies takes into account the potential long memory feature of the river flows at the Canal, which may produce biased results in terms of these trends.

Focusing on this perspective, we find only scarce literature based on streamflow time series for the case of the Canal Watershed. There are various studies that investigate long-memory streamflow properties for the Taiţa River (Rumania), the River Nile (Africa), and most of Canada’s major hydrologic regions.^9–11 Since streamflow is a water volume and velocity variable, there are various methods that deal with the variability of streamflow series exhibiting long-memory,^12,11 clearly based on the early works of Hurst¹ where many time series data in diverse fields of application, including hydrology, exhibited the property of long memory or long range dependence.

In this research work, we investigate the persistence or long memory feature within monthly streamflows from the six principal rivers of the Canal Watershed, by using fractional integration methods which address the degree of dependence in the data.¹³ This approach (fractional integration) is only one of the many models that satisfy the long memory feature but is very appropriate since throughout a single parameter (the differencing parameter, d) we can verify if the series of interest display such a property. The study utilizes monthly data provided by the Panama Canal Authority (ACP), between the periods of 1960 and 2020 to investigate the recent long memory dynamics and time trends present in the six main rivers of the Canal Watershed. The long-memory feature refers to a not negligible dependence between distant observations in time¹² and is a feature that is present in most of the climatological and geophysical time series.^14–17 Furthermore, the purpose of the paper is also to examine if time trends are present in the data using updated methods as proposed in Gil-Alana et al.¹⁸ and Awe and Gil-Alana¹⁹ among many others. Note that ignoring this long memory property can produce erroneous conclusions about the existence of time trends in the data.

The objectives of the paper are thus first to examine if long memory is present in the data, and based on this, investigate if the data display significant positive or negative trends across time. Our main results can be summarized as follows: evidence of long memory is found in the six rivers examined, however significant time trends were not found in any single case; high levels of strong dependence were found in the cases of Trinidad and Ciri Grande rivers while the lowest correspond to Boqueron and Pequeni. The rest of the paper is structured as follows: In Section 2, we present the materials and methods, including the area of study, the data and the methodology used in the paper. Section 3 displays the main results and the empirical analysis, while Section 4 renders the concluding remarks.

Study area

The Panama Canal Watershed has a surface of 3338 km² (Figure 1), which encompasses the two major sub-basins mentioned earlier, the Chagres, Pequeni, Boqueron, and Indio Este (not included in the study) rivers flow into the Alajuela reservoir with an area of 1026 km², while the rivers Trinidad, Gatun, and Ciri Grande makes their course for the Gatun lake compromising an area of 2312 km². Rio Chagres, Rio Pequeni, Rio Boqueron, Rio Gatun, and Rio Indio Este possess largely forested, steeply-sloping sub-watersheds on the north side of the Canal, while Rio Trinidad and Rio Ciri Grande are located at the south-west side of the watershed with mostly deforested areas.⁷ These river flows are affected especially by precipitation increases, the rainy season of Panama has a long duration, from May to November^20,21 and the dry season typically occurs from December to April,^22,23 precipitation is twice as high on the Atlantic coast side (Bahia de Panama) as on the Pacific coast (Mar Caribe) side with a difference of 4,000mm/year compared to 1,800mm/year.⁷

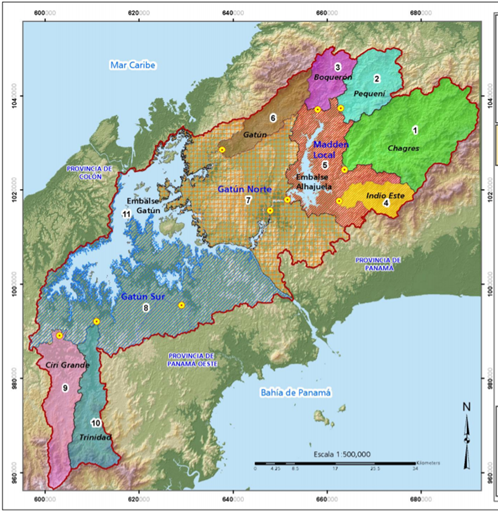
Figure 1 Canal of Panama Watershed area highlighted with a red line. While each river basin is highlighted with a specific color seen above. (Source: Hydrological Report, ACP, 2019)

Data

The data employed in this work were provided by the Panama Canal Authority through the department of Hydric Resources, which include monthly streamflows from six hydrometric stations located on the watershed principal rivers Rio Chagres, Pequeni, Boqueron, Gatun, Trinidad, and the Rio Ciri Grande. The data from January 1960 and onwards from the streams is measured in cubic meters per second (m³/s), which is acceptable for most practical purposes when calculating water flow. As the data are raw, there is a possible appearance of a trend and seasonal effect, which can be explained because the rivers volumetric flow rate is affected by several regional hydrological cycles that are determined by the climate conditions, such as water supply (precipitation) and energy availability (potential evapotranspiration), and regulated by corresponding underlying characterizations, such as vegetation, soil and geography.²⁴ Figure 2 displays plots of the six time series in which we can observe a clear seasonal pattern, while we can also observe a stationary pattern for most of the streamflow series.

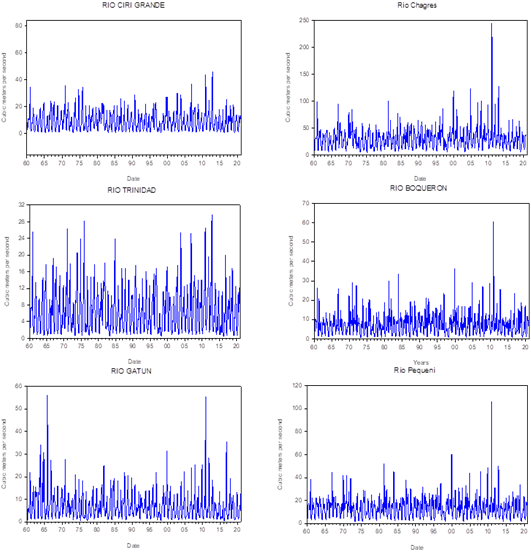
Figure 2 Time series plots for the streamflow data (m³/s). Vertical axis of the plat is the amount of water in cubic meters per second, while horizontal axis is the years in monthly time frequency. The horizontal axe refers to the years, while the vertical axe refers to cubic meters per second.

Methodology

Long memory is defined in the time domain in terms of decay rates of long-lag autocorrelations; in other words, it is a feature that indicates a high level of dependence between observations that are far apart in time. As mentioned before, we will use a long range dependence approach that is based on integrational processes or I(d) models, which have been widely used in the analysis of hydrological and climatological data.^{25–27,18,19} Long memory structure in a covariance stationary process may be characterized via an autocovariance sequence, or by its spectral density function. More in detail, we say that Y_t is a stationary long memory process if there exists a real number -1 < β < 0 and a constant C_s > 0 such that

$\underset{T\to \infty }{\lim }{S}_{\Upsilon ,\tau }\frac{S_{\Upsilon ,\tau }}{C_s{\tau }^{\beta }}=1$   (1)

being $S_{\Upsilon ,\tau }$  the autocovariance sequence and $\tau$  the differences in time.²⁸¹ Various methods are available to detect the existence of long-memory. Some of them are parametric, while others are semiparametric or even non-parametric. In this work we use a parametric approach based on fractional integration, estimating the fractional differencing parameter d, an approach widely used when modeling persistence in hydrological time series.

An I(0) process u_t, t = 0, ± 1, … , is defined as a covariance stationary process with spectral density that is finite and positive at the zero frequency. Then a process, {x_t , t = 0, ±1, … , } which is integrated of order d, and expressed as I(d) is described by the following equation:

${(1-B)}^d{x}_t=u_t,t=1,2,\mathrm{...},$   (2)

where $u_t$  is an I(0) process;  is the backshift- (or lag-) operator, $B{x}_t=x_{t-1},$  while d is any real number playing a very important role in determining the level of association between $x_t$  and its lagged values. By allowing d to be any real value, it can also be fractional and cover the standard cases of nonstationarity unit roots I(1) and stationarity I(0) if the differencing parameters are equal to 1 and 0 respectively. The polynomial ${\left(1-B\right)}^d$  in Eq. (2) can be expanded in terms of a binomial representation, such that

${(1-B)}^d={\displaystyle \sum _{j=1}^{\infty }\left(\begin{array}{l}d\\ j\end{array}\right){(-1)}^j{B}^j}=1-dB+\frac{d(d-1)}{2}{B}^2-\frac{d(d-1)(d-2)}{6}{B}^3+\mathrm{....}$   (3)

and thus

${(1-B)}^d{x}_t=x_t-d{x}_{t-1}+\frac{d(d-1)}{2}{x}_{t-2}-\frac{d(d-1)(d-2)}{6}{x}_{t-3}+\mathrm{....}$   (4)

implying that Eq. (1) can be represented as

$x_t=d{x}_{t-1}-\frac{d(d-1)}{2}{x}_{t-2}+\frac{d(d-1)(d-2)}{6}{x}_{t-3}-\mathrm{....}+u_t$ .  (5)

Remembering that d is an indicator of the level of dependence of the data, in the sense that the higher the value of d is, the higher the degree of the association will be between the observations. When 0 < d < 0.5, the spectral density function has a singularity at 0, displaying the property of “long memory”, because the process exhibits slowly decaying autocovariance as originally introduced by Granger and Joyeux.²⁹ These processes have been widely employed in recent years in the analysis of hydrological data.^30–33,12

We estimate the differencing parameter d in equation (2) using the Whittle function, which is basically an approximation to the likelihood function and use a frequency domain version of it as in Dahlhaus³⁴ alongside a testing procedure developed by Robinson³⁵ which is based on the Lagrange Multiplier (LM) principle. This method tests the null hypothesis,

$H_o:d=d_o,$  . (6)

for any real value do, in the following set-up:

$y_t=\beta \text{'}{Z}_t+x_t,{\left(1-B\right)}^d{x}_t=u_t,$   (7)

where z_t is a set of non-stochastic terms and x_t are the errors in the regression model which are supposed to be I(d). Robinson³⁵ showed that the test statistic follows asymptotically a N(0,1) distribution, independently of the value of d_o and the choice of the deterministic terms. The specific functional form of this method can be found in Gil-Alana and Robinson.³⁶

¹Alternatively, long memory is defined in the frequency domain if its spectral density function goes to infinity at some frequencies in the interval [0, π).

We consider the model described by equation (7) with z_t = (1, t)^T to allow for a constant and a linear time trend, so the estimated model is the following one:

$y_t={\beta }_0+{\beta }_{1}t+x_t,{\left(1-B\right)}^d{x}_t=u_t,u_t=\varphi u_{t-12}+{\epsilon }_t,$   (8)

where $y_t$  refers to each time series we observe, β₀ and β₁ refer respectively to the constant and a linear time trend, and the regression errors,$x_t$ are integrated of order d or I(d) such that the short memory errors $u_t$  follow a seasonal (monthly) AR(1) model, with ${\epsilon }_t$  as a white noise process. Anticipating the results, the time trend is not required in any single case, the intercept being sufficient to describe the non-stochastic part. The estimates of d are all in the (0,1) interval, implying long range dependence (d > 0) and fractional integration with a mean reverting pattern.

Table 1 reports the estimated values of d in three scenarios: with no regressors, with an intercept, and with an intercept and a linear time trend. Bold numbers in the table indicate the most significant model according to these non-stochastic terms. It is observed that evidence of stationarity (d < 0.5) is found in the cases of the Boqueron, Pequeni, Chagres and Gatun rivers, while for the Ciri grande and Trinidad, the confidence bands include both stationary and nonstationary values. While the time trend is found to be statistically insignificantly different from zero in all cases, we can see that in all cases that there is evidence of mean reversion (d < 1). We observe similar patterns in all cases for the six principal rivers, where long memory is present, given that the estimated value of d is significantly positive, rejecting the I(0) null hypothesis of short memory (d = 0). Table 2 displays the coefficients for the selected estimated model in each river streamflow, showing that the seasonal component is higher for the cases of the Trinidad and Gatun, followed by the Ciri Grande. Nevertheless, the coefficients and test statistics within the Chagres river should be taken with caution given that the river streamflows are affected by the Gatun Dam, which can alter the low flow regime and reduce peak flows.³⁷

As mentioned before, streamflow is mainly affected by precipitation and evapotranspiration, creating an extensive effect on water flows of these rivers. The department of Hydric Resources and Water Quality division is responsible of monitoring and controlling the water flows in these regions. Furthermore, The ACP research on the study behavior of these streamflows in 2009 composed data from our six stations that included years from 1934-2009. Identifying certain tendencies in the stations, separating them between different periods in time (e.g., 1934-1956; 1957-1965) concluding that conducting a study between certain periods in time will lead to a positive, negative, and neutral tendencies inside those estimated periods. They applied statistical differences with the following simple formula:   

$X_t=\frac{S_t-A_{t-1}}{A_{t-1}},$   (9)

being $S_t$  the average annual streamflow with respect to year t, representing the annual streamflow historic average, while $X_t$  refers to the difference in streamflow contribution in contrast to the annual streamflow historic average.

Table 3 is a descriptive table (taken and updated from ACP Water and Jungle report, pg.12, 2009), in which we can see an updated summary from tendencies and differences in annual streamflow contributions from the six river flow stations.

From Table 3 we observe strong patterns inside certain specific periods, for Rio Ciri Grande and Trinidad we have an increasing, decreasing, increasing, and a neutral tendency for specified periods in time, which can be explained due to seasonality as the previous statistic model suggested. As long memory is present in all six river stations, there is strong persistence (long memory) that can affect the categorized tendencies. This is very important because the discharge of these rivers affects the water levels of the Gatun and Alajuela lakes, whose main use is for the transit of commercial ships (Gatun) and provision of drinking water for 55% of the population in Panama (Alajuela) (IDB, 2020). Gatun Lake receives its water from precipitation and streamflows of the Trinidad, Gatun, and Ciri Grande rivers, which suffer from the highest seasonal components and long memory, meaning that shocks in these three river flows may take a longer time to disappear even though their streamflows are mean-reverting. On the other hand, streamflows of the Chagres, Pequeni, and Boqueron rivers end up in the Alajuela lake, whose annual water contributions are lower than Gatun lake, which is explained logically because of their huge difference in surface area and the Madden Dam that impounds the Chagres river. Although the rivers on this side of the watershed tend to have lower water contributions, seasonality and long memory also affect them, with strong implications especially for the Chagres river which is dammed twice, resulting in the reservoir to Gatun Lake and Alajuela, forming one of the principal sources of regulation for navigation runoff for the operation of the Panama Canal.

Therefore, if a climatological shock like the phenomenon of El Niño-Southern Oscillation (ENSO)² is present, it can have a major effect on the streamflow of the rivers with a higher degree of persistency, and a lower effect for those which possess short memory (d = 0). Even though all our river flows are mean-reverting (d < 1), the annual average streamflows with respect to the historic average annual streamflow from 2015 has been negative for most of these rivers (Appendix), which is no surprise as long memory is present (d > 0) in all of our studied rivers implying that shocks caused by climatological and hydrological factors may take longer to disappear completely.^38–44

²The ENSO is a warming of the ocean surface, or above-average sea surface temperatures in the central and eastern Tropical Pacific Ocean. This affects global climate and can lead to intense storms in some places and droughts in others. Source: https://www.weather.gov/mhx/ensowhat

The fractional integrated techniques introduced here provide a method to detect the presence of long memory in time series. The model allows for both long-memory and short-memory non-seasonal and seasonal components such as persistence, time trends, and seasonality. In this article, the long-memory properties in streamflows at the Canal Watershed have been investigated in six river stations, providing streamflow data from the Chagres, Pequeni, Boqueron, Ciri Grande, Trinidad, and Gatun rivers. We observe that the distribution of streamflows for Trinidad, Gatun, and Ciri Grande offers the highest seasonality, nevertheless, there is no time trend found in any of the series. Dealing with the order of integration of the series, the results indicate that long memory or high persistence is found in all cases, with Gatun, Chagres, Trinidad, and Ciri Grande being the highest while short memory or I(0) cannot be found in any case, all series displaying mean-reverting patterns. Although no time trends were found in our study, there exist certain tendencies for specific periods in time. Thus, for example,

1. Seasonality is important for Trinidad, Gatun, and Ciri Grande and their patterns can affect streamflow for prolonged periods, water contributions to their respective reservoir. 
2. All cases suffer from long memory, and complementary attention should be given to the Chagres River that along with Trinidad display the highest degrees of integration, as it is in fact one of the largest rivers and it provides sources of water for both the Alajuela and Gatun lakes.
3. It should also be noted that Trinidad and Ciri Grande are the river areas that suffer the most from deforestation.
4. Complementary work should be conducted on the long memory persistence properties by suing alternative methods in these and in other time series data dealing with rainfall and temperatures inside these specified river areas.

The instruments utilized in this study can provide explicit information to policymakers regarding changes in future hydrological patterns in these regions. Finally, other lines of research still based on long memory processes can be implemented in these series. Thus, for example, the possibility of non-linear structures or structural breaks are relevant issues that may be worthy of our attention since several authors have argued that fractional integration may be an artificial artifact generated by the presence of breaks which have not been taken into account. Non-linear deterministic structures like those based on Chebyshev’s polynomials in time proposed by Cuestas and Gil-Alana (2016) or Fourier transforms (Gil-Alana and Yaya, 2020) or even neural networks as in Yaya et al. (2021) can be implemented in these and other data.

The authors gratefully acknowledge the provision and support of data by the Panama Canal Administration.

The author declares there is no conflict of interest.

1. Hurst HE. Long-term storage capacity of reservoirs. Trannsactions of the American Society Civil Engineers. 1951;116(1):770–779.
2. UNSDG (United Nation Sustainable Developing Group). Quadrennial report on regional progress and challenges in relation to the 2030 Agenda for Sustainable Development in Latin America and the Caribbean. Forum of the Countries in Latin America and the Caribbean on the Sustainable Development, Santiago de Chile. 2019.
3. Amador JA, Olmedo BA. Temperatura, Precipitación y Caudal en Panama. Parte ll: ENOS y Cambio climático. Tópicos Meteorologicos y Oceanograficos. 1998;5(2):136–148.
4. Harmon RS. An Introduction to the Panama Canal Watershed. In: Harmon RS. Editor. The Río Chagres, Panama. Water Science and Technology Library, vol 52. Springer, Dordrecht. 2005.
5. Carse A. Nature as infrastructure: Making and managing the Panama Canal watershed. Social Studies Science. 2012;42(2):539–563.
6. Simonit S, Perrings C. Bundling ecosystem services in the Panama Canal watershed. PNAS. 2013;110(23):9326–9331.
7. Smith DF, Goldsmith ST, Harmon BA, et al. Physical controls and ENSO event influence on weathering in the Panama Canal Watershed. Scientific Reports. 2020;10:10861.
8. Valdelamar-Villegas J, Gomez H, de la Rosa JD, et al. Multi-elemental composition and toxicity of bottom sediments from Panama Canal watershed. Ocean and Coastal Management. 2021;204(15):105459.
9. Montanari A, Rosso R, Taqqu MS. A seasonal fractional ARIMA model applied to the Nile River monthly flows at Aswan, Water Resources Research. 2000;36(5):1249–1259.
10. Ehsanzadeh E, Adamowski K. Trends in timing of low stream flows in Canada: impact of autocorrelation and long-term persistence, Hydrological Processes. 2010;24(8):970–980.
11. Maftei C, Barbulescu A, Carsteanu AA. Long-range dependence in time series of Taita River discharges, Hydrological Sciences Journal. 2016;61(9):1740–1747.
12. Hadizadeh R, Eslamian S, Chinipardaz R. Investigation of long-memory properties in streamflow time series in Gamasiab River, Iran. International Journal of Hydrology Science and Technology. 2013;3(4):319–350.
13. Box-Steffensmeier JM, Tomlinson AR. Fractional integration methods in political science. Electoral studies. 2000;19(1):63–76.
14. Percival DB, Overland JE, Mofjeld HO. Interpretation of North Pacific variability as a short- and long-memory process. Journal of Climate. 2001;14:4545–4559.
15. Gil-Alana LA. Statistical model for the temperatures in the Northern hemisphere using fractional integration techniques. Journal of Climate. 2005;18:5357–5369.
16. Gil-Alana LA. Time trend estimation with breaks in temperature time series. Climate Change. 2008;89:325–337.
17. Gil-Alana LA. Alternative modelling approaches for the ENSO time series. Persistence and seasonality. International Journal of Climatology. 2017;37:2354–2363.
18. Gil-Alana LA, Monge M, Romero F. Sea Surface temperaturas. Seasonal persistence and trends, Journal of Oceanic and Atmospheric Technology. 2019;36(12):2257–2266.
19. Awe OO, Gil-Alana LA. Fractional integration analysis of precipitation dynamics: empirical insights form Nigeria. Tellus A: Dynamic Meteorology and Oceanography. 2021;73(1):1–9.
20. Enfield DB, Alfaro EJ. The dependence of Caribbean rainfall on the interaction of the tropical Atlantic and Pacific Oceans. Journal of Climate. 1999;12:2093–2103.
21. Kusunoki S, Nakaegawa T, Pinzon R, et al. Future precipitation changes over Panama projected with the atmospheric global model MRI-AGCM3.3. Climate Dynamics. 2019;53:5019–5034.
22. Mitchell TP, Wallace JM. The Annual Cycle in Equatorial Convection and Sea Surface Temperature. Journal of Climate. 1992;5(10):1140–1156.
23. Nakaegawa T, Arakawa O, Kamiguchi K. Investigation of climatological onset and withdrawal of the rainy season in Panama Based on a daily gridded precipitation dataset with a high horizontal resolution. Journal of Climate. 2015;28:2745–2763.
24. Zhang D, Madsen H, Ridler ME, et al. Multivariate hydrological data assimilation of soil moisture and groundwater head. Hydroogy Earth System Sciences. 2016;20:4341–4357.
25. Corduas M, Piccolo D. Short and long memory unobserved components in hydrological time series, Physics and Chesmitry of the Earth. 2006;31(18):1099–1106.
26. Rea W, Reale M, Brown J. Long memory in temperature reconstructions. Climatic Change. 2011;107:247–265.
27. Rypdal K. Attribution in the presence of a long memory climate response, Earth System Dynamics. 2015;6:719–730.
28. Beran J. Statistics for Long-Memory process, vol. 61, Monographs on Statistics and Applied Probability, Chapman and Hall, New York, 1994. p. 315.
29. Granger CWJ, Joyeux R. An introduction to long memory time series and fractional differencing. Journal of Time Series Analysis. 1980;1:15–29.
30. Montanari A, Rosso R, Taqqu MS. Fractionally differenced ARIMA models applied to hydrologic time series: Identification, estimation, and simulation, Water Resources Research. 1997;33(5):1035–1044.
31. Witcher B, Byers D, Guttorp P, et al. Testing for homogeneity of variance in time series: Long memory, wavelets, and the Nile River. Water Resources Research. 2002;38(5):1054.
32. Chen C, Tian Y, Zhang YK He. Effects of agricultural activities on the temporal variations of streamflow: trends and long memory. Stochastic Environmental Research and Risk Assessment. 2019;33:1553–1564.
33. Ledvinka O, Recknagel T. Long-term persistence in discharge time series of mountainous catchments in the Elbe River basin. Proceedings of the International Association of Hydrological Sciences. 2020;383:135–140.
34. Dahlhaus R. Efficient parameter estimation for self similar process. Annals of Statistics. 1989;17:1749–1766.
35. Robinson PM. Efficient Tests of Nonstationary Hypotheses. Journal of the American Statistical Association. 1994;89(428):1420–1437.
36. Gil-Alana LA, Robinson PM. Testing of unit root and other nonstationary hypotheses in macroeconomic time series. Journal of Econometrics. 1997;80:241–268.
37. Mailhot A, Talbot G, Ricard S, et al. Assessing the potential impacts of dam operation on daily flow at ungauged river reaches, Journal of Hydrology: Regional Studies. 2018;18:156–167.
38. ACP-EU Natural Disaster Risk Reduction Program 2020-2021. Activity Report ACP-EU Natural Disaster Risk Reduction Program 2020-2021 Activity Report2 3. 2021.
39. Cuestas JC, Gil-Alana LA. Testing for long memory in the presence of non-linear determinisctic trends with Chebyshev polynomials. Studies in Nonlinear Dynamics and Econometrics. 2016;20(1):57–74.
40. Espinosa D. Aguas y bosques en la cuenca del canal: tendencias de largo plazo. 2009. p. 18–49.
41. Garcimartin C, Astudillo J, Garzonio O. El agua en la economia de Panama. Inter-American Development Bank. 2020.
42. Gi-Alana LA, L Sauci. US temperatures. Time trends and persistence. International Journal of Climatology. 2019;39(13):5091–5103.
43. Gil-Alana LA, Yaya O. Testing fractional unit roots with non-linear smooth break approximations using Fourier functions. Journal of Applied Statistics. 2020;48(13–15):2542–2559.
44. Yaya O, Ogbonna AE, Gil-Alana LA, et al. A new unit root analysis for testing hysteresis in unemployment. MPRA Paper, 96621, University Library of Munich, Germany. 2021.