This study involves the application of ratio method of hydrological data transposition for flood and rainfall frequency analysis for ungauged catchments. For the flood transposition, a gauging station, River Niger at Onitsha about 166.9km to an ungauged station, Taylor creek, both in Niger Delta were selected. Onitsha station has been established since 1914 with historic discharge records. For the Taylor creek there was evidence of bank erosion that prompted the early study on bank protection design options, either revetment or vertical face retaining wall. The Design element would require flood frequency analysis for determination of flood events such as 10, 50 and 100 year flood flows. Through bathymetric survey and velocity measurements rating curves were established for Taylor creek; at various depths discharges for Taylor creek and River Niger at Onitsha were computed with corresponding ratios. The overall average ratio is 9:100, that is, 9 percent of River Niger is equivalent to flow in Taylor creek. This ratio permitted 30years of records at Onitsha station to be transposed to Taylor creek. Analogous to ratio approach on stream flows, rainfall intensity duration frequency (IDF) models in Port Harcourt were transposed to Peremabiri by ratio 1:1.2. Both rainfall stations are in Niger Delta, Nigeria.

Keywords: hydrological data transposition, flood, rainfall IDF models, river Niger, Taylor creek

Transposition is a technique for relocating or transferring isohyetal pattern of storm precipitation within a region that is similar relative to terrain or environmental and meteorological (or climatological) features principal to the particular storm rainfall concerned. A review of pertinent literature shows that transposition has greatly increases the availability of data for evaluating rainfall potential for drainage. The factor which control limits to storm transposition are topography, storm isohyetal charts, weather maps, storm tracks and rainfalls of record for the type of storm under consideration and topographic charts.¹ There are basically three steps in transposition; meteorological analysis, the determination of the transposition limits and the application of the appropriate adjustments for the change in storm location. The concept of storm transpostion has been applied in various hydrological studies. Foufoula-Georgious² developed a probability storm transposition method which systematically uses storm and basin data to estimate extreme precipitation frequencies. The author viewed this as the first step in evaluating the extreme flood probabilities required to apply many risk-analysis methodologies. The method was applied to two hypothetical catchments in Iowa.

The resultant depth-exceedance probability curve was smooth, suggesting that extrapolating the curve to very rare events may be promising. Portela³ proposed the application of storm transposition to tackle the limitation of sufficient storm data for the development of a small hydropower sheme by getting hydrologic data from a gauge station with same meteorological characterisitc in Ireland. Also, in November 2004, the Alberta Transportation⁴ applied storm transposition concept in developing guidelines for extreme flood analysis which would solve the problem of apparent inconsistencies in estimates of Probable Maximum Flood and probability-base extreme floods employed in the design and evaluation of major hydraulic structure. England et al.⁵ worked on an integrated data-modeling of hydrologic hazard framework for physiclly-based extreme flood hazard estimation applying transposition technique. The study area for this work was the 12,000km² Arkansas River watershed in Colorado. The study demonstrated that the size and location of extreme storms are critical factors in the analysis of basin-average rainfall frequency and flood peak distributions. The resultant runoff model was substantially improved by the availability and use of paleoflood nonexceedance data spanning the past 1000 years at critical watershed locations. Gan et al.⁶ investigated different forms of the regressional relationship between the concurrent monthly discharges of neigbouring catchments with the view to generalising th relationship for a region. This enables monthly streamflow data to be transposed from a gauged catchment to an ungauged catchment, provided the certain transfer coefficient can be estimated from the physical catchment and rainfall characteristics. This may be estimated in a number of ways for a pair of gauged – ungauged. However, errors in the individual transferred flows are high. The aim of this study is to apply a simple hydrological data transposition appraoch, a ratio method of finding the average ratios of peak flows between gauged and unguaged stations. For the unguage station, it is a matter of field measurements carried out at a period coincident with those of the gauged station. Both the guaged and ungauged stations are in the Niger Delta having similar terrain and meteological featurs. Apart from stream flows, is that of rainfall data for a gauged station which facilitated the development of rainfall-intensity-duration-frequency (IDF) models and a nearby gauging station having monthly rainfall totals and no durations recorded. This is the case of Port Harcourt and Peremabiri cities in Niger –Delta. In this case, rainfall IDF model transposition is possible by ratio method.

Study area

The study area is within Niger Delta in Southern Nigeria bordering with Atlantic Ocean and it covers the River Niger gauging station at Onitsha, Taylor Creek at Koroama and Peremabiri town (Figure 1). Taylor Creek is a tributary of Nun River, also, a tributary of River Niger. The Onisha gauging station is located upstream of the highway bridge at Latitude 06º 10´ and Longitude 06º 45´ and on the left bank of the River Niger. The gauging station was established in 1914 and being operated by the Nigerian Inland Waterway Authority (NIWA). The highest of the gauging station is 25.41m above mean sea level. Taylor creek station is 166.9km from the Onitsha gauging station. The site lies between Longitude 06º 17´to 06º 21´E and Latitude 05º 01´ to 05º 15´N. The elevation is 8m above mean sea level (MSL).

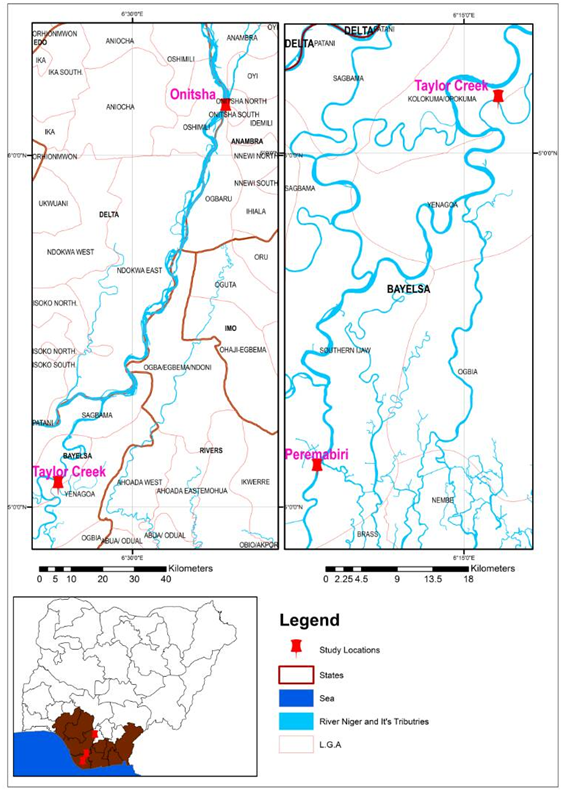
Figure 1 Map showing the study area, locations of Onitsha gauging station, peremabiri and Taylor creek basin.

Data collection

Data collection consists of two aspects:

1. Collection of hydrological data from hydrological year-books compiled by NIWA, lokoja Nigeria, for flood frequency analyses and development of rating curves,⁷
2. Hydrographic and bathymetric surveys were also conducted in compliance with BS3680-3B:1997. Once a current meter has been selected and a cross-section for discharge measurement established, the cross-section was divided into vertical sections.

In general, no one vertical section included more than 10 percent of the total flow, thus, a minimum of ten verticals per cross-section were employed for mean discharge estimation. Velocity measurements were carried out using current meter located at 0.2, 0.6 and 0.8m depths below the water surface.

Data analyses

Cross-sectional velocity &discharge computations

The mean velocities in each vertical segment were calculated according to the formula:

$\underset{}{\overset{\_\_}{V}}=\frac{1}{3}\left(V_{0.2}+V_{0.6}+V_{0.}{}_8\right)$ (1)

Where: V_0.2, V_0.6 and V_0.8 are point velocities calculated at 20%, 60% and 80% of the depth.

Data transposition for discharge or rainfall gauged to ungauged stations was facilitated by use of discharge or rainfall ratios between both stations. Temporary discharge or rainfall measurements are necessary for the ungauged stations to match the same period of time (rainfall period) for the gauged station in other to validate the computation of rainfall or discharge ratio. Two methods were adopted for discharge computation namely the mean section method and the mid-section method according to Equations 2 & 3, respectively.

$Q={\displaystyle \sum q_i={\displaystyle \sum \stackrel{\_\_}{V}}}A={\displaystyle \sum _{i=1}^m\left(\frac{{\overline{v}}_{i-1}+\stackrel{\_\_}{V}{}_i}{2}\right)}*\left(\frac{d_{i-1}+d_i}{2}\right)\left(b_i-b_{i\text{}-1}\right)$ (2)

and

$Q={\displaystyle \sum q_i={\displaystyle \sum \stackrel{\_\_}{V}}}A={\displaystyle \sum _{i=1}^m{\stackrel{\_\_}{V}}_{idi}}\left(\frac{b_i-b_{i\text{}-1}}{2}\right)$ (3)

where:    Q is the calculated total discharge; b_i is the width of the i^th Section; d_i is the depth of the i^th Section$\stackrel{\_\_}{V}$ ; is the mean velocity in the i^th vertical; m is the total number of sections; q_i is the calculated segment discharge; and b_i–1, v_i–1, d_i–1 refers to the previous section. Although, both methods were employed in discharge computations for comparison purposes. The Q values obtained using the mid-section was used for flood frequency analysis. The mid-section values were generally higher.

Stage-discharge equation

The rating curves were developed according to BS 3680:3c⁸ & BS ISO⁹. The stage-discharge relation was expressed by an Equation of the form:

$Q=C{h}^{\beta }$ (4)

Where: Q is the discharge, h is the gauge height and C and β are coefficients, over the whole range of discharges.

If the zero of the gauge does not coincide with zero discharge, as the case of Taylor Creek, a correction factor, “a” must be applied to h, as depicted in Equation (5).

For the determination of factor, “a” three values of discharge Q₁, Q₂ and Q₃ are selected in geometric progression. i.e.

$Q_2^2=Q_1{Q}_3$ (6)

If the corresponding values of the gauge or depth readings from the curve are h₁, h₂ and h₃, it is possible to verify that:

$\text{a}=\frac{{{\displaystyle h}}_2^2-h_1{h}_3}{h_1+h_3^{}-2h_2}$ (7)

Flood frequency analysis

Log-Pearson Type III and Gumbel Extreme Value Type I were the basis of flood frequency analysis, to obtain the design flood for return period of 10, 50 and 100-yrs.¹⁰

Log-Person type III

For Log Pearson Type III parameter estimate, we have Equations (8 – 11):

$Mean=Log\overline{Q}=\frac{{\displaystyle \sum LogQ}}{n}$ (8)

Standard deviation, ${\sigma }_{LogQ}=\sqrt{\frac{{{\displaystyle \sum }}^{\text{}}{\left(LogQ-Log\overline{Q}\right)}^2}{n-1}}$ (9)

Skew Coefficient, $Gs=\frac{n{\displaystyle \sum {(LogQ-\stackrel{\_\_}{\log Q})}^3}}{(n-1)(n-2){({\sigma }_{LogQ})}^3}$ (10)

where: Q=value at any probability level is obtained as:

where K_T=coefficient for the Log-Pearson Type III; $\overline{Q}$ = Mean of Logs of annual floods;

${\sigma }_{LogQ}$ =standard deviation of Logs of annual floods; and G_s = coefficient of skewness of logs of annual floods.

Gumbel extreme value type I (EV1)

The probability density function of Gumbel extreme value type I distribution is given by

$f\left(x\right)=exp\left\{-\left(x-\alpha \right)/\beta -exp\left(-\left(x-\alpha \right)/\beta \right)\right\}/\beta$ (12)

The cumulative Density function

$F\left(x\right) exp\left\{-exp\left\{-\left(x-\propto \right)/\beta \right\}/\beta \right\}$ (13)

Velocity measurement & discharge computation

Cross-section number eleven (CS11) was used for the discharge computation and development of stage-discharge relation for Taylor creek. The velocities and depths for the cross-section are shown in Table 1. Equations (2) and (3) were applied to Table 1 for discharge computations. Tables 2, Table 3 show the calculation procedures and the discharge values obtained. Water depths above Low-Low Waters (LLWs) were varied at intervals of 0.5m, until the depth/discharge table was obtained (Table 4). Data in Table 4 were used to generate the Depth-discharge curves for Taylor Creek.

Development of depth-discharge relation

Given the discharge and stage (depth) values from a typical rating curve for Taylor creek, Equation (5) is calibrated for values of C and β. However, the constant “a” is evaluated via Equation (7). In other to estimate the value of “a” of Equation (7), we select from Table 3, h₁=6.94 m, h₂=8.94m and h₃=11.44m. Thus

The values of C and β in Equation (5), are obtained by linear regression modeling, after logarithmic linearization. Equations (14 & 15) are the resulting logarithmic normal equations,^11‒13 & shows in Table 5.

$\sum logQ=NlogC+\beta \sum \left(logh–a\right)$ (14)

$\sum logQlog\left(h-a\right)=\sum log\left(h-a\right)logC+\beta \sum {\left[log\left(h–a\right)\right]}^2$ (15)

Using Table 4, Equations (14) and (15) become:

$27.6865=LocC+9.01314\beta$ (16)

$24.9966=9.01314LogC+8.18505\beta$ (17)

Solving Equations (16) and (17) simultaneously gives:

                Log C = 2.126 or C = 133.66; and β = 0.70368.

 Thus,

$Q=133.66{\left(h–1.1\right)}^{0.70368}$ (18)

Discharge transposition for Taylor creek

Bank erosion for Taylor creek at Koroama was of concern that prompted a study on possible bank protection works (revetment or vertical face retaining wall). For instance, the revetment design elements would require flood frequency analysis for determination of flood events such as Q₁₀, Q₅₀ and Q₁₀₀. Given non-existent historic data on Taylor Creek, the need to transpose River Niger discharges with over 30 years of records was necessitated. Rating curves for both Taylor Creek and River Niger were plotted for sake of comparison and establishment of flow ratios or weighting (Figure 2). Taylor Creek discharges were obtained for 30 years by analyzing the mean ratio of its discharges with those of River Niger at corresponding depths (Table 6). On the average, 9% of River Niger discharge is equivalent to that of Taylor Creek. The flow transposition approach exemplified in this study is possible given that the gauged station (Onitsha) and ungauged station (Taylor Creek) are within Niger Delta, having similar meteorological features. The approach is simple as compared with methods proposed by Foufoula-Georgious,² Portela,³ & Gan et al.,⁵ It is also interesting to note that Foufoula-Georgious² proposed the probability storm transformation approach, While Gan et al.⁵ worked on regressional relationships for monthly streamflow data, for which high errors were observed.

Figure 2 Stage- discharge plots for Taylor creek and river Niger.

Log Pearson type III & gumbel extreme value type I flood frequency predictions

The Taylor Creek discharges taken as 9% of River Niger discharges for 30 years period are as presented in Table 7. Equations (8-10) are evaluated using Table 6 for Taylor Creek, as:

Standard deviation $s_{logQ}{}^{=}{\left[\frac{{\displaystyle \sum {(Log\text{Q}-\text{Q})}^2}}{n-1}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}={\left[\frac{0.34492}{29}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=0.11$

Skew coefficient $\left(G\right)=\frac{n{\displaystyle \sum {(Log\text{Q}-Log\text{Q})}^3}}{(n-1)(n-2)\text{}({\sigma }_{Log}){}^3}=\frac{30(-0.009156903)}{29x28x{(0.11)}^3}=-0.254$

Adopting Equation (11) for flood frequency modeling, we have skew coefficient (Gs) of -0.254, return periods (T) of 10, 50 & 100 years, the corresponding K_T values are for 10 year flood, K_T = 1.252; 50 year flood, K_T = 1.918 and 100 year flood; K_T = 2.141; Thus,

Thus,

Q₁₀=Antilog (3.2504155)=1971m³/sec

Q₅₀=3.156859+1.918 (0.11)=2332 m³/sec

Q₁₀₀=3.156859+2.141 (0.11)=2468.1m³/sec

Gumbel extreme value type 1 parameters and predictions

For the Extreme Value Type 1 distribution, the K_T values were obtained as follows:

$K_T=\frac{-\sqrt{6}}{\Pi }\left[0.5772+\ell n\left[\ell n\left(\frac{T}{T-1}\right)\right]\right]$ (19)

Where: K₁₀=1.305; K₅₀=2.608; and K₁₀₀=3.1445 and

$Q_T= \stackrel{\_\_}{{\displaystyle \text{Q}}}+K_{T}S$ (20)

where S=standard deviation, and S is calculated from data (Table 7), thus:

Q₁₀ =1478.3+1.305 (359.3)=1947.2

Q₅₀ =1478.31+2.608 (359.3)=2415.4

Q₁₀₀ =1478.31+3.1445 (359.3)=2608.1

Results comparison of Gumbel and log–Pearson III

% Difference at 10 and 100 years:

Errors between the two distributions are within 10% limit, thus they are both acceptable. However, we recommend the Log-Pearson III values for design purposes Table 8.

Developing IDF models by rainfall transposition

Rainfall Transposition between Peremabiri and Port Harcourt is possible (Figure 3). The rainfall Intensity-Duration-Frequency (IDF) models for Port Harcourt were transposed by multiplying with a conversion factor of 1.2 to obtain the equivalent for Peremabiri in Taylor Creek basin. The rainfall distribution of Port Harcourt and Peremabiri were assumed to be similar in this study by reason of nearness and both are in the Niger Delta with same meteorological conditions. The average of the ratios of annual rainfall amounts in Peremabiri and that of Port Harcourt yielded 1: 1.2. That is 1mm of rainfall in Port Harcourt as equivalent to 1.2mm in Peremabiri. In effect, rainfall models for Port Harcourt are multiplied by a factor of 1.2 to obtain that of Peremabiri (Table 9).

Figure 3 Plot of annual rainfall for peremabiri and Port Harcourt (1963 - 1981).

Based on this study the following conclusions can be drawn:

1. The hydrological data transposition between a gauged station at Onitsha and ungauged station at Taylor creek both in Niger Delta with similar meteorological conditions was possible using discharge ratio method. The use of rating curves for both gauged and ungauged stations at the same depth yielded corresponding discharges for which the discharge ratios were computed and the overall mean ratio of 9:100 (or 1:11.11) was generated. That is, 1m³/s flow in Taylor creek is equivalent of 11.11m³/s flow in River Niger.
2. Similarly, the rainfall intensity-duration-frequency (IDF models) of Port Harcourt city were transposed to an equivalent value for Peremabiri all in Niger Delta. The individual ratios of the annual rainfall totals for Port Harcourt and Peremabiri were computed; the overall average ratio of 1:1.2 was obtained. In effect the factor 1.2 was applied to all the IDF models of Port Harcourt to generate corresponding equivalents for Peremabiri.
3. The hydrologic transposition by ratio approach has been applied to both stream flow and rainfall records from gauged stations to ungauged stations with an overriding condition of similar terrain and meteorological conditions to minimize error. We expect that the ratio approach, though is new and expected to be tested for more hydrological catchment areas to prove its worth and this is the challenge for researchers in hydrology.

None.

The authors of this article have declared that no conflict interests exist in the course of preparing this document.

1. Sehreiner LC, Riedel JT. Probable Maximum Precipitation Estimates, United States East of the 105^th Meridian. US Department of Commerce, National Oceanic and Atmospheric Administration. Hydro Meteorological Report No. 51. 1978;1‒100.
2. Foufoula GE. Probabilistic Storm Transposition Approach for Estimating Exceedance Probabilities of Extreme Precepitation Depth. Water Resour Res. 1989;25(5):700‒815.
3. Portela MM. Hydrology. In: Ramos H, editor. Guidelines for the design of small hydropower plants, Ireland: Cehidro/Wrean/Ded. 2000;21‒38.
4. Alberta Transportation. Guideline on Extreme Flood Analysis. Transportation and Civil Engineering Division, Civil Projects Branch. 2004;1‒112.
5. England JF, Julien PY, Velleux ML. Physically-based extreme flood frequency with stochastic storm transposition and paleoflood data on large watersheds. Journal of Hydrology. 2014;510:228‒245.
6. Gan KC, McMahon TA, O’Neil IC. Transposition of Monthly Streamflow Data to Ungauged Catchment. Hydrology Reseach. 1991;22(2):109‒122.
7. NIWA. Nigerian Inland Waterways Authority. Hydrological year-books compiled by NIWA, lokoja Nigeria. 2012.
8. BS 3680-3B. Measurement of Liquid flow in Open Channels. Stream flow measurement. Guide for establishment and operation of a gauging station. 1977.
9. BS ISO. Measurement of Liquid flow in Open Channels. Determination of Stage Discharge Relation. 1998.
10. Rao AR, Hamed KH. Flood Frequency Analysis. CRC Press LLC. 2000. p. 376.
11. Nwaogazie IL. Probability and Statistics for Science and Engineering Practice. 1st ed. Lagos: Prints Konzults; 2011. p. 252.
12. Nwaogazie IL. Probability and Statistics for Science and Engineering Practice. 2nd ed. University of Port Harcourt Press. 1999. p. 293.
13. Nwaogazie IL. Probability and Statistics for Science and Engineering Practice. 3rd ed. De-Adroit Innovation, Enugu, 2006. p. 302.
14. Ologhadien Itolima, Nwaogazie Ify L. Rainfall-Intensity-Duration-Frequency Models for selected Cities in Southern Nigeria. Standard Scientific Research and Essays. 2014;2(10):509‒515.