The study area comprising parts of upper South Koel river basin, delineated on the Survey of India topographical (SOI) map of scale 1:50000 were updated using LISS III satellite data having resolution 23.5meter (Table 1) IRS-P6 LISS-III satellite data interpretated to demarcate various land use/land cover map and geology map of study area and digitized using Arc-GIS 10.2 software to compute the area under each class. Soil map of the watershed obtained from the National Bureau of Soil Survey (NBSS) was used to create database on the hydrological soil group (HSG). Slope and relief map is prepaired by using cartosat DEM data using Arc-GIS tool box option. Curve numbers (CN) for each soil type required to be assigned for the assessment of run-off. As CN depends on soil type, therefore, on the basis of drainage condition, water transmission capacity ,infiltration rate, texture, depth and the soil was categorized into different HSGs: A, B, C and D. The criteria adopted for such classification of HSGs is based on the USDA-SCS⁴ method. The SCS model computes run-off through an empirical equation and to require rainfall (antecedent soil moisture condition), land cover, soil and the curve number (CN), which represents the run-off prospective of the land cover soil complex.⁸ To calculate the run-off available from the selected watershed using the NRCS soil conservation services (SCS) curve number method, the monthly rainfall data for five years (2009-2013) of monsoon season was acquired from the Indian Meteorological department. The model involves the relationship among land cover, hydrologic soil class and antecedent soil moisture to assign curve number.¹⁴ Physical characteristics (LU/LC and soil) of the watershed AMC and recharge capacity of the watershed are basic requirement for determination of curve number method.¹⁵ The indication of moisture used in run-off estimation is selected as AMC-I, AMC-II and AMC-III which represent dry, normal and wet conditions, respectively. In the present study, HSG and the thematic maps of land use/land cover were prepared in Arc-GIS software for different sub six watersheds and then spatially intersected to calculate the watershed area under the different hydrological similar units (HSU) for assigning CN values to compute total discharge for different sub watersheds. In upper South Koel river watersheds, mainly two hydrological soil group (HSGs) was classified i.e HSG‘B’, and HSG ‘C’, and the area under each HSG was calculated. The type of soil in HSG‘B’ was coarse loamy and the HSG‘C’ are fine and it covers the maximum portion of the watershed. Same process was applied for sub Watershed I, II, III, IV, V and VI to compute curve number values for individual sub watershed. Once the Curve Number was recognized for different land classes, the weighted curve number for watershed was calculated using equation (1).

 $weighted curve number=\frac{{{\displaystyle {\displaystyle \sum C{N}_1\times a_1+C{N}_2\times a_2+.\dots C{N}_n{a}_n}}}^{\text{}}}{{\displaystyle \sum a}}$(1)

Where $C{N}_1$ = curve number for particular land unit 1
$a_1$= area for that particular land unit 1
$C{N}_n$= curve number for nth land unit of watershed, $a_n$ = area of nth land unit of watershed
$\sum a$= sum of total area.
Potential maximum soil retention (S) was estimated for the watershed based on weighted curve number using Equation (2)

$S=\frac{25,400}{CN}-254$(2)

The SCS curve number is based on basic statements i.e for a single storm event, maximum potential of soil retention is equivalent to the ratio of direct run-off and available rainfall. Subsequent to calculation of potential highest soil retention, the initial abstractions (Ia) were calculated. The initial abstractions (Ia) were considered as water losses. Thus, equation (3) is obtained.

$\frac{P-I_a-Q}{S}=\frac{Q}{P-I_a}$(3)

Thus, value of Q is calculated by using equation (2)

$Q=\frac{{\left(P-I_a\right)}^2}{\left(P-I_a+S\right)}$(4)

To simplify the equation (4), ( $I_a$) initial abstraction is related to potential maximum retention and P> Ia. It was considered that if the storm event is less than the initial abstraction value then there is no run-off available for that rainfall event, and only the storm events higher than the initial abstraction value are considered for the run-off estimation.¹⁶ Hence, for storm events is considered for runoff estimation as compare to initial abstraction because of most advancement for the period of five years. The curve number is different for different antecedent field condition. The initial abstraction (Ia) was taken as 0.2S (AMC-II) in the present study. The initial abstractions (Ia) were calculated for 5 years (2009-2013) on monthly basis (June-October) using Equation (6) for the watershed .Weighted curve number and the potential maximum soil retention (S) were calculated by using Ia values shown in Table 6.The whole process was done for six sub-watersheds of upper South Koel basin along with the composite basin area.

$I_a=0.2 S$  (5)

The same weighted curve number (WCN) was used for run-off estimation accordingly given by Anbazhagan et al.¹⁶ by using AMC-II condition as shown in Equation (6):

$Q=\frac{{(P-0.2S)}^2}{P+0.8S}$(6)

Where Q, Actual direct run-off (mm); P, Total Rainfall (mm); S, Maximum soil retention potential mm, CN, Curve Number

By using Equation (6), run-off was calculated in the upper South koel river basin on a monthly (June to October) basis for the period of 5 years (2009-2013, and then observed run-off was estimated using linear regression equation (equation 7) and by computing all runoff value observed the specific month identify which having high runoff volume of discharge during these monsoon season. The correlation between rainfall and runoff can be estimated by obtaining a linear regression line between these two variables.¹⁷ provided the equation (7) used for regression analysis between run-off (R) and rainfall (P).

$R=aP+b$(7)

Where P, Rainfall (mm); R, Run-off (mm); N, No of sets of Rand P

$r=\frac{N{\displaystyle \sum PR}-({\displaystyle \sum P})({\displaystyle \sum R})}{\sqrt{[N({{\displaystyle \sum P}}^2}-\sqrt{P^2}]\times [N{{\displaystyle \sum R}}^2-{{\displaystyle \sum R}}^2]}$

Where P, Rainfall (mm); R, Run-off (mm); N, No. of sets of R and P

Figure 3 Land use land cover classes of upper South Koel river basin Jharkhand.

Figure 4 Soil map of study area (Source–NBSS).

Figure 5 Geology map of study area.

Figure 6 Correlation between rainfall and run-off.

Figure 7 Graphs showing correlation between run-off and rainfall for the monsoon months (June, July, August, September and October) calculated for a period of 5 years (2009‒2013).

Figure 8 Sub watershed map of upper South Koel river basin.

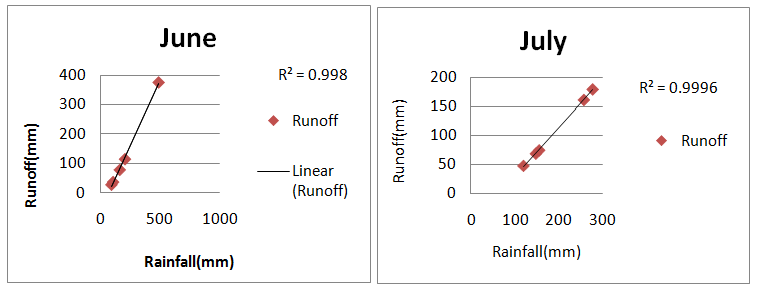
Based on visual interpretation elements viz. color, size, shape, texture and association with standard false color composite of multispectral satellite data of LISS-III nine LULC classes has been identified. The classes and their areal extent obtained as intense agriculture (143.65$k{m}^2$ ), sparse agriculture (148.72 $k{m}^2$ ), Open forest (39.59 $k{m}^2$ ), degraded forest (46.54 $k{m}^2$ ), Reservoir/water bodies (9.24 $k{m}^2$ ), Fallow land (131.47 $k{m}^2$ ), Barren land (91 $k{m}^2$ ), Barren land rocky (80.37 $k{m}^2$ ) and Built up urban /rural areas (81.68 $k{m}^2$ ) as shown Figure 3 & Table 2. Soil map has been taken from NBSS mainly showing three types of soil for an area of 772 i.e Fine loamy, Coarse loamy and Fine soil these three classes further divided into nine classes i.e Fine loamy (Aeric Haplaquents 309.52 $k{m}^2$ ), Coarse loamy (Haplaquents 230.02 $k{m}^2$ ), Fine loamy (Typic Ustochrepts 91.01 $k{m}^2$ ), Fine (Ustrochrepts 11.92 $k{m}^2$ ), Fine loamy(Aeric 11.09 $k{m}^2$ sq), Fine loamy (Haplaustalfs 45.83 $k{m}^2$ ), Fine (Vertic Ustochrepts 53.62 $k{m}^2$ ) shown in Table 3 & Figure 4. Geology map has been also prepaired based on visual interpretation elements of LISS-III satellite data major six types of geological features has been identified in the area as Alluvium (414($k{m}^2$ ), Granite Gneiss (303.4 $k{m}^2$ ), Hornblende Schist & Amphibolite (24 $k{m}^2$ ), Schist (26.70 $k{m}^2$ ), metabasic Dykes (1.23 $k{m}^2$ ) and Laterite (3.36 $k{m}^2$ ) (Figure 5). The entire watershed has been divided into six sub-watersheds based on drainage map prepaired by using toposheet of scale 1:50,000 (SOI) (Figure 8) i.e sub-watersheds I, II, III, IV, V and VI each sub-watershed having nine LULC classes the different classes and their areal extent shown in Table 4 & Figure 8. As curve number values lies between 0-100, the highest curve number obtained 82 for intense agriculture and minimum curve number value is 0 for water bodies and 61 for fallow land 68 for built-up area as shown (Table 5). Based on different hydrological soil group, hydrological condition and land treatment practice CN values for each class is determined. The weighted curve number is calculated for individual sub-watersheds using equation (1) i.e 65, 70, 67.60, 70.19, 67.70 and 67.50 for sub watershed I, II, III, IV, V and VI respectively (Table 7 & 8). Initial abstraction and soil retention is calculated for sub-watersheds based on different CN values obtained using equation (2 and 5) as shown Table 5 & Table 6.Rainfall data of five years from 2009 to 2013 for monsoon season (June-October) taken from Indian Metrological Department is used for computation of runoff using equation (6) which required precipitation data, maximum soil retention and Curve number. The quantity of water discharge from stream is considered as runoff. The average runoff volume estimated from watershed during 2009-2013 for monsoon season was found to be 2880.98 mm generated from 4855mm of rainfall i.e 59% and showing (53, 59, 55, 59, 56 and 57)% of runoff respectively. The relationship between rainfall and runoff volume for five years was examined and plotted (Figure 6) (Figure 7). The result shows high degree of positive co-relation i.e with an increase in rainfall the runoff volume increases. The coefficient of determination was found to be 0.9 for the month (June- October) for different years of observation. The runoff discharge volume has been observed high in the month of August i.e 881.34 mm of runoff in 1388.4 mm of rainfall data for monsoon period of five years from June-October (Table 9).

The average run-off volume estimated from the watershed was found to be 2880.98 mm generated from 4855 mm of rainfall in the upper South Koel basin i.e 59 percent of water is goes as runoff and only 41percent is infiltrate and recharge ground water. The agriculture area covers most part of the watershed (143.65$k{m}^2$ intense agriculture and 148.72 $k{m}^2$  sparse agriculture) having undulating slope and topography which results in the maximum portion of rainwater to escape as run-off and reduces water percolation and infiltration capacity which affect agricultural growth and cause drought condition. The less infiltration and more run-off is also because maximum portion of the watershed is underlain by fine (Aeric Haplaquents) soil (309.52 $k{m}^2$ ) which has a slow water transmission and infiltration rate. Slope distribution is essential parameter as it plays a significant role in determining infiltration vs. runoff relation. Infiltration is inversely related to slope i.e. gentler is the slope, higher is infiltration and less is run- off and vice-versa. Geologic structures have great control as they influence the nature of flow, erosion and sediment transportation. Hard granitic rocks in the basement under shallow soil cover and weathered zone in the study area allows less water to percolate down to the aquifers and therefore major component of rainwater escapes as run-off, thus a large amount of rainwater is vanished as run-off resultant into higher total run-off volume per year causing ground water level depletion in the region of the order of 2.5m per year (CGWB). The geology, extent and type of vegetation cover determines to a large extent the infiltration capacity of the soil and hence the run-off volume.¹ Watershed is divided into major six sub- watersheds i.e sub-watersheds (I,II,III,IV,V and VI) having runoff (53,59,55,59,56,57)% respectively in which sub-watersheds II and IV having high runoff i.e 59% covered with fallow land as the major class (10.29 and 29.96 respectively) and comprised of fine loamy (Typic Ustochrepts) soil and relief is in between 615-650 m because of high runoff in these areas agricultural land may be converted into fallow land. These sub-watersheds must required proper implementation plan to reduce runoff and increase ground water prospect as hydrological harvesting structure construction such as farm ponds, check dams and nala bunds etc in future to combat drought. Coefficient of determination was found to be 0.9 for the months (June-October) for different years of observation which shows high degree of positive correlation i.e with an increase in rainfall, the total runoff volume increases. The resulted observed run-off estimation using SCS-CN is validated with the observed run-off in different studies. Tejram et al.¹⁸ estimated good correlation between rainfall and run-off of the Uri river watershed in the lower Narmada basin of Central India using SCS-CN model. The present study also shows similar type of result and exhibit a good correlation between observed rainfall and run-off.¹⁹ Also estimated total runoff of Jharkhand covering Ranchi and Lohardagga district having rainfall of 1400mm per year and remarked that 60% goes as runoff and only 40% infiltrate and recharge ground source of water. Our study also shows that in Lohardagga district comprising a part of watershed covering an area of about 772 sq km having 2880.98mm of runoff out of 4855 mm of monsoon rainfall i.e 59% of water goes as runoff and about 41% infiltrate and recharge ground water, validating present runoff computation for study area.^20‒23

The present study accurately estimated the total run-off generated in the upper South Koel watershed. Estimation over six sub watersheds helped to quantify the total amount of run-off expected from the individual watershed annually so that runoff could be stored in the suitable recharge structures. The rainfall-run-off modeling using the SCS-CN method showed that the run-off generated in the basin is high over the past 5 years with 2880 mm of runoff generated from 4855 mm of rainfall recorded during the monsoon season (June-October) in which sub watershed II and IV showing high runoff. This entails setting up of various water harvesting structures as per prioritization based on high runoff area, ground water deficit zone considering various drainage morphometric parameters. Less availability of water for domestic and drinking purposes entails building recharge structures to store the run-off water and to provide life saving irrigation facility during agricultural drought as well recharging of aquifers in the watershed.

None.

Authors declare there is no conflict of interest in publishing the article.

1. Tripathi RP, Singh HP. Soil erosion and conservation. New Age International Limited Publication, India; 2001. p. 1‒210.
2. Gupta PK, Panigrahy S, Parihar JS. Impact of Climate Change on Runoff of the Major River Basins of India Using Global Circulation Model (HadCM3) Projected Data. Journal of the Indian Society of Remote Sensing. 2011;39:337−339.
3. Sarangi A, Madramootoo CA, Enright P, et al. Performance evaluation of ANN and geomorphology based models for runoff and sediment yield prediction for a Canadian watershed. Current Science. 2005;89(12):2022‒2033.
4. Soil Conservation Service. Hydrology. National Engineering Handbook, USA; 1985.
5. Srinivas D, Sivaprasad V, Narsimham ML, Ranganna G. Velocity of modified US, SCS method for forested catchments in Sitamadi basin, Karnataka India. Journal of Applied Hydrology.1996.
6. Hariprasad V, Chakraborti AK. Management of small watersheds using hydrologic modeling and GIS. International Conference on Remote Sensing and GIS/GPS. 1997;16−19.
7. Nayak TR, Jaiswal RK. Rainfall-runoff modelling using satellite data and GIS for Bebas River in Madhya Pradesh. IE (I) Journal 2003;84:47‒50.
8. Soil Conservation Service. Hydrology. National Engineering Handbook, USA; 1972. p. 1−127.
9. Chatterjee C, Jha R, Lohani AK, et al. Runoff curve number estimation for a basin using remote sensing and GIS. Asian Pacific Remote Sensing and GIS Journal. 2001;14:1‒7.
10. Bhuyan SJ, Mankin KR, Koelliker JK. Watershed scale AMC selection for hydrologic modeling. Transactions of ASAE. 2003;46(2):303−310.
11. Bhuyan SJ, Koelliker JK, Barnes PL. Modification of curve number adjustment technique for prediction of runoff. In: Ascough IIJC & Flanagan DC, editors. Presented in Soil Erosion Research for the 21st Century, Proceedings of the International Symposium, USA; 2001. p. 1‒290.
12. Pandey A, Sahu AK. Generation of curve number using remote sensing and geographic information system. Water Resources. India; 2002.
13. Pandey A, Pandey S, Nathawat MS. Drought hazard assessment using geoinformatics over parts of Chotanagpur plateau region, Jharkhand, India. Natural Hazards. 2012;63(2):279−303.
14. Gupta PK, Panigrahy S. Geo-spatial modeling of runoff of large land mass: analysis, Approach and results for major river basins of India. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Science. 2008;37:1‒6.
15. Jasrotia AS, Dhiman SD, Aggarwal SP. Rainfall-Runoff and Soil Erosion Modeling using Remote Sensing and GIS Technique- A Case Study of Tons Watershed. Journal of the Indian Society of Remote Sensing. 2002;30(3):167−180.
16. Anbazhagan S, Ramasamy SM, Das GS. Remote sensing and GIS for artificial recharge study, runoff estimation and planning in Ayyar basin, Tamil Nadu, India. Environmental Geology. 2005;48(2):158‒170.
17. Subramanya S. Engineering Hydrology, Tata McGraw-Hill Publishing Company Limited, India; 2006. p. 1−148.
18. Tejram N, Verma MK, Hema BS. SCS curve number method in Narmada basin. International Journal of Geomatics and Geosciences. 2012;3(1):219‒228.
19. Hazra M, Avishek K. Water resources evaluation through water accounting. A means to achieve sustainable development .J Life science. 2010;1:43−50.
20. Jacobs JH, Srinivasan R. Effects of curve number modification on runoff estimation using WSR-88D rainfall data in Texas watersheds. Journal of Soil and Water Conservation. 2005;60(5):274‒279.
21. Pravin R, Kumar U. Geomorphometric Characterization of Upper South Koel Basin, Jharkhand: A Remote Sensing & GIS Approach. Journal of Water Resource and Protection. 2012;4(12):1042−1050.
22. Patil JP, Sarangi A, Singh AK, et al. Evaluation of modified CN methods for watershed runoff estimation using a GIS-based interface. Biosystems Engineering. 2008;100(1):137‒146.
23. Tripathy MP, Panda RK, Pradhan S, et al. Runoff Modelling of a Small Watershed Using Satellite Data and GIS. Journal of the Indian Society of Remote Sensing. 2002;30(1−2):39−52.