In this study bean pod red cargamanto (BPRC) was evaluated as biosorbent for removal of cadmium (Cd²⁺) in aqueous solutions, with the characterization of the material, it was determined that the BPRC is mainly acidic and has functional groups on its surface which provide the ability to adsorb metal ions such as cadmium (Cd²⁺). The effect of pH and Cd²⁺ concentration on biosorption was analyzed. It was found that the optimal conditions for the process are pH 8 and 100 mg L^-1 of Cd²⁺. From the optimal conditions found, it was determined that the material has an adsorption capacity of 0.070 meq g^-1 (3.907 mg g^-1) of Cadmium (Cd²⁺), with a removal percentage of 78.1%. In the biosorption equilibrium, the best fit was a Freundlich isotherm with an intensity (n) of 2.547 and a correlation coefficient R² of 0.980. Kinetic behavior analysis showed the process reaches steady state within 30 minutes of contact. The fit of the experimental data indicates that the pseudo second order model is one of the most accurately describes the results. The kinetic coefficient (K₂) obtained for the model presented a value 1.135 g meq^-1 min^-1 for a correlation coefficient value of 0.999.

Keywords: adsorption, cadmium (Cd²⁺), bean pod red cargamanto (BPRC)

The presence of heavy metals in water due to natural and anthropogenic sources is a problem of great socio-environmental importance. Particularly, cadmium is a non-essential metal, which tends to be accumulated by living beings, for which it is toxic.¹ Its ingestion in minimum concentrations produces effects that go from irritation of the stomach to diseases like cancer. The procedures used for the removal of heavy metals in aqueous solutions generally include distillation, coagulation, flocculation, ion exchange, reverse osmosis, electrodialysis, precipitation, adsorption and nanofiltration.² These technologies present limitations that include high cost, low water recovery, special handling techniques and high volume of secondary waste.³ Adsorption is quite effective, but the most widely used adsorbents (such as activated carbon) present limitations with respect to their high costs. Therefore the technology known as Biosorption has been shown to be quite promising in the removal of contaminants from aqueous effluents.³ Agricultural waste materials may have potential to be used as low cost adsorbents because they represent unused resources that are widely available and are environmentally friendly.⁴ The sorption capacity of these materials is derived from their constituent polymers (cellulose, hemicellulose and lignin) and structure, in which an affinity for the metal ions is manifested.⁵ At the global level, in the removal of heavy metals in aqueous media, various agricultural waste materials such as fruit peels, seeds and natural fibers^6,7 have been explored. For the removal of Cadmium (Cd²⁺), residues such as corn cobs,⁸ rice husks,⁹ wheat stalks¹⁰ and others have been used. According to the characteristics described above and complying with the seventh principle of green chemistry: use of renewable raw materials,¹¹ we seek agricultural waste material generated in large quantities without being used. As a result it is found that the BPRC is typically disposed as waste in landfills or incinerators. It is therefore understood that this material is being wasted without exploring its application in the agricultural sector or in the waste water treatment.

Adequacy of biosorbent

The BPRC belonging to the bush variety was purchased in a market square located in Bogota D.C. Initially this material was dried in the sun, crushed in the mill of IKA universalmühle M20 and sieved. The particle size used in this study corresponds to less than 425 microns. This procedure is performed because the particle size has a significant influence on the biosorption kinetics. Crushing the material increases its contact area or surface development,¹² and this may contribute to a greater retention of the sorbate.

Solutions and reagents

A stock solution of cadmium (Cd²⁺) was prepared from cadmium chloride (CdCl_2·2.5 H₂O) supplied by the brand Baker. In both the preparation of the stock solution and in the different experiments, dilutions were made with ultrapure water obtained in an ELGA Purelab Option. The water obtained has a conductivity <2 μS/cm. HCl (0.1N) and NaOH (0.1N) were prepared. The reagents used for the preparation of the solutions were supplied by the MERCK brand.

Characterization of BPRC

Scanning electron microscopy (SEM) was performed on a TESCAN Model VEGA 3 microscope. The titration to determine the active sites was performed with the Titrino Plus Metrohm 877 automatic titrator¹³ and the Fourier Transform Infrared (FTIR) spectral analysis was performed on the SHIMADZU IRPrestige-21 Spectrometer with a range of 400-4000cm^-1.

Adsorption experiments

The experiments for this project were carried out by the batch method of contacting the biosorbent with the aqueous solution containing the metal, maintaining a homogeneous mixture under agitation to promote adsorption, and then performing the separation by filtration for further analysis.² The pH in the different experiments was measured with a Handylab pH11 SCHOTT potentiometer. The agitation processes were carried out on a KASAI Heidolph plate with temperature, time and velocity control, and the cadmium (Cd²⁺) analyses were performed on the Perkin Elmer AAnalyst 300 Atomic Absorption Spectrometer by the Direct Method of air- Acetylene.¹⁴

The adsorption of the metal by biosorbent is determined by the mass balance equation^15,16

${\text{q}}_{\text{e}}\text{ =V}\frac{\left({\text{C}}_{\text{o }}{\text{- C}}_{\text{e}}\right)}{\text{m}}$ (1)

where ${\text{q}}_{\text{e}}$ , is the amount of metal adsorbed at equilibrium (meq of metal / g dry weight of adsorbent material); $\text{V}$ , corresponds to the volume of the solution (batch) with the biosorbent (L); ${\text{C}}_{\text{o}}$ and ${\text{C}}_{\text{e}}$ correspond to the initial and final concentration of the metal in the solution (meq L^-1>) and m , corresponds to the mass of dry biosorbent added (g). To calculate the percentage of sorbate removal, Re(%) ^16,17 we consider the ${\text{C}}_{\text{r}}$ (Cr=Ce) which is the residual concentration of the sorbate in the solution (mg L^-1):

$\text{Re(\%) =}\frac{\left({\text{C}}_{\text{o}} {\text{- C}}_{\text{r}}\right)}{{\text{C}}_{\text{o}}}\text{100\%}$ (2)

Adsorption isotherms

The distribution of the metal ions in the biosorbent and the metal solution, when the system is in equilibrium, is important in determining the maximum adsorption capacity of the biosorbent. The adsorption and affinity capacity between the biosorbent active sites and the metal ions (indicated by the constants of each model) is analyzed or represented by means of isothermal models. For the present study we chose the Freundlich and Langmuir equations that correspond to the most used models.

Freundlich's general equation^18,19 has the form:

${\text{q}}_{\text{e}}{\text{ = K}}_{\text{f }}{\text{C}}_e^{\frac{1}{n}}$ (3)

Where ${\text{q}}_{\text{e}}$ , is the amount of metal adsorbed at equilibrium (meq of metal / g dry weight of adsorbent material); ${\text{C}}_{\text{e}}$ represents the concentration of the metal remaining in the solution (mg L^-1) and ${\text{K}}_{\text{f }}$ and $\text{n}$ are empirical constants.

The biosorption capacity ${\text{K}}_{\text{f }}$ (meq g^-1), and the intensity ("n" ) are calculated from the intersection and slope of the Freundlich isotherm respectively and these represent the highest efficiency of biosorbent sorption. The linear form of the Freundlich equation is:

${\text{logq}}_{\text{e}}{\text{=logK}}_{\text{f }}\text{+ }\frac{\text{1}}{\text{n }}{\text{ logC}}_{\text{e}}$ (4)

Langmuir equation10,20 has the general form:

$\text{q = }\frac{{\text{ b q}}_{\text{e}}{\text{ C}}_{\text{e}}}{{\text{1 + b C}}_{\text{e}}}$ (5)

where C_e represents the equilibrium concentration of the metal remaining in the solution (mg L^-1); q the amount of metal adsorbed at equilibrium and q_e and b are the Langmuir constants related to adsorption capacity (meq g^-1) and adsorption energy (L meq^-1), respectively.

The values for q_e and b are determined from the slope and intersection of the Langmuir isotherm, respectively. The linear form is:

$\frac{{\text{C}}_{\text{e}}}{\text{q}}\text{ = }\frac{\text{1}}{{\text{q}}_{\text{e}}\text{ b}}\text{ + }\frac{{\text{C}}_{\text{e}}}{{\text{q}}_{\text{e}}}$ (6)

Adsorption kinetic behavior

Kinetic analyses are performed to determine the rate at which the metal or sorbate is removed from the aqueous solution. The most used models to describe the behavior of adsorption processes are the pseudo first order kinetic model, the pseudo second order model, and the intraparticular diffusion model. For the present study, we used the equations corresponding to these three models.

The pseudo first order model^16,21 is defined by the equation that follows:

$\frac{{\text{dq}}_{\text{t}}}{\text{dt}}{\text{ = k}}_{\text{1 }}\left({\text{q}}_{\text{e }}{\text{- q}}_{\text{t}}\right)$ (7)

where q_e and q_t represent the sorption capacity at equilibrium (meq g^-1) at time t, and k1 is the rate constant (min^-1). Integrating equation (7) gives the linear form of the pseudo first order model:

$\text{log}\left( {\text{q}}_{\text{e}}{\text{- q}}_{\text{t}} \right)\text{ = }\frac{\text{log}\left({\text{q}}_{\text{e}}\right) {\text{- k}}_{\text{1 }}\text{ t}}{\text{2}\text{.303}}$ (8)

The pseudo second order mode^19,22 is mathematically defined through the following expression:

$\frac{{\text{dq}}_{\text{t}}}{\text{dt}}{\text{ = k}}_{\text{2}}{\left({\text{q}}_{\text{e }}{\text{- q}}_{\text{t }}\right)}^{\text{2}}$ (9)

Its linear form is:

$\frac{\text{t}}{{\text{q}}_{\text{t}}}\text{ = }\frac{\text{1}}{{\text{k}}_{\text{2}}{\text{ q}}_{\text{e}}{}^{\text{2}}}\text{ + }\frac{\text{t}}{{\text{q}}_{\text{e}}}$ (10)

where q_t represents the amount of adsorbed metal (meq g^-1); t, is the time (min), q_e is the equilibrium adsorption capacity (meq g^-1) and k₂ is the constant of the equation (g meq^-1 min^-1). By plotting t/qt vs t, i.e. the linearized form of the kinetic equation of pseudo second order, the value of k₂ can be obtained from the slope of the straight line obtained.

Finally, the intraparticular diffusion model²³ is mathematically defined by the following equation:

${\text{q}}_{\text{t }}{\text{= k}}_{\text{p }}{\text{ t }}^{\text{0}\text{.5}}\text{+ C}$ (11)

Where Kp (meq g^-1 h^-0.5) represents the intraparticular diffusion rate constant and C is a constant. According to this model, a graph of qt as a function of t^0.5 must be linear if intraparticle diffusion is involved in the adsorption process. The intraparticle diffusion model considers that the velocity of the adsorption process is limited only by intraparticle diffusion if the correlation passes through the origin (C=0), otherwise some other mechanisms besides intraparticular diffusion are participating in the process.²³

Characterization of BPRC

Figure 1 shows the microphotographs of the surface of the BPRC, which show the structure and porosity characteristic of this type of material. In this analysis of the active sites, it was found that the material has acidic characteristics. According to this result and following Boehm,¹³ it could be said that the surface of the BPRC has carboxyl groups (RCOOH), carboxylic acid anhydrides ((RCO)₂O), lactones (RCOOR), lactols (RCOOOH) and phenolic hydroxyl groups (ROH).

Figure 1 Microphotographs of BPRC.

Figure 2 shows the FTIR spectrum of the BPRC. In this Figure it is possible to determine that there is a marked intensity signal at the point 3040 cm^-1, which corresponds to the vibration of the O-H bond, from the lignin. At a frequency of 2638 cm^-1 a symmetric vibration corresponding to the CH₃ bond from the ether of the lignin is also observed. At a frequency of 2030 cm^-1 a weak signal is observed produced by the vibration of the C-O bond of the acetal. At 1380 cm^-1, a band related to the R-CH₃ groups corresponding to the symmetric deformation of the C-H bond is found, and finally a vibration of the O-H bond occurs at a frequency of 1263 cm^-1. The presence of the functional groups determined by the FTIR analysis are those that give the material the ability to adsorb some contaminants. For this specific case the presence of OH groups facilitates the adsorption of metal ions such as cadmium (Cd²⁺).

Figure 2 FTIR spectrum of BPRC.

Adsorption experiments

In order to analyze the influence of pH factors and initial concentration of Cadmium (Cd²⁺) on the efficiency of the biosorption process, an experimental design of composite central type was proposed. The pH of the aqueous solution was adjusted to levels 4 and 8 and the concentration of cadmium (Cd²⁺) in solution was adjusted to values between 50 mg L^-1 and 100 mg L^-1. All experiments were performed in batch mode. Table 1 shows the analysis of variance that indicates the most influential parameters in the process. All factors or interactions among themselves that obtain a probability value P <0.05 (last column of Table 1) are considered the most relevant in the adsorption process. In this case, factors A and B are the most significant.

According to the adjustment, a correlation (R²) of 99.43% was obtained. This value explains the percentage of variables that affect the adsorption capacity of the BPRC. The difference of 0.57 % shows the minimization of possible causes of error. Equation (12) that fitted the model is given by:

$Adsorption capacity \left(q\right)=0.26768+\left(0.032352 pH\right)+\left(0.032091 \left[Cd\right]\right)-\left(5.45\times {10}^{-4} pH \left[Cd\right]\right)+\left(3.35312\times {10}^{-3} p{H}^2\right)+\left(3.746\times {10}^{-5} {\left[Cd\right]}^2\right)$ (12)

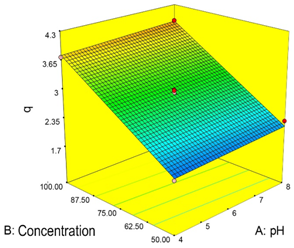
The results obtained in the adsorption capacity evaluation of the BPRC, are summarized in Table 2. Using the model, the response variable (adsorption capacity, q) was optimized. Table 3 summarizes the values of the parameters found by the model to obtain the highest adsorption capacity of cadmium (Cd²⁺) in aqueous solution. The optimal values for the maximization of the response variable are within the study levels previously determined for the experimental design. Figure 3(A) shows the sloped response surface that describes the behavior of the adsorption capacity (q) of Cadmium (Cd²⁺) on the experimental region, and Figure 3(B) shows the different contour lines of the surface. The two variables significantly affect the biosorption process, but the concentration has a greater influence than the pH and this is clear if it is considered that at a higher concentration the driving force for mass transfer becomes greater.

              A                                                        B

Figure 3 (A) Response surface describing the behavior of the adsorption capacity (q) over the experimental region and (B) boundary lines for the adsorption treatment.

Adsorption isotherms

Table 4 presents values ​​of the correlation of the experimental data to the linearized forms of the analyzed isotherm models. Based on these correlations, we determined the values ​​of the parameters in each model, as well as the respective correlation coefficient, by which we can determine the isotherm model that best fits the experimental results. The comparison of the correlation coefficient (R²), allows us to determine that the most adjusted adsorption isotherm model was the Freundlich model with an R² of 0.980 versus a value of 0.955 for the Langmuir model. The adjustment to the Freundlich model indicates that the adsorption is carried out by layers, with a heterogeneous distribution of active sites accompanied by the interaction between adsorbed molecules,² which finally leads to the formation of multiple layers on the initial layer Found on the surface of the material. According to the Freundlich isotherm model, the capacity coefficient K_f was determined to be 4.40 mg/g. Also, the adsorption intensity (n) presented a value of 2.55, indicating a favorability in the adsorption process.²⁴

Adsorption kinetic behavior

In the evaluation of the kinetic behavior of cadmium adsorption, it was verified that at 30 minutes of agitation, the BPRC removed 97.6% of the Cadmium (Cd²⁺) present in aqueous solution from an initial concentration of Cadmium (Cd²⁺) of 100 mg L^-1. The data obtained in the evaluation of the kinetic behavior were represented by the pseudo first order, pseudo second order and intra-particular diffusion models. The corresponding data can be seen in Table 5. According to the results presented in Table 5, it can be observed that the highest correlation coefficient or adjustment of the data is presented with the pseudo second order model, for which the correlation coefficient presents a value of 0.999, a value significantly higher than the coefficient obtained for the other two models applied. The result of the adsorption capacity at equilibrium (q_e), presents precision when compared to the capacity obtained in the experimental design. For the experiments carried out, an adsorption capacity of 3.91 mg g^-1 was obtained in the experimental design and at equilibrium a value of 4.40 mg g^-1.

Comparison of the capacity and time of adsorption of some agricultural residual materials

Table 6 shows the adsorption capacity and time of some similar studies. Some studies show higher adsorption capacities than that obtained with BPRC. However, the BPRC has a short equilibrium time which, from the operational point of view, turns out to be convenient.^25‒31

Through the chemical characterization of the material, it was found that BPRC has acidic characteristics. The concentration of acid sites is higher than that of basic sites, which allows cadmium (Cd²⁺) to be fixed on the surface of the BPRC. The FTIR spectrum denotes the presence of functional groups that potentiate the capacity of the BPRC for the removal of Cadmium (Cd²⁺) present in aqueous solution. The pH and concentration factors significantly affect the biosorption process. However, the results of the experimental tests indicate that concentration has a greater influence if it is considered that when the concentration increases, the driving force for mass transfer increases. The experiments allowed to determine that the equilibrium of the process can be represented with greater precision through a Freundlich isotherm model. This model typically describes physical adsorption models. The kinetic behavior of the process is characterized by a short adsorption period (between 5 and 30 minutes), from which time it is well known that the concentration of the sorbate tends to stabilize in the aqueous solution in contact with the adsorbent. The experimental data fit the kinetic model of pseudo second order. The adsorption time is efficient compared to other untreated agricultural waste materials which, although reaching adsorption capacities higher than the material analyzed in this study, require longer contact times to achieve process stability.

None.

The authors declare there is no conflict of interest.

1. Unite States, Agency for Toxic Substances and Disease Registry (ATSDR). Toxicological profile for Cadmium. ATSDR; 2012;1–487.
2. Srivastava S, Goyal P. Novel biomaterials. Decontamination of toxic metals from wastewater. Berlin Heidelberg: Springer – Verlag. 2010;147.
3. Demirbas A. Heavy metal adsorption onto agro–based waste materials: A review. Journal of Hazardous Materials. 2008;157(2–3):220–229.
4. Kratochvil D, Volesky B. Advances in the biosorption of heavy metals. Trends in biotechnology. 1998;16(7): 291–300.  
5. Laszlo JA, Dintzis FR. Crop resides as Ion exchange material. Treatment of soybean hull and sugar beet fiber (pulp) with epichlorohydrin to improve cation–exchange capacity and physical stability. Journal of Applied Polymer Science. 1994;52(4):531–538.
6. FebriantoJ. Equilibrium and kinetic studies in adsorption of heavy metals using biosorbent: A summary of recent studies. Journal of Hazardous Materials. 2009;162(2–3):616–645.
7. Sud D, Garima, Mahajan et al. Agricultural waste material as potential adsorbent for sequestering heavy metal ions from aqueous solutions – A review. Bioresource Technology. 2008;99:6017–6027.
8. Leyva Ramos R, Bernal Jacome LA, Acosta Rodriguez. Adsorption of cadmium (II) from aqueous solution on natural and oxidized corncob. Separation Purification Technology. 2005;45:41–49.
9. Upendra Kumar, Manas Bandyopadhyay. Sorption of cadmium from aqueous solution using pretreated rice husk. Bioresource Technology.  2005;97(1):104–109.
10. Tan Guangqun, Xiao Dan. Adsorption of cadmium ion from aqueous solution by ground wheat stems.  Journal of Hazardous Materials. 2008;164(2–3):1359–1363.
11. James Clark, Duncan Macquarrie. Handbook of Green Chemistry And Technology. Oxford: Blackwell Science LTD. 2007.
12. Michell J Sienko, Robert A Plane. Química. Traducido por: Federico Portillo García. Madrid. Aguilar. 1965;641.
13. Boehm HP. Surface oxides on carbon and their analysis: a critical assessment. Carbon. 2002;40(2):145–149.
14. APHA, AWWA, WPCF. Métodos Normalizados para el análisis de aguas potables y residuales. Díaz de Santos SA ediciones. 1992.
15. Hengky, Harmita, Karthikeyan KG, et al. Copper and Cadmium sorption onto Kraft and organosolv lignins. Bioresource Technology. 2009;100(24):6183–6191.
16. Azouaou N. Adsorption of cadmium from aqueous solution onto untreated coffee grounds: Equilibrium, kinetics and thermodynamics. Journal of Hazardous Materials. 2010;184(1–3):126–134.
17. Li Qingzhu, Liyuan Chai, Wenqing Qin. Cadmium (II) adsorption on esterified spent grain: Equilibrium modeling and posible mechanisms. Chemical Engineering Journal. 2012;197:173–180.
18. Zheng L. Equilibrium and kinetic studies of adsorption of Cd (II) from aqueous solution using modified corn stalk. Journal of Hazardous Materials. 2010;176(1–3):650–656.
19. Özer A, Pirincci HB. The adsorption of Cd (II) ions on sulphuric acid–treated wheat bran. Journal of Hazardous Materials. 2006;137(2):849–855.
20. Al–Anber ZA, Mohammed Abu DM. Batch adsorption of cadmium ions from aqueous solution by means of olive cake. Journal of Hazardous Materials. 2008;151(1):194–201.
21. Akl M Awwad, Nidá M Salem. Kinetics and thermodynamics of Cd (II) biosorption onto loquat (Eriobotrya japonica) leaves. Journal of Saudi Chemical Society. 2011;18(5):486–493.
22. Eun Woo, Shin KG, Karthikeyan, et al. Adsorption mechanism of cadmium on juniper bark and wood. Bioresource technology. 2007;98(3):588–594.
23. Ahmad, Mohd A, Alrozi R. Removal of malachite green dye from aqueous solution using rambutan peel–based activated carbon: Equilibrium, kinetic and thermodynamic studies. Chemical Engineering Journal. 2011;171(2):510–516.
24. Yardim. Removal of mercury (II) from aqueous solution by activated carbón obtained from furfral. Chemosphere. 2003;52(5):835–841.
25. Benaissa H. Screening of new sorbent materials for cadmium removal from aqueous solutions. Journal of Hazardous Materials. 2006;132(2–3):189–195.
26. Nouri L. Batch sorption dynamics and equilibrium for the removal of cadmium ions from aqueous phase using wheat bran. Journal of Hazardous Materials. 2007;149(1):115–125.
27. Ghodbane I. Kinetic and equilibrium study for the sorption of cadmium (II) ions from aqueous phase by eucalyptus bark. Journal of Hazardous Materials. 2008;152(1);148–158.
28. Asma Saeed, Muhammad Iqbal, Wolfgang H. Höll. Kinetics, equilibrium and mechanism of Cd2+ removal from aqueous solution by mungbean husk. Journal of Hazardous Materials. 2009;168(2–3):1467–1475.
29. Singh KK, Singh AK, Hasan SH. Low cost bio–sorbent wheat bran for the removal of cadmium from wastewater: Kinetic and equilibrium studies. Bioresource Technology. 2006;97(8):994–1001.
30. Zheng W. Adsorption removal of cadmium and copper from aqueous solution by areca– A food waste. Journal of Hazardous Materials. 2008;15(2–3):490–495.
31. Bhattacharyya KG, Gupta SS Adsorption of a few heavy metals on natural and modified kaolinite and montmorillonite: A review. Advances in colloid and interface science. 2008;140:114–131.