Evaluation methods for groundwater inflows into rock tunnels: a state-of-the-art review

doi:10.15406/ijh.2021.05.00277

International Journal of

eISSN: 2576-4454

Hydrology

Research Article Volume 5 Issue 4

Evaluation methods for groundwater inflows into rock tunnels: a state-of-the-art review

Wadslin Frenelus,

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Hui Peng, Jingyu Zhang

Department of Hydraulic Engineering, College of Hydraulic and Environmental Engineering, China Three Gorges University, China

Correspondence: Wadslin Frenelus, Department of Hydraulic Engineering, College of Hydraulic and Environmental Engineering, China Three Gorges University, Yichang, Hubei, 443002, China, Tel +86-132-3562-4171

Received: June 24, 2021 | Published: July 13, 2021

Citation: Frenelus W, Peng H, Zhang J. Evaluation methods for groundwater inflows into rock tunnels: a state-of-the-art review. Int J Hydro. 2021;5(4):152-168. DOI: 10.15406/ijh.2021.05.00277

Download PDF

Abstract

Groundwater inflow into tunnels is always a salient topic in Hydrology, Hydraulic Engineering, Hydrogeology, Rock Engineering and allied sciences. In fact, tunnels particularly built below the groundwater table, often face groundwater inflows during their excavation, and even sometimes after they are put into operation. These inflows, habitually regarded as unpredictable geological hazards, cause instabilities in the surrounding rocks of tunnels, and lead to considerable damages such as injuries, loss of lives, and huge-scaled economic expenses. It is argued that groundwater conditions are of decisive significance for the design and running of tunnels. Therefore, accurate prediction or evaluation of groundwater inflows into tunnels is of paramount importance. Such prediction, although it is still challenging, has been broached by many researchers with diverse methods. However, a state-of-the-art review of these methods has not yet been presented. This paper reviews the assessment methods of groundwater inflows into tunnels built in rocky media. The results mainly include analytical, semi-analytical, empirical, semi-empirical, numerical, machine learning, and other methods used in the field. This was made possible by selecting and analysing relevant scientific articles published by various worldwide Journals. In addition, some recommendations and future trends are pointed out. This paper can provide useful references in understanding groundwater inflows prediction in different points of view and their limits in terms of applicability and accuracy.

Keywords: groundwater inflows, groundwater inflows prediction, water table, accurate groundwater inflows prediction, rock behaviors, tunnels stability

Abbreviations

EDZ, excavation damaged zone; EdZ, excavation disturbed zone; TIC, tunnel inflow classification; GSR, groundwater seepage rate; SGR, site groundwater rating; TBM, tunnel boring machine; DB, drill-and-blast; RMR, rock mass rating; VMD, variational mode decomposition; ORELM, outlier robust extreme learning machine; MOGWO, multi-objective grey wolf optimizer; HGWO, hybrid grey wolf optimization; SVR, support vector regression; GIS, geographic information system

Introduction

The assessment or prediction of groundwater inflows is crucial for the design and stability of tunnels, as well as for mitigating associated environmental impacts.^1,2 Adequate planifications are always required prior to excavate deep rock tunnels, particularly those built in saturated media. Due to the growing needs of underground spaces, tunnels are generally designed and built for various purposes such as water conveyance, reservoirs emptying, hydropower stations, sanitary drainage, transport systems, etc. One of the challenge facing designers and builders is controlling the groundwater inflows into tunnels. In fact, the latter can increase the risk of excavations failure by influencing their short and long-term stability.³ Groundwater inflows are generally generated during and after deep tunnels excavation, and they influence the behavior of rocks. More precisely, they induce overall instability and reduce rock strength and shear.⁴ Moreover, the unanticipated high rate of groundwater inflow can engender serious damages like loss of lives and destruction of related equipments.^5,6 For instance, Sammarco⁷ reported that 4 groundwater inrushes resulted in the deaths of 17 people from 1910 to 1964 in the southern Tuscany underground mine of Italy, and more than 1 million of water have been pumped there. On 21 January 2006, a water inrush accident occurred during the construction of Malujing Tunnel (Hubei Province of China), has caused 11 casualties and many injuries.⁸ In China and elsewhere, many casualties and economic loss are caused by hundreds of water inrushes during tunnelling.⁹ More recently, Liu et al.¹⁰ reported that the unexpected groundwater inflows at a tunnel head provoke uncontrollable effects like mechanical instability and environmental impacts. All these situations can explain that proper evaluation of groundwater inflows is highly required for suitable treatment and ensuring the long-term stability of tunnels.

Analysis of the literature shows that many efforts have been made during the past decades to predict and calculate groundwater inflows into rock tunnels. In fact, different methods have been developed for that. They mainly include analytical, semi-analytical, empirical, semi-empirical, and numerical methods. Despite all, owing to various potential factors, it remains a challenging task to accurately assess groundwater inflows into tunnels.¹¹ This is explained by the fact that rock masses are typically complexes and heterogeneous, and it is very difficult to determine accurately their relevant properties. Thereby, assumptions are habitually made in order to simplify pertinent parameters and real features of the rocky media.^11,12 Appropriate selection of one or more methods is also not always obvious, due to the various approaches. This paper aims to provide a review of the assessment methods for groundwater inflows into tunnels built in rocky media. Many studies have been carried out on the prediction of groundwater inflows into underground structures. However, attention has not been drawn sufficiently to the comparison and examination of different methods for assessing groundwater inflows into tunnels. To address this issue, this paper presents a reminder highlighting salient research results published in the field. It provides thus a summarized update of the most relevant researches in the field.

Material and methods

We performed a systematic literature review by selecting relevant scientific articles published by different worldwide journals. Indeed, we only use information derived from salient papers that have been peer-reviewed. During the reviewing, we followed the guidelines proposed by Okoli and Schabram¹³ where literatures can be used at any period of time. The review is mainly structured in two essential parts: results and discussion. The results are extractions of relevant information on groundwater inflows into rock tunnels. In the discussion part, the potential factors and their impacts on the precision of groundwater inflows into tunnels are mainly presented. Then, from the results and the discussion, we conclude and offer some recommendations and future trends.

Results

Definitions and descriptions of groundwater inflows into rock tunnels

A review of literature reveals that many definitions and descriptions are attributed to the groundwater inflows into rock tunnels. They are generally based on various approaches and considerations. Although they have the same objective of predicting the groundwater inflow into tunnels, but it is very important to present the most relevant of them. This could facilitate a better understanding of groundwater inflows into tunnels or into underground excavations. Table 1 presents pertinent definitions and descriptions of groundwater inflows into tunnels or underground excavations provided in the literature.

Authors	Definitions and Descriptions of groundwater inflows into tunnels or excavations
Meiri¹⁴	Defined groundwater inflow into tunnels as one of the first geotechnical issues. Important groundwater inflows are dangerous and impose additional costs and construction delays.
Singh and Reed¹⁵	In mining excavations, groundwater inflow is mostly the results of interaction of 3 potentials factors namely the mining geometry, the groundwater system, and the hydrogeological features of the rock mass.
Cesano et al.¹⁶	Defined groundwater inflows into tunnels as considerable technical and environmental issues for underground constructions.
Molinero et al.¹⁷	In fractured bedrock, groundwater inflows into tunnels are serious hazards and govern the tunnels progress rate.
Lipponen and Airo¹⁸	Defined groundwater inflow as a crucial factor affecting the planning and running of underground structures; inflow and fractures could be likely linked.
Hwang and Lu⁵	During tunnel construction, groundwater inflow is one of the most typical and challenging concern facing designers and builders.
Li et al.¹⁹	Defined groundwater inflow into tunnels as potential danger and major factor affecting the construction schedule.
Jiang et al.²⁰	Defined groundwater inflow (also called groundwater discharge) as potential geological hazards. It may affect the tunnel excavation time and the construction cost.
Font-Capó et al.²¹	TBM reveal that the problems generated by groundwater inflows are attributed to the existence of faults or fractures zones which are hydraulically conductive.
Butscher¹	A considerable matter in tunnel engineering, generating groundwater drawdown and further environmental impacts.
Huang et al.⁶	In practice, groundwater inflows into tunnels are typical hydrogeological problem. Among the factors that affect it, the fractures aperture effects are preponderant in fractured environments.
Holmøy & Nilsen²²	Groundwater inflow into underground constructions may cause various nuisances such as the risk of groundwater drawdown, attenuation of the rock mass stability, etc.
Javadi et al.²³	The inflow of groundwater into excavations is one of the most serious and difficult problems that hydrogeologists face, and it causes many adverse conditions.
Hadi and Homayoon²⁴	It is one of the most considerable problems in excavations operation, generating delayed operations and surrounding rock instabilities, inflicting additional pressure on tunnels supports systems, and additional expenses.
Maleki²⁵	Defined groundwater inflow as one of the utmost risk in completing tunnels projects.
Zabidi et al.¹¹	Groundwater inflows into tunnels are one of the most unpredictable dangers in excavations, and are preponderantly governed by the existence of fault and open fractures.
Wang et al.²⁶	In discontinuous media, excavations perturbations alter the fracture apertures and the groundwater rate distribution into them. Stress field, fractures geotechnical properties and the embedding depth govern the extent of groundwater inflows into underground openings.
Zhang et al.²⁷	In stratified rock masses, groundwater inflow (also called groundwater flowing) into tunnels is ordinarily a challenge for designers, builders and personnel maintenance, can generate further floods and other problems.

Table 1 Definitions and Descriptions of groundwater inflows into tunnels or excavations

Classification of methods for predicting groundwater inflows into rock tunnels

Analysing the literature, methods predicting groundwater inflows into rock tunnels include, up to now, at least analytical, semi-analytical, empirical, semi-empirical, numerical, machine learning, and other methods, as showed in Figure 1.

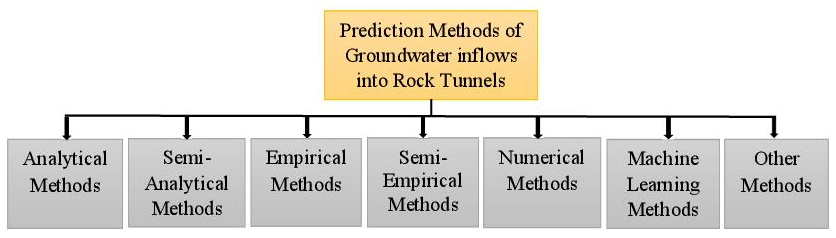
Figure 1 Classification of Methods for predicting Groundwater inflows into rock Tunnels.

Groundwater inflows triggering and mechanisms into rocks tunnels

A good understanding of the triggering steps and the mechanism of groundwater inflows into tunnels is very useful for a better evaluation of said inflows. During tunnels excavations, the surrounding rocks endure a complex unloading-loading process.^28,29 Thus there is redistribution of the existing stress field. Then, two main zones are formed namely the Excavation Damaged Zone (EDZ), and the Excavation Disturbed Zone (EdZ). EDZ is the zone where surrounding rocks deformations are permanent. In fact, the physical, mechanical, hydraulic and geochemical properties of rocks are considerably altered in the EDZ.^30-32 It should also be noted that by excavations, according to the relevant conditions, strain elastic energy can be released;³³ and rockbursts could be generated.^34,35 When the tunnelling takes place below the groundwater table, the stored groundwater is perturbed. Groundwater inflows into tunnels may constitute a response to this perturbation. Normally, their extent depends on several factors associated with the media subjected to stress generated by the excavations. EDZ is a potential factor facilitating the creation of pathway for groundwater inflows into tunnels.³⁶ In fractured rocks, this facilitation increases due to discontinuities. It remains complex to exactly predict flow-paths. Referring to Lianchong et al.³⁷ stress redistribution may generate reactivation of faults zones, and the permeability of these zones are enhanced. Consequently, pathways between fault and damage zones are created for groundwater inflows. By analysing rocks porosity and permeability, Liu et al.³⁸ simulated a safety thickness (Figure 2) of surrounding rocks below which groundwater inflows can occur into tunnels. According to them, when the safety thickness is lower that 4 or 5 m, groundwater inflow evolution has three stages (slowly, mutation and stable stages).

Figure 2 Safety thickness of the rocks surrounding the tunnels, adapted from Liu et al.³⁸

From the excavation of shallow or deep rock mass, the different steps leading to the Triggering of groundwater inflows into rocks Tunnels could be summarized through Figure 3. The mechanism of groundwater inflows into rock tunnels varies depending on the rock masses properties and the relevant conditions. The magnitude of these inflows into tunnels depends on 4 potential factors namely the hydraulic conductivity, availability of groundwater aquifers and storage, permeability of surrounding rocks, and hydraulic gradient.¹⁸ According to Zarei et al.¹² lithology and rock solubility and some fractured rocks can increase rock permeability, since they tend to karstification. The features related to the mechanism of groundwater inflows into rock tunnels are presented in Figure 4. The flow mechanism could be described in Figure 5, according to Sharifzadeh et al.³⁹ For tunnels in sedimentary rock masses and taking into account the Tunnel Inflow Classification (TIC) proposed by Zarei et al.¹² groundwater inflow mechanism can be described as shown in Figure 6.

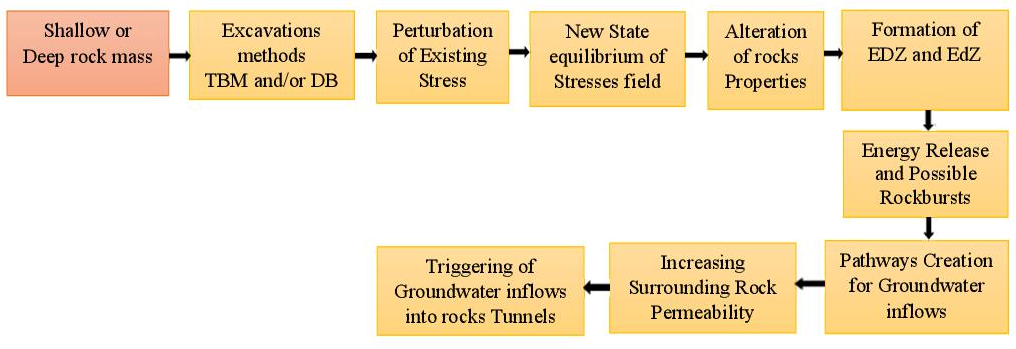
Figure 3 Steps leading to the Triggering of Groundwater inflows into rocks Tunnels.

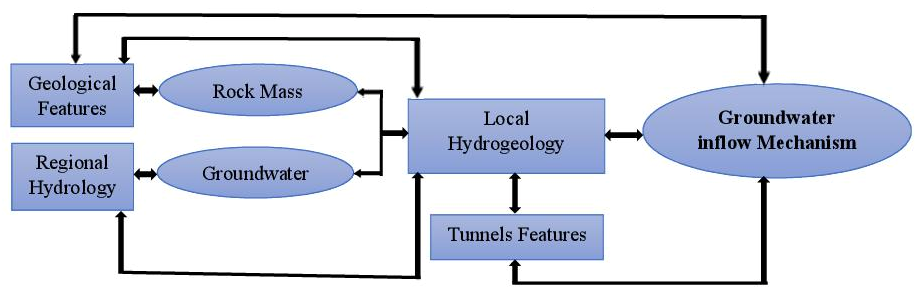
Figure 4 Features related to groundwater inflows into rock tunnels, adapted from Sharifzadeh et al.³⁹

Figure 5 Flow mechanism of groundwater into tunnels with 6 m diameter according to Sharifzadeh et al.³⁹

Figure 6 Description of groundwater inflow mechanism into tunnels, according to Zarei et al.¹²

Relevant analytical and semi-analytical methods

Over years, analytical and semi-analytical methods are widely used to predict groundwater inflows into rock tunnels and into various underground openings. Assumptions and conditions are usually taken into account when establishing analytical and semi-analytical equations. Figure 7 illustrates a circular tunnel in a semi-infinite rock mass with horizontal water table according to Hassani et al.⁴⁰ Its description is habitually used for almost all the aforementioned methods. The main equations resulting from these methods are presented in Table 2.

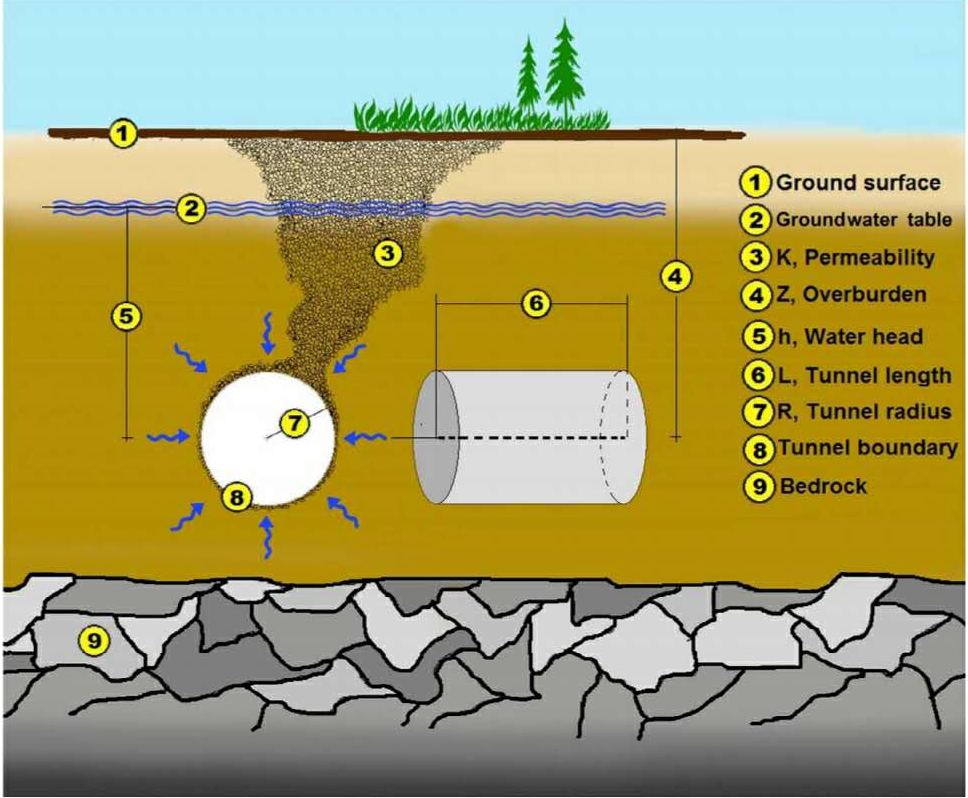
Figure 7 Illustration of circular tunnel in a semi-infinite rock mass with horizontal water table, adapted from.⁴⁰

Governing equations and parameters	Applicability	Remarks	Researchers
$Q = β \frac{2 π K_{3} h_{w}}{\ln (\frac{r_{2}}{r_{3}})}$ $β = \frac{\ln (\frac{r_{2}}{r_{3}})}{- (\frac{k_{3}}{k}) l n R_{0 s} + \frac{k_{3}}{k_{1}} \ln (\frac{r_{1}}{R}) + (\frac{k_{3}}{k_{2}}) \ln (\frac{R}{r_{2}}) + \ln (\frac{r_{2}}{r_{3}})}$	Deep circular tunnels with grouting and lining support. Karst media. Darcy flow	Equations based on Conformal Mapping Technique	Jiang et al.⁴¹
$Q$ : groundwater inflow per unit length; $β$ , Reduction coefficient of lining; $h_{w}$ : water head; $r_{1}$ grouting circle’s radius; $r_{2}$ radius of initial support; $r_{3}$ : secondary lining’s radius; $k_{1}, k_{2}, k_{3}$ : respectively permeability coefficient of grouting circle, initial support and secondary lining; $R$ : Tunnel’s radius.
$Q = \frac{2 π h_{0} K_{1}}{\ln (\frac{r_{1}}{r_{0}}) + \frac{K_{1}}{K_{2}} \ln (\frac{r_{2}}{r_{1}}) + \frac{K_{1}}{K_{3}} \ln (\frac{h_{0}}{r_{2}})}$	Deep circular tunnels with lining and grouting. Homogeneous media. Darcy flow	Different grouting ring thickness considered for treatment	Xu et al.⁴²
$Q$ : groundwater inflow into tunnels $(m^{3} / s)$ : boundary head of the lining; $h_{o}$ : Tunnel diameter; $r_{o}$ : lining diameter; $r_{1}$ : outer diameter of the grouting ring; $r_{2}$ : respectively equivalent hydraulic conductivity of lining; $k_{1}, k_{2}, k_{3}$ Hydraulic conductivity of the grouting area; hydraulic conductivity of surrounding rock.
$Q = \frac{2 π h_{w} k_{s}}{\frac{π}{e^{- α D} \int_{0}^{π} e^{α r c o s θ} d θ} \ln (\frac{2 h}{r_{j}}) + \frac{k_{s}}{k_{j}} \ln (\frac{r_{j}}{r_{l}}) + \frac{k_{s}}{k_{l}} \ln (\frac{r_{l}}{r_{0}})}$	Circular tunnels with grouting and lining. Heterogeneous and isotropic rocky media. Darcy flow	Hydraulic conductivity of the grouting is nonlinear. Grouting and lining are Homogeneous and isotropic.	Cheng et al.⁴³
$Q$ : groundwater inflow per unit length $(m^{3} d^{- 1} m^{- 1})$ ; $α$ : reduction coefficient $(m^{- 1})$ ; D; Center line tunnel depth; $k_{s}$ : hydraulic conductivity at D=0; $k_{j}$ : hydraulic conductivity of the grouting; $k_{l}$ : hydraulic head of the grouting; $θ$ : angle between lengthwise axis and the tunnel radius; $r_{j}$ : grouting outer radius; $r_{l}$ : lining outer radius; $r_{0}$ : lining inner radius; $h$ : groundwater head; $h_{w}$ : groundwater table at early stage of investigation.
$Q = (\begin{matrix} \frac{a_{F} (J 1) \times C (J 1) \times \sin (α_{J 1})}{1000 S_{J 1}} + \\ \frac{a_{F} (J 2) \times C (J 2) \times \sin (α_{J 2})}{1000 S_{J 2}} + \\ \dots + \\ \frac{a_{F} (J 3) \times C (J 3) \times s i n (α_{J 3})}{1000 S_{J n}} \end{matrix}) k h L_{e}$	Deep circular tunnel. Jointed rocks media. Darcy flow	Geological and Hydraulic parameters, as well as tunnel properties are required. The equations are derived from the Groundwater Seepage Rating (SGR).	Maleki²⁵
$Q$ : Effective groundwater inflow into tunnel $(m^{3} d^{- 1} m^{- 1})$ ;: joints aperture (mm); $α_{J}$ : joint aperture surface $m^{2}$ ; $C (J)$ Shape perimeter from joint strike intersection and tunnel axis (m); $S (J)$ : joints spacing (m); $h$ : water head (m); $J_{1} ..., J_{2}, J_{n}$ : joints sets. $k$ : hydraulic conductivity (m/s); $L_{e}$ : effective discharge length (m).
	Circular lined Tunnel. Homogeneous media. Isotropic permeability. Constant water table. Darcy flow	Semi-analytical equations derived from Conformal mapping and Fourier series	Ying et al.⁴⁴
$Q$ : Groundwater inflow into tunnel $(m^{3} d^{- 1} m^{- 1})$ ; $k_{s}$ : aquifer permeability coefficient (m/s); $C_{1}$ : parameter derived from conformal mapping and Fourier series.
$Q = 2 π k \frac{{0.3 (\frac{r}{h})}^{- 0.014 r - 0.22} h}{l n \frac{2 h}{r}}$	Circular tunnel, Homogeneous media.	Consideration on the effects of excavation- induced drawdown.	Su et al.²
$Q$ : groundwater inflow into tunnel (L/min/m); $k$ : hydraulic conductivity; $h$ : initial piezometric head above the tunnel center; $r$ : radius of tunnel.	Isotropic permeability. Darcy flow
$Q = \frac{- \frac{a}{2 π} l n \frac{r}{2 h} - \frac{1}{2 π} \sqrt{{(a l n \frac{r}{2 h})}^{2} - 4 b h (\frac{l n 2 h}{2 h} - \frac{l n r}{r})}}{\frac{b}{2 π^{2}} (\frac{l n 2 h}{2 h} - \frac{l n r}{r})}$	Circular tunnel, homogeneous media. Non-Darcy flow	Atkinson equations are used to determine the experimental constants a, b.	Joo & Shin⁴⁵
$Q$ : groundwater inflow into tunnel; $r$ : Tunnel radius; $h$ : initial piezometric head above the tunnel center; $a, b$ : parameters
$Q = k (S + C) H$	Deep Horseshoe Tunnels and Cavern (subsea). Homogeneous and isotropic rocky media. Darcy flow.	Semi-analytical equations. Mass conservation is considered.	Xu et al.⁴⁶
$Q$ : Groundwater flow into tunnel; $S$ : coefficient linked to the shape and depth of tunnel; $C$ : another coefficient linked to the shape and depth; $k$ : hydraulic conductivity; $H$ : Water head at the upper limit.
$Q = 2 π K \frac{e^{- 2 b h}}{a} \frac{I_{0} (b r) - I_{0} ((b + a γ_{w}) r) e^{- a γ_{w} h}}{K_{0} (b r) - I_{0} (b r) K_{0} (2 b h)}$	Circular tunnels. Heterogeneous media with different behaviors. Darcy flow	Transient consolidation is considered. Integral solution technique is employed.	El Tani⁴⁷
$Q$ : groundwater inflow into tunnel, $k$ : hydraulic conductivity; $a, b$ : constant parameter; $h$ : piezometric head above the tunnel centre; $r$ : tunnel radius; $γ_{w}$ : specific water height; $K_{0}$ : modified Bessel function for the 2nd kind of order zero; $I_{0}$ : modified Bessel function for the 1st kind of order zero.
$Q = \frac{2 π K (H - h_{a})}{l o g \frac{h_{1} + \sqrt{h_{1}^{2} - r^{2}}}{r}}$	Circular deep and shallow tunnels, homogeneous media. Isotropic permeability. Darcy flow	Conformal mapping Technique is the basis of this equation. Water table is constant.	Kolymbas & Wagner⁴⁸
$Q$ : Groundwater inflow per m of tunnel length; $k$ : Isotropic permeability coefficient; $h_{1}$ : piezometric head above the tunnel center; $h_{α}$ : energy head of the tunnel drained perimeter; $H$ : distance from the ground surface and the head of water table; $r$ : tunnel radius.
$Q = 2 π \sum_{i = 1}^{N} h (t - t_{i}) \times \int_{0}^{υ (t - t_{i})} \frac{K_{i} s_{i} H (L_{i} - x)}{\ln [1 + \sqrt{\frac{π K_{i}}{S_{i} r_{i}^{2}}} (t - t_{i} - \frac{x}{υ_{i}})]} d x$	Drilled tunnel, heterogeneous media. Transient flow. Non-Darcy flow	Equations derived by convolution and superposition principles. Consecutive sectors are considered.	Perrochet & Dematteis⁴⁹
$Q$ : Total groundwater inflow into tunnel (L/s); $r_{i}$ : tunnel radius; $H$ : Heaviside step-function ( $H (u) = 1$ if $u > 0$ ; $H (u) = 0$ ,if: $u < 0$ ) drilling speed; $υ_{i}$ : drilled speed at sector: $i$ ; $t$ time; $t_{i}$ : time of sector: $i; x :$ coordinate along the tunnel axis; $K_{i}$ : hydraulic conductivity; $S_{i}$ : Specific storage coefficient; $S_{i}$ : Thickness of saturated zone; $L_{i}$ : length at a sector
$Q = {\begin{matrix} \frac{F (α)}{L_{α_{d}}}, α < α_{d} \\ \frac{F (α)}{L_{α_{d}}} - \frac{F (α - α_{d})}{L_{α_{d}}}, α > α_{d} \end{matrix}$ $F (α) = \frac{2}{π} (E i (2 \ln (1 + \sqrt{π α})) - E i (\ln (1 + \sqrt{π α})) - \ln (2))$	Circular tunnels. Homogeneous media. Transient flow is considered. Darcy flow	Progressive drilling excavation. Equations derived by a development of convolution integral.	Perrochet⁵⁰
$Q$ : dimensionless groundwater discharge into tunnel; $α_{d}$ : dimensionless drilling times; $α$ : dimensionless time; $E i$ : exponential integral function; $L_{α_{d}}$ : distance or length measured at a drilling time $α_{d} .$
$Q = 2 π k \frac{λ^{2} - 1}{λ^{2} + 1} \frac{h}{l n λ}$ $Q = 2 π k \frac{λ^{2} - 1 + c {(λ - 1)}^{2}}{λ^{2} + 1} \frac{h}{l n λ}$ $λ = \frac{h}{r} - \sqrt{\frac{h^{2}}{r^{2}} - 1}$	Circular tunnels with lining, homogeneous media. Darcy flow	The first equation is designed without the lining effect. The second takes account of the lining effect.	El Tani⁵¹
$Q$ : groundwater inflow into tunnel ( $m^{3} . s^{- 1} m^{- 1}$ ): piezometric head above the tunnel centre; $k$ : hydraulic conductivity (m/s); $r$ : tunnel radius (m); $λ$ : a parameter; $c$ : a proportionality coefficient.
$Q = 2 π K h \frac{1 - 3 {(\frac{r}{2 h})}^{2}}{[1 - {(\frac{r}{2 h})}^{2}] l n \frac{2 h}{r} - {(\frac{r}{2 h})}^{2}}$	Square, Elliptical or Circular tunnels. Varied hydraulic conductivity. Darcy flow.	Fourier series is the basis of this equation	El Tani⁵²
$Q$ : groundwater inflow into tunnel; $h$ : depth from the tunnel’s center line and the water head; $k$ : hydraulic conductivity; $r$ : tunnel radius.
$Q = 2 π K \frac{h}{\ln [\frac{h}{r} + \sqrt{\frac{h^{2}}{r^{2}}} - 1]}$	Circular tunnels, homogeneous media. Darcy flow	Total constant water head around the tunnel is considered.	Lei⁵³
$Q$ : Tunnel inflow per unit length; $K$ : hydraulic conductivity of the media; $r$ : tunnel radius; $h$ : depth from the tunnel’s center line and the water head.
$Q = \frac{2 π K e x p [- (A + a_{1}) L] [\exp (a_{1} h) - 1]}{a_{1} [K_{0} (\frac{A}{4} d) - K_{0} (A L)]}$	Deep circular tunnel. Heterogeneous media. Hydraulic conductivity gradient varied with depth. Darcy flow	Equation derived from mirror method	Zhang and Franklin⁵⁴
$Q$ : groundwater inflow into tunnel; $K$ : constant hydraulic conductivity; $r$ : tunnel radius; $h$ : depth from the tunnel’s center line and the water head; $a_{1}$ : coefficient related to water pressure; $A :$ hydraulic conductivity gradient; : Function of Bessel; $K_{0}$ : rock cover.
$Q = 2 π K \frac{h}{\ln (\frac{2 h}{r})}$	Deep Circular tunnel. Homogeneous media. Darcy flow	Mirror method used. Inflow increase slowly with increasing of tunnel diameter	Goodman et al.⁵⁵
$Q$ : Groundwater inflow per unit length; $K$ : hydraulic conductivity; $r$ : tunnel radius; $h$ : depth from the tunnel’s center line and the water head.

Table 2 Summary of the salient analytical and semi-analytical equations proposed by different authors

Relevant empirical and semi-empirical methods

Semi-empirical and empirical methods are mostly established for specific situations where the conditions and the estimates of the considered parameters tend to reflect reality to acceptable extent. As a result, they have the features of providing more convenient results than analytical and semi-analytical methods in same situations and under same conditions. They sometimes derive from adaptation or correction of selected analytical method, or from curves interpolations. However, their effectiveness is questionable in some cases. Ordinarily, they are used at the beginning stage of projects for technical feasibility and relevant preludial design. For example, as tunnels excavation in dry conditions is always preferable for safety and economic reasons, dewatering systems are used as much as possible. But the success in these systems depends on the degree of precision of the methods employed to estimate groundwater inflows into tunnel. For quick estimates, empirical or semi-empirical methods, even analytical methods could be employed. The main equations resulting from empirical and semi-empirical methods are presented in Table 3.

Governing Equations and Parameters	Applicability	Remarks	Researchers
$Q = \frac{2 π h}{\ln (\frac{2 h}{r})} . \frac{γ}{μ} [A \frac{1}{s} . {(k)}^{α} (b + s i n θ) . (\frac{φ}{2 π} + c) . {(e_{i})}^{2}]$	Underground openings; Fractured rocks Non-Darcy flow	Consideration on Effects of hydro-mechanical coupling process.	Wang et al.²⁶
$Q$ : groundwater inflow rate ( $m^{3} / s$ ); $H$ : depth from the opening’s center line and the groundwater head; $r$ : radius of the opening; $s$ : spacing of fractures; $K$ : coefficient of lateral stress; $θ$ : angle between utmost principal stress and major permeable direction; $φ$ : angle of dilation; $e_{1}$ : initial equivalent aperture for fractures; A, b, c: associated parameters.
$Q = 0.004 + 200 π K h (\frac{1.217}{\ln (\frac{2 h}{r})} - \frac{0.741}{\ln (\frac{2 z}{r})} + \frac{0.739 r}{{(l n z)}^{2}})$	Circular tunnels, rocky media with tuff, limestone and sandstone layers. $K \in [5 \times 10^{- 8}; 2.36 \times 10^{- 6}]$ $m / s; r \in [2.3 m; 2.8 m]$ Laminar flow regime for groundwater.	Equation derived by multiple regression Analysis and stepwise algorithm.	Hadi & Homayoon²⁴
$Q$ : Groundwater inflow into tunnel ( $L / s / m$ ); $K$ : hydraulic conductivity (m/s); $r$ : Tunnel radius (m); $z$ : overburden (m); $h$ : water head (m).
$Q = 2 π K_{s i m} \frac{h}{2.3 log (2 h / r)}$ $Q = P^{n} 2 π K_{s i m} \frac{h}{2.3 log (2 h / r)}$	Circular tunnel with depth lower than 150 m; Laminar flow, Discontinuous media. The first equation is applied to rocky media with fully interconnected networks of joints. The second one for partially interconnected networks of joints.	Correction to Goodman’s equation for fractured rocks with adapted conditions. Considerations on geostructural setting.	Farhadian et al.⁵⁶
$Q$ : groundwater inflow into tunnel ( $m^{3} / s$ ); $K_{s i m}$ : empirical hydraulic conductivity( $m / s$ ); $h$ : tunnel depth from the groundwater table (m); $r$ : Radius of the tunnel (m); $n$ : number total of groups. $p$ : probability of interconnectivity.
$Q = a Q_{G}^{b}; Q = p^{n} a Q_{G}^{b}$ $a = {\begin{matrix} 3.448 F^{0.8834}; F < 0.737 \\ 3.2411 F^{0.6805}; F \geq 0.737 \end{matrix}$ $b = l n 3.463 F^{0.0342}$ $F = \frac{\sum_{i = 1}^{m} c o s α_{i}}{m} {(\frac{K_{m i n}}{K_{m a x}})}^{0, 5 φ}$	Circular tunnels with medium-depth. Anisotropic media (rock mass with discontinuities). The first equation is applied to totally interconnected-joints networks; the second for partly interconnected-joints networks.	Correction to Goodman’s equation. Considerations on geostructural setting, and on hydraulic conductivity tensor.	Gattinoni & Scesi⁵⁷
Q: actual groundwater inflow into tunnel ( $m^{3} / s$ ); $Q_{G}$ : Tunnel inflow in Goodman’s equation $m^{3} / s$ ; a, b: empirical coefficients (dimensionless); $m$ : number of sets of joints; $α_{i}$ : dip for the set of discontinuity $i$ . ; $K_{m i n}$ ; $K_{m a x}$ : minimum and maximum hydraulic tensor; $n$ : empirical coefficient; $α = - 1$ if $θ_{m i n} > 45 °$ ; $α = 1$ if ; $θ_{m i n} \leq 45 °$ : probability of interconnectivity.
$Q = 2 π K \frac{h}{\ln (\frac{2 h}{r} - 1)}$	Circular deep-seated tunnels ( $h / r \geq 3 - 4$ ); Homogeneous media, constant permeability. Darcy flow	Semi-empirical equation. There is no influence of leakage for the water table.	Karlsrud⁵⁸
$Q$ : groundwater inflow into tunnel; $h$ : piezometric head above the tunnel centre; $K$ : hydraulic conductivity; $r$ : tunnel radius.
$Q = 2 π K \frac{h}{\ln (\frac{2 h}{r})} \times \frac{1}{8}$	Circular tunnels. Homogeneous media. Darcy flow	Revision of Goodman’s equation by applying there 1/8 as reduction coefficient	Heuer⁵⁹
$Q$ : Groundwater inflow into tunnel; $h$ : piezometric head above the tunnel centre; $K$ : hydraulic conductivity; $r$ : tunnel radius.

Table 3 Summary of the salient empirical and semi-empirical equations proposed by different authors

Relevant mathematical models used in numerical methods

Mathematical models are usually employed in numerical methods when establishing conceptual models that could describe the studied situation, on the basis of geological and hydrogeological conditions. Table 4 presents some relevant of them.

Numerical model	Specificity and Applicability	Remarks	References
Discrete Fracture Network (DFN)	Real porous media. Large fractures sparsely distributed. Fractures permeability greater than that of rock mass. Simulate groundwater movements in the fractures.	Variable spatial distribution of groundwater flows in the media is considered. Complex modelling. Limited as hydraulic aperture of fractures not fully reached.	Jiang et al.⁶⁰, Li et al.⁶¹ Javadi et al.²³
Equivalent Continuous Model (ECM)	Equivalent Porous media, seepage flow through fractured rock. Darcy flow	Very limited due to the non-consideration of the real properties of the media.	Jiang et al.⁶⁰
Finite Element Method (FEM)	Modelling groundwater inflows into tunnels. Continuous media	Variable geotechnical and hydrogeological conditions	Hassani et al.⁴⁰
Boundary Element Method (BEM)	Analysis and Description of groundwater flow. Isotropic and anisotropic Porous Media. Darcy flow.	The dimensionality of the studied problem is reduced. Domain problem is changed to boundary problem.	Rasmussen and Yu⁶²
Distinct Element Method (DEM)	Simulation of stress-flow coupling. Hydromechanical properties of discontinuous rocks can be derived by equivalence.	Good representation of fractures in 3D. Direct treatment of the non-linearity behaviour of materials.	Jing⁶³

Table 4 Some relevant mathematical models used in numerical methods

Relevant numerical methods in predicting groundwater flow into tunnels

Numerical methods are currently become potential tools employed in different fields of engineering and scientific research. They are also widely used in the prediction and calculation of groundwater inflows into tunnels built in different rocky media. As already expressed, numerical methods are based on mathematical models describing the characteristics of the concerned media. According to Chiu and Chia,⁶⁴ one habitually uses numerical methods to predict groundwater inflow into tunnels when hydrological conditions are complexes. In fact, when geological and hydrogeological are complicated enough, numerical methods are often considered to approximate groundwater inflow into tunnels. Table 5 shows the relevant numerical methods employed to this purpose.

Simulation Method	Applicability and Capabilities	Remarks	Reference
FLAC 2D / FLAC 3D	Simulation of groundwater inflows or bursting in subsurface tunnels or mine in homogeneous media. Darcy’s flow regime is adopted.	Hydromechanical properties of tunnels surrounding rocks are required. FLAC can be used alone, or coupled to mechanical modelling for interactions of fluid-media.	Li et al.¹⁹; Wu et al.⁶⁵ Nikakhtar & Zare⁶⁶
MODFLOW	Prediction of groundwater inflows into shallow and deep Tunnels. Porous media. Laminar flow	Hydraulic conductivity, Hydraulic head, and others relevant hydrogeological data are needed.	Surinaidu et al.^67,68 Golian et al.⁶⁹
Conduit Flow Process (CFP) and adapted MODFLOW	Simulation of groundwater inflows into Conveyance Tunnels in heterogeneous media. Laminar and Turbulent flow.	Tunnel diameter, Reynolds Number, Permeability, Sinuosity as requirements for the CFB	Gholizadeh et al.⁷⁰
Rock Failure Process Analysis code (RFPA), 2D	Prediction of groundwater outburst in underground mine. Heterogeneous media and fractured zones. Darcy flow adopted	Geological and hydrogeological features of the areas are required for the analysis. RFPA is based on Finite Element Method (FEM).	Lianchong et al.³⁷
SEEP/W	Simulation of groundwater inflow into tunnels in saturated and unsaturated zones. Confined or unconfined aquifers. Flow regime can be Steady or Transient.	Hydraulic Conductivity and Volumetric Water Content are required.	Hassani et al.⁴⁰
Universal Distinct Element Code (UDEC), 2D	Computation of groundwater inflows rate in discontinuous media. Laminar flow	Hydraulic head, tunnel radius and joint spacing are required for optimum accuracy.	Farhadian et al.⁵⁶
COMSOL Multiphysics	Computation of groundwater inflow into tunnels and mines in both saturated and unsaturated discontinuous media. Darcy flow	Hydromechanical properties of surrounding rocks are required.	Li et al.⁷¹ Chen et al.⁷² Xu et al.⁷³

Table 5 Relevant numerical methods employed in predicting groundwater inflows into rock tunnels

Prediction based on machine learning methods

Machine Learning Methods are recently used in predicting or modelling groundwater inflows into tunnels. Table 6 summarizes the salient machine learning method used for this purpose.

Machine Learning methods	Capabilities and Applicability	Remarks	Authors
Gaussian Process Regression (GPR)	Groundwater inflows quantification into tunnels built in heterogeneous media, based on basic evaluation index and the associated criteria. Maximum Performance of inflows: $R^{2} = 0.9956$	No need to consider the relationship between hydrogeological features and water discharge rate. Large amounts of statistical data are required to obtain accurate results.	Li et al.⁷⁴
Support Vector Machine (SVM)	Prediction of Groundwater inflows into Tunnels built in karst and faults zones. Maximum Performance of inflows: $R^{2} = 0.9767$	Relevant Hydrogeological properties of the concerned media, and the depth of tunnels are required.	Li et al.⁷⁴
Convolutional Neural Network (CNN)	Prediction of groundwater inflow information in rock tunnels face.	Classification of RMR-based groundwater inflow image datasets based, and associated segmentations.	Chen et al.⁷⁵
BP Neural Network	Prediction of groundwater inrush risk in Karsts Tunnels using relevant factors	Hydrogeological factors and engineering factors could be combined for the prediction.	Yang and Ma⁷⁶
Artificial Neural Network (ANN)	Prediction of Groundwater inflows into tunnels. Maximum Performance of inflows: $R^{2} = 0.8331$	Relevant Hydrogeological properties of the media, and Tunnels depth are necessary.	Li et al.⁷⁴
Bayesian Network (BN) & GIS	Water inrush prediction in coal mine located in faults areas. The accuracy of the prediction is about 83.4%.	BN used a graphical network of probabilistic rationale. GIS is coupled to BN for water inrush quantification, and for encroachment analysis. Relevant features of openings are required.	Donglin et al.⁷⁷
Long short-term memory (LSTM)	Groundwater prediction in tunnels excavated by DB. Performance: $R^{2} = 0.9866$	Data: Tunnel depth, groundwater level, Rock Quality Designation, and Water yield property.	Mahmoodzadeh et al.⁷⁸
Deep Neural Networks (DNN)	Groundwater prediction in tunnels excavated by Drill-and-Blast. Performance: $R^{2} = 0.9815$	Data: Tunnel depth, groundwater level, Rock Quality Designation, and Water yield property.	Mahmoodzadeh et al.⁷⁸
K-nearest neighbors (KNN)	Groundwater prediction in tunnels excavated by Drill-and-Blast. Performance: $R^{2} = 0.7665$	Data: Tunnel depth, groundwater level, Rock Quality Designation, and Water yield property.	Mahmoodzadeh et al.⁷⁸
Decision Trees (DT)	Groundwater prediction in tunnels executed by DB. Performance: $R^{2} = 0.7210$	Data: Tunnel depth, groundwater level, Rock Quality Designation, and Water yield property.	Mahmoodzadeh et al.⁷⁸
Integrated model (VMD, ORELM, MOGWO)	Groundwater inflows prediction into deep mines. Prediction Performance: $R^{2} = 0.9685$	Procuration of water inflow series by VMD, Prediction of components by ORELM, Optimization by MOGWO.	Chen and Dong⁷⁹
Hybrid model (HGWO-SVR)	Prediction of water inrush into Karts Tunnels. Transport Tunnels Model Performance: $R^{2} = 0.99953$	Appropriated Rainfall data are required. HGWO algorithm optimizes SVR parameters.	Liu et al.⁸⁰

Table 6 Machine Learning methods used to predict groundwater inflows into rock tunnels

Other Methods and Approaches for forecasting groundwater inflows into rock tunnels

Due to some limitations of the above-mentioned methods in accurately predicting groundwater inflows into tunnels, other methods and approaches are designed and developed over time. Table 7 indicates the most pertinent of them.

Other methods	Applicability and Capabilities	Remarks	Investigator
Lineament Analysis	Prediction of groundwater inflows into tunnels by detecting water-bearing structures with lineaments. Crystalline bedrock, glacial zones	Method based on Satellite imagery or aerial photographs. Factors like topography, overburden type, bedrock type, and vicinity to surface water, should complete the analysis.	Mabee et al.⁸¹
Site Groundwater Rating (SGR)	Prediction of groundwater inflows into tunnels from the values ranges of the SGR factors. There is high risk for groundwater inflow into tunnels when SGR range is 700-1000 and Q > 0.28 L/sec/min. Groundwater inflow is highly probable when SGR >1000. SGR is computed as follows: SGR = $[(S_{1} + S_{2} + S_{3} + S_{4}) + S_{5}] S_{6} S_{7}$	By dividing tunnels into 6 classes, the considered parameters are aperture joints frequency (S1), schistosity (S2), crashed zones (S3), karstification (S4), Soil permeability (S5), water head above the tunnel (S6), and annual precipitation (S7).	Katibeh and Aalianvari⁸²
Random and Systematic variability of Hydraulic Conductivity	Simulation of groundwater inflows rate into tunnels. Heterogeneous media.	Considerations on the alteration trend of hydraulic conductivity with depth. Detailed characterization of the heterogeneous media is required for accurate prediction.	Jiang et al.²⁰
Geological Features Characterization	Assessment of high local groundwater inflow into rock tunnels executed by DB method. Sedimentary rocks. Inflows mainly measured in open fractures, and in fault zones.	Considerations on main geological features such as faults, dykes and open fractures, where more than 90% of groundwater inflows into tunnel can be measured.	Zarei et al.⁸³
TBM	Prediction of groundwater inflows into urban tunnels. Igneous rocks. Utmost inflows found at the contact rock-TBM and the tunnel face. Transient flow.	Identification of permeable zones by TBM. For lined tunnels, remaining seepage could be occurred. Fault zones and dikes mainly considered.	Font-Capó et al.²¹
Tunnel Inflow Classification (TIC)	Prediction of groundwater rate from the values ranges of tunnel rating. Factors describing the permeability of sedimentary rocks and the tunnel inflow are considered.	The TIC correlates tunnel class number, tunnel rating, tunnel inflow description and the tunnel inflow rate. Some correspondences are shown on the figure 6.	Zarei et al.¹²
ASTER Satellite images	Forecasting of high local groundwater inflow into tunnels. Sedimentary rocks.	Analysis of geological features detected by remote sensing surveys. Data are mainly provided by satellite imagery.	Heidari et al.⁸⁴
Blasting Vibration	Prediction of water inflow in subsea tunnels excavated by DB method. Porous media.	Comparison between initial permeability coefficient and that of under blasting vibration. Mechanical and deformations features of surrounding rocks are considered.	Liu et al.⁸⁵
Discontinuities zones and Hydrogeology, Key geological features characterization	Assessment of high groundwater inflows into rock tunnels executed by TBM. Hard rocks. Porous media. Anisotropic and heterogeneous permeability. Darcy flow.	Discontinuous zones are considered. Trends of joints sets are identified by utmost rate of water inflows. The greatest groundwater inflows match to the key lineament lines crossing the tunnels route at an angle about	Zabidi et al.¹¹
Superposition Principle	Prediction of water inflows into Subsea tunnels. Confined aquifer.	Hydrogeological data are needed. Considerations are made on seepage field, and water spurting model.	Zhang et al.⁸⁶

Table 7 Pertinent other methods and approaches for forecasting groundwater inflows into rock tunnels

Time-dependent groundwater inflow into tunnels

At great depth, groundwater inflows can be depicted by two types: temporary inflows and persistent inflows.⁸⁷ This could be understood that groundwater inflows into tunnels are time-dependent. As simulated by Liu et al.⁸⁸ below the safety thickness, groundwater inflows into tunnels evolve with time until they are stable. Owing to many complexity of the rock masses, the majority of researchers only considered the steady stage of groundwater to predict groundwater inflows into tunnels. This is one of the reasons that most of existing methods approximate groundwater inflows into tunnels. Liu et al.⁸⁸ previously studied the time-dependent groundwater inflows into tunnels and shown the associated complexity. They established an analytical method to predict groundwater inflows into tunnels constructed in anisotropic and isotropic aquifers, considering multiple factors such as conductivities, specific storage, permeability, drawdown of groundwater, etc. Logically, a prediction taking into account the time-dependent behavior of groundwater inflows seems fairer.

Discussion

Considerations on analytical, semi-analytical, empirical and semi-empirical methods

The analysed papers highlight various methods and approaches for predicting and calculating of groundwater inflows into tunnels. This paper presents thus the latest advances in methods for evaluating groundwater inflows into tunnels designed and constructed in rocky media. Most of the employed methods and approaches make assumptions which do not fully reflect the real situations of the rocky areas in which tunnels are built.⁸⁹ This allows the application of Darcy’s law and the establishment of many analytical, semi-analytical, empirical and semi-empirical equations. In reality, in heterogeneous rocky environments, Darcy’s law should not be used. As a result, accurate groundwater inflows into tunnels are not achieved. In fact, study of groundwater is uncertain in unrealistic conditions or when basing on assumptions like homogeneity and isotropy.⁹⁰ Likewise numerical methods approximate the groundwater inflows into tunnels. Indeed, as reported by Zabidi et al.¹¹ analytical, empirical and numerical methods are frequently unsuccessful in providing precise groundwater inflows into tunnels. For example, considering the same in-situ conditions, Gattinoni & Scesi⁵⁷ and Farhadian et al.⁵⁶ showed the large variation of groundwater inflows into a tunnel by comparing Goodman’s equation, Empirical formula and observations (Figure 8). It is important to point out that, empirical methods, even that they do not accurately estimate the groundwater inflows into tunnels, as shown by Farhadian et al.⁵⁶ but they are better than the analytical methods. At least, good precision level in predicting groundwater inflows into tunnels is deeply required to design efficient dewatering systems.

Figure 8 A comparison between Goodman’s equation, empirical formula and observation for groundwater inflow in Begamo tunnel.⁵⁷

Considerations on numerical methods

Regarding the numerical methods, they could improve the accurate prediction and calculation of groundwater inflows into rock tunnels. However, all the relevant characteristics of the rocky media are not always fully appreciated. In fact, the necessary data for the full use of these methods are usually numerous. In addition to the mentioned difficulties, we must also consider the time consuming and cost factors.⁹¹ The need to quickly estimate an accurate groundwater inflows into tunnels is extremely important. We also emphasize that numerical methods are usually associated with mathematical models. The latter generally describe rocky environments with simplifying assumptions. Indeed, the exact conditions and properties of said environments are difficult to model. Thereby, as reported by Park et al.⁹² the discretization provided by numerical methods is habitually rude, then they also exaggerate groundwater inflows into tunnels. Hence, numerical methods are limited to simplified conceptual models including limited data. Consequently, they could not also accurately estimate groundwater inflows in tunnels, and thus, as Sedghi and Zhan⁹³ reported, they are not always the optimal choice.

Considerations on machines learning methods

In order to improve the accuracy of predicting groundwater inflows into tunnels, many efforts are already made. Many approaches and techniques are considered as shown through this paper. Nowadays, Machine Learning methods are also employed to forecast groundwater inflows into tunnels. Nonetheless, as demonstrated by Mahmoodzadeh et al.⁷⁸ a good precision of these methods impose huge amounts of relevant data. For this purpose, likewise that numerical methods, costs factors and time-consuming may be regarded as some obstacles in getting precise prediction. Indeed, we should verify how hybrid ML techniques can improve the prediction precision of groundwater inflows into tunnels. For instance, Liu et al.⁸⁰ used a hybrid model to predict groundwater inrush into karts tunnels and found good results. It would therefore be interesting to investigate in-depth the application of these methods in different geological and hydrogeological conditions.

Considerations on other methods or approaches

As presented in this paper, other methods or approaches are also implemented in order to predict groundwater inflows into rock tunnels. Most of them take advantage of the geological characterization of rocks. They identify the geological features most likely to store groundwater and facilitate flow-paths. These methods also require a lot of relevant data and subsurface exploration for high accuracy level. Further studies based on these methods for the accurate assessment of groundwater inflows into tunnels are needed.

Considerations on time-dependency of groundwater inflows

The time-dependency of groundwater inflows is another interesting factor to consider in the search for an accurate estimation of groundwater inflows into tunnels. As studied by Liu et al.⁹⁴ most of the methods do not take into account this property. This is probably another reason why most of the existing methods overestimate the groundwater inflow into tunnels. Realistic evaluation of groundwater inflows into tunnels could depend on many potential factors including the time-dependent behavior of groundwater inflows into tunnels. It could also help in designing reliable dewatering system facilitating better accessibility and tunnelling operations.⁹² In fact, as reported by Xia et al.⁹⁵ the time-dependent trend of groundwater inflow into tunnel depends on the variation of hydraulic conductivity and the water drawdown. For an illustration, Figure 9 shows the time-dependency of groundwater inflow into tunnels with the variation of water head drawdown, according to Liu et al.⁸⁸

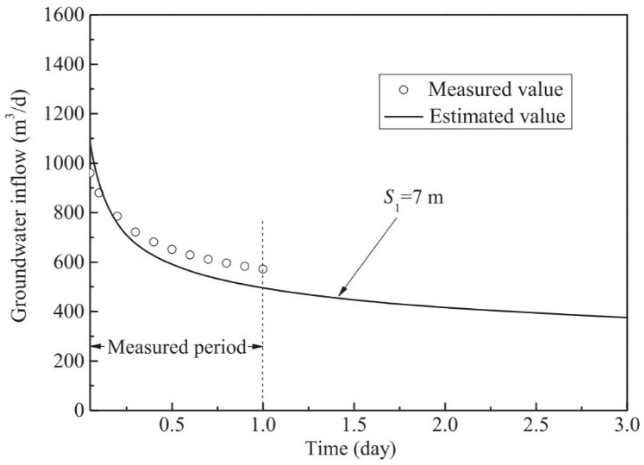
Figure 9 An illustration of the time-dependency of groundwater inflows into tunnels for a drawdown represented by S₁ = 7 m, according to Liu et al.⁸⁸

Considerations on relevant parameters

As already mentioned, many potential factors influence the prediction of groundwater inflows into tunnels. Among these factors related to the surrounding rocks or the aquifer, we can quote, according to Bahrami et al.⁹¹ hydraulic head, transmissivity, hydraulic conductivity, aquifer thickness, specific storage, porosity, rainfall data, etc. In almost all of the mentioned methods, not all of these factors were fully taken into account. Concerning the hydraulic conductivity, many equations consider it constant. But in reality, tunnels are built in anisotropic medium. Taking into account the variation of such a parameter can improve the precision in the assessment of groundwater inflows into rock tunnels. Regarding the hydraulic head which is usually assumed as constant, but in real situation, groundwater inflows affect it progressively. Then, there is thus drawdown. It is only a few analytical equations that consider the effect of the groundwater table drawdown. The variation of the others factors also influence the groundwater inflows into tunnels. For instance, the variation of rock mass permeability has great effects on groundwater inflows into tunnels. As Perello et al.⁹⁶ said in the case of crystalline rocks and in mountain areas, the distribution of rock masses permeability is discontinuous and inhomogeneous. In addition, especially in discontinuous media, geo-structural setting of rock mass influence greatly the groundwater inflow into tunnels, but is almost rarely integrate in the analytical equations.⁵⁷

Considerations on groundwater flow regime

Another potential factor of interest is the groundwater flow regime in tunnels. In the most of the presented methods and equations, emphasis are put forward on Darcy flow regime. Few of the existing methods and equations take into account the transient flow and the non-Darcian flow. The analysis of groundwater inflow into tunnels reveals that flow regime is initially transient, then it becomes stable Liu et al.³⁸ This is also another reason why many existing equations or methods do not fully estimate the groundwater inflows into tunnels by considering only the stationary flow phase. In fault and karts zones particularly, as reported by Shi et al.^97,98 the flow velocity is high, and Darcy flow cannot be considered. Deep tunnels generally cross faults areas where the groundwater flow regime is non-Darcian. As experimented by Shi et al.⁹⁸ in these zones, water inrush can occur owing to the high permeability and weak strength of rocks. Regarding the turbulent flow, there is almost no consideration about it. However, in the cases of very high groundwater inflows (inrush) and extremely high groundwater inflows (water burst), the flow regime may be turbulent. Therefore, the realistic flow of groundwater should be fully considered for a best prediction of groundwater inflows into rock tunnels.

Considerations on long-term stability of tunnels

Note that stress field perturbations created by the excavations, generate instability to tunnels. This instability is boosted by the influx of groundwater into tunnels.⁹⁹ Indeed, as illustrated in the Figure 3, EDZ and EdZ, which are generated by stress redistribution, clearly influence the permeability of surrounding rocks of tunnels. When such a consideration is ignored, the stability and longevity of tunnels are decreased, as the calculated groundwater inflows are lower than the real value.¹⁰⁰ Although precise prediction and calculation of groundwater inflows into tunnels or into underground structures remains a challenge, but it is a vital need. Indeed, the long-term stability of tunnels depends on it. Lack of precision on groundwater inflows can cause groundwater leaks in tunnels by designing unsuitable treatment and support systems. Then groundwater leaks provoke severe damages such as: alteration and deformation of tunnels structures, ageing tunnels components, unfavorable environmental effects, and embarrassment of users.¹⁰¹ Accordingly, it affect thus the long-term stability of tunnels, as water greatly influences the time-dependent behavior (creep) of surrounding rocks.¹⁰² Figure 10 shows how the lack of precision for groundwater inflows can affect the long-term stability of tunnels.

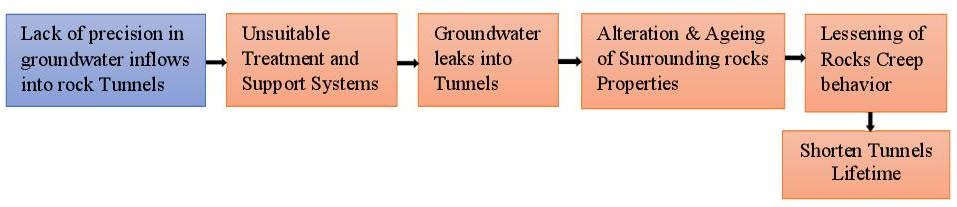
Figure 10 Effects of precision’s lack for groundwater inflows on long-term stability of tunnels.

Conclusion, recommendation and future
trends

Conclusion

This paper outlines and discusses methods for assessing groundwater inflows into rock tunnels. It constitutes thus a synthesis of the latest progresses in the field concerning the prediction of groundwater inflows into tunnels. Precise predictions or evaluations of groundwater inflows into tunnels are still unsolved problems in hydrogeology and all allied sciences. Nevertheless, this review shows that scholars and researchers developed many methods and almost all techniques to solve this significant issue. This may therefore inspire them to apply or develop newest techniques or ideas in this exciting topic. Thus, the prediction of groundwater inflows in rock tunnels will be further enriched, while further improving their accuracy. Nonetheless, some other conclusions are summarized as follows:

Analytical, semi-analytical, empirical or semi-empirical methods must be adapted as close as possible according to the realistic conditions of the rocks media traversed by tunnels.
Numerical methods cannot fully replace the aforementioned methods. They can be used for comparison purposes by seeking to improve as much as possible the accuracy of the calculation for groundwater inflows into tunnels.
Other methods employed to predict groundwater inflows into rock tunnels require huge relevant data and engineering judgements in order to improve the accuracy of the prediction.
A better prediction of groundwater inflows into rock tunnels must take into account the time-dependent behavior of groundwater inflows with the associated salient characteristics of the concerned media.

Recommendations and future trends

Research on groundwater inflows into rock tunnels would be much more beneficial scientifically, technically and economically, and fructuous precisions could be achieved through the following recommendations:

Increase the advantage of more reliable particular models and reduce their limitations. Close monitoring of relevant data is mandatory for accurate experimental results.
Determine the influence of all relevant parameters for different methods employed and obtain efficient and strong models but easy to use for groundwater inflows prediction.
Develop databases as much as possible by accumulating accurate and adequate historical data for different cases of groundwater inflows into rock tunnels.
Investigate more on machines learning techniques, and strong and efficient App may be established for data collection and for fast computations.

Despite numerous studies already conducted, there are still several areas of research which deserve further studies in order to support accurate predictions of groundwater inflows into rock tunnels. Although it remains as challenging tasks, but it is of tremendous importance that the future trends may focus on the following points:

Multi-parameters analysis for precise evaluations of groundwater inflows into rock tunnels based on Analytical, Empirical and Numerical methods.
The exact assessment of groundwater inflows into tunnels based on the time-dependency of groundwater and on rock masses geo-structural setting.
Prediction of groundwater inflows into deep rock tunnels based on realistic flow regime and Machines Learning Techniques.