International Journal of
eISSN: 2576-4454


Research Article Volume 1 Issue 1
1Department of Civil and Environmental Engineering and Water Resources Research Center, University of Hawaii at Manoa, USA
2Department of Water Engineering, University of Tabriz, Iran
3Department of Soil Science, University of Tehran, Iran
Correspondence: Sayed M Bateni, Department of Civil and Environmental Engineering and Water Resources Research Center, University of Hawaii at Manoa, Hawaii, USA, Tel 808-956-4249, Fax 808-956-5014
Received: May 19, 2017 | Published: July 27, 2017
Citation: Lum M, Bateni SM, Shiri J, et al. Estimation of reference evapotranspiration from climatic data. Int J Hydro. 2017;1(1):25-30. DOI: 10.15406/ijh.2017.01.00005
This study investigated the capability of M5 Model Tree (M5MT) to predict reference evapotranspiration (ET0). M5MT was trained and tested with climatic data from eight weather stations located in coastal areas of Iran for the years 2000-2008. It was validated with climatic data from seven California Irrigation Management Information System (CIMIS) weather stations for the year 2015. Four different data combinations were utilized to train, test, and validate the M5MT model. These were: daily mean air temperature, wind speed, relative humidity, and solar radiation (configuration 1); daily mean air temperature and solar radiation (configuration 2); daily mean air temperature and relative humidity (configuration 3); and daily maximum, minimum, and mean air temperature, and extraterrestrial radiation (configuration 4). The Penman-Monteith (PM) equation was used as a standard method to provide target ET0 values. Mean absolute error (MAE), root mean square error (RMSE), and the coefficient of determination (R2) were used to evaluate the performance of the M5MT models developed with different input configurations. Results indicated that M5MT was able to successfully estimate ET0. Configuration 1 provided the most accurate results. Configuration 2 showed to have the variables that have a greater influence on ET0 than configuration 3. Configuration 4 performed the worst. MAE of ET0 estimates from M5MT1 was respectively 29%, 55%, and 91% lower than that of M5MT2, M5MT3, and M5MT4, when the model is validated in California. Also, RMSE from M5MT1 was 29%, 59%, and 125% smaller than that of M5MT2, M5MT3, and M5MT4, respectively.
Evapotranspiration (ET) is an important component of the hydrologic cycle, which significantly influences crop water requirement and water resource management.1 Accurate ET estimates enable the proper determination of water budgeting and allocation, and thus improves water use efficiency of irrigation systems. In situ methods are often used to measure ET in a controlled crop area, but they are costly, labor intensive, and only provide localized estimates .2,3 To avoid the high costs, empirical, artificial intelligence, and physical models have been developed to estimate reference ET (ET0).4 ET0 is the combined process of evaporation and transpiration from a theoretical grass surface with an assumed height of 0.12meter, a surface resistance of 70 s/m, and a surface albedo of 0.23.5 The Penman-Monteith (PM) equation has been accepted as a standard approach to estimate ET0. However, this method requires many climatic variables that are typically unavailable.6 Due to the drawbacks of in situ methods and the PM equation, Artificial Intelligence (AI)-based approaches have been used to estimate ET07 utilized Artificial Neural Network (ANN) to approximate ET0 in the arid, semi-arid, and sub-humid regions of Inner Mongolia. In comparison with Multiple Linear Regressions (MLRs), ANN showed more accurate estimates.4 estimated daily ET0 in Northern Spain using Gene Expression Programming (GEP) and compared its performance with those of the Adaptive Neuro-Fuzzy Inference System (ANFIS), Hargreaves-Semani, and Priestley-Taylor models. Results indicated that GEP provided the most accurate estimates followed by ANFIS 8 used ANN to predict ET0 in arid and semi-arid areas of northwest China. ANN was found to estimate ET0 more accurately than MLRs, Priestley-Taylor, Hargreaves-Semani, and Penman-Monteith (PM) equations 9 predicted ET0 in northern, mid, and southern part of Iraq using Extreme Learning Machines (ELM). Compared to the PM equation and Feed Forward Back Propagation (FFBP) models, ELM estimated ET0 better Recently, M5 Model Tree (M5MT) has been used in many engineering problems, and showed promising results.10−12 M5MT is an extension of a regression tree and provides the user with multiple linear functions.1‒13 This approach is capable of handling high dimensional datasets and the resulting model tree is significantly smaller and more precise than regression trees.14 Moreover, the M5MT is not a black-box and provides a relationship between the independent and dependent variables.11 Several studies have shown M5MT to be an effective technique to provide accurate results15showed M5MT is advantageous over ANN because it generated more accurate wave height estimates11found that the performance of M5MT was comparable to ANN, but indicated that the training process of M5MT was faster than that of ANN14 performed a comparison of M5MT and Support Vector Machines (SVM) in forecasting daily river flow. Results showed M5MT performed similar to SVM, but it is computationally less expensive16concluded M5MT to be better than ANN as it provided a more straightforward structure consisting of linear regression equations. The objective of this study is to estimate ET0 from climatic data using M5MT. Four different combinations of climatic data were used in M5MT. These combinations were daily mean air temperature, wind speed, relative humidity, and solar radiation (configuration 1); daily mean air temperature and solar radiation (configuration 2); daily mean air temperature and relative humidity (configuration 3); and daily maximum, minimum, and mean air temperature, and extraterrestrial radiation (configuration 4). An assessment of which data combination has the most amount of information about ET0 was made.
Studied sites and data: Daily climatic data as well as ET0 estimates from the PM equation were used to train, test, and validate the M5MT model. The training dataset consisted of data from eight coastal weather stations in Iran, collected from 2000 to 2007. The testing dataset contained data from the same eight stations, but for 2008. Performance of the M5MT models was validated with seven California Irrigation Management Information System (CIMIS) weather stations in 2015. CIMIS dataset was used for models validation to evaluate their feasibility in other regions, and examine whether they are applicable in areas that they were not trained in. Figure 1 & Figure 2 show the spatial distribution of the utilized weather stations in Iran and California, respectively. The recorded data consisted of daily average relative humidity (RHmean), and wind speed (Ws), daily maximum, minimum and mean air temperature (Tmax, Tmin, and Tmean), and incoming solar radiation (Rs). Table 1 lists the geographical coordinates of each weather station and the corresponding annual averages of the collected data. ET0 is the reference evapotranspiration (mm/d), Δ is the slope of saturation vapor pressure function (kPa/°C), Rn is the net radiation (MJ/m2day), Ra is extraterrestrial radiation (mm/d), G is the soil heat flux density (MJ/m2day), γ is the psychrometric constant (kPa/°C), Tmean is the mean air temperature (°C), Tmax is the daily maximum air temperature (°C), Tmin is the daily minimum air temperature (°C), Ws is the daily mean wind speed at a height of 2 m (m/s), RH is relative humidity (%), es is the saturation vapor pressure (kPa), and ea is the actual vapor pressure (kPa). The commonly used equations for the estimation of ET0 are presented in Table 2. Based on the proposed equations in Table 2 and the study conducted by,4 four input combinations were used to predict ET0. The following data configurations were used to train, test, and validate M5MT:
Configuration 1: Ws, RHmean, Tmean, and Rs [M5MT1]
Configuration 2: Tmean and Rs [M5MT2]
Configuration 3: Tmean and RHmean [M5MT3]
Configuration 4: Tmean, Tmax, Tmin and Ra [M5MT4]
Three statistical metrics (mean absolute error (MAE), root mean square error (RMSE), and the coefficient of determination (R2) were used to compare performance of the four M5MT models (i.e., M5MT1, M5MT2, M5MT3, and M5MT4). These statistical metrics are given below:
;(1)
;(2)
;(3)
Country |
Station |
Location |
|
Climatic Parameters |
|
|
|
|
||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
altitude (m) |
Latitude (°) |
Longitude (°) |
Tmax (°C) |
Tmin (°C) |
Tmean (°C) |
Rs (MJ/m2d) |
Ws (m/s) |
Rhmean (%) |
Iran |
Abadan |
6.6 |
30.2 |
48.2 |
34 |
18.9 |
26.3 |
19.4 |
3.2 |
64.7 |
Ahwaz |
22.5 |
31.2 |
48.4 |
34 |
19.4 |
26.6 |
18.5 |
2.4 |
65.6 |
|
Bandar-e-Abbas |
9.8 |
27.1 |
56.2 |
32 |
23.4 |
27.5 |
17.4 |
3.7 |
78.6 |
|
Bandar-e-Lenge |
22.7 |
26.3 |
54.2 |
33 |
21.9 |
27.2 |
19.4 |
3.7 |
73.2 |
|
Bushehr |
9 |
28.6 |
50.5 |
30 |
20.6 |
25.3 |
18.3 |
3.5 |
75.8 |
|
Gorgan |
13.3 |
36.5 |
54.1 |
23 |
12.9 |
18.2 |
15.8 |
2.6 |
63.6 |
|
Rasht |
-8.6 |
37.1 |
49.4 |
21 |
12.3 |
16.6 |
15.8 |
1.6 |
76.5 |
|
Sari |
23 |
36.3 |
53 |
23 |
13.5 |
18 |
16.3 |
2.2 |
75.6 |
|
California, USA |
Atascadero |
269.8 |
35.5 |
-121 |
24 |
5.8 |
14.1 |
16.5 |
1.2 |
64.2 |
Delano |
91.4 |
35.8 |
-119 |
27 |
9.8 |
17.6 |
18.6 |
1.4 |
55.6 |
|
Gilroy |
56.4 |
37 |
-122 |
24 |
7.5 |
14.8 |
17.4 |
2.2 |
67.2 |
|
Arleta |
298.7 |
34.3 |
-118 |
26 |
11.6 |
18.3 |
18.6 |
1.6 |
49.7 |
|
Gerber South |
75 |
40 |
-122 |
25 |
9.9 |
17.2 |
18.3 |
2.3 |
59.8 |
|
Woodland |
25 |
38.7 |
-122 |
25 |
9.8 |
17.1 |
17.5 |
2.2 |
54.8 |
|
|
Diamond Springs |
624.8 |
38.6 |
-121 |
22 |
10.5 |
16.1 |
17.7 |
1.7 |
49.9 |
Table 1 Geographical location of stations and annual averages of climatic data
Study |
ET0 Equation |
Penman-Monteith et al. [2] |
|
Makkink [20] |
|
Romanenko [21] |
|
Hargreaves & Samani [22] |
|
Table 2 Different ET0 equations
Where n is the number of data points, Oi and Pi are the ith estimated ET0 values respectively from the PM and M5MT models, and O ̅ and P ̅ are the mean predicted ET0 values from the respective models. The R2 signifies the percentage of data that conforms to the regression line at a 45-degree angle. If all points coincide with the regression line, the variation between the variables can be explained by a linear relationship and R2 would result in an optimal value of one. MAE describes the average of a set of absolute errors with an optimal value of zero. Since only the magnitude of the error is considered, non-negative values are obtained with no upper bound. RMSE is a measure of difference between the observed and simulated values. The greater concentration of data around the 1:1 line, the lower the value of RMSE becomes. RMSE does not have an upper bound and its optimal value is zero.
M5 Model Tree (M5MT): M5MT is an improvement of a regression tree, which replaces specific numerical values with linear regression functions relating input variables to corresponding output variables.12,13 Two different stages are involved to generate a final model tree. The first stage divides the input space into different regions that correspond to nodes within a tree-like structure. The standard deviation of each region is calculated and corresponds to the amount of error for each of the nodes created. Next, the expected error reduction is calculated for every value propagating to a specific node. The calculated error uses the following formula known as the standard deviation reduction (SDR):1
Where T is the set of values that reach a node, Ti is the subset of values that have the ith outcome of a potential set, A is the final amount of values in set T, and sd is the standard deviation. This dividing process results in the algorithm to perform iterations, which generates subsequent nodes that will exhibit a reduction in standard deviation from the previous nodes. The algorithm will continue to iterate, considering all possible splits, and ends when the least expected error is attained.17The conclusion of the first stage leaves the model tree to have large structure, which initiates pruning of the overgrown model tree (i.e., the second stage of M5MT).12 Pruning will occur if the estimated error of nodes branched below a specific node is greater.1−18 Linear regression equations will replace the pruned nodes, resulting in a more simplified and accurate model tree. 15‒19
Building M5 Model Tree: This study used WEKA (Waikato Environment for Knowledge Analysis), which is a data mining software to estimate ET0. It consists of a wide variety of machine learning algorithms including M5MT. The WEKA interface provided different testing options (i.e., percentage split, train-test, and cross validation) to assist in the modeling process. Among the three aforementioned options, the Train-Test method was selected because of its better performance (Table 3).
Methods |
MAE (mm/d) |
RMSE (mm/d) |
R2 |
Percentage Split |
0.255 |
0.3422 |
0.9904 |
Train-Test |
0.2328 |
0.3189 |
0.9914 |
Cross Validation |
0.2396 |
0.3337 |
0.9906 |
Table 3 Performance of M5MT for different testing options
Performance of M5MT models in Iran (training and testing stages): Table 4 shows MAE, RMSE, and R2 of ET0 estimates from the four M5MT models for training and testing stages. The training process resulted in MAE, RMSE, and R2 values ranging between 0.33−0.76mm/d,0.47‒1.03mm/d, and 0.81−0.96, respectively. The testing stage showed similar values that ranged between 0.38‒0.77mm/d (MAE), 0.55−1.06mm/d (RMSE), and 0.80-0.95 (R2). It was observed that the presence or absence of certain input parameters influenced the performance of the models. Comparing the models with two input variables, M5MT3 (whose inputs were Tmean and RHmean) had higher MAE (0.76mm/d) and RMSE (1.0mm/d) than M5MT2 (whose inputs were Tmean and Rs) in the training stage. Solar radiation tends to have a greater effect on ET0, as replacing mean relative humidity by solar radiation increased accuracy in the training phase and decreased MAE and RMSE by 23% and 21%, respectively. This is in agreement with the results from the testing stage, in which a respective 20% and 15% decrease in MAE and RMSE was observed when solar radiation was used in lieu of mean relative humidity. Assessing the performance of the M5MT models with four input variables during the training stage, M5MT4 (whose inputs were Tmean, Tmax, Tmin and Ra) had larger MAE (0.53mm/d), RMSE (0.73mm/d) , lower R2 (0.91) values than M5MT1 (whose inputs were W2, RHmean, Tmean, and Rs). This is consistent with the testing phase because MAE and RMSE are decreased by 47% and 49% by using M5MT1 instead of M5MT4. Figure 3A & Figure 3B show estimated ET0 values from the four M5MT models versus PM ET0 estimates for training and testing stages, respectively. The concentration of data around the 1:1 line in Figure 3A & Figure 3B reflects the low RMSE values obtained in both training and testing stages. In general, the small MAE and RMSE and high R2 suggest that M5MT can accurately estimate ET0. Overall, the results in Figure 3A & Figure 3B and Table 4 indicate that the combination M5MT1 provided the most accurate ET0 estimates during the training and testing stages. In the training stage, MAE (RMSE) of ET0 estimates from M5MT1 were respectively 88% (81%), 130% (119%) and 61% (55%) lower than those of M5MT2, M5MT3 and M5MT4. A similar tendency was seen in the testing stage with MAE (RMSE) values of M5MT1 were 68% (67%), 103% (93%), and 47% (49%) lower than those of M5MT2, M5MT3 and M5MT4, respectively.
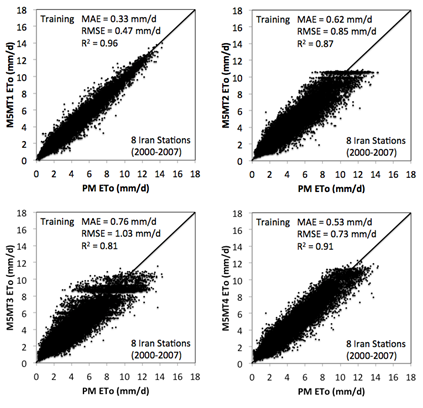
|
Training: Iran (2000-2007) |
|
Testing: Iran (2008) |
|
|
|||
|---|---|---|---|---|---|---|---|---|
|
M5MT1 |
M5MT2 |
M5MT3 |
M5MT4 |
M5MT1 |
M5MT2 |
M5MT3 |
M5MT4 |
MAE (mm/d) |
0.33 |
0.62 |
0.76 |
0.53 |
0.38 |
0.64 |
0.77 |
0.56 |
RMSE (mm/d) |
0.47 |
0.85 |
1.03 |
0.73 |
0.55 |
0.92 |
1.06 |
0.82 |
R2 |
0.96 |
0.87 |
0.81 |
0.91 |
0.95 |
0.85 |
0.8 |
0.88 |
Table 4 Statistical metrics of M5MT models for training and testing stages
Performance of M5MT models in California (validation stage): To validate the robustness of the M5MT models, they were applied to seven CIMIS weather stations in California. It should be noted that the CIMIS data was not used to train the M5MT models. The statistical metrics of the M5MT models were given in Table 5. MAE, RMSE, and R2 values ranged between 0.65-1.24mm/d, 0.80-1.80mm/d, and 0.68-0.90, respectively Table 5. Figure 4 illustrates plots of ET0 estimates from the four M5MT models versus PM ET0 estimates at the seven CIMIS stations. Performance of the models can be ranked as follows: M5MT1, M5MT2, M5MT3, and M5MT4. Similar to the training and testing phases, M5MT1 outperformed the other models when tested at the California stations. Although no CIMIS data was used to train the M5MT1 model, it performed well when applied to the stations in California. This implies that the M5MT1 can provide accurate results in other regions. Figure 4 & Figure 5 showed that the M5MT1 model with MAE, RMSE, and R2 values of 0.65mm/d, 0.80mm/d, and 0.90, respectively, can be selected as the best M5MT model for ET0 estimation. With only two input parameters (i.e., M5MT2 and M5MT3), M5MT2 showed to provide better results than M5MT3. This implies that a combination of Rs and Tmean contributes more significantly towards the estimation of ET0 than a combination of RHmean and Tmean. Figure 5 indicates time series of ET0 estimates from M5MT1 and PM models at four CIMIS stations (i.e., Delano, Gerber South, Woodland, and Diamond Springs). As shown, the estimated ET0 values from M5MT1 agree well with those of the PM equation. Remarkably, ET0 estimates from M5MT1 captured the fluctuations of the PM ET0 values. Compared to M5MT1, MAE values of M5MT2, M5MT3, and M5MT4 were respectively 29%, 55%, and 91% larger. Also, RMSE values from M5MT2, M5MT3, and M5MT4 were respectively 29%, 59%, and 125% greater than that of M5MT1.
|
Validation: california (2015) |
|
||
|---|---|---|---|---|
|
M5MT1 |
M5MT2 |
M5MT3 |
M5MT4 |
MAE (mm/d) |
0.65 |
0.84 |
1.01 |
1.24 |
RMSE (mm/d) |
0.8 |
1.03 |
1.27 |
1.8 |
R2 |
0.9 |
0.93 |
0.74 |
0.68 |
Table 5 Statistical metrics of M5MT models for validation stage
This study examined the ability of M5 Model Tree (M5MT) to estimate reference evapotranspiration (ET0) from climatic data. Four combinations of data were used in the M5MT model. These combinations were daily mean air temperature, wind speed, relative humidity, and solar radiation (configuration 1); daily mean air temperature and solar radiation (configuration 2); daily mean air temperature and relative humidity (configuration 3); and daily maximum, minimum, and mean air temperature, and extraterrestrial radiation (configuration 4). The objective was to determine which data combination had the most significant amount of information on ET0. The results indicated that M5MT can estimate ET0 accurately. Data combination 1 generated the most accurate ET0 estimates and thus consisted of variables that have the most amount of information on ET0 compared to data combinations 2, 3, and 4. Comparing M5MT models with two input variables, configuration 2 resulted in more accurate ET0 estimates than configuration 3. This suggests the greater importance of solar radiation and air temperature in comparison to relative humidity and air temperature to estimate ET0.
None
None.

©2017 Lum, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.