Within the framework of the theory of plane steady filtration of an incompressible fluid according to Darcy’s law, two limiting schemes modeling the filtration flows under the Joukowski tongue through a soil massif spread over an impermeable foundation or strongly permeable confined water-bearing horizon are considered.

The problem on the flow around a tongue was investigated for the first time by Joukowski NE in,¹ where the modified Kirchhoff method from the theory of jets was used for solving problems with a free surface, and a special analytical function, which is widely applied in the theory of filtration, was introduced. After this publication, the function and the problem, as well as the tongue, were named after Joukowski.² This study opened the possibility of the mathematical modeling of motions under the Joukowski tongue and initiated investigations of the specified class of filtration flows (see, for example, reviews).^2,3 At the same time, there are no studies devoted to special investigation of the effect of evaporation or infiltration on the pattern of motions. These important physical factors have been disregarded in exact analytical solutions of similar problems until now. In this work, we studied the effect of evaporation or infiltration by the example of two schemes that arise in the flow around the Joukowski tongue. The first scheme corresponds to the case in which the soil layer is underlain to the entire extent by an impermeable basis, and evaporation takes place from the free surface. In the second scheme, the underlying layer represents an entirely well permeable confined water- bearing horizon and there is infiltration on the free surface. We present a uniform technique of solving the problems, which enables us to take into account also other basic filtration characteristics in the investigation (the backwater both from the side of the underlying impermeable basis and the highly permeable confined water bearing horizon and the soil capillarity) and to estimate the joint effect of these factors on the pattern of the phenomenon. Evaporation or infiltration on the free surface are studied using the Polubarinova Kochina method^2,3 and the ways of conformal mapping⁴⁻⁶ developed for regions of a special type:⁴ in this case, the mixed multiparameter boundary-value problems of the theory of analytical functions are solved. Taking into account the typical features of the flows under consideration makes it possible to present the solutions through elementary functions, which makes their use most simple and convenient. The results of numerical calculations are presented, and the hydrodynamic analysis of the effect of evaporation or infiltration, as well as all physical parameters of schemes on the filtration characteristics, is given.

We consider the 2D (in the vertical plane) steady filtration of a fluid in a homogeneous and isotropic soil layer of thickness T, underlain by a horizontal impermeable foundation (confining bed) under uniform evaporation of intensity ε (0 <ε <1) from the free surface (Figure 1). The flow is provided by the water inflow from the left-hand side of the flooding band AB with the time-invariable fluid layer. The impermeable vertical screen in the form of the Joukowski tongue AF of S in length, the basis of which is located inside the layer (Figure 1), serves as the right-hand edge of the flooding band. We introduce the complex motion potential $\omega =\varphi +i\psi {\sin }^{-1}\theta$(ϕ is the velocity potential, and ψ is the stream function) and the complex coordinate$z=x+iy$referred correspondingly to κTand T, where κ=const is the soil-filtration coefficient. The problem consists in finding the complex potential ω(z) as the function, which is analytical in the filtration region z and satisfies the following boundary conditions:

$\text{AB: y = 0, }\phi \text{ = -H;}$

$\text{BC: y = -T, }\psi \text{ = 0;}$

$\text{CDE: }\phi {\text{ = -Y+h}}_{\text{C}}\text{, }\psi \text{ = -}\epsilon x+Q\text{;}$(1)

$EA:x=0,\psi =Q,$
Where h is the static height of capillary rise of soil waters and Qis the desired filtration flow rate of the water. Assuming that CDE x = L in the second condition in Eq. (1) for the portion CDE, we obtain

$Q=\epsilon L$  (2)

The problem is solved by using the Polubarinova Kochina method,^2,3 which is based on the analytical theory of the linear differential equations of the Fuks class.⁷ We introduce an auxiliary canonical variable $\zeta$ and the functions z($\zeta$), which conformally maps the upper half-plane Im $\zeta$ > 0 to the flow region z at the correspondence of points ${\zeta }_B=0,{\zeta }_C=1,{\zeta }_E=\infty$, and also the functions -$\frac{d\omega }{d\xi }$and -$\frac{dz}{d\xi }$. Determining the characteristic parameters of the last functions near the regular special points,_2,7 we find that they are the linear combinations of two branches of the following Riemann function:2

$P\left\{\begin{array}{cc}\begin{array}{ccccc}-{\zeta }_A& 0& 1& {\zeta }_D& \infty \\ -1/2& -1& -(1+V)/2& 0& 3/2\\ -1/2& -1/2& -(1-V)/2& 2& 2\end{array}& \zeta \end{array}\right\}=\frac{\text{Y}}{\zeta \sqrt{\left(\zeta +{\zeta }_A\right){\left(1-\zeta \right)}^{\left(1+v\right)}}}$

$Y= P\left\{\begin{array}{cc}\begin{array}{cccc}0& 1& {\zeta }_D& \infty \\ 0& 0& 0& -(1+v)/2\\ 1/2& v& 2& -v/2\end{array}& \zeta \end{array}\right\}$ (3)

Where$\pi \nu =2arc\cot \sqrt{\epsilon }$, it can be seen that the point $\zeta =-{\zeta }_A$ is the ordinary point for the function Y representing the last Riemann symbol. The following linear differential equation of the Fuks class with four regular special points corresponds to this symbol:

$\text{Y ''}+\left(\frac{1}{2\zeta }+\frac{1-v}{\zeta -1}-\frac{1}{\zeta -{\zeta }_D}\right)\text{Y '}+\frac{v(1+v)\zeta +{\lambda }_0}{4\zeta (\zeta -1)(\zeta -{\zeta }_D)}\text{Y = 0}$(4)

Where λ0 is the accessory parameter, we recall that the prototype ${\zeta }_D$of the cut vertex Din Eq. (4) and also the accessory constant λ0 remain unknown in the formulation of the problem. We consider the region of the complex velocity w (Figure 2) corresponding to boundary conditions (1). This region, which is represented by a circular quadrangle with two right angles, the angle of πν at the vertex C, and a cut with the vertex at the point D, belongs to the class of polygons in polar grids.⁴⁻⁶  Similar regions are quite characteristic for many problems of underground hydromechanics: in filtration from a mole sprinkler,⁸ in the flows of fresh waters in lenses formed above salty waters at rest during filtration from reservoirs and channels,⁹ and in the flow around the Joukowski tongue in the presence of salty up thrust waters¹⁰ (see also).^2,3 The replacement of variables $\zeta ={\tanh }^{2}t$transfers the upper half-plane $\zeta$ into the horizontal semiband Ret > 0, 0 < Imt < 0.5π of the plane t, and the integrals Yof Eq. (4), which are constructed by the technique developed previously in,⁴⁻⁶  are transformed to the form

${\text{Y}}_{\text{1}}=\frac{\text{cosh }t\text{ cosh }vt+\text{Csinh }t\text{ sinh }vt}{{\text{cosh}}^{\text{1+}v}t}$  ${\text{Y}}_{{}_2}=\frac{\text{cosh }t\text{ sinh }vt+\text{Csinh }t\text{ cosh }vt}{{\text{cosh}}^{\text{1+}v}t}$ (5)

Considering relations (3) and (5) and taking into account that $w=\frac{d\omega }{dz}$ , we come to the dependences

$\frac{d\omega }{dt}=\sqrt{\omega }M\frac{\cosh t\sinh vt+C\sinh t\cosh vt}{\Delta (t)}$

$\frac{dz}{dt}=M\frac{\cosh t\cosh vt+C\sinh tsinhvt}{\Delta (t)}$

$\Delta (t)=\sqrt{{\sin }^{2}a+{\sinh }^{2}t}$ (6)

Where М > 0 is the scale constant of modeling, The writing of representations (6) for different portions of the boundary of the region t with subsequent integration over the entire contour of the auxiliary region of the parametrical variable t results in the expressions for set S, T, and H and the desired values of d and L; the flow rate in this case is calculated from formula (2). In Figure 1, we show the flow pattern calculated at ε =0.6, hc =0.5, T =7, S =3, and H =5. The results of calculations of the effect of determining physical parameters ε, hc, T, S, and Н on the sizes of d and L are listed in Table 1. The analysis of the calculations and data in Table 1 allows us to make the following conclusions:

An increase in the height of rise due to capillary forces in the soil, and the pressure in the pool, as well as the decrease in the evaporation intensity, the layer thickness, and the tongue lengths result in decreasing value of d, i.e., to an increasing ordinate of point D of the exit of the depression curve from under the tongue. For example, according to Table 1, an increase of 4.5 times in the parameter ε corresponds to a variation by 4.7 times in depth d. The value of L of the fluid-spread width over the confining bed increases with the static height of the capillary rise of groundwater, the layer thickness, and the pressure in the pool and with a decrease in the evaporation intensity and the tongue lengths. For example, it can be seen from Table 1 that the width L increases three times with increasing parameter ε 4.5 times. If we introduce the dimensionless value of $h(d)=\frac{s-d}{d},h(s)=0$, describing the relative height of the groundwater rise behind the tongue for all calculation variants, it proves that d >0 and, hence, 0< h<1, the highest and lowest values of h are achieved precisely with the variation of evaporation intensity:

maxh(d) =0.95 at ε =0.2 and minh(d) =0.01 at ε =0.9.

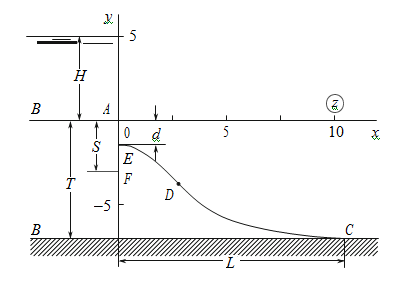
Figure 1 Flow pattern calculated at ε=0.6, h =0.5, T=7, S =3, H =5.

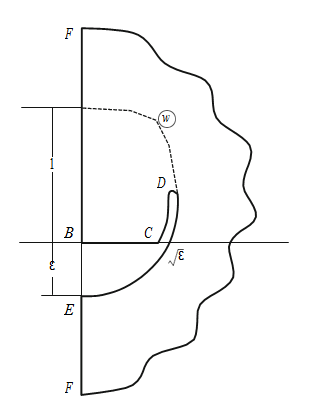
Figure 2 Region of complex velocity w for Scheme 1.

We consider now another limiting case arising in the problem of flow around the Joukowski tongue, when the soil layer is spread under an easily penetrable confined water-bearing horizon ВС, the pressure in which has a constant value of H0, and there is a uniform infiltration of intensity $\epsilon (0\le \epsilon <1)$ on the free surface (Figure 3). Then far from the tongue (at$х\to \infty$), the depression curve is horizontal and located at the height H0 above the water-bearing horizon. In this scheme, boundary conditions (1) on the portions АВand ЕАare retained, and the conditions on the boundaries ВС and CDE are replaced with the following:

$\text{BC: y = -T, }\phi {\text{ = -H}}_{\text{0}}$ $\text{CDE: }\phi \text{ = -y-T, }\psi \text{ = }\epsilon x+Q$ (7)

The region of complex velocity w corresponding to boundary conditions (1) & (7), which represents a circular triangle with two right angles and with a cut with the vertex at the point D, is shown in Figure 4. Similar polygons are quite typical in the drainage problems¹¹⁻¹³ under the motion of groundwater through dams with diaphragms,^14,15 etc., for example,.^2,3 Usually such regions are transferred into rectilinear polygons with the help of inversion with the subsequent use of the Christoffel-Schwarz formula, which, as a rule, results in the solution through elliptical functions and integrals. Contrary to these possibilities, we propose below away based on the direct use of an equation of the Fukstype, the integrals of which are the trigonometric functions sine and cosine. For this purpose, it is convenient this time to choose a different correspondence of points in the upper half-plane$\zeta$:

$-\infty ={\zeta }_D<{\zeta }_E=0<{\zeta }_A<{\zeta }_B<{\zeta }_C=1<{\zeta }_D=\infty$

Applying the Polubarinova Kochina method, we find that, in this case, the functions $\frac{d\omega }{d\xi }$ and $\frac{dz}{d\xi }$ are the linear combinations of two branches of the following Riemann function:^2,7

$P\left\{\begin{array}{cc}\begin{array}{ccccc}0& {\zeta }_A& {\zeta }_B& 1& \infty \\ -1/2& -1/2& -1& -1& 2\\ 0& -1/2& -1& -1/2& 4\end{array}& \zeta \end{array}\right\}=\frac{\text{Y}}{\left({\zeta }_B-\zeta \right)\left(1-\zeta \right)\sqrt{\left({\zeta }_A-\zeta \right)}}$ $Y= P\left\{\begin{array}{cc}\begin{array}{ccc}0& 1& \infty \\ 0& 0& -1\\ 1/2& 1/2& 1\end{array}& \zeta \end{array}\right\}$ (8)

From consideration of the region of w and relation (8), it follows that the points $\zeta ={\zeta }_B$and $\zeta ={\zeta }_A$are the ordinary points for the function Y representing the last Riemann symbol. The linear differential equation of the Fuks class with three regular special points corresponds to it:

$\zeta (1-\zeta )\text{Y ''}+(\frac{1}{2}-\zeta )\text{Y'}+\text{Y}$ (9)

Equation (9) is the Gaussian equation.⁷ Its canonical integrals in the vicinity of the point $\zeta$ = 0 are expressed through the hypergeometrical function $F(\alpha ,\beta ,\gamma ,\zeta )$⁷ and have the following form in this case:

${\text{Y}}_{\text{1}}\text{(}\zeta )=F(-1,1,1/2,\zeta )$

${\text{Y}}_{\text{2}}\text{(}\zeta )=\sqrt{\zeta }F(\frac{-1}{2},\frac{3}{2},\frac{3}{2},\zeta )$ (10)

${\text{Y}}_{\text{1}}=\text{sin2t}$ ${\text{Y}}_{\text{2}}=co\text{s2t}$ (11)

$\frac{d\omega }{dt}=-\epsilon M\frac{\text{sin}2f\text{ sin}2(t-m)}{\text{sin}2m\Delta (t)}$

$\frac{dz}{dt}=iM\frac{\text{sin}2(t-f)}{\Delta (t)}$

$\Delta (t)=(si{n}^{2}b-si{n}^{2}t)cost\sqrt{si{n}^{2}a-si{n}^{2}t}$  (12)

$\text{tan2mcot2f = }\epsilon$  (13)

Unknown constants a, b, m, and М are determined from the set of equations consisting of the expressions for S, Т, Н, H0, and with fixation of the abscissa xC of the point С of the depression curve. We note the limiting case of the flow related to the absence of infiltration, i.e., at ε=0. With taking into account the parameters m, f, and ε from Eq. (13), the solution of the problem in the case when ε=0 follows from dependences (12) at m=0, i.e., when the points С and Е of the depression curve in the plane w merge at the origin of coordinates with the point М of zero velocity. Thus, we obtained the solution of the problem considered for the first time by V.V. Vedernikov¹³ but only with another method and in a different form, i.e., through conventional trigonometric functions. In Figure 3, we show the flow pattern calculated at ε = 0.6, T=7, S=3, Н=7, H0=3, and xC=100. The results of calculations of the effect of the determining physical parameters ε, S, Н, and H0 on the value of d and the parameter h(d) are listed in Table 2 (the negative values of d mean that the free surface rises behind the tongue above the abscissas abscissa axis). The analysis of calculations and data in Table 2 enable us to make the following conclusions. An increase in the intensity of infiltration and pressure in the pool and in the underlying horizon, as well as a decrease in the layer thickness and the tongue length, result in decreasing value of d. We recall that, previously in Scheme 1, a decrease in the evaporation intensity, on the contrary, resulted in similar behavior of the value of d. From Table 2, it can be seen that it is exactly the infiltration on the free surface that induces the greatest effect on the depth d, it being quite substantial that the value of d varies almost 84 times with increasing the parameter ε 4.5 times. Contrary to Scheme 1, where only positive values of d were observed, here it proved that d< 0 for the overwhelming majority of the calculation variants, i.e., the depression curve rises above the abscissa axis and, hence, h(d) >1. In this case, the values of the parameter h can be quite significant: from Table 2, it follows that h(d)=4.91 for S=1. It can be seen that, as in scheme 1, the lowest value of h is achieved now upon variation of the infiltration intensity ε on the free surface: minh(d)=0.98 at ε=0.2.

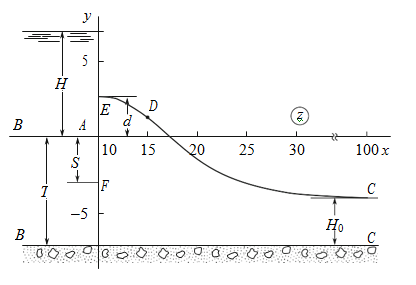
Figure 3 Flow pattern calculated at ε =0.6, Т=7, S =3, H=7, H0 =3, and xC =100.

Figure 4 Region of complex velocity w for Scheme 2.

None.

Authors declare there is no conflict of interest in publishing the article.

1. Joukowski NE. Infiltration of Water through Dams. Gostekhizdat, Russia; 1950.
2. Ya Polubarinova P. Theory of Motion of Soil Waters. Gostekhizdat, Russia; 1977.
3. Ya Polubarinova KP. Development of Investigations on the Theory of Filtration in the USSR. Nauka, Russian; 1967. p. 1−313.
4. Ya Kochina P, Bereslavskii EN, Kochina NN. Analytical Theory of Linear Differential Equations of the Fuks Class and Certain Problems of Underground Hydromechanics. Int Problems of Mechanics of the RAS, Russia; 1996.
5. Bereslavskii EN, Ya Kochina P. Some equations of the Fuchs class in hydro and aerodynamics. Fluid Dynamics. 1992;27(5):603−607.
6. Bereslavskii EN, Ya Kochina P. Differential equations of the Fuchs class encountered in some problems of mechanics of liquids and gases. Fluid Dynamics. 1997;32(5):619−625.
7. Golubev VV. Lectures on Analytical Theory of Differential Equations. Gostekhizdat, Russia; 1950.
8. Bereslavskii EN. The forcing out of saline water by fresh water during filtration from a mole irrigator. Journal of Applied Mathematics and Mechanics. 1989;53(3):350−355.
9. Bereslavskii EN. The intake of purified fresh water with filtration from a reservoir. Journal of Applied Mathematics and Mechanics. 1990;54(5):714−718.
10. Bereslavskii EN. A Hydrodynamic Model for the Forcing Back of Stagnant Salt Water by Fresh Filtration Water Flowing around a Joukowski Tongue. Dokl Phys. 1998;43(12):775−778.
11. Vedernikov VV. K Teorii Drenazha. Dokl Akad Nauk SSSR 1939;23(4):335−337.
12. Vedernikov VV. K Teorii Drenazha. Dokl Akad Nauk SSSR 1948;59(6):1069−1072.
13. Vedernikov VV. Filtracija pri nalichii drenirujushegoili vodonosnogo sloja. Akad Nauk SSSR. 1949;69(5):619−622.
14. Nelson SFB. Pritekanie gruntovyh vod so svobodnoj poverhnost’ju k sisteme dren pri glubokom zaleganii vodoupora. Izv Akad Nauk USSR. 1941;1:126−128.
15. Nelson SFB. Dvizhenie gruntovoj vody so svobodnoj poverhnust’ju cherez plotinu s dvumja diafragmami. Izv Akad Nauk USSR. 1941;3:39−44.