The objective of any pivot irrigation system is to ensure uniformity of application of water which can be achieved when responsible factors such as pressure, drop tube lengths, nozzle size etc. are adequately designed. This indoor experiment conducted in a 44m² laboratory facility tends to evaluate the extent of the influence of some sprinkler design parameters on the performance of a low pressure single pivot sprinkler spay unit. The parameters considered are; pressures of 9,12, 15 and 19Psi, nozzle sizes of 4.17, 5.56, 6.95 and 8.14 mm and drop tube lengths of 1, 1.2 and 1.5m. In this experiment an inverted U-shaped frame designed to support a spray sprinkler at different heights was used. The hydraulic installation with manual throttle valves for controlling water distribution was used to supply pressurized water to the spray model sprinkler. A number of 64 graduated catch-cans with 0.16 m diameter and 0.2m height were used. The cans were arranged in eight radial legs with a distance of 1m apart. The system was run for one hour then the caught volumes were measured manually using a graduated cylinder with a capacity of 500 mL.

The catch-cans data were used to determine uniformity coefficients. Line graphs were used to show relationships between the parameters measured. The experiment shows that there is strong relationship between the parameters considered. It indicated that the coefficient of uniformity (CU) and distribution uniformity of lower quarter DUlq increases with increase in nozzle size and pressure. It also shows that the largest nozzle size and pressure within the limits of this experiment gave the best CU and (DUlq) values of 96% and 90% at 1.5m height. Lager nozzle sizes with lower pressure reduces the CU and DUlq values. It is concluded from this experiment that though pressure, nozzle size and height of application influences the uniformity of application, larger nozzle sizes accompanied by higher pressure and height of application resulted in good uniformity of application. It is therefore imperative that while operating Pivot Sprinkler systems, careful selection of nozzle diameters, operating pressure and drop tube heights, sprinkler can be used to apply the ideal amount of irrigation water needed to refill the crop root zone that can neither cause runoff nor harm the crop and also provide the best uniformity possible under the prevailing wind and management conditions.

Keywords: heights, irrigation uniformity, nozzle size, pressure, sprinkler irrigation system uniformity coefficients

Pressure determine the performance of a sprinkler in terms of water distribution, droplet formation and radius of coverage. They are used for many purposes; soil cooling, crop production, erosion control, application of waste water and leaching.¹

To improve efficiency of water application on farms, many modern sprinkler irrigations systems have been introduced. These systems varied in design and components particularly when compared with the old systems. The most key characteristics of these systems is their ability to rationalize water consumption, improve food production and reduce environmental pollution or hazards (AFRICORP, 2021).

Center pivot sprinklers uses lower pressure during irrigation, it a completely automated system that is stationed at a point while it distributes water in a circular manner. It is composed of several components which allow it to function. The pray unit of a sprinkler contains; the nozzle, deflection plate, and the holder cover. The deflection plates allow for medium-sized droplets (say 1.5 and 4 mm) with wider throw of 8 to 12 m or more while working at low pressure (less than 200 kPa) Figure 1.²

Figure 1 Centre pivot irrigation system (Atlantis Engineering, 2012).

The objective of any irrigation system is to ensure uniformity of application of water which can be achieved when responsible factors such as pressure, raiser height, nozzle size etc. are adequately designed. These factors influence greatly the performance of the sprinkler systems.

The pressure of water controls the droplet from a sprinkler, how water is distributed and the impact of the droplet created by the pressure as influence by the nozzle size. When the pressure is very high the drop size is smaller, this can be influenced by wind during irrigation. But when the nozzle is bigger the drop size is bigger, this create bigger drop size which a high pressure can cause erosion and distant application rate from the sprinkler. According to Kranz et al.,³ sprinkler pressures can be classified as; 200 to 350 kPa as low, 350 to 500 kPa as medium, greater than 500 kPa as high pressure systems respectively.

According to Armstrong et al., (2001) the overhead impact sprinklers have a pressure range of 240kPa to 400kPa. But under low pressure operates at 276kPa, at this pressure, water jet leaving the nozzle does not break up well. This results to water application concentrating at a point. Again, when the pressure is above 483kPa the jest becomes excessive, resulting to misting formation and application is near the sprinkler.⁴ The pressure of operation tells the diameter of wetting and the atomization as depicted in Figure 2.³

Figure 2 Effect of pressure on droplet size and wetted diameter. (Source: Kranz et al, 2015).³

The level of placement of a sprinkler during irrigation has significant impact on the irrigation performance. Faci et al.,⁵ revealed that the increase in height of a sprinkler gives a smoothening and wider spread of water distribution. According to him, when the height is increased, the distance of throw is longer and that the opportune time for wind effect to evaporate and drift water droplet increases. At lower height runoff and low infiltration can results.

According to some researchers the spray droplet size at any distance from the sprinkler is related to the nozzle size (Kohl, 1974).^6–11 Kincaid et al.⁷ reported that at a stationary working pressure, the mean atomized diameters of a grooved-plate sprinkler nozzle increased when the nozzle size increased. Again the researchers stated that, with spray heads, drop sizes are influenced more by the size of nozzle rather than the operating pressure. Kohl and DeBoer⁹ detected that for low pressure spray type agricultural sprinklers, the spray plate geometry or the configuration of the surface, rather than the nozzle size and operating pressure, is the overriding variable that influenced drop distribution size.

Literatures have discussed factors influencing uniformity of distribution of sprinklers mainly focusing on one or two factors among many. Hence, other of these factors need to be considered together as a combination of factors affecting uniformity of sprinklers. This research therefore evaluated the extent of interaction between Operating Pressure, Nozzle Diameter and Drop tube lengths as they affect sprinkler application uniformity.

Materials

The materials used in this research include; sprinkler pivot spray unit; different nozzle sizes of 4.17, 5.56, 6.95 and 8.14 mm and Rotator Multi-Trajectory groove, 0.5Hp surface centrifugal pump, 2m³ tank, pressure regulator, frame, catch cans, pressure gauges, stop watch and graduated can.

Study site

The experiment was conducted in a laboratory with area of 44m²at Niger State College of Agriculture Mokwa, Nigeria Figure 3. The elevation and coordinates are 88 meters and 9°16’60” N and 5°3’0” E Mokwa has the following weather conditions; Annual rainfall of between 1000mm to 1,200mm. 32 ˚C, in March and June. Minimum temperatures of between 21 - 23⁰C in December and January. The dry seasons commences in October.

Figure 3 Map of Niger State Indicating the Study Area.

Methods

Experimental set up

The experiment was set up at Niger state College of Agriculture Mokwa, Laboratory. Carrying out an experiments in laboratory guarantees unhindered distribution of water and evades water drift and losses.^12,13

In setting up the experiment, a u- shaped frame was designed as a support for the sprinkler, this is to enable adjustment of sprinkler height. To supply pressurized water, during the hydraulic installation. A manual throttle was used to control water distribution as shown in Figure 4.

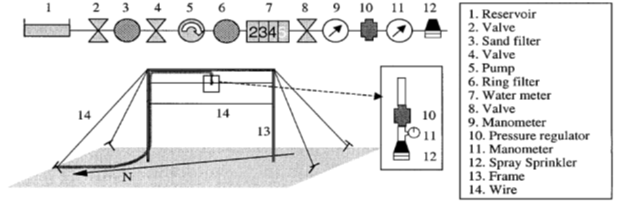
Figure 4 Structure and Components of Experimental Setup for Evaluation of Water Distribution of Individual Spray Sprinklers.⁵

The frame was built with three 50-mm-diameter metallic cylindrical bars to allow for a regulating height from 1.5 to 2 m beyond the floor and 4m wide.

The corners of the frame were fastened to the soil using four steel wires. In addition, two horizontal wires were used on the frame, this is to avoid spray sprinkler vibrations and to allow the fixing of the spray sprinkler at a 1.0, 1.2 and 1.5m height above the floor surface.

Hydraulic system

The design and construction of the hydraulic system consisted of using the followings; water reservoir with a capacity of 2m³, a 0.5Hp electric centrifugal pump, a main pipe of one and half inch PVC (25.4-mm) of 6 m long, control valve, pressure regulator, flow rate meter and low pressure pivot sprinkler spray unit. The main pipe is connected to the pump which runs to the drop tube holding the sprinkler as shown in Figure 4. Different operating pressures and nozzle diameters of (9, 12, 15 and 18 Psi) and (4.17, 5.56, 6.95 and 8.14 mm) respectively were selected. Different drop tube lengths of (1, 1.2 and 1.5m) and a Rotator Multi-Trajectory groove were also selected for evaluation Volumetric water meter was used in measuring the pressure – discharge relationship, this is to precisely control the working pressure of the nozzle. Pressure regulars of 9, 10, 15 and 20Psi were used to modify the pressure to the needed testing pressures.

Experimental conditions

In this study a low pressure pivot rotating sprinkler with grooved plate was used. During the experiment, the preferred working pressure was held fixed for each test. This was by setting a manual throttle valve before the start of data collection. Four operating pressures were used for the purpose of evaluating their impact on the uniformity of application. According to the Luiz et al.,¹⁴ rotating spray plate sprinklers (RSPS) are usually operated with a pressure of between 10 and 50 psi. Consequently, operating pressures of 9, 12, 15, 18, psi were selected in this study. Sprinkler system pressure was measured at the base of the sprinkler head using a pressure gauge having a pressure range of 0 to 87Psi and accuracy of 0.4% tolerance. Flow rate was measured with a flow rate meter.

To determine the flow rate, flow meter was used and the readings were confirmed by spot checks using weighing containers and a stop watch. Volumetric method was also used. This is to confirm the accuracy of the readings. This was done under steady conditions. Water and air temperatures were noted. In order to standardize the flow and pressure of the rotating sprinkler used for a few minutes before the experiment commences.

Catch can measurements

The indoor test was conducted in a 44m2 laboratory facility using catch-can method. Sixty-four calibrated catch-cans having 0.16 m diameter and 0.2m height were used. The cans were arranged in eight radial legs with a distance of 1m. The system was operated for one hour, and then the caught volumes were measured manually using a graduated cylinder with a capacity of 500 mL. The catch-cans data were applied to get coefficients uniformity. The test time was half an hour. Performing test for sprinkler in laboratory allows for water distribution and prevents water drift and loss (Dukes, 2006).^12,13

Calculation of coefficient of uniformity and distribution uniformity lowest quarter

Coefficient of uniformity

Equation 1 was used to determine the coefficient of uniformity

$CU=100\left[1-\frac{{\displaystyle \sum X}}{mn}\right]$   (1)

Where: CU: Coefficient of uniformity (%); m: Average volume of water collected (mm); n: number of total observations; x: deviation of individual observation from the mean (mm).

Distribution uniformity of lowest quarter

In determining Distribution Uniformity of Lowest Quarter (DUlq) which is the ratio of the mean of the lowest one over four of measurements of irrigation water used to the total mean measurement of irrigation water supplied. This is represented mathematically as equation 2;

$D{U}_{lq}=\frac{Low quater average measurement}{Overall Average Management}\times 100$   (2)

The result of the experiment conducted to test for the coefficient of uniformity and Distribution Uniformity Lowest Quarter are presented below. Figure 4 and 5 presents CU and DUlq as affected by pressure and riser height for 4.17 mm nozzle size respectively.

Figure 5 CU vs pressure for nozzle 4.17 mm.

With nozzle size of 4.17mm the CU increased with increase in pressure with h2 (1.2m) and h3(1.5m) having the highest CU of 65 and 73% respectively at pressure of 18Psi. This indicates that the CU at the tested nozzle size, pressure and height were not efficient as CU of 90 to 95% are more appropriate by standard.¹⁵

Also the figures depict CU, DUlq relationship as affected by pressure and nozzle diameter. CU and DUlq values were low. Coefficient of uniformity (CU) increases as the pressure increases. CU values were low with the drop tube length of 1m for the pressures 9 Psi and 12 Psi, then it increased rapidly when the pressure increased to p2 and p3. CU values at p1 (39%) and p2 (40%) were low as compared to p3 (62%) at h2 (1.2m). With h3 (1.5m) CU values at p1 were low (18%) but at p2 (15psi) and p3(18psi) the values were higher, 50 and 73% respectively. Figure 5 shows that the DUlq increased as the pressure was increased. DUlq values were low with the drop tube h1 for the pressures 9 and 12psi, it then increased with the increase of the pressure. The higher DUlq values were achieved with drop tube of 1.5 m and this shows that with small nozzle when height increases water can be distributed at farther distance and this improves the DUlq consequently increasing area under irrigation. This result is similar to that of Manal et al.¹⁶

The coefficient of uniformity and distribution uniformity of lower quarter under varying pressures and drop tube lengths for nozzle size 5.56 mm are shown in Figure 6 and 7 respectively. The coefficient of uniformity raised with increase in pressure, nozzle size and height. The CU at the height of 1 (h1) and 1.2 m (h2) were higher at the pressure of 18 Psi. The values of 75, 83 and 91 % attained for CU at p3 for h1, h2 and h3 and nozzle 0f 5.56mm were in the range of good CU. According to Hussein and Ahmed (2021) good CU values for Pivot systems should be within the range of 74 to 90%.

Figure 6 DUlq vs pressure for nozzle 4.17 mm.

The higher values of CU were achieved at h2 followed by h1 and then h3. Figure 7 shows that with the nozzle size of 5.56 mm DUlq increased as the pressure was increased. The values of DUlq were higher with drop tube length of 1m and lower with the drop tube length of 1.5m which might be related to possible interference of wind and lighter drop sizes and this coupled with the combination of longer throwing led to increase in water losses. Consequently, DUlq values decreased.

Figure 7 CU vs pressure for nozzle 5.56 mm.

Figure 8, 9 shows the interaction between nozzle size 6.95mm and h1, h2, h3 with p1, p2, p3 as they affect CU and DUlq. It depicts that nozzle size 6.95mm with the combination of the experimental pressures and heights gave similar trends for both CU and DUlq. This is also similar to the results of (Etefa and Minda, 2022).¹⁷ Figure 10, 11 depicts the CU and DUlq values as they relate to h1, h2, h3 and p1, p2 and p3 for nozzle 8.14mm.

Figure 8 DUlq vs pressure for nozzle 5.56 mm.

Figure 9 CU vs pressure for nozzle 6.95mm.

Figure 10 DUlq vs pressure for nozzle 6.95 mm.

Figure 11 CU vs pressure for nozzle 8.14 mm.

For the nozzle size 8.14mm the CU was highest with 96% at the pressure of 18Psi and height of 1.5m followed by the height of 1m with CU of 80% at the pressure of 15Psi. This means that higher pressure with bigger nozzle diameter improve CU and DUlq. Also lower pressure with bigger nozzle diameter reduces CU and DUlq as seen in p1for h1, h2, and h3 with CU value of 40, 61, and 69% respectively. This can also be seen for DUlq values at p1 for h1, h2, and h3 as 13, 26 and 44%. This is similar to the findings of (Manal, et al., 2014).¹⁶

Therefore, Figure 10 shows that with the nozzle 8.14 mm, CU increased as the pressure was increased. The higher values of CU were achieved with the drop tube 1.5m. The lower values of CU were with the drop tube length of 1.2m. Figure 12 shows that with the nozzle 8.14 mm, DUlq increased as the pressure increased. The higher values of DUlq were with the drop tube 1.5m and the lower DUlq values were with the drop tube 1.2m. This implies that higher drop tube length at 1.5m supports DUlq. This result is similar to that of (Kuti et al., 2019).^18–30

Figure 12 DUlq vs pressure for nozzle 8.14 mm.

It is concluded from the above experiment that:

1. Nozzle size, pressure and sprinkler height have interacting influences on the trajectory and uniformity of a given sprinkler droplet.
2. The uniformity of application of a grooved-plate sprinkler with larger nozzle sizes increased as the pressure and height increased.
3. Drop sizes were more affected by the nozzle size instead of the working pressure.
4. Careful selection of nozzle diameters, operating pressure, drop tube lengths, can be used to apply the required quantity of irrigation water necessary to fill-up the crop root zone. This will take care of runoff, provide the required uniformity under prevailing wind and management conditions.

None.

The author declares there is no conflict of interest.

1. Dana P. Irrigation for Small Farms. 2016. p. 1–60.
2. Allen RG. Irrigation Engineering Principles. Department of Biological and Irrigation Engineering, Utah State University, Logan, Utah. 2003.
3. Kranz WL, Evans RG, Lamm FR, et al. A Review of Mechanical move sprinkler irrigation Control and automation technologies. ASABE Engineering a Suitable future. 2015.
4. King BA, Kincaid DC. A variable flow rate sprinkler for site-specific irrigation management. Applied Engineering in Agriculture. 2004;20(6):765–770.
5. Faci JM, Salvador R, Playan E, et al. Comparison of fixed and rotating spray plate sprinklers. J Irrig Drain Eng ASCE. 2001;127(4):224–233.
6. ASAE Standards. S330.1 Procedure for sprinkler distribution testing for research purposes. 32nd edn. St. Joseph, Mich., ASAE. 1985.
7. Kincaid DC, Worstell RV, Kemper WD. Automated Cable Control Irrigation System. In: Proc. Irrig. Assoc. Techn. Conf. 1982/02. 1982. p. 242–255.
8. Kincaid DC, Heermann DF, Kruse EG.  Application rates and runoff in center pivot sprinkler irrigation. Trans. ASAE 12:790-794, 797. 1969.
9. Kohl KD, Kohl RA, DeBoer DW. “Measurement of low pressure sprinkler evaporation loss.” Trans ASAE. 1987;30(4):1071–1074.
10. Pawlak K, Kołodziejczak M. The role of agriculture in ensuring food security in developing countries: Considerations in the context of the problem of sustainable food production. Sustainability. 2020;12(13):5488.  
11. Sharma N. Chapter-5 Ways of Nutrition Security. Nutrition and Food Science, 2022. p. 65.
12. Sourell H, Faci JM, Playan E. Performance of rotating spray plate sprinklers in indoor experiments. Journal of Irrigation and Drainage Engineering. 2003;129(5):376e380.
13. Liu JP, Yuan SQ, Li H, et al. Numerical simulation and experimental study on a new type variable-rate fluidic sprinkler. J Agric Sci Techol. 2013;15(3):569–581.
14. Luiz RS, Antonio PD, Tarlei AB. Performance of an Iris Mechanism Equipped with Fixed and Rotating Deflector Plates for Variable Rate Sprinkler Irrigation. J Irrig Drain Eng. 2019;145(12):04019027.
15. Dong Y, Kelley L, Anderson E. Demonstration of Center Pivot Uniformity Evaluation and Retrofit to Improve Water Use Efficiency. Journal of Water Resource and Protection. 2023;15:71–84.
16. Manal O, Suhaimi BH, Khamaruzaman BWY. Effect of low pressure on irrigation uniformity of solid set sprinkler irrigation system. Applied Mechanics and Materials. 2014;567(2014):26–31.
17. Etefa TA, Minda TB. A Review on Factors Affecting the Uniformity of Sprinkler Irrigation. Journal of Engineering and Applied Sciences. 2022;7(5):71–76.
18. Kuti IA, Ewemoje TA, Adabembe BA, et al. Effect of Different Riser Heights on Sprinkler Irrigation Performance Under Constant Operating Pressure. AZOJETE. 2019;15(1):124–132.
19. Atlantis Engineering. Atlantis. 2012.
20. DeBoer DW. “Drop and energy characteristics of a rotating sprayplate sprinkler.” J Irrig Drain Eng. 2002;128 (3):137–146.
21. Etefa TA, Minda TB. A review on Factors Affecting the Uniformity of Sprinkler Irrigation. Journal of Engineering and Applied Sciences. 2002;7(5):71–76.
22. Hussein A, Ahmed ZD. A Comparative Study of Standard Center Pivot and Growers-Based Modified Center Pivot for Evaluating Uniformity Coefficient and Water Distribution. Agronomy. 2021;11:1675.
23. ISO 7749-2. Agricultural irrigation equipment—rotating sprinklers—part 2: uniformity of distribution and test methods. International Standards Organization. (1990), MOD GB/T 19795.2. 2005.
24. James GL. Principles of Farm Irrigation System Design”. 1st edn. Johan Wiley and Sons, Inc., New York, USA. 1988.
25. Junping L, Xingye Z, Shouqi Y. Hydraulic Performance Assessment of Sprinkler Irrigation with Rotating Spray Plate Sprinklers in Indoor Experiments. Journal of Irrigation and Drainage Engineering. 2018;144(8).
26. Michael AM. Irrigation: Theory and Practice. Vikas Publishing House. PVT.LTD. New Delhi, India. 1999.
27. Moore S, Young JH, Niyazi B. Instrumentation for variable‐rate lateral irrigation system. ASABE Paper No. 052184. St. Joseph, Mich.: ASABE. 2005.
28. USDA-NASS. Table 4: Land irrigated by method of water distribution, 2008 and 2003. In Census of Agriculture: 2008 Farm and Ranch Irrigation Survey. Washington, D.C.: USDA National Agricultural Statistic Service. 2009.
29. Valley-Standard. Valley West Irrigation Inc. 50. Saskatchewan Rd. Outlook, SK Sol 2No., 1998.
30. Valeria L, Claudia K, Bruce S, et al. Improved water management using subsurface membrane irrigation during cultivation of Phaseolus vulgaris. J Agric and Res Econ. 2019;23(2):401–426.