The least squares method has been largely used in several areas, mainly because of its simplicity. It is a widely used knowledge tool. However, the current advances in Information Technology have contributed to the development of decision support systems, in a search for greater reliability of predictions from samples. The use of Information Technology in Limnology is still limited. The main objective of this study is to show the possibility of using Artificial Neural Network in the process of inference of the total number of the rate of biological communities from samples. Our data show that the use of nonparametric inference, along with nonlinear data mapping, may lead to more consistent and efficient results, as the Artificial Neural Networks.

Keywords: species richness, diversity index, biological communities

Ecologists characterize biological communities according to the number of species present in the environment, their relative abundance, and their trophic and ecological relationships. The structure and functioning of communities present a complex set of interactions, directly or indirectly uniting all community members into an intricate web.^1,2

To characterize biological communities, researchers make use of several indices and parameters. There are various diversity indices, and each of them tries to describe the diversity of a giving community by means of just one number.^3,4

The least squares method has been largely used for different purposes, mostly due to its simpleness. Nonetheless, the current advances in Information Technology have contributed to the development of decision support systems, in a search for greater reliability of predictions.⁵

Sampling and data analysis are the first steps in environmental studies. In case any of those steps fails, all woks will be compromised, as well as the eventual correction, management, or environmental management programs.^6,7 Hence, Artificial Neural Networks may be a good tool in these studies, since they are able to describe the relationship between variables involved in the process, providing a better data analysis. The analysis generates greater productivity, reliability and quality estimates and predictions. The use of information technology in Limnology is still limited, including biological community richness estimates.

Thus, the objective of the present study was to assess the possibility of using Artificial Neural Networks to infer the total number of taxa in biological communities.

Artificial substrates placed on the riverbed of Uberaba River in Minas Gerais were used as a study model. They were used to sample benthic macroinvertebrates. The artificial substrates were composed of 200 grams of previously washed gravel, packaged in sacs made of 80% shade net placed on the riverbed to sample macroinvertebrates (Figure 1). The samples were taken after 15 days of exposure. The experiment was performed with nine replicates.

Figure 1 The site used for sampling benthic communities in Uberaba River, in Uberaba/MG.

After being sieved through a 0,30 mm lower sieve, the material was fractioned into two portions. One portion corresponded to the material retained on the 500 µm mesh, and the other portion corresponded to the material retained on the 300 µm mesh.

Several methods have been used to assess the total biological community richness from samples.^8,9,10

The simplest formulation of least squares used to explain the relationship between independent variables and the dependent variable, through traditional methodology, is represented by the following equation:

Y_i = β₀ + β₁ X_i1 + β₂ X_i2 +...+ β_k X_ik + ε_{i ,}           i=1,..,m          (1.1)

where:

Y₁ ,...,Y_m – is called dependent variable and is represented by the number of taxa in the different meshes and in the whole community;

X_i1,..., X_ik – are called independent variables. Only one independent variable was used in our study, corresponding to the number of sampling used;

β_0,..., β_k  -  are called model parameters, and

ε_i,...,ε_m – are the random errors that cannot be explicitly explained. They are caused mainly by the variations in the measurement done in field.

The equation (1.1) can be written in matrix notation as:

Y = Xβ + ε,            (1.2 )

Being:

Y, β, and ε  respectively, the vectors of observed taxa, parameters, and random errors of the regression model, and

X the matrix of the independent variable observations

Parameter estimation is made by statistical inference based on a representative sample of the analyzed segment. Traditionally, these estimations have been made using the Ordinary Least Squares (OLS) method, consisting of minimizing the sum of the squares of the distances, vertically measured, between the observed values and the values adjusted by the adopted model. The model coefficient vector is obtained by:

b = (X’X)^-1(X’Y).  (1.3)

Therefore, the estimated average value for a sampling, with characteristics represented by a vector C = [ 1 c₁ c₂  ...  c_k ], based on a model with k independent variables and estimated parameters vector b = [ b₀ b₁ b₂ ... b_k ]’, is calculated by the expression:

Yc = Cb (1.4)

With the intention of having unbiased, efficient, and consistent parameters inferred by the ordinary least squares (OLS) method, some assumptions concerning the independent variables, the residuals and the model specification must be observed. These assumptions include: the independent variables should not have any random disturbances, nor should exist any linear relationships between them; random errors must comply with the constant variance hypothesis (homoscedastic model), normality and absence of autocorrelation; the model should be correctly specified, that is, only relevant explanatory variables should be included in its composition, and the range of the involved variables should be properly chosen, with the aim of ensuring the model linearity. This model is named Classic Regression Model (CRM)

The artificial neural network (ANN) used in the current study (SisReN^® software – Artificial Neural Network and Linear Regression System) is a multilayer network. The type of learning selected for this network typology is known as monitored learning based on the “back-propagation of errors” system. These networks use two or more processing neuron layers.

The input layer (sample number) receives the external inputs, whereas the output layer (species richness) is responsible for generating the network answer. In this study, we have a third layer between the two layers previously mentioned, which is named hidden layer and is composed of three neurons. The linear function was used in the network’s output, and the hyperbolic tangent was employed in the hidden layer.

For each standard set, the network weights are adjusted to minimize the difference between the network outputs and the desired ones. Error is minimized by using the gradient technic with a convergence factor called learning rate. The only requirement for the considered network type is that the input and output values meet in the 0 to 1 interval by compatibility with the transference function.

The macroinvertebrate community presented a total of 37 taxonomic categories in the nine samples analyzed. Two protozoans provided with theca were related, as well as two taxonomic categories of Gastropoda and Crustacea. For the classes Hydrozoa, Turbellaria, Oligochaeta, and Arachnida, and for the subclass Hirudinea only one taxonomic category was related. Insecta was the most abundant group, with seven Orders and 26 taxa (Table 1).

Tables 2 and 3 show sub-samples of the whole community. Both sub-samples consist of parcels retained on sieves of different meshes. The differences were relatively small. Only a few taxonomic categories were exclusive of a given sieve.

Three taxonomic categories were exclusive of 300 µm mesh: Rhizopodea 2, Copepoda e Ceratopogonidade; whereas 11 categories were exclusive of 500 µm mesh: Physidae, Hirudinea, Tricorythidae 1, Libellulidae, Corduliidae, Calopterygidae, Perlidae, Naucoridae, Helicopsychidae, Gyrinidae, and Psephenidae.

Although the fraction larger than 300µm and smaller than 500µm is responsible for a total number of taxa relatively small, when this is considered, the trend towards stabilization tends to be shown at an earlier point, and three new taxa are observed.

Figure 2, 3 and 4 show the taxa cumulative curve in each sample fraction and in the total sample.

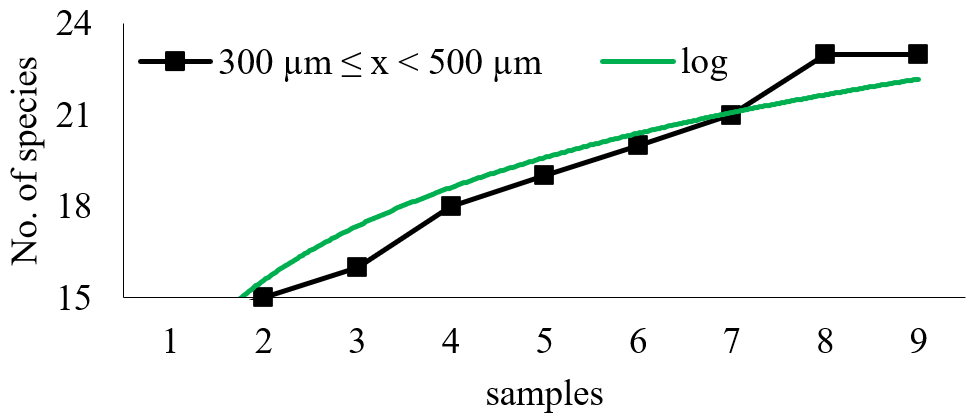
Figure 2 Cumulative curve of the total number of taxa observed in the retained fraction between 300 e 500 µm (R² = 0.9121).

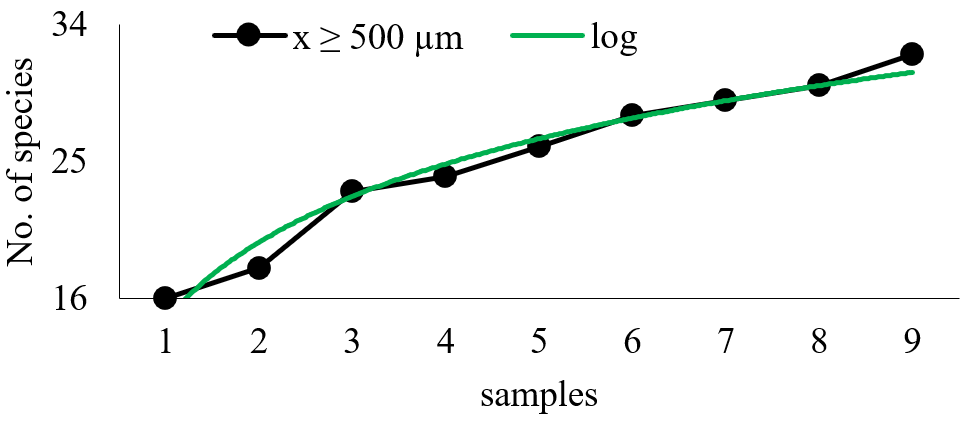
Figure 3  Cumulative curve of the total number of taxa observed in the retained fraction using 500 µm mesh (R² = 0.9688).

Figure 4 Cumulative curve of the total number of taxa observed in the total sample (R² = 0.9506).

The logarithmic functions inserted in each case present high R² values, indicating that a great part of the initial variation in the arithmetic mean can be explained by the sampling number introduction in the equation. It is important to emphasize that the introduction of the logarithmic transformation into the independent variable is meant to provide a solution that aims to a dependent variable stabilization in relation to the independent variable increase. Although this transformation shows a stabilization trend, it has generated an equation with an adjustment smaller than the data without transformation. The equation for the fraction retained on the 300 µm mesh was: y = 4.3928 Ln(x) + 12.529; with R² = 0.9121; indicating that 91.21% of the observed data variation is explained by the equation. The equation for the fraction larger than 500µm was y = 7.2277 Ln(x) + 14.719; with R² = 0.9739. For the whole community, the cumulative curve of new taxa has had 92.99 % of its variation explained by the function y = 6.7036 Ln(x) + 18.465.

Figure 5 shows the cumulative curve of taxonomic groups for the two fractions and for the whole community.

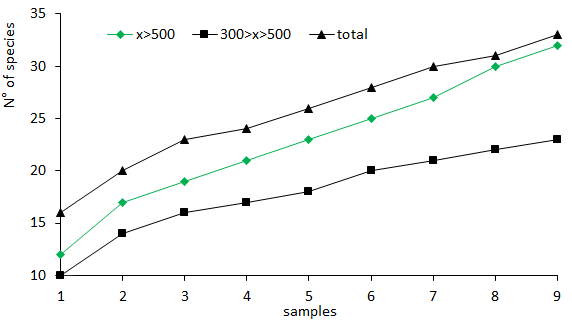
Figure 5 Cumulative curves of the total number of taxa observed in the fractions and in the total sample, in case sampling units to be initially collected showed smaller numbers of taxa.

It is worth noting that there is a trend of an increase in the number of new taxa only in the fraction corresponding to 500 µm, even after the new sample, indicating that, if only this fraction were analyzed, the total number of taxonomic groups sampled would be smaller and that the stabilization trend would be would happen later. The pattern of increase trend of new groups is not observed in the 300 µm fraction, nor in the total sample.

Though the fraction smaller than 500 µm is responsible for a total taxa number relatively small, when this fraction is considered, the trend to stabilization tends to be seen in an earlier point, and three new taxa are observed.

This type of approach is often used by other authors. However, it can compromise the result and evaluation.^3,4,7,11,12

The community sampling is a draw of individuals in a group (a random sampling). The cumulative curve stabilization, which is used as a reference of the appropriate number of sampling units which should be employed, can vary according to the order these sampling units are collected. Hence, with the data issued, according to the order of collection of these sampling units, we could have rather different results, as shown in Figure 5 and 6.

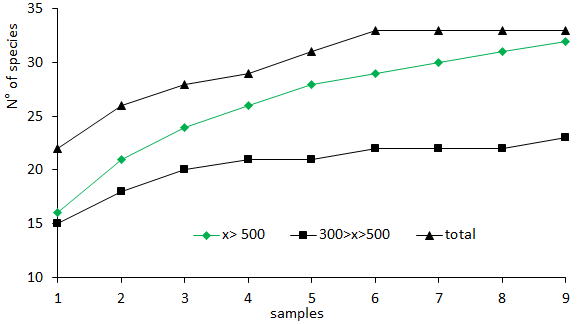
Figure 6 Cumulative curves of the total number of taxa observed in the fractions and in the total sample, in case sampling units to be initially collected, showed bigger numbers of taxa.

In case sampling started with a smaller number of taxa, we would have the logarithmic function y = 7,7544 Ln (x) + 14,748; com R² = 0.9515. In case sampling started with a bigger number of taxa, we would have the logarithmic function y = 5.6935 Ln(x) + 22.568; com R² = 0.9722.

With the presented functions, estimating the number of taxa, with ten samples, we would hypothetically have, in the first case, approximately 33 different taxonomic groups. If the sampling started with bigger numbers of taxa, we would have approximately, 36 taxonomic groups. Making a projection in case we had 100 samples, the picture would be reversed, and in the first situation, we would have 50 taxa, smaller than the 49 ones observed in the second simulation.

In routinely performed monitoring work, the reduction in the cost of analysis is associated with the reduction of the number of sampling unities. If we had made this estimate for three samples, we would have 23 and 29 taxonomic groups, respectively. These values would be estimates of a same community, demonstrating that differences could be indicated, where they did not exist, or impacts would not be detected by the analysis, when in fact, they are present. Thus, environmental managers can eventually make management decisions that are not always based on reliable data.

This exercise demonstrates the need for large samples. The 300 µm fraction is important since it makes the total cumulative curve tend to stabilize, and because this fraction has presented taxonomic groups that were not seen in fraction 500 µm, due to random events or to its size.

Figure 7 shows the ordering of the distribution of all taxonomic groups found in the sampling. The power function used in this case presents a high R² level, indicating that a great part of the observed variation can be explained by the equation. The equation is expressed by y = -7E-08x⁶ + 6E-06x⁵ – 0.0002x⁴ + 0.0015x³ + 0.0174x² – 0.4201x + 3.7667; with R² = 0.9924; showing that 99.24% of the observed data variation are explained by the equation.

Figure 7 Ordering of the distribution of all taxonomic groups found in the sampling.

A similar analysis could have been performed with the aid of Artificial Neural Network – (ANN). Lately, ANN has been put into sharp relief in scientific communities as a result of its modeling capacity when data are not linearly related.

Artificial neural networks have high potential for applications in ecology and, specifically, in modeling biological communities. However, lack of information is a frequent problem that needs to be addressed to overcome limitations.^13,14

The (ANN) used in this work is a multilayer network. The kind of learning selected for this network typology is known as supervised learning based on the backpropagation of errors system.

These networks use two or more processing neuron layers. The input layer receives the external inputs, whereas the output layer is responsible for generating the network answer. In this study, we have a third layer between the two layers previously mentioned, which is named hidden layer. The choice of the network complexity, that is, the number of layers chosen and the number of neurons in these layers, follow some empirical criteria. The network used in this work has one input layer with only one variable (number of sample), an intermediate layer composed of three neurons, and an output layer, which represents the number of taxa retained on the studied mesh.

The structures chosen for the sampled data training differ in their nature in relation to the number of neurons in the hidden layer. In the structures used, the number of neurons in the hidden layer was 3, corresponding to 2(N+1), where N is the number of input variables. The number of neurons in the output layer is 1, corresponding to the number of network outputs.

This ANN type back-propagation of errors was trained by means of supervised learning. The process employs the sampling collected data pattern, which are provided at the network input. The results obtained are compared with the desired output, which was the number of taxa observed for each sampling. For each standard set/pattern set, the network weights are adjusted to minimize the difference between the network outputs and the desired ones. Error is minimized by using the gradient technic with a convergence factor called “learning rate.”

The greatest effort in training a neural network usually consists of collecting and pre-processing data. Pre-processing comprises the input and output data normalization. For the network type considered, the only requirement is that the input and output values lie in the interval 0 to 1, by compatibility with the transfer function. We have adopted procedures aimed at normalizing the input data related to their corresponding outputs before using them in the Artificial Neural Networks training.

With the purpose of feeding the ANN training process, we have utilized the collected data listed in Table 1. The training, which was performed by the backpropagation of error process, using 2,000 epochs, at 0.15 learning rate. We have developed an MLP (multilayer perceptron) network consisting of three neurons in the hidden layer. The linear function was used in the output network, and the hyperbolic tangent, in the hidden layer. The ANN analysis has indicated a total number of 34 taxonomic categories in the benthic macroinvertebrate community.

Neural models provide a bridge between learning and ecological modeling; providing a new step in data analysis, with inferential capacity in biological communities.^15,16

According to the more conservative methodology, the total number of taxonomic categories would be around 23 to 36, with a great error margin, depending on the sampling effort. In contrast, using the ANN methodology, the exact number would be 34, a value close to the average, in case a bigger sampling effort performed was high. We obtained the attribute estimation of a biological community using neural networks. This approach can provide an important tool for managing natural resources.^13,17

The parametric inference process performed by the least squares has shown logarithmic functions with high R² values, indicating that a large part of the initial variation around the observed arithmetic average can be explained by introducing the sample number in the equation.

The cumulative curve stabilization can vary according to the order the sampling units are collected, determining thus, different results. When data relate to each other in a nonlinear way, the Artificial Neural Networks indicate the exact value in a more precise and accurate manner due to their modeling capacity. Therefore, the Artificial Neural Network should be indicated, to the detriment of traditional methods.

None.

None.

1. Leitao MLC, Silva IL, Hiroki KAN, et al. Diferenças ecomorfológicas e funcional em populações de Phalloceros harpagos Lucinda, 2008, na bacia do Alto Rio Paraná. Biota Amazônia. 2018;8:34–38.
2. Souza F, Leitao MLC, Rocha BGA, et al. Estrutura Ictiofaunística do Rio Uberaba: A Influência dos Barramentos na Dinâmica Ecológica das Comunidades de Peixes. Biota Amazônia. 2016;6:87–93.
3. Pelli A, Teixeira MM, Reis MG. Ocorrência de formigas em uma área urbana peri-hospitalar de Uberaba/Brasil. SaBios (Faculdade Integrado de Campo Mourão. 2013;8:107–113.
4. Quina CL, Pelli A, Martins AGC. Sucessão de macroinvertebrados bentônicos em carcaças de rato no Rio Uberaba - MG. SaBios (Faculdade Integrado de Campo Mourão). 2013;8:73–80.
5. Nascimento J, Macedo M. Modelagem de Equações Estruturais com Mínimos Quadrados Parciais: um Exemplo da Aplicação do Smart PLS® em Pesquisas em Contabilidade. Revista de Educação e Pesquisa em Contabilidade (REPeC). 2016;10(3):2.
6. Pelli A, Oliveira AG, Silva PR, et al. Adhesive cards for monitoring flying insects in a neonatal intensive care unit in a hospital in the Triângulo Mineiro - Minas Gerais – Brazil. Biotemas. 2012;25:199–201.
7. Costa SB, Pelli A, Carvalho GP, et al. Formigas como vetores mecânicos de microorganismos no Hospital Escola da Universidade Federal do Triângulo Mineiro. Revista da Sociedade Brasileira de Medicina Tropical. 2006;39:527–529.
8. Pelli A, Barbosa FAR. Insect fauna associated with Salvinia molesta Mitchell in a lake of Lagoa Santa Plateau, Minas Gerais, Brazil. Proceedings of the International Association of Theoretical and Applied Limnology. 1998;26:2125–2127.
9. Pelli A, Barbosa FAR. Insetos coletados em Salvinia molesta Mitchell (Salvineaceae), com especial referência às espécies que causam dano à planta, na Lagoa Olhos d'Água, Minas Gerais, Brasil. Revista Brasileira de Entomologia. 1998;42:9–12.
10. Honorato GBS, Pelli A. Utilização da comunidade bentônica na avaliação da qualidade de água no Córrego Gameleira, Uberaba/MG. SaBios (Faculdade Integrado de Campo Mourão). 2011;6:15–26.
11. Reis A, Melo T, Pelli A. Sucessão de insetos em peça anatômica de galinha Gallus gallus domesticus em um córrego de Vereda em Uberaba/MG. Revista Brasileira de Ciência, Tecnologia e Inovação. 2006;1(3):1–8.
12. Pelli A, Barbosa FAR. Insect fauna associated with Salvinia molesta MITCHELL in a lake of Lagoa Santa Plateau, Minas Gerais, Brazil. SIL Proceedings. 1998;26(4):2125–2127.
13. Hadjisolomou E, Stefanidis K, Herodotou H, et al. Modelling Freshwater Eutrophication with Limited Limnological Data Using Artificial Neural Networks. Water. 2021;13(11):1590.
14. Joseph MB. Neural hierarchical models of ecological populations. Ecol Lett. 20120;23:734–747.
15. Bravata N, Kelly D, Eickholt J, et al. Applications of deep convolutional neural networks to predict length, circumference, and weight from mostly dewatered images of fish. Ecol Evol. 2020;10:9313–9325.
16. ME Kimball, RM Connolly, SB Alford, et al. Novel Applications of Technology for Advancing Tidal Marsh Ecology. Estuaries and Coasts. 2021.
17. Li J, Knapp DE, Fabina NS, et al. A global coral reef probability map generated using convolutional neural networks. Coral Reefs. 2020;39:1805–1815.