Soil infiltration has always been a significant phenomenon in hydrology so because of the importance of what happens to rainfall after precipitation and what is the percentage of the water which would be subsurface water and how much of it would be considered as runoff. So many models such as SCS of USDA soil conservation service have been presented, but some parameters such as slope, precipitation intensity, vegetation and soil grading which have not been considered in SCS model. In this paper by the means of the rainfall simulation system the curve number was assessed due to above parameters and actually a new formula has been presented due to slope, precipitation intensity, vegetation and soil grading. Within the 2% increase of the slope, the CN number amount increased 0.8% in vegetated soil and 1.15% increased in non-vegetated area and with 10% increase in the precipitation intensity , CN number decreased about 15% in both vegetated and non-vegetated area.by clay percentage deduction in soil , runoff increased 4% in both vegetated and non vegetated soil.

Keywords: curve number, clay percentage, precipitation intensity, vegetation

The science or study of water is called “hydrology”; however, modern hydrology involves assessing the movement of water over and beneath the earth.¹ Through these kind of movements in natural areas, precipitations are mostly precipitating into surface soil. Therefore, analyzing infiltration factor is important in hydrologic cycles.² Infiltration models are depended on soil types and site conditions for estimating infiltration factor involving numerical and experimental methods.³ Richard (1931) derived an equation from Darcy’s law, a law conducted by a French hydraulic engineer in 1856, and law of conservation of mass.² This equation may have errors due to lacking soil properties and analytical solution,² however Philip (1957) established infinite solution for Richard’s nonlinear equation. The first physically based infiltration process was derived by Green and Ampt (1911).² Since its’ simplicity and acceptable performance, this approach has chosen as the foundation of soil and water sciences, however the simulation of water flux estimation in this method is complex.² With considering Green-Ampt equation, Mein and Larsen (1973) determined ponding time in infiltration modeling.² The first infiltration equation based on curved fitting field data suggested by Ksotiakov.² In 1957, USDA (United Stated Department of Agriculture) developed an equation based on daily rainfall data. Smith and Parlange (1978) derived an equation with considering Richard’s equation. Parhi (2007) modified Kostiakov model, however in 2014,^4,5 Parhi revised the modified Kostiakov model to improve performance.⁶ Curve Number Model has developed by U.S. Department of Agriculture. In spite of having limitations and misinterpretations for this method, it has acceptable precision.⁷ In this model, there are several ways for precipitation to fall on land surface.⁷

1. Overland flowing excess infiltration: This process occurs when rainfall intensity exceeds infiltration capacity. In this condition, water cannot be absorbed by soil, therefore
2. Overland flowing excess saturation: Any precipitation return on surface and can add to surface runoff. This can be called return flow.
3. Shallow subsurface flow: In this condition, water flow shallowly downslope in the soil which is quickly enough to be considered as storm flow.
4. Groundwater flow: The exfiltrated water from aquifer flows to the streamflow.
5. Direct precipitation in stream surface: Any natural precipitation falls directly on surface of water.
6. Percolation: The absorbed precipitation exceeding from soil capacity which can flow downward to aquifer.

Unlike the aforementioned studies, which neglect studying parameters like slope, precipitation intensity, vegetation types and different soil grading, this study analyze runoff and precipitation penetration affecting by aforementioned parameters for 54 tests.

In this study, the soil should be preferably extracted intact, since it can influence on results accuracy. After measuring the soil with ruler, the soil weight will be measured instantly. The soil sample should be transferred to rainfall simulation tank in laboratory of Islamic Azad University, South Branch. The intact soil divided into three groups shaking with granulation devices. Group A, B and C, which each of them has different clay, amount including 29%, 0.5% and 65% respectively. As shown in Figure 1, the 64*64*20 rainfall simulation tank with seven nozzles is used to spray water on soil samples, though device’s slope can be regulated easily.

Figure 1 has different parts which is being mentioned below:

1. The latest water tank of device and specified nozzle for adjusting the level of water for device.
2. The back pitted sheet of device.
3. The internal drainage of device.
4. The water nozzles.
5. The ending pitted sheet of device for exiting water from soil sample.
6. The piezometers.
7. The main tank for providing water for system.
8. The graded sheet for piezometers.
9. The tank for gathering penetrated water from inside of device.

Figure 1 Rain simulator device and soil column.

For extracting a soil sample from the site, it would be better to have a common shape for digging, since special weight should be calculated in following stages. Although soil density is a significant factor in amount of permeability and runoff formation, retrieving the first soil density with special weight is difficult and time-consuming. The excavated volume of trench has been measured since its’ shape is rectangular, therefore the soil volume can be obtained through multiplying trench’s area to trench’s depth. Finally, the special mass can be reached by Equation 1.

$\rho \text{=}\frac{m}{\upsilon }$ (1)

While the volume of device’s soil tank is easily measurable, it what mass of become clear that the soil is in specific volume. First, the layer mass of soil released till the desired level of tank, and then when a certain mass of soil was in specific volume of device, the soil simulated in research located. Another parameter that can be raised in forming runoff is initial moisture. Obtaining to appropriate moisture requires mix up and doing some experiments regularly therefore, all experiments have been done on soil saturation condition. Therefore, have been added some water to saturating soil. A kilogram of soil without moisture that have been gotten from the oven put into scaled container that have been filled with specific level of water. According to the obtained the difference of volume, have been calculated the amount of soil’s seed (or Vs) for a kilogram of soil. And then, according to that is obvious the mass of soil inside of device, with obtained relationship calculated the amount volume of the soil’s seeds. With difference between the volume of the soil and entire volume of device that is filled by soil, obtain the amount of volume of empty-space inside of soil that must fill with this amount of water. This amount of water released gradually on the surface of the soil till obtain to the saturation soil. After that the soil sample have been ready, before, was assumed that all experiment done by rainfall intensity.

Initially, by having amount of permeability of soil and vegetation, have been read the relevant CN evaluations and secondly, have been put the achieved number inside formula and finally, according to the amount of precipitation, have been measured the amount of runoff. As it’s observed, the process of working with this model is a simple process that has tried to summarize all the effect of variables into one variable. Although this may lead to convenience of working with this model, due to fact that has been seen all of effect of variables in it, the sensitivity of his model for this number is very high and any carelessness and error in choosing it can effect on presented results by this model. Despite this model is a fairly complete one but the effect of slope of the earth isn’t directly in model calculations. In this research, the effect of the different amount of the earth’s slope, intensity of precipitation, clay precipitation (in dual mode: with and without vegetation) have been studied, on resulting runoff from precipitation in curve number model. The purpose of this research was “Determining the amount of the influence of soil grading and vegetation on the curve number model” and due to the fact that slope of the earth, kind of soil (clay percentage), type of vegetation haven’t been reviewed in this model simultaneously, therefore the effect of this variables has been used for calculation of the number of SCS curve number model. First, when the device is empty, the tap of device has been opened in sufficient amount. Then, have been measured amount of water that removed at specific time form nozzles and there by measured the depth of the water that released on the soil. And then, created the initial slop by the embedded screw at the end of the device and then the rain showered for equilibrium situation. Because of the soil is in saturated state, have been expected that the runoff form early. And because of the soil doesn’t infiltrate the added water, the soil infiltration curve is almost horizontally. After the full of system reached to equilibrium, after specific time that applied amount of desired artificial rain, measured the amount of runoff and water that moved and infiltrated inside the soil. This work has done for different slops (4%, 6%, 8%) and intensity (29.5, 35, 46.7 mm per hour) with different gradation and in two states (with and without vegetation) that have been brought the resulting curve number evaluations in Table 1‒3.

According to the outcomes of various experiments following results have been achieved.

It is shown from Figure 2 & 3 that the numbers changes of the curve number in intensity of 29.5mm/h on different slopes (4%, 6%, 8%) for various type of soil (A, B, C), based on the results excavated from graphs for specific type of soil. Equable rainfall intensity determined that changes in slopes don’t have significant impact on CN evaluations. But at equable slope with increasing the percentage of clay, CN evaluations increase significantly. It is seen from Figure 4 & 5 that the numbers changes of the curve number in intensity of 35 mm/h on different steepness (4%, 6%, 8%) for various type of soil (A, B, C), based on the results have been excavated from diagrams for specific type of soil. Equable rainfall intensity, determined that changes in slopes don’t have significant impact on CN evaluations. But at equable slope with increasing the percentage of clay, CN evaluations increase considerably. Figure 6 & 7 Show the numbers changes of the curve number in intensity of 46.7 mm/h on different slopes (4%, 6%, 8%) for various type of soil (A, B, C), based on the results have been excavated from graphs for special type of soil. Equable rainfall intensity, determined that changes in slopes don’t have significant impact on CN evaluations. But at equable slope with increasing the percentage of clay, CN evaluations increase significantly.

Figure 8 & 9 show the curve number evaluations changes on slope of 4% for different intensity (29.5, 35, 46.7) for various kind of soil (A, B, C) at two state (with and without vegetation). According to the results of diagrams in specific rainfall intensity and for stable slope, changes on grading don’t have significant impact on CN evaluations. But at same gradation with increasing at the rainfall intensity, CN evaluations reduced. Figure 10 & 11 express the curve number evaluations changes on slope of 6% for different intensity (29.5, 35, 46.7) for various type of soil (A, B, C) at two state (with and without vegetation). According to the results of diagrams in specific rainfall intensity and for stable slope, changes on grading don’t have significant impact on CN evaluations. But at same gradation with increasing at the rainfall intensity, CN evaluations reduced.

Figure 2 The variation of curve number evaluations base on slope and type of soil at 29.5mm/h stable precipitation without vegetation.

Figure 3 The variation of curve number evaluations base on slope and type of soil at 29.5mm/h stable precipitation with vegetation.

Figure 4 The variation of curve number evaluations base on slope and type of soil at 35 mm/h stable precipitation without vegetation.

Figure 5 The variation of curve number evaluations base on slope and type of soil at 35 mm/h stable precipitation with vegetation.

Figure 6 The variation of curve number evaluations base on slope and type of soil at 46.7 mm/h stable precipitation without vegetation.

Figure 7 The variation of curve number evaluations base on slope and type of soil at 46.7 mm/h stable precipitation with vegetation.

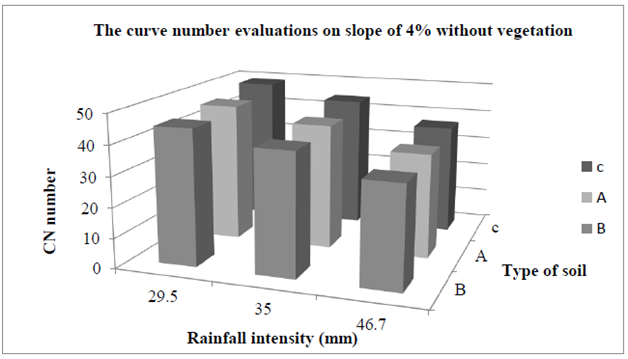
Figure 8 The variation of curve number evaluations base on rainfall intensity and type of soil on stable slope of 4% without vegetation.

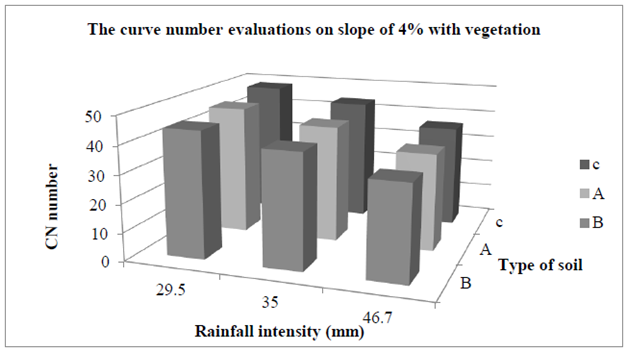
Figure 9 The variation of curve number evaluations base on rainfall intensity and type of soil on stable slope of 4% with vegetation.

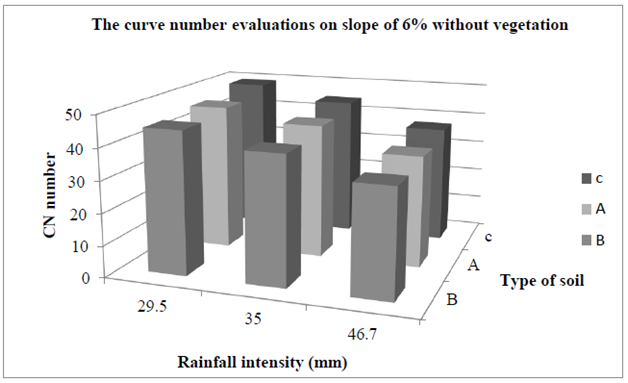
Figure 10 The variation of curve number evaluations base on rainfall intensity and type of soil on stable slope of 6% without vegetation.

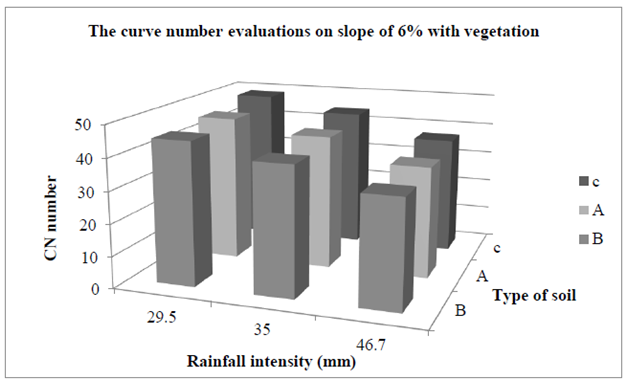
Figure 11 The variation of curve number evaluations base on rainfall intensity and type of soil on stable slope of 6% with vegetation.

Figure 12 & 13 indicate the curve number evaluations changes on slope of 8% for different intensity (29.5, 35, 46.7) for various type of soil (A, B, C) at two state (with and without vegetation). According to the results of diagrams in specific rainfall intensity and for stable slope, changes on grading don’t have significant impact on CN evaluations. But at same gradation with increasing at the rainfall intensity, CN evaluations reduced considerably. According to the achieved results of curve number evaluations in different experiment have been obtained two terms for CN evaluations with and without vegetation.

1)            With vegetation $CN=48/695\ast a^{0/002}\ast b{ }^{0/052}\ast r^{0/728}$

2)            Without vegetation $CN=48/799\ast a^{0/002}\ast b^{0/047}\ast r^1$

The above parameters are:

1. percentage of clay
2. percentage of slope

18. rainfall intensity

Figure 12 The variation of curve number evaluations base on rainfall intensity and type of soil on stable slope of 8% without vegetation.

Figure 13 The variation of curve number evaluations base on rainfall intensity and type of soil on stable slope of 8% with vegetation.

According to results outcomes following conclusions have been achieved:

1. At stable rainfall intensity during the increasing slope, maximum percentage of changes is related to the curve number evaluations and associated with 6% and 8% in state of C type
2. And in the 46.7% rainfall intensity without vegetation that is equivalent of 2.32%. And the lower amount is related to the increasing slope from 4% to 6% in B type soil with 29.5% rainfall intensity with vegetation that is equivalent to 0.36%
3. By evaluating the results of graphs in constant slope of curve number evaluations and comparing the percentage of changes of curve number evaluations, determined in the stable slope that the amount of percentage of changes of curve number evaluations for increasing rainfall intensity from 29.5% to 35% that is equivalent of 10% and for increasing the rainfall intensity from 35% to 46.7% that is equivalent to 20%.
4. With observing the achieved results from collocation of curve number evaluations graphs that supposed type of grading as an effective parameter. The amount percentage of changes for evaluating the changes of grading that is from small gradation (C) to bigger gradation (B) and finally (A). the maximum amount percentage of changes was related to type of grading (C to A) that in 46.7mm/h rainfall intensity for slope of 8% and without vegetation that achieved -6.5% and minimum state was related to the soil gradation from B to A in 29.5% rainfall intensity and 4% slope with vegetation and the amount of -2.4%. that negative mark indicates the reduction of process changes.
5. New formulas have been developed for calculating CN evaluations for both cases of soil with or without vegetation.

None.

The authors declare that there is no conflict of interest.

1. Raj Kaji Shrestha, Mishra SK, Ashish Pandey. Curve number affected by slop of experimental plot having maize crop. Journal of Indian Water Resources Society. 2013;33(2):1‒9.
2. Ebrahimian. Runoff estimation in steep slope watershed with standard and adjusted curve number methods. Environ studs. 2012;1191‒1202.
3. Petroselli. Curve‒Number/Green‒Ampt mixed procedure for net rainfall estimation: a case study of the Mignone watershed, IT. Procedia Environmental Sciences. 2013;113‒121.
4. Van den put. Estimating the parameters of green‒ampt infiltration equation from rainfall simulation data. Journal of hydrology. 2013;232‒244.
5. Mahmood Abadi. Calibration, site distribution and properties of precipitations simulation. Engineering science and Watershed management. 2007;11(1):2007.
6. Rauof. Water and soil knowledge magazine evaluating the influence of slope on amount of infiltration and some of the physical properties of soil. 2011;21(1).
7. Shaikh Rabie. Evaluating amount of the runoff and soil losses in Hio watery basin in scale of precipitation simulation. Earth’s sciences. 2010;26‒75.