International Journal of
eISSN: 2576-4454


Water erosion is the main factor for soil loss in foothills and coastal plain of Oaxaca, with adverse implications for agroecosystems. The objectives of study were to evaluate the soil lost by runoff in a rainy-drought interannual season, in an agroecosystem of Cozoaltepec, Oaxaca and its deposit in the flood plain, through a runoff plot and the Universal Soil Loss Equation. Methodology: Soil samples were collected in thicknesses of 20 cm depth from two edaphic monoliths located upstream-down steam of the study area, By absorption wells the rate of infiltration was estimated, In laboratory, physicochemical analysis were made to determine soil texture by Bouyoucos hydrometer method, pH and electric conductivity (EC) of soil solution by multiparameter tester, cations and major anions by titrimetry, spectrophotometry and flamometry. The soil displaced to the lower parts was calculated through a runoff plot, Collected sediments were averaged and projected to Mg ha-1 and then compared with the values of the equation. Results show that in the experimental plot the erosion was of 4.24 Mg ha-1, while the USLE/RUSLE equation gave 12.32 Mg ha-1. The difference is attributed to the fact that the runoff plot does not consider the factors R (rain erosiveness), K (soil erosiveness), LS (slope length) and P (management practices) consequently erosion is underestimated. By contrast the equation takes them and therefore its results are close to reality. In conclusion the low depth and naked of piedmont soils, as well as the lack of adequate management techniques, cause that these soils are intolerants to hydroerosion.
Keywords: eutric regosol, water erosion, ionic migration, runoff, silt deposit, coastal plain
Since the last century, edaphic disruption by techno genic activities has been constant. The FAO,1 indicates that 33% of the planet’s soils are moderately to highly degraded by erosion, salinization, acidification, compacting and chemical contamination. Water erosion alone, has removed approximately between 25,000 and 40,000 million of Mg from the arable layer of farming soils, which are transported into the oceans.2 This is a limiting factor for production of agricultural crops, given the world food demand. Soil degradation inevitably leads to famine, poverty, migration, and the destruction of ecosystems, mainly in developing countries.3 Forecasts in this matter are hardly encouraging. Should this continue, by the year 2050 an approximate surface of 1.5 million hectares of agricultural lands will be lost. The destruction and loss of soils are a result of population growth, urbanization, and climate change, which act with a negative synergy in food production and the conservation of biodiversity. Water erosion is the removal of soil caused by runoff water, generally from the higher to the lower areas of a basin. Natural erosion occurs with the flow of rivers, streams and runoffs caused by rainfall, which has modelled the reliefs of the Earth’s surface with the passage of geological time. On the other hand, erosion induced by human activity is due to deforestation, the clearing of lands for agriculture, soil compacting, mining, and urban settlements. In all cases the loss of vegetation cover and deforestation leaves the soil naked and at the mercy of hydrodynamic processes which produce the migration of their particles in the runoff water. This removal affects both the areas from which the substrate is removed and those that receive the deposit of sediments.4 More than 75% of the surface of the Mexican territory is vulnerable to water erosion; the uneven relief, the weather, the destruction of vegetation, and the increasing population are all factors that contribute to this. The erosion process progresses faster than the technology necessary to control it. It is estimated an average of 365 million Mg of productive soil are lost every year, out of which 31% remains in the superficial bodies of water, and the remaining 69% is discharged into the ocean.5 In the state of Oaxaca, the erosive phenomenon is explained by deforestation, which affects 30% of the total surfaces of forests and jungles, which have been removed to give way to agricultural and livestock farming activities. The naked surface, steep slopes, and intense rains are factors that induce the removal of a large amount of sediments that migrate from higher lands, and in their descent, deposit sediments in rivers and roads, and cause accidents due to landslides in meso and bas relief areas. In coastal areas, they accumulate or discharge into the ocean.6 The coastal plain of Oaxaca is not exempt to this problem, since it shows signs of erosion, sedimentation, and salinization. For the specific case of the coastal valley near the Cozoaltepec River, there is no knowledge on the scale of the current erosion caused by water, or of the amounts of the sediments deposited in low flatlands. The aim of this investigation was to quantify the mass of soil lost during a rainfall in an agricultural plot in “Barra del Potrero”, Cozoaltepec, Oaxaca, using a runoff plot and its comparison with the universal soil loss equation. This will help evaluate the impact of deforestation on runoff and the amount of sediments removed from the experimental plot to the coastal plain. The results will allow to propose alternatives of sustainable management of the soils to revert the erosive process.
Area of study
It is located in the coordinates 15° 44’ 23.00’’ N and 96° 45’ 40.8’’ W, at an altitude of 59.1 masl. The experimental lands are located six km northeast of the “La Salina” lagoon, and of the town of “Escobilla”, in the property known as “El Potrero” jurisdiction of Santa María Tonameca, Oaxaca (Figure 1). The weather is warm sub humid, with rains of least humid in summer Aw0 (w). The average annual temperature is 27.4°C, dropping to 25.5°C in January the coldest month, and rising to 29.4 °C in May, the hottest month. The average annual variation in temperature is 3.4°C. Total annual rainfall is 1057.8 mm. The driest month is March, with 1.4mm of rainfall, and the most humid month is September, with 255.2 mm.7 The lands are foothills with slopes close to 25%, whose soils are a result of the weathering of metamorphic rocks from the Paleozoic era, which are a part of the Xolapa geological complex.8 Soils are classified as eutric regosols with a sandy loam texture and a massive structure.9 They have a low percentage of clays < 10% and kaolinite is the main mineral colloidal component.7 These soils sustain a deciduous forest vegetation under conditions of intense disturbance due to deforestation caused by changes in soil used to clear lands for agriculture and extensive livestock farming. Downstream, in the coastal plain, there are patches of mangrove and secondary vegetation as a result of human activity.10 The secondary vegetation that grows and develops in the area includes shrubs such as (Calycophyllum candidissium), huizache (Acacia farnesiana), horns (Acacia Cornigera), leadtree (Leucaena leucocephal), manjack (Cordia dentata), bloodwood (Lonchocarpus constrictus), false tamarind (Lysiloma mycrophyllum), beach manzanilla (Crataeva tapia), spoon stick (Cochlospermum vitifolium), cedar (Guazuma ulmifolia) and cocuite (Gliricidia sepium).11 Near of the evaluation site runs the Cozoaltepec river, which drains the western area of the coastal valley of the Tonameca basin (Hydrological region 21 Coast of Oaxaca). The Cozoaltepec river is formed with water from the Sapo river, which is born in San Agustín Loxicha. It presents runoff in the rainy season of 142.90 m3 and a downstream runoff of 142.65m3. Its development is short, and in the rainy season it carries a considerable volume of water.7
Soil sampling and analysis
In the dry season of 2014 (December to May) before the establishment of the runoff plot, a prospective, observational and transversal walking was carried out in the study area. This exploration allowed to distinguish a uniform geomorphology and geochemistry of the landscape.12 On field was determined the infiltration rate (IR) of the soil in cm h-1, using two absorption wells with 0.30 m in diameter and 0.40 m in depth. The first, was established next to the runoff plot, and the second was located in the coastal plain. The infiltration rate was calculated from the surface of soil to the level at which the water column stopped its descent in the hole using the next formula proposed13 , where: (DT)2-(DT)1 is the distance that descends the column of water in the hole in a T2-T1 time period. Later, two soil profiles were established, the first was located upstream, to one side of the runoff plot, while the second was set downstream on the coastal plain at a distance of 300 m. In each profile, samples of soil weighing 2 kg were collected in thicknesses of 0.20m to a depth of 0.80 m. In order to carry out a comparative process and determine differences in edaphic samples in the rainy season (June to November, 2014), soil samples were also taken from two monoliths set up near to those sampled in the dry season. Samples were placed in sealed and labelled plastic bags, and then transported to the area of Soil and Water Analysis of the Seed Laboratory in the Universidad del Mar, where they were dried in the open air. Next, the weights of humid and dry soils were taken using a scale and a muffle furnace at 104 ° C. Then were sifted in 2mm meshes the samples were analyzed to determine their texture and apparent density using the Bouyoucos hydrometer method and the texture triangle.12 The percentage of porous space was calculated using the equation .13 The color of the soil was determined using Münsell color cards.14 For the chemical analyzes the methodology indicated12 was followed. Soil saturation pastes were obtained and tested for pH and electric conductivity (EC) in dS m-1 using a Hanna® model HI98129 multi-parameter tester. Total dissolved solids (TDS in g L-1) were determined using dry calcinated residues (DCR) in a muffle furnace at 600°C. Cations Ca2+, Mg2+ and anions CO3-2, HCO3-1 and Cl-1 were calculated by titration; SO4- 2 by turbidimetry (Perking Elmer spectophotometer), and Na+ and K+ by flamometry (Flamometer IL-653).
Establishing the runoff plot
In selecting the site to establish the runoff plot, the analysis of the phenosystem was considered. This helped locate the place with the ideal characteristics to measure the erosive effect of the runoff, that is, naked soil prepared for the cultivation of peanuts (Arachis hipogea L.), with a steep slope and a trough towards the coast. Thematic maps of soil, vegetation and hydrology of the study area,7 served as support in detecting changes in vegetation and nearby rivers. This site was located on the foot of the southeast end of the agricultural field chosen for evaluation. The slope of the land was calculated as a percentage using a Suunto Tandem/360 PC/360RG clinometer. The measurements of the runoff plot were 2.5m wide by 5m long, which formed a surface of 12.5m2, in which surface runoff and erosion were measured. The plot was established in a north-south direction (upstream-downstrwam from the microbasin) and fenced with wood boards, 5m long by 0.25m high, buried at a depth of 0.1 m. The southern end of the structure was connected in its lower part to a PVC tube, 1 m long and 4 inches in diameter, which was used to conduct water with sediments to a plastic container with a capacity of 100L, as indicated in Figure 2. The container was placed under the end of the tube and buried at a depth of 0.20m below the ground’s surface to collect the sediments removed during the erosive process. Later, the gathered sediments were dried in the open air and weighed using a scale balance of 100kg. The sediments collected each month were summed to obtain the total sedimentary externalities in the interannual periods evaluated. The samples were then transferred to the laboratory to determine their actual dry weight by muffle at 104 °C. The amount of sediment eroded was projected to Mg ha-1. Then sediment samples were analyzed to determine their physico- chemical properties by the methods listed above.
Calculation of actual and potential erosion using the universal soil loss equation
In order to compare the results of the soil erosion obtained from the runoff plot, the actual and potential erosions in the area studied were calculated using the Universal Soil Loss Equation proposed by Wischmeier and Smith,15 indicated below:
(1)
Where:
A, Soil loss by surface unit (Mg ha-1);
R, Rain erosive factor; This is the accumulated product of the kinetic energy times the maximum intensity of the rain in 30 minutes for a period of interest (generally one year in agroecosystems), with an average probability of occurrences of 50%. Its units are MJ mm/h/year. In this respect, Clérisi and García,16 consider that for purposes of simplicity, R can be evaluated in units of energy per surface (J ha-1).
K, Soil erodability factor; This is the average amount of soil lost per unit of factor R (Mg ha-1), in soil that remains naked, with secondary tilling in the direction of the slope.
L, Length of slope factor; This is the ratio between the erosion with a given slope length and that which takes place in a standard length of 22.1 m, while the other factors remain constant.
S, Steepness of slope factor; This is the ratio of the erosion with a determined inclination of the slope, and that which takes place on a piece of land with a standard slope of 9%, while the other factors remain constant.
C, Use and management factor; This is the ratio between soil erosion with a particular use and management system, and that which takes place in the same land in the standard conditions in which the K factor is defined, in equal conditions to the other factors.
P, Support in mechanical practices factor; This is the ratio between the erosion produced by a particular type of mechanical practice and that produced in standard tilling conditions in the direction of the slope. The other factors remain constant. The reference equation was modified for the conditions of Mexican soils by Colegio de Postgraduados-SARH,17 based on numerical erodability curves that estimate factor C, using five easily determined variables:
Determination of the rainfall erosion index
The potential capacity of the rains to induce erosion in the soils of the area under study was calculated as the average intensity of the rainfall (amount of rain in mm that falls in an hour), and for this we used rainfall data of Cozoaltepec, Oaxaca weather station. To work out the kinetic energy (KE) of the rain, was used Hudson´s equation, utilized for tropical rainfall areas in India by Yusof et al.,18 which is indicated below:
(2)
Where:
KE, Kinetic energy J m-2 mm-1;
I, Intensity of the rainfall (mm h-1)
Calculation of the potential erosion (PE)
In this calculation, the factors RKLS of the Universal Soil Loss Equation were taken into account, as well as formulas to obtain each factor as follows:
Erosive factor (R)
In this case, we gathered the averages of monthly and annual rainfalls throughout 30 years of the geographic summer for the coast of Oaxaca,19 which served to feed the equation of Lombardi and Moldenhauer:20
(3)
Where:
R, Erosive index of the average annual rainfall (Mg ha-1);
P, Average monthly rainfall;
P, Average annual rainfall;
Coefficient used to determine R in tropical areas.
Soil erodability factor (K)
The susceptibility of the soil to the erosive action of water depends on the physical properties of the soil, such as texture, structure, porous space, permeability, hydraulic conductivity, infiltration, organic matter content, etc. These aspects are taken into account in the equation of Wischmeier and Smith,15 modified for metric units by Irurtia and Cruzate cited,21 as follows:
(4)
Where:
% of silt, Percentage of the mineral fraction from 2 to 50 µ in diameter;
% of sand, Percentage of the mineral fraction from 50 a 100 µ in diameter;
% of clay, Percentage of the mineral fraction < 2 µ in diameter;
OM, Percentage of organic matter in the superficial layer of the soil;
b, Degree of aggregation of the soil according to the following scale:
c, Permeability of soil according to the following scale:
Length of slope factor (LS)
For its calculation we used the equation by Wischmeier and Smith,15 modified by FAO,22 which considers slope length data (L) in m and of the slope (P) as a percentage, as follows:
(5)
Where:
L, Length of slope (m);
P, Land steepness in %;
m, Exponent that varies with the slope as indicated as follows: For lands with a slope of up to 0.5%, m = 0.2. For slopes between 1 and 3%, m = 0.3. For slopes between 4 and 5%, m = 0.4. For slopes > 5%, m = 0.5.
Determination of actual erosion (AE)
Calculated with the values of the potential erosion (PE) values and the factors C (soil use and management) and P (soil management or conservation practices). To determine the value of factor C, were considered the indices established by the Soil and Water Conservation Manual,17 presented in Table 1. On the other hand, the value of P was obtained considering the options of possible conservation practice in the area of study, proposed in the aforementioned Soil and Water Conservation Manual, which are indicated in Table 2. Using these elements, the equation 1 expressed as AE = (PE) (C) (P), was fed and the current erosion was obtained.
Estimation of the surface runoff
To relate the intensity of the erosion process with the volume of water runoff in the area of study, the surface runoff was calculated using the equation proposed by Pilgrim et al. 23
(6)
Where:
Q, Surface runoff m3 s-1;
C, Runoff coefficient;
I, Intensity of rain mm h-1;
A, Microbasin area;
3.6, Factor of conversion from hours to seconds.
The maximum rain intensity was obtained based on the data of the rainiest days of the year for an average of 30 years for the region, obtained with the time and space characterization of the monthly rainfall and humidity available in the state of Oaxaca,19 which gave 280 mm as the highest daily rainfall. To this effect, the equation indicated by Salas et al.24 was used:
(7)
Where:
Id, Daily maximum rainfall intensity (mm)
Afterwards, was calculated the average maximum rain intensity for one hour, which made it possible to calculate the maximum rainfall intensity for any interval of time (t), using the equation proposed by Salas et al.24
(8)
Where:
It = Rainfall intensity for any interval of time.
Id = Maximum daily rainfall intensity.
I1 = Intensity in the rainiest time.
t = Time of concentration.
Calculation of the time of concentration (t)
The time of concentration is the time passed between the fall of one raindrop on the highest point of the microbasin studied and its migration in the river bed up to the section or point where the runoff produced is to be quantified.25. For its calculation we used the equation proposed by Pilgrim et al.23
(9)
Where:
Tc = Time of concentration (h).
L = Length of river bed
J = Average slope, calculated using the following equation:
(10)
With these elements it was possible to use equation 8 to obtain the intensity for any interval of time.
Calculation of the runoff coefficient (C)
Coefficient C expresses the ratio between the volume of water that flows through a section of the basin due to rain, and the volume of rain water. To calculate this, the formula suggested by the Department of Soil Studies of the United States Department of Agriculture,26 was used and is indicated below:
(11)
Where:
Pd = Maximum daily rainfall.
P0 = Rainfall threshold.
After obtaining the data of the variables designed, the volume of runoff was calculated using equation 6.
Estimation of the gross erosion and that which could migrate downstream in the management conditions of the property known as “El Potrero”
To determine the percentage of sedimentary externalities of the land studied, as well as its contribution to the amount of sediments deposited in one year in the low plains; the surface of the experimental field (two hectares), the type of use of the soil of the plot classified into percentage of natural area (Cn = 10%), area planted (Ac = 60%) and grassland area (Pa =30%), as well as the sediment transportation coefficient of runoff (C= 0.79), the apparent density of the soil (1.46 g cm-3) and the depth of the arable layer (0.10 m), were considered. With the partial gross erosion of each soil use, multiplied by the sediment transportation coefficient, it was possible to determine the partial mass of soil that migrates and is deposited downstream according to each area with a specific use and the total gross erosion.27 Finally, to quantify the accumulation of sediments deposited downstream site during the rainy season, eight PVC soil collectors of four inches in diameter and 50 cm in length were installed at random in lands of the plain adjacent to the property, covering an area of 45 x 103 m2 (approximately 180 m wide of the Cozoaltepec river valley, for a longitudinal section of 250 m of shoreline).The sites were marked on a Garmin (76S) GPS, and the amount of sediments collected was averaged and projected to units of Mg ha-1. With the difference of the total gross erosion - the mass of sediments accumulated in PVC tubes and projected to surface units, was estimated the amount of sediments deposited in the low plain.
Plant coverage |
C |
Forest without intervention |
0.001 |
Forest with intervention |
0.34 |
Lands eroded with scarce vegetation |
0.8 |
Naked soil |
1.0 |
Extensive crops in rows |
0.5 |
Manioc and sweet potato (first year) |
0.2-0.8 |
Palm, coffee, cocoa |
0.1-0.3 |
Grasslands |
0.07 |
Vegetables |
0.3 |
Table 1 Index values of the soil use and management factor
Source: soil and water Conservation Manual by Colegio de Postgraduados-SARH.17
Technique |
Factor P |
Level curves (5-20% slope) |
0.1-0.7 |
Anti erosion bands, from 2 to 4m (5-25%) |
0.1-0.3 |
Protection with hay |
0.01 |
Terraces of 80cm, combined with level curves (15 to 30% slope) |
0.1 |
Table 2 Conservationist practices index
Source: Soil and Water Conservation Manual by Colegio de Postgraduados-SARH.17
Physical and chemical characterization of the soils upstream and downstream from the microbasin
The vertical anisotropic analysis of the soil monolith No. 1, located in the limits of the foothills with the coastal alluvium, indicates a poor development of its horizons A and B. These have been formed by the weathering of metamorphic rock (gneiss granite) of the Paleozoic, which even appear on the surface, and by the light deposit of sediments carried by the runoff water.8 Horizon A varies in thickness, from 1cm to 4 cm, and it accumulates plant residues which decompose rapidly due to high temperatures and humidity. Horizon B reaches depths of up to 1.5m and presents processes of eluviation and illuviation in which kaolinites and iron and aluminum hydroxides are displaced and accumulated. These soils are not deep and their lithic phase produces a slow natural drainage and low permeability. Also it has a low rate of infiltration whose calculation using an infiltration well, was of 4.5cmh-1. This condition, along with the slope with a steepness of 25% has an influence such that surface runoff is a recurring phenomenon. This description coincides with,28 for soils of the mesorelief of San Pedro Mixtepec. The edaphic texture was determined to be sandy loam, with a density of 1.46 g cm-3 and 45% of porous space. The amount of organic matter varies between 3 and 1% as one descends in the profile. Soil color is reddish-brown (7.5 YR 4/2) and indicates the presence of iron minerals in a state of oxidation, such as hematite (Fe2O3), common to tropical soils with forest vegetation. On the other hand, the edaphic monolith No. 2 corresponds to soils formed by unconsolidated soils, created by the weathering of metamorphic rocks of the Sierra Madre del Sur. The sediments migrate and accumulate in the coastal alluvial plain. These soils present well developed horizons. Horizon A is approximately 20 cm thick, and shows subhorizons Oa, composed of fresh matter in decomposition, and Oi, in transition between organic and mineral matter. Horizon B can reach up to 2 m in depth, and processes of eluviation and illuviation of iron and aluminum sesquioxides take place in it. The texture of these soils is sandy loam and the apparent density is 1.47 g cm-3. The greatest presence of silty and clay particles obstruct the porous system of the soil, which is reduced to 40%. This physical condition, related to the light steepness of 2% of the coastal valley, produces a deficient natural drainage, which explains the IR value obtained by a soak away of 2.4 cm h-1. These values coincide with those reported3 for coastal soils of Oaxaca. Soil color is dark brown (7.5 YR 3/3), indicating the accumulation of silts transported by alluvion, and organic matter provided by agricultural amendments, with values ranging between 4 to 5%. Table 3 and Table 4 shows that both soils before and after the hydroerosion process, have a slightly acidic pH (~6.7) and a low EC of the soil solution with an average value of 0.53 dSm-1 for foothill soils, and 1.73 dS m-1 for lower flood plain soils which show no salinity problems. Figure 3 and Figure 4 shows the ionic concentrations obtained from aqueous extracts of saturation pastes from both soils before and after the erosive process. A low concentration can be observed in foothill soils. In their solution there is a predominance of Ca2+ and the anion HCO3- which form calcium bicarbonate salt, common in regosols formed from a metamorphic limestone rock (Figure 3). The ionic concentration increases slightly in the soils in plains (Figure 4), since the solution of the upper thickness presents a predominance of Na+ ions over Ca2+ and Mg2+, and of Cl- over HCO3- and SO4-2.
Estimation of potential and actual erosion using the Universal Soil Loss Equation
Obtaining the potential erosion with the Universal Soil Loss Equation (15), required, firstly, calculating the energy coefficient (KE) of the rain in the area under study. For this, we considered the daily average maximum rainfall in 30 minutes (I30) between June and November, 2014 for the area of Cozoaltepec, Oaxaca, which was 51.88 mm h-1.21 When this value was introduced into equation 2, we obtained a KE of:
> (12)
On the other hand, the calculation of factors R, K, and LS, needed to obtain the PE, gave the following results:
In determining factor R, the average data for monthly (p=82.06 mm) and annual rainfalls (P = 984.8 mm) reported for the area of Cozoaltepec in a thirty-year period were considered.19 These were placed in the equation by Lombardi Neto and Moldenhauer,20 producing the following result:
(13)
The calculation of factor K based on equation 4, considered the following physical aspects of the soil: textural condition determined as loamy sandy, with a low percentage of colloidal material. Its regular structure with a low content of organic matter, the poor drainage and the moderate infiltration rate of 4.5 cmh-1, which, according to,28 present higher runoff values. With this equation modified by Irurtia and Cruzate and cited,21 we obtained the following value:
(14)
The determination of the LS factors were supported with the topographical work carried out in the runoff plot, which gave a length of 12 m and a slope of 25% steepness. When substituting these values in equation 5, the following value was obtained:
(15)
Using these results, we calculated the PE, estimated with the multiplication of these factors, as indicated below:
PE=R∙K∙LS
Thus, PE = (35.2) (0.16) (3.90) = 22 Mg ha-1 per year.
To calculate AE, not only the aforementioned factors were considered, but also the C and P factors, the indices of which were chosen according to the values proposed by the Soil and Water Conservation Manual17 in Table 1 and Table 2, which were associates according to the soil and conservationist use and management practices carried out in the property known as “El Potrero”. In this way, the value of factor C is of 0.8 since they are eroded lands with scarce vegetation; whereas the value of P was obtained considering that the appropriate conservationist practice for the experimental field are the level curves, hence the value assigned of 0.7. Therefore, based on equation 1, when substituting the corresponding values, AE gave the following result:
(16)
Estimation of erosion by the runoff plot
The mass of soil removed in the runoff plot during the rainy season was 5.30 Kg in a surface of 12.5 m2. Its projection to surface units (ha) gave as a result the amount of 4.24 Mg ha-1/ year of sedimentary externalities produced by water erosion.
Evaluation of surface runoff
The evaluation of surface runoff used equation 6 by Pilgrim et al.23 and for this, the maximum rain intensity (I) was obtained. This factor was determined with the maximum daily intensity (Id) data for the rainiest days for a thirty year period in the area.19 The average of this value was 300 mm, which, divided by 24 hours, gave an (Id) of:
(17)
Next, the maximum rain intensity was calculated for any given time interval t (It). For this, the maximum daily rainfall value was considered, and using regression analysis, was projected the average maximum rain intensity for one day (I1), which gave a value of 100 mm h-1. This data was entered into equation 8 proposed by Salas et al.24 indicated below:
(18)
The resolution of this equality required to know the time of concentration (Tc), obtained from equation 9 proposed by Pilgrim et al.23 as well as consider the length of 14 Km of the Cozoaltepec river bed, gave the following result:
(19)
These elements helped calculate equation 8, as follows:
(20)
Therefore
On the other hand, for the calculation of the coefficient of runoff C, we used equation 11.26 This case considered the average value of maximum daily rainfall for the area of 300 mm and the rainfall threshold of 19 mm. When substituting the data in the equation, the result was as follows:
(21)
The value of C obtained, falls in the interval of trust of runoff coefficients proposed by the United States Soil Conservation Service.22 Finally, the volume of runoff was obtained using equation 6, and gave a value of:
(22)
Estimation of the gross erosion and that which migrates downstream in the management conditions of the area under study.
Gross erosion gave a total value of 2360 Mg ha-1/ year, out of which 1864.4 Mg ha-1/ year migrate and are deposited in the lower flood plain of the study area or are transported into the ocean (Table 5). The estimation procedure indicated in the Methodology chapter has been satisfactory for computing gross erosion in the basins of the main rivers in Argentina and Uruguay.16,27
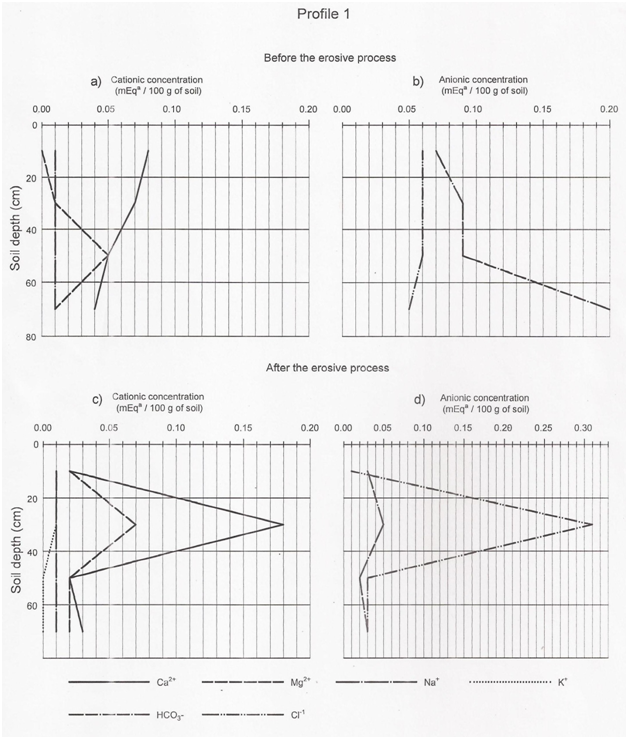
Figure 3 Distribution and ionic concentration in thicknesses of soil profile 1: a. Cations and b. Aniones, before hydroerosion, c. cations and d. anions, after hydroerosion.

Figure 4 Distribution and ionic concentration in thicknesses of soil profile 2: a. Cations and b. Aniones, before hydroerosion, c. cations and d. anions, after hydroerosion.
No. Profile |
Soil thickness (cm) |
pH |
EC(a) (dS m-1) |
TDSb (mg L-1) |
Statistical parameters |
|
EC (dS m-1) |
TSD (mg L-1) |
|||||
1 (Foothill) |
0-20 |
6.49 |
0.39 |
247.94 |
M = 0.31 |
M=199.52 |
20-40 |
6.73 |
0.31 |
196.03 |
σ = 0.06 |
σ =35.48 |
|
40-60 |
6.62 |
0.32 |
205.95 |
CV = 0.19 |
CV= 0.17 |
|
60-80 |
6.53 |
0.23 |
148.16 |
|||
2 (Coastal plain) |
0-20 |
6.93 |
1.16 |
741.76 |
M =1.71 |
M= 1,095.20 |
20-40 |
6.73 |
2.27 |
1451.52 |
σ = 0.45 |
σ= 290.63 |
|
40-60 |
6.71 |
1.79 |
1144.32 |
CV= 0.26 |
CV= 0.26 |
|
|
60-80 |
6.72 |
1.63 |
1043.2 |
|
|
Table 3 Values of pH, EC and TSD of soil profiles analyzed before the hydroerosive process)
pH, hydrogen potential; (a)EC, Electric Conductivity; (b)TDS, Total Dissolved Solids. M, mean; σ, standard deviation, CV, coefficient of variation.
No. |
Soil thickness |
EC(a) |
TDS(b) |
Statistical parameters |
||
Profile |
(cm) |
pH§ |
(dS m-1) |
(mg L-1) |
CE (dS m-1) |
STD (mg L-1) |
1 |
0-20 |
6.49 |
0.18 |
117.25 |
M = 0.54 |
M=346.11 |
(foothill) |
20-40 |
6.73 |
0.6 |
385.28 |
σ = 0.45 |
σ =290.72 |
40-60 |
6.62 |
0.12 |
76.16 |
CV = 0.84 |
CV= 0.84 |
|
60-80 |
6.53 |
1.26 |
805.76 |
|||
2 (Coastal plain) |
0-20 |
6.93 |
0.29 |
185.15 |
M =0.25 |
M= 179.22 |
20-40 |
6.73 |
0.12 |
76.22 |
σ= 0.10 |
σ = 71.58 |
|
40-60 |
6.71 |
0.36 |
230.53 |
CV= 0.40 |
CV= 0.39 |
|
|
60-80 |
6.7 |
0.25 |
225 |
|
|
Table 4 Values of pH, EC and TDS of the soil profiles analyzed after the erosion process
§pH, hydrogen potential; (a) EC, Electric Conductivity; (b) TDS, Total Dissolved Solids; M, mean; σ, standard deviation; CV, coefficient of variation
Soil use |
Gross erosion (Mg/year) |
Migration and deposition of sediments (Mg/year) |
Proportion of erosion in the lower flood plain. |
NF |
236 |
186.44 |
0.1 |
Gr |
708 |
559.32 |
0.3 |
Ag |
1,416 |
1,118.64 |
0.6 |
Total |
2,360 |
1,864.40 |
1 |
Table 5 Estimation of the gross erosion and that which could migrate downstream in the management conditions of the property “El Potrero”
NF, Natural fields; Gr, Grasslands; Ag, Agriculture
According to the indicated physicochemical properties and the soil classification by FAO,9 the piedmont soils of Monolith No. 1 are eutric regosols, while the coastal soils of monolith No. 2 are eutric cambisols. Both have a slightly acidic pH and a low EC that distinguishes them as soils without salt problems (2013). The pH is related to the presence of iron and oxidized aluminum. While EC values have an explanation in the poor content of basic cations (Ca2+, Mg2+, Na+ and K+) which are lixiviated in the rainy season, migrate in the drainage water and accumulate in the soils of the lower parts.28 Both present a fragile balance with the vegetation due to the intense perturbation they have been placed under. The low ionic concentration determined in the piedmont soil thickness, and its increase in the upper thicknesses of the surrounding coastal plain soils, with a predominance of Na+ over Ca2+ and Mg2+, and of Cl- over HCO3- and SO4-2 is explained in the migration processes of elements during the hydroerosion and where the geochemistry of the elements indicates that the more mobile ones like Na+ and Cl-, migrate faster than cations such as Ca2+ and Mg2+ and anions such as HCO3- and SO4-2, due to their ionic energy coefficient, ionic radius, hydration radius and their valence.28 The foregoing is consistent with the point made by Kokof 2 who affirms that this ionic accumulation is related to the accretion of sediments in the coastal plain, but also with the geochemistry of these elements and the speed at which they migrate in runoff waters.29 This ionic and EC variation in the toposequence clearly shows a process of ionic migration from the meso relief and its accumulation in the low relief derived from sedimentary particles eroded. The phenomenon observed is important for foothill soils, which lose fertility, and for coastal alluvial soils, which gain fertility. However, in time, this ionic accumulation, along with weather conditions of excess evaporation, scarce rainfall and a rise of the water table near the surface, characteristics of the area studied, produce a tendency to accumulate salts in the upper layer of the soil, which coincides with what was indicated out.30
Regarding the values obtained for the different factors of potential erosion of soils through the respective equations, all indicate a tendency of the soils under study to be eroded by the runoff water.31 For example the value of KE = 27.33 J m-2 means that the rainfall intensity estimated for the study area has a high erosive potential. For its part, the calculation of the R factor that considered the physical properties of the soils under study yielded 35.2 Mg ha-1 of erosive capacity, it represents high values of surface runoff.28 In addition to the above, the value of the factor K = 0.16, is in the range of values (0.13-0.38) established by the Soil Conservation Service of the United States of America for a B type soil, with the physical properties mentioned above, which indicates the correct determination of factor K.32 For its part, the LS topographic factor was 3.6, so the potential erosion was 22 Mg ha-1. According to the classification of potential erosion carried out,15 the studied soils are affected by a slight potential erosion. Also when considering factor C with a value of 0.8 because it is an eroded soil with little vegetation cover and a value of 0.7 for the P factor, corresponding to a management practice with contour lines and row crops,17 it was obtained an AE of 12.32 Mg / ha / year, this value indicates that the eutric regosols of the foothill analyzed are very vulnerable to water erosion, since its scarce depth and moderate structural condition makes them little tolerant to the erosive process. This coincides with,16 who claim that naked and shallow soils are susceptible to losing a large amount of sediments during an erosive process. On the other hand, the erosion obtained by the runoff plot was 4.24 Mg / ha / year. This value is lower than that obtained using the Universal Soil Loss Equation (12.32 Mg ha-1/year). The difference is of 8.08 Mg ha-1/year. Similar data were obtained28 in eroded soils in the microbasin in San Pedro Mixtepec, Oaxaca, where the runoff plot gave 9.2 Mg ha-1/year. However, the Universal Soil Loss Equation estimated an erosion of 16.67 Mg ha-1/year. For researchers such as18 this difference is due to the empirical simplicity of the calculation of erosion in a runoff plot which neglects aspects as important as the coefficient of potential erosion caused by rains, the soil erodability or its use, management, and conservation. Therefore, this method to determine erosion sub evaluates actual erosion. For its part, the use of the USLE/RUSLE equation gives erosion values with a greater similarity to what takes place in the soil, since it predicts the effect of the erosive potential of rain in a particular region, considering the factors of texture, slope, plant coverage, and the type of management and conservation, as indicated.16 However, the runoff plot method is considered useful to obtain an overall idea of the degree of erosion in a particular soil, since, despite its giving a lower amount of sediments removed from a particular area, the value of 4.24 Mg ha-1 / year is higher to the threshold of tolerance to erosion for this type of soils.22
The data in Table 5 indicates an accumulation of sediments higher than that obtained by the evaluation of the mass of soil collected in the PVC containers placed in the low flood plain, since the projection per hectare of the collected sediments threw a sedimentary deposit of 6300 Mg /year for a surface of 45 x 103 m2, that is 1006.41 Mg ha-1/year. These values are enormous, considering that the evaluated section of the coastal valley of the Cozoaltepec river was of 180 m wide, for 250 m of coastline with a depth of 0.10 m of soil and a density of 1.46 g cm-3. Everything seems to indicate that the difference between the theoretical sedimentary deposit (1864.4 Mg ha-1/ year) and that obtained in the field (1006.41 Mg ha-1/year), that is, approximately 800 Mg ha-1/year of sediments were transported into the ocean. The values of gross erosion are widely linked to the ionic migration induced by surface runoff, since it implies the loss of fertility of the soil in the area where the sedimentary externalities take place. This is a reason to point out that the productive systems practiced in the area have a high degrading impact in the soil and hence are unsustainable. Consequently, it is necessary that farmers of the region carry out erosion control techniques, such as the establishment of contour ploughing, row crops, soil coverage with harvest residues, terracing, border canal systems, drainage canals, windbreaker barriers, and hedgerows, in order to control the erosion and transportation of sediments towards the beds of rivers and streams that drain the lower parts of the microbasin. Likewise, it is also necessary to implement agroforestry systems in terraces.33‒36 About works in grasslands with slopes of 30% steepness in the neighboring region of San Pedro Mixtepec, Oaxaca, where settled terraces cultivated with Moringa oleifera L. and Leucena leucocephala L., indicates an erosion reduction of 87%, originally calculated in 16 Mg ha-1/year.28 That shows the effectiveness of this erosive control system. It is also necessary for agricultural and forestry extensionism to become more active in the region, so as to promote the planting of legumes as a protection for the arable layer. As an alternative, the planting of Canavalia (Canavalia ensiformis L.) in association with traditional maize crops, has proven to provide mechanical stability to the edaphic particles, and the contribution to the soil with up to 231 kg ha-1 of nitrogen.35 Likewise, it is necessary to consider the timber-yielding crops-species based on which farmers may have the option of conserving the soil as a productive agricultural asset and obtaining a long-term incomes from wood production and sales. For the area under study, a feasible option can be the planting of Acacia mangium Willd and Acacia auriculiforme Benth, which have been used successfully in some parts of the Mexican southeast to stabilize eroded hillsides and improve soil fertility.36 Finally, the loss of waterfront vegetation in the lower part of the Cozoaltepec river, adjacent to the land under study, and the excessive deposition on eroded sediments causes the sedimentation of its bed, the instability of its banks, a change in the chemical quality of the waters, the loss of water which is shorter in the dry season, and the formation of arid sedimentary banks. For this reason we propose the reforestation in the high and mesorelief, as well as the repopulation of the creek with trees such as the amate (Ficus cotinifolia Kunth), the Jamaican nettle tree (Trema micrantha L.) and the tololote (Andira enermis Kunth), which can be planted along with strips of grass to increase the retention of sediments and mitigate its migration towards the ocean.
Estimation of soil erosion through the runoff plot underestimates the AE obtained with the Universal Equation of Soil Loss, at approximately 8.08 Mg ha-1/year. This is due to the empirical simplicity of calculating erosion in a runoff plot, which does not consider such important factors as the potential erosion coefficient caused by rainfall, soil physical properties, topography and type of use, management and soil conservation. The magnitude of the erosion obtained by the equation, together with the volume of runoff of indicate intense effects of soil degradation by water erosion. The PE and the AE are values that in regosols of the area under study, indicate intolerance to water erosion. The productive system practiced (agriculture in furrows, with a steepness close of 25%, without coverage and level curves) is unsustainable, given the sedimentary externalities which impoverish piedmont soil.
The authors acknowledge the support provided by Universidad del Mar and Colegio de Postgraduados for conducting this research.
Author declares there is no conflict of interest

© . This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.