Recently, the enormous features have been utilized to increase the heat transport behaviours like changing geometry of flow and enhancing their thermal conductivity. Increasing challenges of more proficient heat transport liquid, there is require creating a new sort of fluid that are more influence in the form of heat transport phenomenon. The addition of nanoparticle in the ordinary fluid is one of the new science methods to boost heat transport increment. Most of the ordinary fluid like water, ethylene, glycol mixture have less heat transport rate. To enhance thermal conductivity with heat transport rate and it is essential to exploit the nanoparticles in the ordinary fluid. To envisage behaviour of nanoliquid several models have been presented in the literature. The novel idea was introduced Choi.1 Later, the Buongiorno2 has been attracted noteworthy attention owing to reasonable explanation of nanoparticles mechanism. Makinde and Aziz3 numerically explored the viscous boundary layer nanoliquid near convective surface. Pal and Mondal4 studied the MHD flow of non-isothermal nanofluid with convective condition near stagnation point. Turkyilmazoglu5 reported an influence of the viscous fluid on the hydromagnetic nanoliquid flow of a heat and mass transmit due to a slip conditions. The generation/absorption on three dimensional Oldroyd-B nanoliquid near stretching surface with an effect of heat has considered by Khan et al.6 In addition, Sisko nanoliquids past stretching sheet with the effect of heat transfer are presented via Khan et al.7 The two constrain boundary conditions of nanoliquid due to a vertical surface has been deliberated by Kuznetsou and Nield.8 Hayat et al.9 developed the mixed convective flow visco-elastic nanofluids through a cylinder with heat source/sink. The MHD flow of nanomaterial with convective conditions has been created by Hayat et al.10 A significant of nonlinear mechanics and utilising the effect of thermophoretic and Brownian movement are explained by Khan et al.11,12
The megnetohydrodynamic (MHD) are used in different areas of science and technology like molten metal and pumping station. The thermal stratification transient-free convective flows for nano liquid are investigated by Peddisetty.13 The effect of heat sink-source with Burgers flow model under nanomaterial the due to stretched sheet considered by Khan and Khan.14 The features of nanofluids for boosting the effectiveness of solar collectors are examined by Sheikh et al.15 Khan et al.16 conducted the effect of solar energy of MHD of Carreau nanofluid using the features of solar energy.
Now days, the demanding of the non-Newtonian fluids have been studied widely owing their significant applications in engineering, medicine and industries. There is non-linear correlation between shear stress and strain in this type of fluids. The study of non-Newtonian flow and the heat transport phenomena having shear effect. Cream, catch up and polymer solution are the few example of hyperbolic tangent fluid. This fluid model has sure benefit due to other than non-Newtonian fluid containing model formulation, simplicity of calculation and physical strength. Moreover, this flow model explains the blood flow very precisely.17,18 Hayat et al.19 examined MHD tangent hyperbolic nanoparticles over variable stretching surface. The EMHD unsteady hyperbolic tangent nano liquid with convective boundary condition has been observed by Mahdy and Hoshoudy.20 Salahuddin et al.21 noticed stagnation point and hyperbolic tangent nanomaterial due to a stretching cylinder. The numerically study of hyperbolic tangent nano liquid over sphere was considered by Gaffar et al.22 The tangent hyperbolic due to stretching sheet and partial slip condition is ascertained by Ibrahim.23 The influence of dual stratified on MHD tangent hyperbolic nano liquid due to permeable cylinder was conducted by Nagendramma et al.24 Recently, Kumar et al.25 examined three dimensional tangent hyperbolic fluid over bidirectional flow at convective boundary condition. More recently, Ramzan et al.26 analysed the activation energy and Hall effect in a partially ionized tangent hyperbolic nano liquid under Cattaneo-Christive. The investigation shows that flows with nonlinear thermal radiation have not given much attention of many researchers because of wide ranging application. Such application contains design of furnace, gas turbines, glass production, nuclear plants, and space technologies. Cortell27 presented nonlinear thermal radiative heat transfer near stretching sheet. The three-dimensional Jeffrey nanofluid flow under nonlinear thermal radiation is investigated by Shehzad et al.28 Pantokratoras and Fang29 described Sakiadis flow and nonlinear Rosseland thermal radiative. Animasaun et al.30 reported homogeneous/heterogeneous reactions within visco-elastic fluid flow under magnetic-field and nonlinear thermal radiative. MHD three-dimensional flow of nano liquid with velocity slip and nonlinear thermal radiative is explored by Hayat et al.31 The 3D MHD nano liquid past shirking sheet with the combined result of thermal radiative with viscous dissipation are scrutinised by Nayak.32 Ramzan et al.33 explained 3D visco-elastic nano liquid with thermal radiative and mixed convection.
The aim of current of investigation is to communicate the 3-D flow MHD tangent hyperbolic nanofluid towards a stagnation point with heated convective condition. Study has been obtained under thermal radiation with chemical reaction, Soret and Dufour effects. Set systems of governing PDE’s are reduced to the set of ODE using appropriate transformation. The set of ODE’s are utilized through Bvp4C along shooting technique. Sketch for velocity, temperature and concentration as well as skin fraction, heat and mass have been displayed graphically and tabular form.
The Cauchy stress tensor is
(1)
where
is stated as
(2)
Then tensor Eq. (1) become as
(3)
Mathematical formulation
We ponder the unsteady 3D tangent hyperbolic nanofluid near stagnation point. The flow is persuaded along XY-plane (Z=0) through bidirectional stretched with streching velocities
,
,
along XY-direction, where a, b and c are constant. The flow occupied the region Z > 0. Seen in Figure 1 the geometrical representation of current investigation. A non-uniform magnetic field
is computed. Where B0 is magnetic field strength.
(4)
(5)
(6)
(7)
(8)
(9)
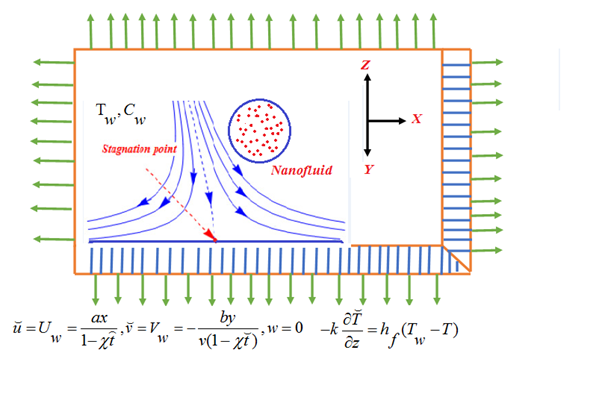
Figure 1 Model of the flow.
Considering the transformation
(10)
(11)
(12)
(13)
(14)
With boundary conditions
(15)
The physical variables in the above expressions have been declared as follows
(Weissenberg number)
(Unsteadiness Parameters)
(Dufour)
(Soret)
(Eckert number)
(Radiation variable)
(Brownian motion)
(Thermophoresis)
(Magnetic Parameter)
(Prandtl number)
(Scimdth number)
The physical quantities
(16)
Where
and
are the shear stress along
and
directions, respectively,
is heat flux, and
is the mass flux.
Using similarity variables, we obtain
(17)
Where
Implemented Strategy
The highly nonlinear ODE’s Eqs. (11) - (14) associated to boundary condition Eq. (15) are transmuted into first order with along Bvp4C-technique for diverse values of emerging parameters. For the purpose, we choose new variables.
The above defined set of first ODE’s is utilized via Runge-Kutta method by assigning few missing variables l, m, n and o. The step has measured as
. The process is frequent until criterion is not converge of
.
Code validation
To verify the precision of current calculated outcomes with previous available data, a evaluation has made between latest computed outcomes and existing literature in limiting case. Table 1 exhibits a comparing of the numeric outcomes for the skin fraction for the various estimation offor various estimation of the unsteady
variable when We = n = 0, published outcomes of Ali and Zaib35 and Khan et al.34 shown in Table 1. These outcomes are obtained in remarkable achievement.
|
|
Khan and Hamid34
|
Ali and Zaib35
|
Current result
|
|
0.8
|
-1.26148
|
-1.26121
|
-1.26069
|
|
1.2
|
-1.37785
|
-1.37763
|
-1.37771
|
Table 1 Comparing of
for unsteady parameter
with
.
The physical variables for
,
and
profiles are displayed graphically Figure 2–19. These physical parameters are kept constant entire study with their value n=0.2, We=0.3,
=0.1, M=0.4,
=0.1, Rd=0.4,
=0.4, Nb=0.3, Nt=0.3,Df=0.03,Sr=0.4,Pr=0.7, Sc=0.8,
=0.02 and
=0.8. Table 2 show the numerically result of various value of emerging parameter. Enlarging the value of We and n accelerates the skin friction. While it is noted that rate of Nusselt and Sherwood fall down by increasing value of Rd and k Table 3.
|
|
We
|
|
Rd
|
Sr
|
Df
|
K
|
|
|
|
|
|
0.1
|
0.1
|
0.1
|
0.1
|
0.1
|
|
0.1
|
1.0994
|
0.7033
|
0.2791
|
1.2285
|
|
0.3
|
0.5
|
|
|
0.4
|
|
|
1.2868
|
0.7893
|
0.2608
|
1.0964
|
|
0.5
|
1
|
|
|
0.7
|
|
|
1.474
|
0.8545
|
0.2554
|
1.018
|
| |
|
0.2
|
0.3
|
|
|
0.6
|
0.6748
|
0.4305
|
0.5207
|
1.7698
|
| |
|
|
|
|
|
|
0.7117
|
0.4505
|
0.4218
|
1.6704
|
| |
|
|
|
|
|
|
0.8174
|
0.5058
|
0.3115
|
1.603
|
| |
|
0.3
|
0.5
|
|
|
1.2
|
0.4172
|
0.223
|
0.7632
|
2.3029
|
| |
|
|
|
|
|
|
0.433
|
0.2676
|
0.6283
|
2.1581
|
| |
|
|
|
|
|
|
0.4758
|
0.2892
|
0.463
|
2.1014
|
Table 2 Comparison of Skin fraction (
,
) Nusselt (
) and Sherwood number (
) for various of n, we, Rd, Sr, Df, k.
|
|
Free stream velocity
|
|
Sheet surface(wall) temperature
|
|
a
|
Constant
|
|
Ambient temperature
|
|
b
|
Constant
|
|
Velocity component along x-axis and y-axis
|
|
|
Radiation Parameter
|
X
|
Coordinate along the sheet
|
|
|
Brownian diffusion coefficient
|
Y
|
Coordinate normal to the sheet
|
|
|
Thermophoresis diffusion coefficient
|
|
Nano particle volume friction
|
|
|
Dufour number
|
|
Nano particle volume friction at the sheet surface (wall)
|
|
|
Magnetic field Parameter
|
|
Nano particle volume friction (ambient)
|
|
n
|
Power-law index
|
Greek symbol
|
|
k
|
Thermal conductivity of base fluid
|
|
Thermal diffusivity of the base fluid
|
|
Sr
|
Soret number
|
|
Unsteady parameter
|
|
Sc
|
Schmidt number
|
|
Nanofluid density
|
|
Nb
|
Brownian motion parameter
|
|
Fluid constant
|
|
Nt
|
Thermophoresis parameter
|
|
Dimensionless nanoparticle volume friction
|
|
Nu
|
Nussel tnumber
|
|
Dimensionless temperature
|
|
Nur
|
Reduced Nusselt number
|
|
Similarity variable
|
|
Pr
|
Prandlt number
|
|
Absolute viscosity of the base fluid
|
|
|
Wall heat flux
|
|
Kinematic viscosity of the base fluid
|
|
|
Mass flux
|
|
Density of base fluid
|
|
|
Local Reynolds number
|
|
Nanoparticle mass density
|
|
Sh
|
Sherwood number
|
|
Heat capacity of fluid
|
|
Shr
|
Reduced Sherwood number
|
|
Effective heat capacity of the nanoparticle material
|
|
T
|
Local fluid temperature
|
|
|
|
|
Temperature of the hot fluid
|
|
Stream function
|
Figure 2–4 are displayed to views the result of (n) on
,
,
and
. From the Figure 2 dimensionless velocity and concentration was reduced for the increasing value of (n). Actually, higher value of n boosts to improved the pressure on the flow results reduction in velocity and concentration and increment in thickness of layer and solutal boundary layer. Figure 5–7 have revealed to view the unsteady parameter (
) velocity
,
, temperature
and concentration of nanoparticle
. An increasing behavior in the nanofluid velocity component and boundary layer thickness enhanced due to the larger value of unsteady parameter. Due to this reason, unsteady variable is directly relative to the stretching rate of nanofluid with x-direction. Because escalated the unsteady variable the stretching rate with x-axis increases causes to upsurges nanofluid. Similar, behavior is seen for thermal and nanoparticles concentration. Figure 8–10 displays the of (We) on
,
,
and
. Figure 8 larger the value of We upsurge in momentum layer and velocity. It is a fact that We is a thermal relation time to increase more flow of fluid. From Figure 9 is plotted to view that temperature of nanofluid is augmented for the greater value of We. Physically, an enhanced in thermal relaxation process result the increased in fluid temperature. From Figure 10 is sketch to clear that concentration of nanoparticles is intensified for increment value of We. Figure 11–13 shows the
,
and
for the variation of A. It is noted that from Figure 11 when (
>1), the flow made boundary layer structure, from the fact that the shear effect toward the stagnation section accelerated so the augmentation of the outer stream enhances results diminish the thickness of the boundary layer causes larger magnitude of
. When (
<1). For
=1 there is no boundary layer structure is noted for the reason that both free stream and stretching velocity are equal. Velocity filed
increases with greater value of
. From Figure 12 and Figure 13 show that both θ(η) and ϕ(η) increases due to rise in
.
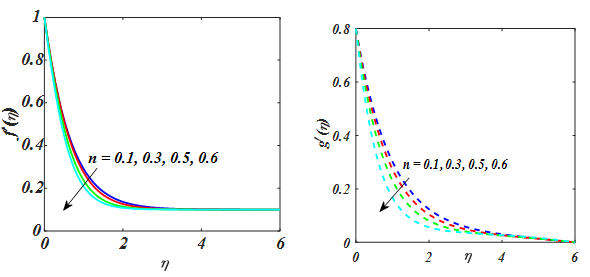
Figure 2
and
for value of n.
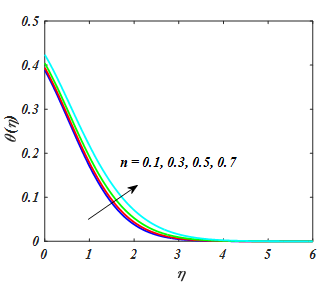
Figure 3 Θ for value of n.

Figure 4 Θ for value of n.
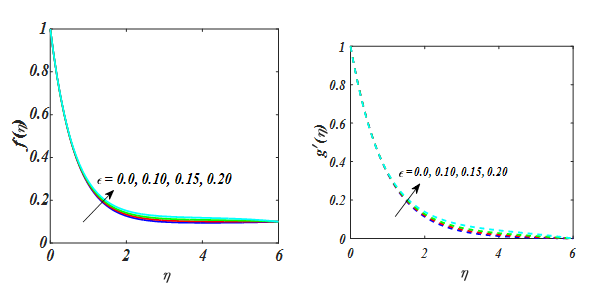
Figure 5
and
for value of
.
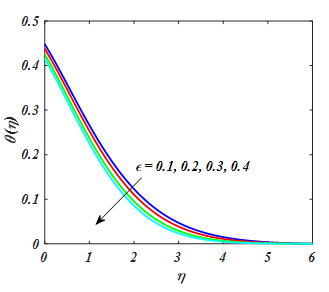
Figure 6
for value of
.
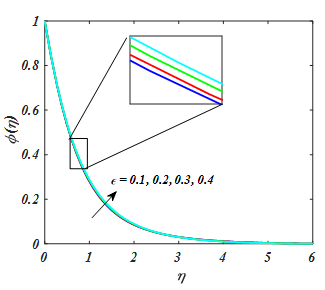
Figure 7
for value of
.
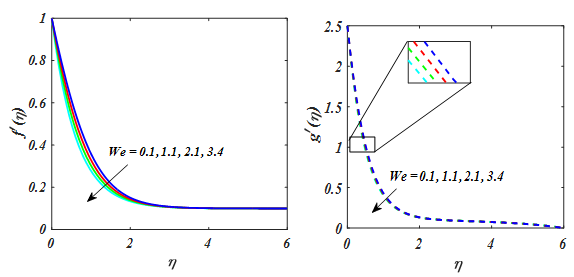
Figure 8
and
for value of We.
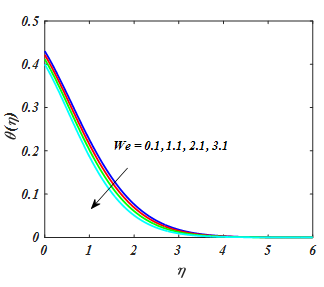
Figure 9
for value of We.
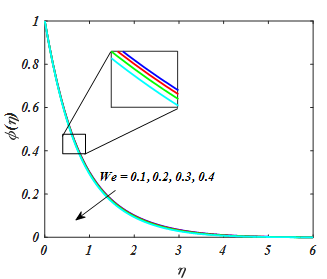
Figure 10
for value of We.
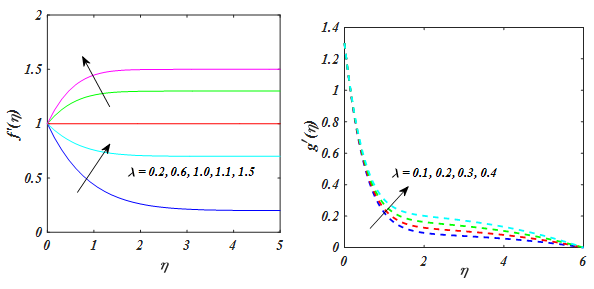
Figure 11
and
for value of
.
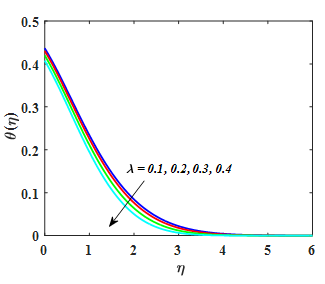
Figure 12
for value of
.
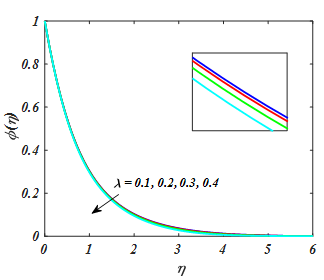
Figure 13
for value of
.
A significant of Nt and Nb for temperature and concentration of nanoparicle are explored in Figure 14–17. From Figures. the θ(η) and ϕ(η) distribution is increased for increasing value of Nt. From Figure 16,17 shown that the Nb boosts the temperature and reduced the concentration of nanoparticle. A fluid particle intensifies with augmentation in Nb and more heat is formed to amplify the thermal layer thickness. While enlarging value of Nb reduces nanoparticle concentration. Physically, boost in the magnitude of Nb result to enhance the rate of diffusions of nanoparticles in the base fluid motion in irregular direction. So, motion of nanoparticles escalates in convey of heat and decline in concentration.
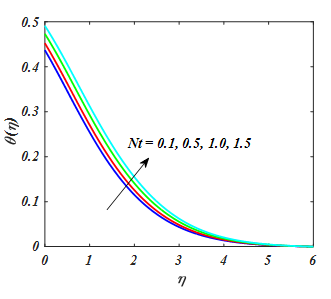
Figure 14
for value of Nt.
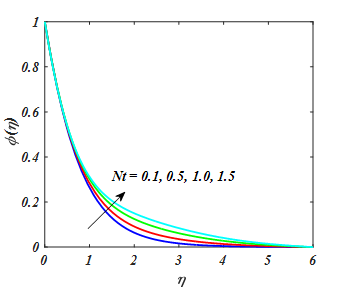
Figure 15
for value of Nt.
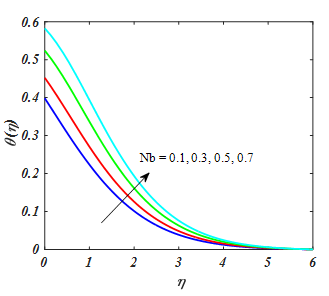
Figure 16
for value of Nb.
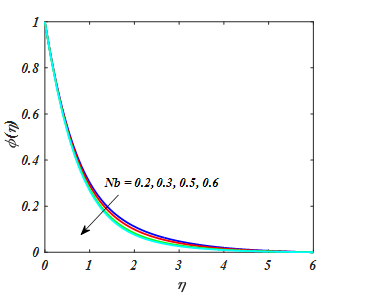
Figure 17
for value of Nb .
Figure 18 exhibits the effect of (Pr) on θ(η). Clearly from Figure 18 larger Pr fallout temperature profile whereas the fluid become more viscous. Consequently, fluid with a less viscosity obtained a leading temperature and greater viscosity produced the lesser temperature. So, by growing in Pr leads to thermal diffusivity which decline temperature of tangent hyperbolic fluid. The θ(η) for the variation of Rd has been exhibited in Figure 19. It describes that increase in temperature leading function of Rd. Physically, higher the radiation parameter Rd heat is produced in working fluid that is the reason temperature gradient accelerates. Temperature profile for diverse values of Ec has been indicated in Figure 20. Fluid temperature escalates for larger value of Ec. In this regard the increment in Eckert number Ec results increase in internal source of energy and that is the reason fluid temperature rise.
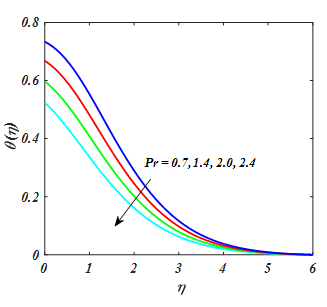
Figure 18
for value of Pr.
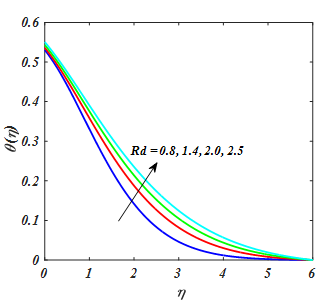
Figure 19
for value of Rd.
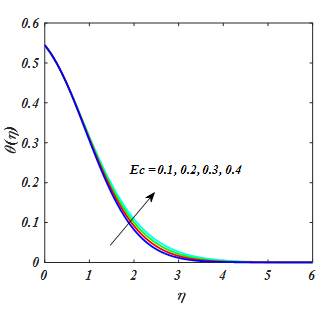
Figure 20
for value of Ec.
Figure 21,22 depicted the effect of Sc and k on nanofluid concentration. It is not able that an augment k and Sc has a trend to decline the nanofluid concentration.
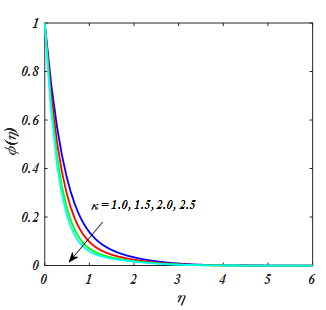
Figure 21
for value of K.
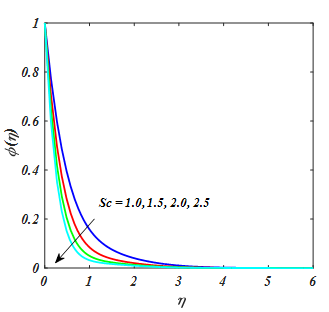
Figure 22
for value of Sc.
The effect of n and We on
,
wass illustrated in Figure 23,24. It shows that the
,
upsurges in favour of the different value of n and We. The persuade of Rd and Df on
is revealed in Figure 25. It is clear from the Fig. that the
depreciates for larger value of Rd and Df. The impact of k and Sr on
was seen in Figure 26.
reduced for greater value of k and Sr. Figure 27 shows the plot of stream line pattern for We and n.
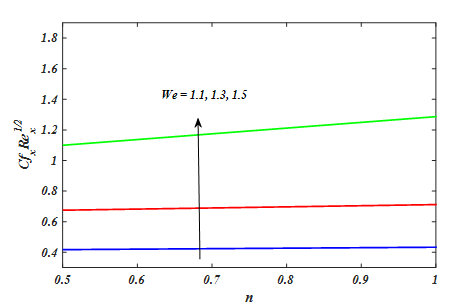
Figure 23 The impact of n and We on
.
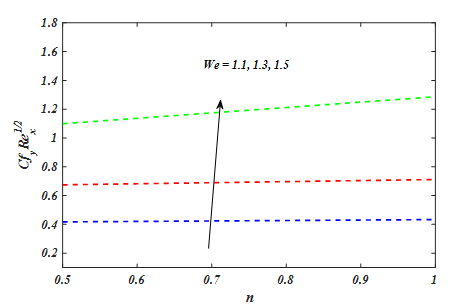
Figure 24 The impact of n and We on
.

Figure 25 The impact of Df and Rd on
.
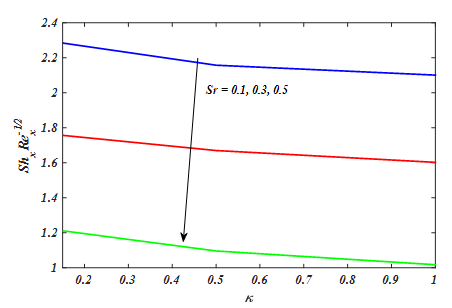
Figure 26 The impact of n and We on
.

Figure 27 Stream line Pattern for n and We.


