In this work, a gas-filled 1D elastic pneumatic photonic crystal is proposed as an optical indicator of pressure which can unite several pressure scales of magnitude. The indicator includes layered elastic platform, optical fibers and switching valves, all enclosed into a chamber. We have investigated the pneumatic photonic crystal band gap structure and light reflection changes under external pressure. At the chosen parameters the device may cover the pressure interval (0, 10) bar with extremely high accuracy (1 μbar) for actual pressures existing inside the biofluid systems of biological organisms. The size of the indicator is close to 1 mm and may be decreased. The miniaturized optical devices considered may offer an opportunity to organize simultaneous and total scanning monitoring of biofluid pressure in different parts of the circulatory systems.

Keywords: photonic crystal, optical devices, elastic layered structure, light reflection, precise pressure measurement, blood pressure

PhCr, photonic crystal; OPM, opto-pneumatic medium; EMF, electromagnetic field; TIR, total internal reflection

The artificial periodic structures like layered photonic crystals may serve as a means of measurement for the processes periodic in time peculiar to living organisms. There are a lot of periodic phenomena concerned with the blood and lymph system functioning in a living body. One of them is so called Mayer waves of pressure in arteries caused by oscillations in human receptor control systems.^1–3 The time dependinged processes of such kind and many other reasons like nature of the hypertension manifestations put forward precise pressure indicators as important optical instruments in the Biometry.^4,5 The fine structure of pressure and local temperature time dependencies would make clear the nature of processes in human body. Though the outstanding optical features of photonic crystals have been first mentioned in Rayleigh study,⁶ a tide of the modern applications in a wide area was began from works of Eli Yablonovitch & Sajeev John.^7,8 Various properties of photonic structures useful to create perfect dielectric mirrors, high-performance optical filters, key elements of logic gates, controlled mirrors or flexible waveguides and for many other applications were discussed since then.^9–13 In this study, we focus on the use of opto-mechanical properties of the pneumatic photonic medium as a means to indicate pressure during a time depended process inside the flood flow.

The opto-pneumatic medium as a multiscale pressure indicator

The pneumatic photonic crystals can exhibit significant optical sensitivity to variations of the external pressure and/or temperature.^14,15 It was shown there that a gas-filled 1D elastic photonic crystal may be used as an optical indicator with several measuring scales which may be organized on the same substrate due to the well expressed identity of the band gap structure behaviour. Here, we study a possibility to apply the pneumo-optical effects arising in a strip pneumatic photonic crystal to precise measurement of pressure inside a pipe with fluid flow. The system under consideration is shown in Figure 1A. It is a 1D strip photonic crystal consisting of one substrate made long thin layers of a transparent elastic material of width d₁ divided by air voids (d2) which can vary the lattice period under the action of the external pressure. The light beam reflects at the incident angle θ_l from the resonator center in longitudinal normal plane. The strip length is L and strip half widths are R_A and R_B, for PhCr’s A and B, correspondingly. We assume that for the photonic crystals under consideration the all strips widths 2R are much lesser than the strip length L and at the same time the laser beam cross-section size is considered as much lesser than the strip widths. Therefore, we can neglect the non-planarity of surfaces in the area of light beam incidence. Also, the strip design allows the beam inclined incidence in the longitudinal normal plane. In Figure 1A, a general schematic of a 2-scale pressure indicator based on a layered OPM is shown. The stack of plates contains two strip pneumatic photonic crystals A and B which embraces two scales of pressure indication covering several orders of magnitude. The access to the atmosphere is controlled with the help of switches 1 and 2. Geometry of light beam incidence is shown for strip A. The plate deflection ξ, being directed along the vertical z-axis is a function of the plate coordinates (x, y). In general case the equation for ξ was studied in.¹⁶

$D{\Delta }^2\xi =\delta P$ (1)

where the stiffness parameter of the plate D=Ed₁³/(12(1-σ²)), E is the Young modulus, and σ is the Poisson’s ratio; δP is the pressure difference. For our mathematically 1D case the Laplace operator is written as d²/dx² and, following,¹⁶ one can find the solution of (1) satisfying the edge boundary conditions for a fixed long separate elastic strip plate.^14,15 A stack of N optically transparent thin plates divided by closed air voids is a system, whose optical properties depend on the external pressure and temperature. Initially, the pressures inside the system coincide with the external pressure and for the above mentioned geometry of incidence we have a 1D photonic crystal with period d₀=d₁+d₂ and the corresponding reflection coefficient R(P0), where P0 is the external pressure The increase of the external pressure causes the compression and a decrease in the thickness of air layers d₂, which changes, in turn, the total reflection pattern. Combining pressures and volumes in neighbouring air voids divided by elastic plates, we arrive at a chain of equations

$P_i=\frac{Q{P}_{00}}{Q-P_{i-1}+2P_i-P_{i+1}}$, i-1,2,3,….N (2)

Where Q=45Dd₂/R⁴ is the effective elastic pressure of a plate, _P00 is the initial pressure of the device calibration. It is worth noting that boundary conditions of the system (2) may be chosen as P_N+1=P₀ in case of two-sided access of external pressure to the PhCr and P_N+1=P₀₀. In the limit when the number of plates is large enough, system (2) describes a continuous pneumatic medium^14,15with distributed air pressure inside and corresponding deformation of the PhCr. In Figure 1B, a scheme of one-sided measurement of pressure in a fluid-filled pipe is shown where the PhCr body 1 is placed into the closed chamber 2 penetrating through the pipe membrane in biofluid. The strip A device represents a scale of first level embracing interval (10, 10⁴ ) mbar, whereas the scale B serves to measure more fine-tuned dynamical changes. Another scheme of measurement - two-sided, supposes a free access of measured pressure to the upper chamber 2 and possesses higher sensitivity in comparison with one-sided one.

Figure 1 (A) A layered OPM as a multiscale pressure indicator schematically. A stack of plates contains two strip pneumatic photonic crystals A and B. 1, 2 are switches of access to upper gaseous medium (chamber) atmosphere. Geometry of light beam incidence is shown for strip A. (B) A sketch to the one-sided measurement of pressure in a pipe. 1, PhCr body, 2, upper chamber wall, 3, pipe membrane 4, 5, input-output fibers (light beams), 6, 7, switching elements of pressure access.

The opto-pneumatic medium as a multiscale pressure indicator

We will consider p-polarized electromagnetic field in the compressed 1D PhCr pneumatic structure consisting of N periods of glass plates divided by air voids. The declared problem can be considered in external and internal variants. The first one corresponds to external incidence of light beam whereas the latter touches standing EMF waves trapped inside the TIR. In Figure 2 (vertical panel), the band gap structure of glass/air 16 period 1D PhCr is shown inside the propagation angle interval (44°, 54°) of the TIR region at photon energies between 0 and 1.4 eV. The width of glass plates was taken d₁=0.5 μm and air voids d₂=0.8 μm at initial external pressure of calibration P=P₀₀=1 bar, glass dielectric function ε₁=2.1. The band gap structure exhibits 16 trapped modes in every band. According to Figure 1A, the first one is placed in the interval ωε (0, 0.71) eV at θ₁=44° whereas in upper part at θ₁=54° the band is narrowed and now occupies the interval of energies (0.78, 0.99) eV. The second band begins with 1.15 eV at θ₁=44°. It is clear from Figure 2 that on the boundary of the total internal reflection area and area of external incidence in vicinity of θ₁~90° a typical whispering reflection arises which replicates the beginning of the bandgap structure inside the total internal reflection region on vertical panel. In Figure 2 (horizontal panel), the calculated reflection color diagram is presented at the horizontal panel in energy interval (0 – 1.4) eV and angular interval θ_lε (0º – 90º). An all-energy transparency band near 54.4° illustrates the well known Brewster effect.

Figure 2 Vertical panel: the bandgap structure of glass/air 1D PhCr inside TIR region at the propagation angles θ1in glass from 44° to 54°. N=16, d1=2 μm, d2=2 μm, photon energy up to 1.4 eV. Horizontal panel: color diagram for reflection R of the external incident beam at external (air medium) incident angles θlfrom 0° to 90°. Right column: color scale for reflection coefficient R.

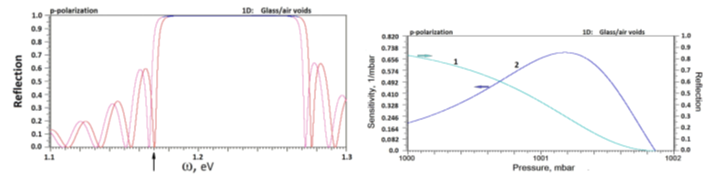
Both the band gap structure and reflection map of the OPM are strongly dependent on the external pressure in two variants of measurement – one-sided (Figure 1B) and two-sided. Taking into account the chain of correlations (2) we have calculated the pressure influence on the EMF interaction with a deformed photonic crystal. With the pressure growth, bands were destroing and local states have been arisen. In Figure 3A, the calculated reflection at quasi-normal incidence is plotted in energy interval (1.1 -- 1.3) eV for a 15 period glass/air OPM with parameters d₁=0.5 μm and d₂=0.8 μm at quasi-normal angle of incidence θ_l=1º. In this case, the reflection window (frequency gap) is observed in energy interval (1.17 -- 1.27) eV. Due to elasticity of OPM, any change of external pressure is accompanied with a shift of the frequency gap. One of the gap sides can be used as the working frequency. We choose the low energy edge of the gap with ω=1.17 eV (Figure 3A arrow). In Figure 3B, we calculate reflection measured by device B at chosen photon energy ω=1.17 eV for pressure interval (1000 – 1002) mbar where the reflection coefficient decreases from 0.83 to zero (curve 1). The isothermal sensitivity η=(dρ/dP)_T changes from zero at P=1001.86 mbar to the maximal magnitude 0.698 mbar^-1 at P=1001.18 mbar.

Figure 3 (A) Quasi-normal incidence (θl=1º) reflection vs photon energy. Two-sided measurement. 15 period glass/air 1D PhCr. d1=0.5 μm, d2=0.8 μm. Energy gap (R≈1) is distinguished by color; arrow shows the chosen operating energy ω=1.17 eV. (B) Reflection sensitivity vs pressure. Quasi-normal incidence, fixed photon energy ω=1.17 eV (arrow). 1, reflection vs pressure dependence (right axis), 2, sensitivity vs pressure dependence (left axis).

Fine structure of pressure in a fluid flow

We have discussed above two ways of organizing the measurement procedure: one-sided acting pressure as it is shown in Fig. 1b and top-bottom acting pressure (two-sided) when measured fluid pressure inside the pipe is transferred into the upper chamber of the device. As a result, the deformation of elastic plates inside the PhCr is symmetric relatively its body’s center. Due to well expressed scale invariance of the band gap structure¹⁴for a 1D PhCr an opportunity exists to unite on a substrate several OPM devices which have identical calibration scales for different intervals of the measured physical quantity (Figure 1A). In our case, for the chosen parameters the first pressure calibration curve occupies interval (10 -10^-2) bar (A, R=200 μm). The interval of measured pressures for the second device B (R=300 μm) embraces interval (10^-2 -10^-5) bar in area close to 1000 mbar with average accuracy 1 μbar. During the second, compensating, stage of the measurement procedure^14,15some μbar corrections will be added to result obtained at scale A.

From a physical point of view, any living organism is an extremely complicate system of pipes with flowing biofluids inside. The pressure pattern is controlled by several intrinsic biological pumps and differs for different parts and organs depending on health and other factors. Together with temperature, their distribution inside parts of the body, their time dependencies are important characteristics for describing normal or abnormal functioning of the human organism. Here, we have discussed the possibilities of the gas-filled elastic photonic structures as sensitive optical indicators which can unite several pressure scales of accuracy. The indicator includes layered elastic platform, optical fibers and switching valves, all enclosed into a chamber. At the chosen parameters the device may cover the pressure interval (0, 10) bar with extremely high accuracy (1 μbar) for actual pressures existing inside the biofluid systems of biological organisms. The size of the indicator is close to 1 mm and may be decreased. The miniaturized optical devices considered above may offer an opportunity to organize simultaneous and total scanning monitoring of biofluid pressure in different parts of the circulatory systems.

None.

Authors declare that there is no conflict of interest.

1. Julien C. The enigma of Mayer waves: Facts and models. Cardiovasc Res. 2006;70(1):12–21.
2. Elghozi JL, Laude D, Girard A. Effects of respiration on blood pressure and heart rate variability in humans. Clin Exp Pharmacol Physiol. 1991;18(11):735–742.
3. Takalo R, Korhonen I, Turjanmaa V, et al. Short-term Variability of Blood Pressure and Heart Rate in Borderline and Mildly Hypertensive Subjects. Hypertension. 1994;23:18–24.
4. Optical Biomimetics: Materials and Applications. In: Maryanne Large, Editor. Woodhead Publishing; 2012. 256p.
5. Zamir M, Moore JE, Fujioka H, et al. Biofluid mechanics of special organs and the issue of system control. Ann Biomed Eng. 2010;38(3):1204–1215.
6. Rayleigh JW. On the maintenance of vibrations by forces of double frequency and on the propagation of waves through a medium endowed with a periodic structure. Philos Mag. 1887;24(147):145–159.
7. Yablonovitch E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Physical Review Letters. 1987;58(20): 2059–2062.
8. John S. Strong localization of photons in certain disordered dielectric superlattices. Physical Review Letters. 1987;58(23):2486–2489.
9. Werber A, Zappe H. Tunable, membrane-based, pneumatic micro-mirrors. J Opt A: Pure Appl Opt. 2006;8:313–317.
10. Pervak V, Ahmad I, Trubetskov MK, et al. Double-angle multilayer mirrors with smooth dispersion characteristics. Opt Express. 2009;17(10):7943–7951.
11. Tokranova N, Xu B, Castracane J. Fabrication of flexible one-dimensional porous silicon photonic band-gap structures. MRS Proceedings. 2004.
12. Grzybowski B, Qin D, Haag R, et al. Elastomeric optical elements with deformable surface topographies: applications to force measurements, tunable light transmission and light focusing. Sensors and Actuators. 2000;86(1-2):81–85.
13. Ouellette J. Seeing the Future in Photonic Crystals. The Industrial Physicist. 2002;7(6):14–17.
14. Glushko EY. Pneumatic photonic crystals. Opt Express. 2010;18(3):3071–3078.
15. Glushko EY. Pneumatic photonic crystals: properties and multiscale indication of pressure. Proc of IEEE CAOL Conference. 2010:36–37.
16. Landau LD, Lifshitz EM. Theory of Elasticity. New York: Pergamon Press; 1970. 65p.