Meta-population models are relevant to understand the dynamics of a species which often persists in highly fragmented landscapes. It was hypothesized that the probabilities of species colonization and extinction rates of meta-populations on island system could be affected by fraction of islands occupied and size of each island. Using meta-population models, probabilities of colonization and extinction rates of the endemic lava heron (Butorides sundevalli) were computed to evaluate the dynamics of meta-population on the archipelago island system and later to interpret the ecological processes attributed for such dynamic nature. The results revealed that islands which are large in size showed a source-effect due to their positive internal rate of population growth, lower probabilities of extinction rates, and higher average abundance of population size. However, islands with small size had lower average abundance of population size and relatively lower (i.e. negative) internal rate of population growth so that they acted to play a sink-effect. The comparison across the twelve islands showed that both probabilities of colonization and extinction rates of small sized islands were relatively higher than those islands with large size. The extinction probabilities increased with the increase in fraction of occupied islands, but colonization probabilities showed a slight decline when the fraction of occupied islands increased. Fraction of islands occupied and area of islands had significant effect to predict the internal rates of population growth and the average abundance of population size, respectively. The study suggested that the meta-population structure of the endemic lava heron on the archipelago island system was found to be a combination of source-sink and core-satellite structure. Therefore, future conservation strategies should not only consider the number of individuals of a species found over a landscape, but also the spatial distributions, rates of colonization and extinction of a species in different habitat patches across the landscape of concern.

Keywords: archipelago, colonization, core-satellite, extinction, island system, source-sink

Ecological studies on the distribution, abundance, species richness, and population dynamics of organisms are currently becoming hot issues in ecology and evolutionary biology because they are the bases specifically for the conservation of endangered and threatened species at local and regional scales.^1,2 For example, meta-population dynamics is one of the recent ecological concepts dealing with the probabilities of species colonization and extinction rates on different landscapes including the island system.^3,4 A meta-population refers to a population inhabiting a collection of discrete patches.^5,6 The probabilities of colonization and extinction rates of meta-population on the archipelago island system could be affected by the fraction of islands occupied, the size of each island, and distance between or among islands and/or the mainland. This is because dispersal rate and colonization of populations of a species on a specific island is affected by its isolation (i.e. distance) from the mainland as a source-sink effect.^7–9 The concept of a biota in a contemporary equilibrium between colonization and extinction was also challenged by new finds of fossils.^3,6 This suggested that it has not kept pace with relevant theory and our growing appreciation for the complexity of nature, especially with empirical findings that species diversity on many islands. This is because most islands are not in stable equilibrium as they are influenced by differences in speciation, colonization, and extinction among taxa; and also influenced by differences among islands in characteristics other than area and isolation (i.e. distance).³ Moreover, variation in size and quality of patches⁷ and variation due to different spatial arrangement of patches would have different effects on population dynamics.^9–11

Meta-population models are important tools to understand the distribution and abundance of organisms on large spatial scales.^3,4 This is because meta-population models describe an open system, in which extinction and colonization depends on the movement of individuals among a set of patchy sites.^5,9,11 Those models are especially relevant to understand the dynamics of endangered species which often persist in highly fragmented landscapes.¹² The dynamics of species living in fragmented landscapes has produced much information on the patterns of habitat patch occupancy in a wide range of organisms.^5,13 A lot of attempts were made to develop various models to test the meta-population dynamics largely relying on Monte Carlo simulations.¹⁴ For example, Anderson (1991) considered a stochastic continuous time meta-population model which explicitly models the size of each local population in a collection of variable sized patches. Presence-absence data for meta-populations were also used to estimate probabilities of patch extinction and colonization.¹⁶ Of course, all over the world, species have faced loss and fragmentation of their natural habitats by anthropogenic factors. ^9,12,16–19 The extinction of a species involves elements of chance. Hence, it is important to include stochastic influences when modeling a meta-population occupying a small number of patches.^3,5,9 Various meta-population models also predicted that the occurrence of core-satellite structure.^4,7,20 in natural system so that it is crucial to conserve meta-populations with different abundance-incidence parameters and playing as source-sink effect.^14,20,21 Most empirical ecologists that use meta-population concepts prefer to use the simpler Levin’s model as it requires the least assumptions because it needs only colonization and extinction rates to be known.^4,22 Moreover, attempts made to find meta-populations in nature have been hampered by the difficulty in measuring the needed parameters and the amount of time required documenting reproduction, dispersal, extinction, and colonization.²³

The lava heron (Butorides sundevalli) is one of the endemic species refuging in the archipelago island system of Ecuador.²⁴ However, only little is known about the species with respect to its population dynamics, rates of colonization and extinction on the island system. It was hypothesized that the probabilities of species colonization and extinction rates of meta-populations on island system could be affected by fraction of islands occupied and size of each island.^3,4,23 Here I considered the twelve archipelago islands whose sizes are: 25, 35, 110, 115, 117, 120, 140, 150, 265, 285, 370, and 431 hectares, respectively. The size of those islands ranges from 25 to 431 hectares. The objectives of the study were to: (1) determine the meta-population dynamics of the endemic lava heron on the archipelago island system through estimating the probabilities of colonization and extinction rates; and (2) investigate the structure of meta-populations and their trends on the island system by using meta-population models. Hence, the following two questions were addressed: (1) how can we determine the meta-population dynamics of the endemic lava heron on the archipelago island system through estimating the probabilities of colonization and extinction rates? And (2) how can we investigate the structure of meta-populations and their trends on the island system by using meta-population models?

Study site

The study was conducted on the archipelago islands of Ecuador. It was carried out to deal with the little studied endemic lava heron (Butorides sundevalli). Through the application of meta-population models, the present study is crucial to determine population dynamics, rates of colonization, and extinction of lava heron on the island system.

Statistical tests

On top of contributing to the conservation of species, meta-population models are relevant to understand the dynamics of endangered species which often persist in highly fragmented landscapes found in the archipelago island system.^1,2 With the assumption of equi-distances among the twelve islands for equal probabilities of colonization and extinction rates, the thirty years data were analyzed using mathematical models developed by meta-population ecologists.^3,4,23 Accordingly, probabilities of colonization and extinction rates of the endemic lava heron on each island were computed to evaluate the dynamics of meta-population on the archipelago island system and later to interpret the ecological processes contributed to the dynamic nature on the island system. Thus, an occurrence matrix was constructed in which each row was used as a year whereas each column was treated as an island. In this matrix, an entry of one represents the presence of a population in the island during that particular year whereas a zero indicates the species was absent in that specified year in the island. Following Gotelli and Taylor (1999), I calculated f, the fraction of islands occupied, as: f = number of islands occupied in year (t)/number of islands that were censused in year (t). For each island, I also calculated the least square regression slope of the probability of extinction versus the fraction of islands occupied. Moreover, I tested whether the probability of local extinction decreases significantly as more islands were occupied. Next, I calculated the probability of colonization (pi) for each island as followed. pi = number of unoccupied islands in year (t) that were occupied in year (t+1)/the number of islands that were censused in year (t). For each island, I also calculated the least square regression slope of the probability of colonization versus the fraction of islands unoccupied. Hence, a t-test was used to evaluate the statistical significance of the regression slope.

I also calculated pe, the probability of extinction between each pair of consecutive years as followed. pe = number of islands occupied in year (t) that were unoccupied in year (t+1)/number of islands occupied in year (t). Hence, for the census data of the 30 years, there were 29 annual probabilities of extinction that could be calculated. Moreover, I calculated the internal rate of population growth for the endemic lava heron on each island. This activity is important to evaluate the effect of internal rate of population growth on meta-population structure as source-sink effect.^14,20–22 Accordingly, the internal rate of population growth on each island was calculated as followed:

r = b - d

Where,

r = internal rate of population growth for each island

b = birth rate on each island

d = death rate on each island

Finally, I calculated the average abundance of lava heron population on each island over the thirty years’ time span. Therefore, average abundance = the summation of the populations on each island over the thirty year time/30.

Testing the premises of meta-population models

The two basic premises of meta-population models were tested with the results obtained from the analyzed data. One of the premises is that meta-population has reached an equilibrium state in which local extinctions are balanced by local colonization.^4,23 Thus, if equilibrium has not been reached, probabilities of extinction and colonization rates will change with time. To test this premise, I first computed the probabilities of colonization (pi) and extinction (pe) over the 30 years period. Next, I measured the slope of the relationship between probabilities of colonization (pi) and extinction (pe) rates across the twelve islands. Hence, the null hypothesis is that the slope does not significantly differ from zero. The second premise was taken from Levins-style⁵ meta-population models whose premise was that islands are homogenous so that the probabilities of local colonization (pi) and extinction (pe) rates are the same across all islands. In this study, the size of each island is different (i.e. 25, 35, 110, 115, 117, 120, 140, 150, 265, 285, 370, and 431 hectares, respectively) so that it is more likely to affect the probabilities of colonization (pi) and extinction (pe) rates. Thus, I calculated the probabilities of colonization (pi) and extinction (pe) rates across the twelve islands, and evaluated whether these probabilities were significantly correlated with the size of the twelve islands. For all analyses, I defined the alpha value to be 0.05 and performed the analyses with STATISTICA version 10.

The results revealed that the fraction of islands occupied (f) across the 12 islands on the archipelago island system had a mean value of 0.44, SE = 0.10; a maximum value of 0.58, a minimum value of 0.25, and a range value of 0.33. The results further showed that the probability of colonization (pi) across the 12 islands had a mean value of 0.23, SE = 0.02; a maximum value of 0.50, but the minimum value was 0.00 whereas the range was 0.50. With regard to the probability of extinction (pe) across the 12 islands, the mean, the maximum, and the minimum values were 0.28, 0.67, and 0.00, respectively; with SE = 0.03 and a range of 0.67 (Table 1). The results suggested that the fraction of islands occupied (f) over the 30 years period on the archipelago island system had a mean value of 0.44, SE = 0.02; a maximum value of 0.97 whereas the minimum value was 0.07, but the range was 0.90. The results further showed that the probability of colonization (pi) over the 30 years period on the island system had a mean value of 0.13, SE = 0.03; a maximum value of 0.24, but the minimum value was 0.03 with a range of 0.21. With regard to the probability of extinction (pe) over the 30 years period on the island system, the mean, the maximum, and the minimum values were 0.13, 0.28, and 0.03, respectively, but SE = 0.04; and the range was 0.25 (Table 1). The internal rate of population growth (r) over the 30 years period on the island system had a mean value of 0.0002, SE = 0.01; maximum value of 0.03, and a minimum value of -0.02, but the range was 0.05. Furthermore, the average abundance of lava heron population on each island over the 30 years’ time span had a mean value of 5.35, SE = 2.04; whereas the maximum and minimum values were 19.6 and 0.1, respectively, but the range was 19.5. The overall frequency of the lava heron population across the twelve islands over the 30 years period was 0.44 (Table 1).

In contrast to the prediction of the meta-population models, the results of the present study suggested that the probability of colonization showed a negative regression slope (-0.0293) (Figure 1) though the fraction of islands occupied (f) increased over the 30 years span. This suggested that the null hypothesis was accepted because the slope of this correlation was very close to zero as the P value was (P = 0.25). Moreover, the results showed that the probability of colonization (pi) did not differ with the fraction of islands occupied (f) over the 30 years period, implying a constant propagule rain. The prediction of simple meta-population models suggested that the probability of extinction is positively influenced by the rescue effect. This means that the probability of extinction should decrease as a fraction of islands occupied increased. However, the results of the present study showed that the probability of extinction increased as the fraction of islands occupied (f) increased over the 30 years span. This is in contrast to the prediction made by the meta-population model of the rescue effect because the probability of extinction showed a positive regression slope (1.5267) (Figure 1) which was significantly different from zero as the P value was (P < 0.001).

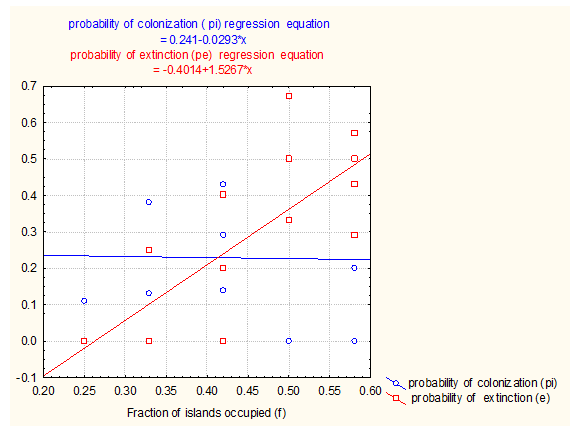
Figure 1 The probabilities of colonization (pi) and extinction (pe) of the population of the endemic lava heron (Butorides sundevalli) as a function of the fraction of islands occupied (f) over the 30 years’ time span.

In line with the prediction made by the meta-population model, the average abundance of population on each island (N) increased with the increase in the fraction of islands occupied (f) across the twelve islands because the average abundance of the population showed a positive regression slope (0.497) (Figure 2a) which was significantly different from zero as the P value was (P < 0.05). Moreover, the internal rate of population growth on the islands increased with the increase in the area of islands because the internal rate of population growth showed a positive regression slope (0.453) (Figure 2b) which was significantly different from zero as the P value was (P < 0.05). In the case of across islands comparison, both colonization and extinction probabilities showed a decline with the increase in the fraction of occupied islands because the probability of colonization showed a negative regression slope (-0.1059) (Figure 3a), but not different from zero as the P value was (P = 0.35). And the probability of extinction showed a similar negative regression slope (-0.0926) (Figure 3a) which was not different from zero as the P value was (P >0.05). The same trend was also observed on the probabilities of colonization (pi) and extinction (pe) as the area of islands increased because the probability of colonization had a negative regression slope (-0.1063) (Figure 3b) which was not different from zero as the P value was (P = 0.32). And the probability of extinction had also a negative regression slope (-0.1076) (Figure 3b) which was not different from zero as the P value was (P = 0.29).

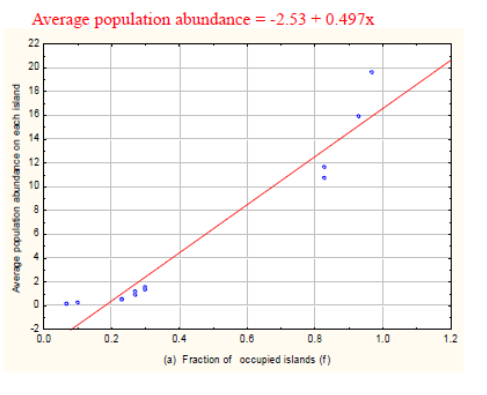
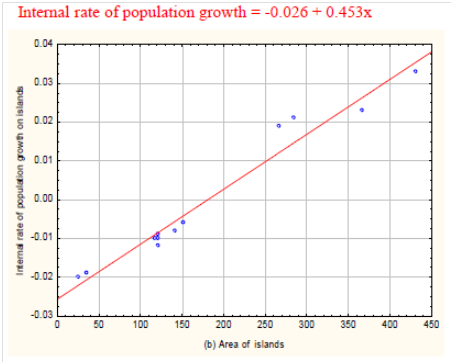
Figure 2 The average abundance of the population of the endemic lava heron (Butorides sundevalli) as a function of the fraction of islands occupied (f) (a), and the internal rate of population growth as a function of area of islands (b) across the twelve islands. The area of each island was expressed in hectares.

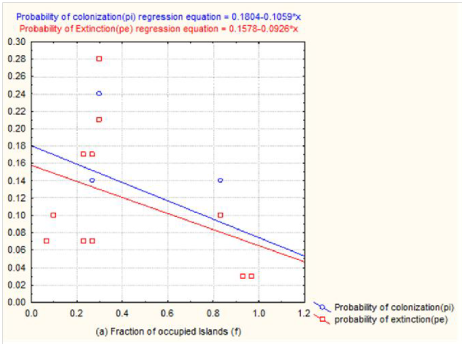
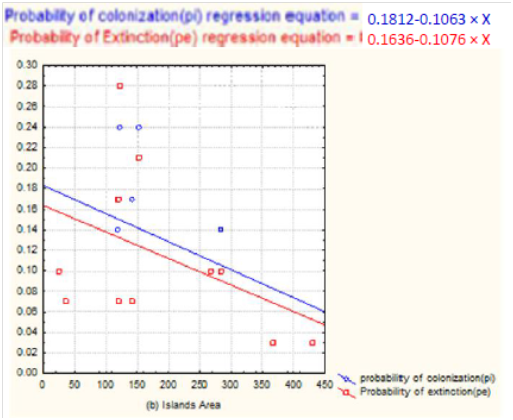
Figure 3 The probabilities of colonization (pi) and extinction (pe) of the population of the endemic lava heron (Butorides sundevalli) as a function of the fraction of islands occupied (f) (a), and probabilities of colonization (pi) and extinction (pe) as a function of area of islands (b) across the twelve islands.

Estimating the probabilities of colonization and extinction for meta-populations is a basis to look into the dynamics, abundance, and distribution of populations on the archipelago island system where species have faced a problem of habitat fragmentation followed by local extinction.^{2,13,16,17,21} It is also important to provide basic field information for the conservation of species with meta-populations that are liable to extinctions in different temporal scales but rescued through colonization.^4,13 With regard to the time frame comparison over the thirty years’ time, in contrast to the prediction made by the meta-population models, extinction probabilities increased with the fraction of occupied islands (f) though colonization probabilities showed a slight decline when the fraction of occupied islands increased (Figure 1). Gottile and Taylor (1999) also reported a similar result on eight species of fish while testing the meta-population model on the stream-fish populations where the result showed opposite to the prediction of the meta-population rescue effect. Perhaps this similar result for the endemic lava heron suggested that meta-population models are more appropriate for certain other taxa, such as butterflies^25,26 and shrews.²⁷

The first premise of meta-population model is to reach an equilibrium state when local extinctions are balanced by local colonization.²³ In the present study, it was estimated that the equilibrium state reached at 0.24 (Figure 1). However, the second premise of meta-population model which was suggested by Levins (1969) was violated in the present study because the probabilities of extinction and colonization were not homogenous (Figure 1). The results of the present study showed that average abundance of lava heron’s population increased when the fraction of islands occupied (f) increased (Figure 2a). This was in line with the prediction made by the meta-population models. This suggested that the average abundance of population (N) increased when islands were more occupied by individuals resulting from colonization from the nearby area (e.g. dispersal) or positive internal rate of population growth.^7–9 In line with the prediction made by meta-population models, the result further revealed that international rate of population growth (r) increased with the increase in the area of islands (Figure 2b). For example, according to Pulliam (1988), one of the possible reasons could be positive internal rate of population growth. The other reason is that the ecological niches on large islands are not filled so that there will be high reproduction as there is no resource limitation due to competition.²⁸ Generally, the results suggested that those islands with low average abundance of populations (N) and/or negative internal rates of population growth (r) are satellite populations whereas islands with high average abundance of populations (N) and/or positive internal rate of population growth (r) are core populations^4,7,20 on the archipelago island system.

The average abundance-incidence and distribution of lava heron across the twelve islands (Figure 2a, b) showed that there is a core-satellite meta-population. This is because islands with large size showed positive internal rate of population growth so that they are core populations²⁰ compared with islands with small size and negative internal rate of population growth (Figure 2b) which are satellite population in the meta-population dynamic model.^3,7 Generally, the results of the present study suggested that the meta-population structure of the endemic lava heron on the archipelago island system should be the combination of source-sink^4,23 and core-satellite^3,7,20 structure. Moreover, in natural systems, Pulliam (1988) and Hanski (1999) noted that meta-populations are distributed across their habitats depending on temporal and spatial variations whose effects cannot be explained by a single model. For example, various meta-population models also predicted that the occurrence of core-satellite structure in natural system so that it is crucial to conserve meta-populations with different abundance-incidence parameters and playing as source-sink effect.^13,14,20,21 Across islands comparison, both the probabilities of colonization and extinction rates showed a decline with the increase in the fraction of occupied islands (Figure 3a) and the same situation was also observed on the probabilities of colonization and extinction as the areas of islands increased (Figure 3b). This showed that islands with big area play a source-effect whereas islands with small area play a sink-effect.⁷

The decrease in the probabilities of extinction with the increase in islands area was in line with the prediction made by the meta-population models.^3,4,23 In the present study, the size of each island is different so that it is likely to affect the probability of colonization (pi) and extinction (pe). However, in contrast to the prediction of meta-population models,^3,4 the probabilities of both extinction and colonization decreased with the increase in the area of islands. One of the possible reasons is that colonization is more than just dispersal. For example, when a propagule reaches a new patch, it faces higher extinction probabilities than does an established population.^29,30 Gotelli and Taylor (1999) also noted that in the absence of meta-population dynamics, propagules could arrive from a large constant, e. g. ‘mainland’ source, in which case the probability of colonization would be independent of site occupancy (i.e. due to the island–mainland model). Various theoretical and empirical studies^{3,6–8,11,12,31} suggested that distances between or among adjacent islands and/or mainland (i.e. isolation), organismic behavior, speciation, locomotion ability of individuals of a species, and migration could substantially affect the probabilities of colonization (pi), extinction (pe), average abundance of population on each island (N), and internal rate of population growth (r) on the archipelago island system. Moreover, competition,²⁸ predation,⁹ natural and man-made barriers (e.g. topography, wind, climate change, and dams),²³ biological invasion,³² genetic variability and body size,³³ the relative position of each island in relation to other islands and/or mainland,^23,34,35 quality and spatial arrangements of patches (i.e. habitat heterogeneity and complexity),^9,36 and human-induced disturbances (logging, hunting, burning, habitat destruction and fragmentation, settlement, and livestock free-range grazing)^17,18,19 could influence the structure, distribution, and abundance of meta-population. However, due to lack of field data on all those aforementioned factors, the present study did not address them.

Meta-population models are relevant to understand the dynamics of endangered species which often persist in highly fragmented landscapes on the island system. The present study suggested that the meta-population structure of the endemic lava heron on the archipelago island system was found to be a combination of source-sink and core-satellite structure. Fraction of islands occupied and the area of islands had a significant effect to predict the internal rates of population growth and the average abundance of population size for the endemic lava heron on the archipelago island system, respectively. Therefore, conservation strategies should not only consider the number of individuals of a species found over a landscape, but also the spatial distributions, rates of colonization and extinction of a species in different habitat patches across the landscape of concern. Moreover, future study should incorporate all the factors explained in the discussion section while dealing with meta-population models to test and precisely predict pi, pe, N, and r values on the archipelago island system so that the models will ultimately enhance the conservation of endangered species including the endemic lava heron.

The author would like to forward his gratitude to Debre Berhan University for covering all sources of funding that helped in the analyses and interpretation of the data, and also writing the manuscript.

The author declares that there is no conflict of interest.

1. Morris DW, Kotler BP, Brown JS, et al. Behavioral indicators for conserving mammal diversity. Annals of New York Academy of Science. 2009;1162:334–356.
2. Primack RB. Essentials of conservation biology. 3rd edn. USA: Inc. Publishers, Massachusetts; 2002. 698 p.
3. Hanski I. Single-species meta-population dynamics: concepts, models and observations. Biological Journal of the Linnean Society. 1991;42:17–38.
4. Hanski I. Meta-population ecology. Oxford UK: Oxford University Press; 1999.
5. Levins R. Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull Entomol Soc Am. 1969;15:237–240.
6. Hanski I, Gilpin M. Meta-population dynamics: brief history and conceptual domain. Biological Journal of the Linnean Society. 1991;42:3–16.
7. Pulliam HR. Sources, sinks, and population regulation. The American Naturalist. 1988;132:652–661.
8. Harrison S. Long-distance dispersal and colonization in the Bay checkerspot butterfly, Euphydryas editha bayensis. Ecology. 1989;70:1236–1243.
9. Harrison S. Local extinction in a meta-population context: an empirical evaluation. Biological Journal of the Linnean Society. 1991;42:73–88.
10. Doak DF, Mills SL. A useful role for theory in conservation. Ecology. 1994;75:615–626.
11. Holt RD. A neglected facet of island biogeography: the role of internal spatial dynamics in area effects. Theor Popul Biol. 1992;41:354–371.
12. Wilcox BA, Murphy DD. Conservation strategy: the effects of fragmentation on extinction. The American Naturalist. 1985;125:879–887.
13. Hanski I. A Practical model of meta-population dynamics. Anim Ecol. 1996;63:151–162.
14. Hanski I, Thomas CD. Meta-population dynamics and conservation: a spatially explicit model applied to butterflies. Biol Conserv. 1994;68:167–180.
15. Anderson WJ. Continuous-time Markov chains. New York: Springer-Verlag; 1991.
16. Hanski I. Patch-occupancy dynamics in fragmented landscapes. Trends Ecol Evol. 1994;9:131–135.
17. Jagera HI, Chandlerb JA, Leplab KB, et al. A theoretical study of river fragmentation by dams and its effects on white sturgeon populations. Environmental Biology of Fishes. 2001;60:347–361.
18. Kebede AT. Sustaining the Allideghi grassland of Ethiopia: influence of pastoralism and vegetation change. USA: PhD dissertation. Utah State University; 2009. 309 p.
19. Tadesse SA, Kotler BP. The impacts of human and livestock encroachments on the habitats of mountain nyala (Tragelaphus buxtoni) in Munessa, Ethiopia. International Journal of Biodiversity and Conservation. 2013;5:560–571.
20. Schlosser IJ, Angermeier PL. Spatial variation in demographic processes of lotic fishes: conceptual models, empirical evidence, and implications for conservation. In: JL Nielsen, editors. Evolution and the Aquatic Ecosystem: Defining Unique Units in Population Conservation, American Fisheries Society, Bethesda. 1995. pp. 392–401.
21. Shaffer ML. The meta-population and species conservation: the special case of the northern spotted owl. U.S. Department of Agriculture, Forest Service, General Technical Report PNW. 1985;185:86–99.
22. Crone EE, Doak DF, Pokki J. Ecological influences on the dynamics of a field vole meta-population. Ecology. 2001;82:831–843.
23. Gotelli JN, Taylor MC. Testing meta-population models with stream-fish assemblages. Evolutionary Ecology Research. 1999;1:835–845.
24. Heinzel H, Hall B. Galapagos diary. 1st edn. Los Angeles: University of California Press; 2000.
25. Hanski I, Kuussaar M, Nieminen M. Meta-population structure and migration in the butterfly Melitaea cinxia. Ecology. 1994;75:747–762.
26. Hanski I, Pakkala T, Kuussaari M, et al. Meta-population persistence of an endangered butterfly in a fragmented landscape. Oikos. 1995;72:21–28.
27. Peltonen A, Hanski I. Patterns of island occupancy explained by colonization and extinction rates of shrews. Ecology. 1991;72:1698–1708.
28. Bengtsson J. Interspecific competition in meta-populations. Biological Journal of the Linnean Society. 1991;42:219–237.
29. Diamond JM. Colonization of exploded volcanic islands by birds: the supertramp strategy. Science. 1974;184:803–806.
30. Ebenhard T. Reproductive traits and body size as adaptations to a colonization strategy in field voles (Microtus agrestis). Ecology. 1990;71:1833–1848.
31. Schaffter RG. White sturgeon spawning migrations and location of spawning habitat in the Sacramento River, California. California Fish and Game. 1997;83:1–20.
32. Mollison D. Modeling biological invasions: chance, explanation, and prediction. Philosophical Transactions of the Royal Society of London. 1986;314:675–693.
33. Ebenhard T. Colonization in meta-populations: a review of theory and observations. Biological Journal of the Linnean Society. 1990;42:105–121.
34. Osborne LL, Wiley MJ. Influence of tributary spatial position on the structure of warm water fish communities. Can J Fish Aquat Sci. 1992;49:671–681.
35. Taylor CM. Fish species richness and incidence patterns in isolated and connected stream pools: effects of pool volume and spatial position. Oecologia. 1997;110:560–566.
36. Doak DF, Mill SL. A useful role for theory in conservation. Ecology. 1994;75:615–626.