Simultaneous measurements of energy expenditure and weight loss in resting birds allowed determining stoichiometrically total evaporative water loss (TEWL) in non-passerines and passerines. Amount of heat dissipated through water evaporation depends on body size. The dependence of evaporative heat loss on ambient temperatures (T_A) obtained from the energy equivalent in the species studied in this work is the same as that measured with traditional methods. The dependence of water loss on determining body mass at different T_A varies in the same way to the correlation between evaporative and non-evaporative heat loss. In Passeriformes, TEWL is approximately 25–40% higher than in non-passerines (particularly at high T_A), which is consistent with the ratio of their basal metabolic rate (BMR) levels. A high BMR in Passeriformes includes not only net benefits but also its maintenance requires a definite cost. A large expenditure of evaporative water determines the cost of the advantages of BMR increase. This expenditure increased with the body size in Passeriformes due to the forced evaporative heat loss and showed virtually no increase in Non-Passeriformes. The correlation between evaporative and non-evaporative heat loss at different ambient temperatures reflects this cost. A great amount of evaporative water (particularly in large passerine) imposes strong limitations on the range of sizes in Passeriformes.

Keywords: water loss, heat dissipation, evaporation, respiration, thermoregulation, metabolic heat production, energetic equivalent of the loss body mass, birds

Endothermic animals exchange heat with the environment via four modes: conduction, convection, radiation and evaporation). Evaporation is of significant ecological interest. Evaporation from an animal always results in a decrease in the temperature of the surface from which the evaporation occurs. Therefore, evaporation is one-way transfer which causes heat loss from the organism. Biological evaporation always implies loss of water which is a vital resource for nearly all biochemical processes. Evaporation is the loss of heat via the loss of body mass.¹ First guidance for the direct weighing method to determine evaporative water loss was obtained from the studies of Hutchinson and Sykes² and Hutchinson³ on evaporation in domestic fowl. Robert С Lasiewski, Alfredo L Acosta and Marvin H Bernstein using new techniques and equipment, invented new methods different from the original method. A major disadvantage of the direct weighing method is that it does not permit the simultaneous determination of the energetic cost of evaporative cooling by monitoring oxygen consumption or carbon dioxide production, as is possible in the open flow method. As previous studies have shown,^4–7 it is possible to determine evaporative heat loss from the ratio (q) between heat production (RM) (determined by the rate of oxygen consumption) and body mass loss (Dm) at various ambient temperatures (T_A): q=RM/Dm. High water loss necessitates regular water ingestion through drinking, consuming water in food, and metabolic water production. The method is based on the law of conservation of mass where the total mass of the reactants equals the total mass of the products leading to the insight that the relations among quantities of reactants and products typically form a ratio of positive integers (stoichiometry). The method uses the metabolic rate (oxygen consumption) of the bird at thermo neutral ambient temperatures (T_A), respiratory quotient (RQ), the loss of body mass and the energetic equivalent of the loss of body mass (q) as the ratio between heat production and the loss of body mass. It is known that the loss of mass in bird exposed to controlled conditions is due to three major factors:^8–10

1. Gaseous exchange - any excess of the weight of CO₂ produced over the weight of O₂
2. Fecal and urinary loss.
3. Evaporative water loss.

When the metabolic responses of the bird and RQ are known, one can easily account for total evaporative water loss.

Total evaporative water loss (TEWL) at ambient temperature 25°C is summarized in two reviews.^11,12 The chief mechanisms for the transition of minimal to maximal heat loss are a change in plumage position, from ruffled to tightly pressed, the change in blood flow as a result of vasomotor reactions and adaptive rate of evaporation. The following questions are discussed in this paper: (1) How do the TEWL measurements based on the energy equivalent of the body mass loss (q) compare to the TEWL values obtained by the open flow method? Since McNab,^13,14 has convincingly demonstrated that Passeriformes and Non-Passeriformes birds differ in their basal metabolic rate, the subsequent question follows: (2) What is the relationship between TEWL and body mass in Passeriformes and Non-Passeriformes birds at thermo neutral ambient temperatures?

The study was performed in Moscow Region at Zvenigorod Biological Station (55°44′ N, 36°51′ E). More than 60 species of Passerine birds representing the full size range of the order, from the Goldcrest (Regulus regulus, 5.5g) to the Raven (Corvus corax, 1,208g) and 30 species of Non-passerine birds in the corresponding size range (25-4,000g) were chosen for analysis. All birds were kept in large aviaries at natural day lengths and temperatures. For migratory birds and subtropical species, the aviaries were heated in the winter to maintain temperatures of 5-10^oC. These conditions allow accurate studies of seasonal acclimatization.¹⁵ Measurements of energy values were made in the winter (November-January, February) and summer (late May-June, late August - September) on non-molting birds. Studies of seasonal variation in energy expenditure at rest, were done at experimentally controlled temperatures, where T_A was varied from -28^oC to +40^oC in order to construct a thermal energy profile of each of the studied species.

Measurements of body mass variations in birds

Body mass variation is an aggregate of numerous variations, often in opposing directions. The simplest case is the body mass variation of a bird whose alimentary canal had remained empty for several hours. Under such conditions body mass decreases solely because of the water and carbon loss through respiration (in expired carbon dioxide), alimentary canal discharges in the form of mucus and gastroliths, shedding of feathers and variation in plumage moisture. Only the last factor may show an increase of body mass. Plumage which appears dry, contains 150-500 mg moisture in a bird weighing 20g. Loss of body mass at night in such birds amounts to 0.05-0.30g/hr.^16,17

Metabolic rate measurements

To improve the efficiency of determining the level of metabolism, we used three different methods of measurement of oxygen consumption and carbon dioxide exhaled. Oxygen consumption determined using Kalabukhov's closed-loop respirometer system¹⁸ with some modifications,^19,20 in all the birds and at all studied ambient temperatures. The apparatus operates on the following principle: oxygen is consumed by the bird and the expired carbon dioxide is immediately absorbed. The decrease in gas pressure causes oxygen to be drawn from the container into the bird chamber. Then an equal amount of water flows from the burette into the container through the water-type pressure valve to replace the oxygen. Oxygen consumption can be read from the water level in the burette. During the experimental period the pressure inside the respirometer is slightly lower than the atmospheric pressure. A bird was placed in a sealed Plexiglas chamber, which was connected to a ventilation pump. The size of a chamber corresponded with the size of the bird and had 3, 5, 19 or 24L. After 2-3 hours, when the birds are asleep and the temperature has stabilized, the camera connected to the device for the measurement of oxygen consumption. As an absorber dry alkali KOH was used. Cameras were equipped with thermistors, and temperatures temperatures in the camera were monitored remotely by Electronik 16 potentiometric recorder. A camera was placed in thermostat or in refrigerator. For one night measurements were performed for not more than at two temperatures, each after a 2-3 hour of acclimatization. In summer it was possible to do experiment with only one temperature because of short nights. Measurement was performed continuously for 2-4hours, data were recorded every 1 hour. The temperature inside the chambers and in the laboratory were recorded to 0.1°C, atmospheric pressure was 0.5 mmHg, volume of consumed oxygen was 0.2 mL. After MR measurements, birds were weighted to 0.1g, checked for molt stage (the molt score was recorded) and released at dawn in the aviary. Laboratory equipment made it possible to study maximum 18 birds per night.

All the oxygen consumption values were corrected to standard pressure and temperature according to the equations given by Depocas and Hart.²¹ Respirometer in our modification is based on measurements of air pressure and, therefore, the very sensitive to temperature changes. We carefully controlled the temperature in the laboratory during the measurement MR, and in sealed chambers. If the temperature fluctuations in the sealed chamber within one hour of measurements exceeds 0.3^oC the data won’t be used. The average volume of consumed oxygen from the whole time of metabolic rate measurements was transformed into volume at standard temperature and pressure and converted to kJ day^-1 according to the equation 1L of O₂=15.97+5.16RQ (kJ).²²In this manner,the oxygen consumptionwas measuredat restat differentambient temperaturesin allspecies studied.

Measurement of RQ

Respiratory quotient RQ was determined by the gas analyzer of Hаldene. Haldane gas analyzer is designed on the principle of successive absorption of the components of the gas mixture (carbon dioxide is absorbed by alkali and oxygen–by pyrogallol), the volume of residual gas is measured. Samples of air from the sealed chamber in which a bird breathed during 15 minutes were collected into a special bag. The volume of breathed air was measured in a gas meter and samples were analyzed for the O₂ and CO₂ concentrations. A known volume of the gas sample was first treated with KOH solution. CO₂ was taken up by KOH resulting in a corresponding decrease in the original volume of the gas sample being analyzed. From this the concentration of CO₂ in the expired air was found out. Later the remaining gas was made to react with alkaline pyrogallate (pyrogallic acid in KOH) which absorbs O₂; from this the concentration of O₂ in the expired air was known. Because the bird inhaled atmospheric air whose composition was known (practically constant) it was easy to find out the amount of O₂ used and CO₂ given off in the experiment. From these values RQ is calculated by the formula, RQ =Volume of CO₂ exhaled/Volume of O₂ utilized. AJS Benadé et al.²³ were carried out experiments, in which oxygen content, carbon dioxide content and RQ's obtained on expired air samples by the Haldane technique, were compared with those obtained by means of paramagnetic and infrared analysis. No significant bias was found between Haldane and paramagnetic analysis of oxygen content. Infrared analysis yielded more consistent results for CO₂ than did the Haldane apparatus. RQ.'s calculated from the chemical and physical methods were almost identical. Physical methods, when properly used and frequently calibrated, can be regarded as being just as accurate as the accepted standard chemical method.²³

In this way, we measured the energy expenditure at rest and respiratory quotient in 26 species of passerine birds and 16 species of non-passerine birds in the winter and summer (publications mainly in Russian, but there are some in English.^5,6,24 Measurements were made at different temperatures in the range from+5 to+35°C. In the third series of measurements we determined oxygen consumption and carbonic gas exhalation in the birds using a flow-through respirometer Fox Box of Sable Systems Inc. Simultaneously the rate of air passage through the chamber, temperature in the chamber, and the concentration of carbonic gas and oxygen were recorded. The intensity of ventilation of the respirometer chamber (passage rate) was set within 600–850 mL/min. Through the hermetic respiration chamber in which the bird was located, air was blown in an incessant flow. The rate of oxygen consumption and carbonic gas exhalation was calculated on the basis of measuring the difference between the concentration of these gases at the output of the respiration chamber with the bird and at the output of an empty similar chamber, multiplied by the rate of air passage through the chamber. The concentration of carbonic gas and oxygen after respiration chamber with the bird and a similar empty chamber was measured successively in one device during 24–30 and 6–10min, respectively. The frequency of taking device readings was once per 10s. Measurements were performed in the night in a darkened chamber at a different ambient temperature. Measurements started at 1-2hours after the birds fell asleep and the chamber temperature has stabilized. The respiratory quotient was determined during these experiments. Energy metabolism in birds was calculated incessantly on the basis of the calculated values of the respiratory quotient at the given moment of time. This series of experiments is in the very beginning, at the moment measured only 35 species, the results concerning one of these species was published.²⁵

The stoichiometric approach in calculating of total evaporative water loss

Simultaneous determination of the energy expended and mass loss in resting birds was used to estimate the energetic equivalent of body mass loss (q). During the measurements of q, the birds were in the post-absorptive state, and because measurements were performed during the non-breeding, non-molting, non-migrating seasons of the year, no production (growth or reproduction) occurred during these measurements. The birds did not have drinking water, and they metabolized previously ingested food. I performed preliminary experiments to determine the time of a day (in 24-hour cycle) when the loss of body mass of the bird was minimal and bird’s rate of metabolism was constant. Our data for some species were consistent with the results of previous experiments,^4-7,17,26 and suggests that mass losses resulting from cloacal excretions and products of nitrogen metabolism remain very small under these experimental conditions and may be ignored. Therefore, the main variable affecting the q value is the pulmonary and cutaneous evaporation of water. This interrelationship is expressed as follows:

$q=C_{s}DW/Dm\infty$ (1),

Where C_s is the energetic content (kJ/g) of the oxidized ingredient (fat=39.7 kJ/g; carbohydrate= 17.6 kJ/g; protein=18.4 kJ/g), DW is the mass of food oxidized during energy metabolism (in further calculations DW=1 g), and Dm is the loss of body mass comprising the following components:

$Dm=\left(C_{s}W\%H_e\right)/\left(2.4*100\right)+cloacaedischarge+D\left(C{O}_2-O_2\right)$ (2),

where C_s W/2.4*100 is the amount of water (g) necessary for the evaporative removal of 1% heat generated through the oxidation of W g compound of known energetic content (C_s), %H_e is the evaporative heat loss expressed as a percentage of total heat produced during the oxidation of any amount of this compound in the organism, cloacae discharge is the loss of body mass as excreted urine and feces, and D(CO₂-O₂) is the difference in body mass gained from the oxygen consumed and the mass lost from the CO₂ released. The q value, representing the energy equivalent of body mass lost, is related to the level of respiratory evaporation. For example, at higher ambient temperatures, evaporation rapidly increases relative to the metabolic rate observed when birds pant. The relationship between the energy equivalent and the level of evaporation is readily quantified.^16,19,20

During the oxidation of 1 g of fat, the mass of oxygen consumed is 0.07 g greater than the mass of carbon dioxide released, which yielded 1.07g of metabolic (oxidation) water, and also produced 39.7kJ of heat. Therefore, if evaporation is absent, the bird gains 0.07g for each gram of fat that it oxidized as a result of this metabolic water. The heat of vaporization of water is 2.4kJ/g. If a portion of the heat produced during metabolism was lost via evaporation, the loss of body mass (Dm) per 1 g of the oxidized substrate (fat) resulting from evaporative heat loss (H_e) is as follows:

where %H_e is the percent of total produced heat loss through evaporation. Considering the constant addition of mass resulting from excess metabolic water, which, with respect to loss of body mass, is a negative value, q is dependent on the proportion of body heat production lost via evaporation at rest during the oxidation of fat, determined as shown below:

$q=39.7/\left(39.7/\left(2.4*100\right)\right)\%H_e-0.07=39.7/0.164\%H_e-0.07$ (3)

There are two unknown variables in this equation: q and %H_e; however, q is an experimentally determined value obtained at different ambient temperatures. It is possible to find %H_e as follows:

$\%H_e=\left(39.7/q+0.07\right)/0.164$ (4)

Upon the oxidation of 1 g of carbohydrate, 17.6 kJ of heat is released and 0.56g of metabolic water is produced, and because the mass of released carbon dioxide is 0.44g more than the mass of consumed oxygen, this variable is not associated with the loss of body mass through evaporation. Correspondingly, the dependence of body mass loss and q on the level of evaporative heat loss during carbohydrate oxidation is represented as

$q=17.6/Dm=17.6/\left(0.072*\%H_e+0.44\right)$ (5)

The oxidation of 1g of protein yields 18.4kJ of heat, 0.49g of metabolic water and 0.47g of nitrogen metabolism products. The weight of released CO₂ is 0.04 g more than the consumed oxygen, this is because during prolonged experiments, nitrogen metabolism products are excreted, the loss of body mass at %H_e=0 is 0.47 g+0.04 g = 0.51 g per 1 g of oxidized protein as follows:

$q=18.4/Dm=18.4/\left(0.076*\%H_e+0.51\right)$ (6)

Equations (4), (5) and (6) can be transformed into an exponential form. For metabolism of fat, equation (4) is represented as

$\%H_e=238.3q^{-0.98}$ , where q is in kJ/g or $\%H_e=2.76q^{-0.98}$ , q where q is in W/g (7)

Equation (7) facilitates the calculation of %H_e for specific q values for fat metabolism, determined during the winter. Evaporative heat loss for any combination of oxidized compounds can be calculated using this method. Our early work,^26,27 based on the change of the diurnal variations of body composition in finches and house sparrows during the annual cycle, suggested that during the summer period the ratio of oxidizable substrates at night was close to 0.7 for fat, 0.2 for carbohydrates and 0.1 for proteins. With such ratio of oxidizable substrates RQ must be equal to $0.7*0.7+0.2*1+0.1*0.82=0.77$ .

A combination of oxidized substrates in the bird species during the summer, including fats, carbohydrates and proteins at 0.7:0.1:0.2, respectively, was used. The total q comprises 0.7q for fats, 0.1q for carbohydrates and 0.2 q for protein, represented as

$\begin{array}{l}q=0.7*39.7/\left(0.164*\%H_e-0.07\right)+0.1*17.6/\left(0.072*\%H_e+0.44\right)+0.2*8.4/\left(0.076*\%H_e+0.51\right)\\ 0.7*0.7+0.2*1+0.1*0.82=0.77\end{array}$ (8)

For the exponential form, this equation is represented as

$\%H_e=239.3q^{-1.05}$ , $whereq=kJ/gor\%H_e=2.77q^{-1.05},q=W/g$ (9)

The regressions (7) and (9) were fitted using the least-squares method of linear regression.

Because the evaporative heat of 1 gram of water is equal to 2.4 kJ,²⁸ total evaporative water loss is represented as

$TEWL=\left(BMR*\%H_e/100\right)/2.4$ ,

Where BMR is the total heat produced at any thermo neutral T_A, and %H_e is the percent of total heat lost through evaporation at this T_A. Therefore, a definite correlation between the energy equivalent and total evaporative water loss for any ambient temperature was observed.

Scaling analysis and statistic

Calculations and statistical processing of the results were performed using the Statgraphics program package. All data are expressed as the means±SD. The figures (including curve fits and correlation coefficients) were produced using Harvard Graphic 3.0 software. Linear curve fits are plotted in figures, and the lines for He and %He are polynomial curve fits. The relationships in the present study were estimated using analysis of variance (ANOVA), and significance was determined using the t-test, as appropriate. The following statistics-associated abbreviations were used in this manuscript: n, sample size; p, statistical significance; t-test for independent samples: Variables for S and W were treated as independent samples r, Pearson’s linear correlation; SD, standard deviation. We used the data for scaling analysis of total evaporative water loss in Passeriformes and Non-Passeriformes birds at different ambient temperatures. First question concerning the relationship between TEWL and body mass by collating data on TEWL at different ambient temperatures (25°C and real low critical temperature (T_lc) and upper critical temperature (T_uc). T_lc and T_uc are ecologically significant ambient temperatures; reasons for selecting data taken at 25°C were that this temperature is: (1) at or near the lower critical temperature for many birds; (2) thermally unstressful for most birds; and (3) consistent with that chosen by Crawford and Lasiewski¹¹ and Williams¹² for their analysis.

We used the statistics package R(R Development Core Team. 2014. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing) for log-transformed values of TEWL (g H₂O/day) and body mass (g) (Figure 3). At first, we was preparing a table with three columns. In the first - log mass, the second-log og-transformed values of TEWL in the third-the code for the group (for example, 1 - Passeriformes, 2–Non-Passeriformes).To test differences in the slope of the regression, we tested using SuperANOVA difference between the model with the interaction of mass and group variable and the model without this interaction. To test differences in the intercept, we tested using SuperANOVA difference between the model without interaction of factors. For computational convenience the homemade program written in Matlab^® was used for statistical analysis of the data. The program was tested against SuperANOVA and produced identical results. The study was performed in accordance with the laws of the Russian Federation and Moscow State University regarding the capturing and holding of wild animals and all individuals were released after the experiment.

Body mass loss after feeding

The decrease of birds' mass subsequently proceeded in smaller birds’ at a constant rate during 2-4 h after the last feeding, and in larger birds–at a constant rate after 10-12 h (Figure 1). Based on our experiments, we considered that 2 hours after the last feeding in small birds and after 10-12h in large ones the birds' alimentary canal becomes empty. Rate of body mass loss (see Methods) after evening feeding stabilizes at different times in birds of different sizes: on average, it occurred after 2-4h in small birds and 6-8 h in large birds and further loss at constant rates determined by water evaporation. Figure 2 exemplifies this trend showing that the alimentary canal became empty after 5h in Carolina ducks (body mass 470 g) and 3 h in Chaffinches, Budgerigar and Green Finch (body mass 21, 28, 28 g respectively). Consequently, all birds fasted for at least 3 -12h and were in postabsorptive state during measurements. Therefore, we believe that body mass loss occurs during the measurement with the same rate.

Figure 1 Body mass loss per hour as a function of time after feeding for small (upper panel) and large (bottom panel) birds. Data for upper panel were slightly displaced horizontally to prevent overlapping. Body mass was measured every hour and thus body mass loss per hour is a mass difference between two successive measurements.

Figure 2 Top. total evaporative water loss (TEWL, g per day; vertical bars are SE, right scales) and percentage of heat loss through evaporation (He, %, left scales) as the functions of ambient temperature (TA, oC) in the Chaffinch, Fringilla coelebs in summer (left) and winter (right).
Bottom. energy expenditure at rest (SMR, BMR, kJ per day) evaporative heat loss (He, kJ per day), non-evaporative heat loss (Hs, kJ per day) as the functions of ambient temperature (TA, oC) and changes in the energy equivalent of lost body mass (q, kJ per g). Each symbol is a mean for several measurements in several birds at a given TA, vertical bars are SE.

Figure 3 total evaporative water loss (TEWL) and evaporative heat loss at T_A= 25oC as a function of body mass (m, g) in all birds (this study and Willams, 1996).

Results of measurement of RQ and a comparison of different methods for measuring RQ

RQ values in 26 species of passerine birds and 16 species of non-passerine birds obtained by the Haldane gas analyzer at night in winter at ambient temperatures of 5-35^oC was in the range 0.69-0.75 and on average equal to 0.72±0.03 (n=1024). RQ values in 5 species of passerine birds obtained by the Fox Box respirometer o(Sable Systems Inc) at night in winter at ambient temperatures of 15-30^oC was in the range of 0.71-0.76 and on average equal to 0.73±0.03 (n=38). These data indicate that lipids were the main source of energy expenditure in winter during night. RQ values in 26 species of passerine birds and 16 species of non-passerine birds at night in summer at ambient temperatures of 5-35^oC was 0.74-0.79 on average 0.77±0.03 (n=1024). RQ values in 33 species of passerine birds obtained by the Fox Box respirometer (Sable Systems Inc) at night in summer at ambient temperatures of 15-30^oC was in the range of 0.71-0.82 and on average equal to 0.765±0.039 (n=292).

The mean difference between the Haldane and Kalabuchov respirometer determinations was – 0.071% O₂, with a standard error 0.011% (n=1024). The mean difference between the Haldane and Fox Box respirometer (Sable Systems Inc) was 0.08% RQ with a standard error of 0.012% (n=232). Thus, RQ's and metabolic rate determined by different methods were almost identical. The average values ​​of metabolic rate and of RQ obtained by different methods were used for further computations. To test more accurate RQ values, we determined RQ two ways using only the same species. We did not found any difference in determining the RQ by these two methods n=324 (Table 1). These data indicate that lipids were the main source of energy expenditure in winter during a night – RQ=0.72, and RQ=0.77 in summer. Such RQs can be at any ratio of oxidizable substrates: lipids, carbohydrates and protein. Our early work based on the change of the diurnal variations of body composition in finches and house sparrows during the annual cycle, suggested that during the summer period the ratio of oxidizable substrates at night was close to 0.7 for fat, 0.2 for carbohydrates and 0.1 for proteins. With such ratio of oxidizable substrates RQ must be equal to .

The average volume of consumed oxygen from the whole time of metabolic rate measurement was converted into the volume at standard temperature and pressure and then converted to kJ day according to the equation: 1L of O₂=15.97+5.16RQ (kJ),²² and then used as an estimate of the whole-organism metabolic rate. For comparison of different methods for measuring metabolic rate, we additionally considered here another common metabolic measurements–mass-specific metabolic rate (in kJ day-1*g) and mass-independent metabolic rate (residuals from regression of log metabolic rate on log body mass).

Data of metabolic rate, energetic equivalent of the loss body mass, lower and upper critical temperatures, total evaporative water loss

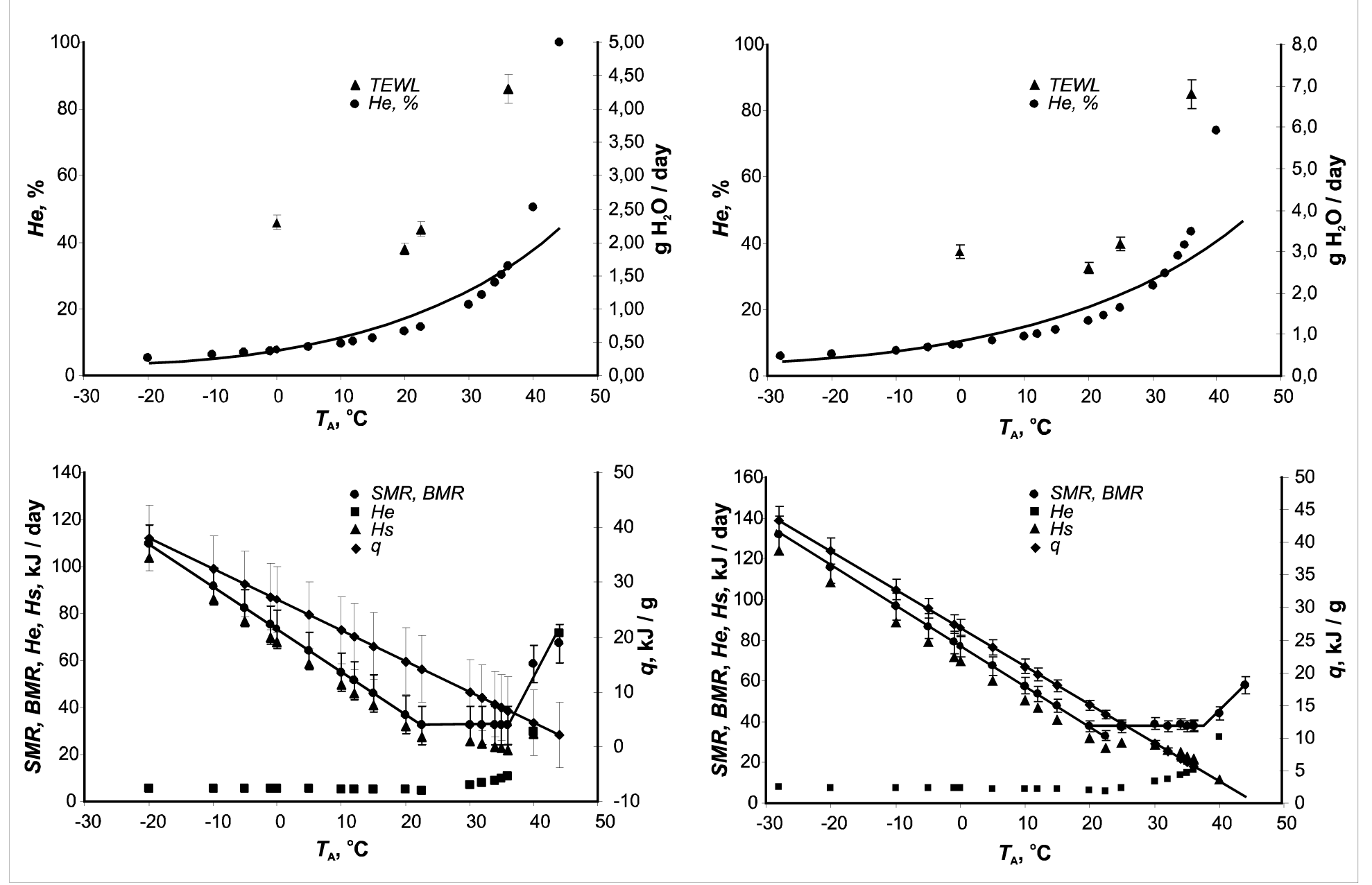
All of the obtained data on heat loss at rest (BMR) and the associated values measured (q, H_e, and TEWL) for all bird species for two seasons are summarized in (Table 2). Most of the BMRs measurements results have been published in reviews,^6–8,17,27 and entered into the critical analysis of Makarieva et al., 2008,²⁹ McNab.¹³ As an example, the obtained values of energy metabolism in summer for one of the passerine species, the Chaffinch (Fringilla coelebs), are also presented in graphic. The data indicate that evaporation was minimal at T_A=T_1с, and the rate of evaporation increased at lower or higher temperatures. The rate of evaporation only slightly increased at T_A<T_1с, when the role of evaporative heat loss in the heat balance decreased. The dependence of evaporative heat loss on T_A obtained from the energy equivalent in the species studied in this work is the same as that measured in known specimens with traditional methods.

Allometric analysis

In his study, Williams (Williams 1996) selected data taken at 25^oC because this temperature is (1) at or near the lower critical temperature for many birds, (2) thermally not stressful for most birds, and (3) consistent with that chosen by Crawford and Lasiewski (1968) for their analysis.

Evaporative water loss of/for the entire Aves (based on combined data from this and Williams’ studies)

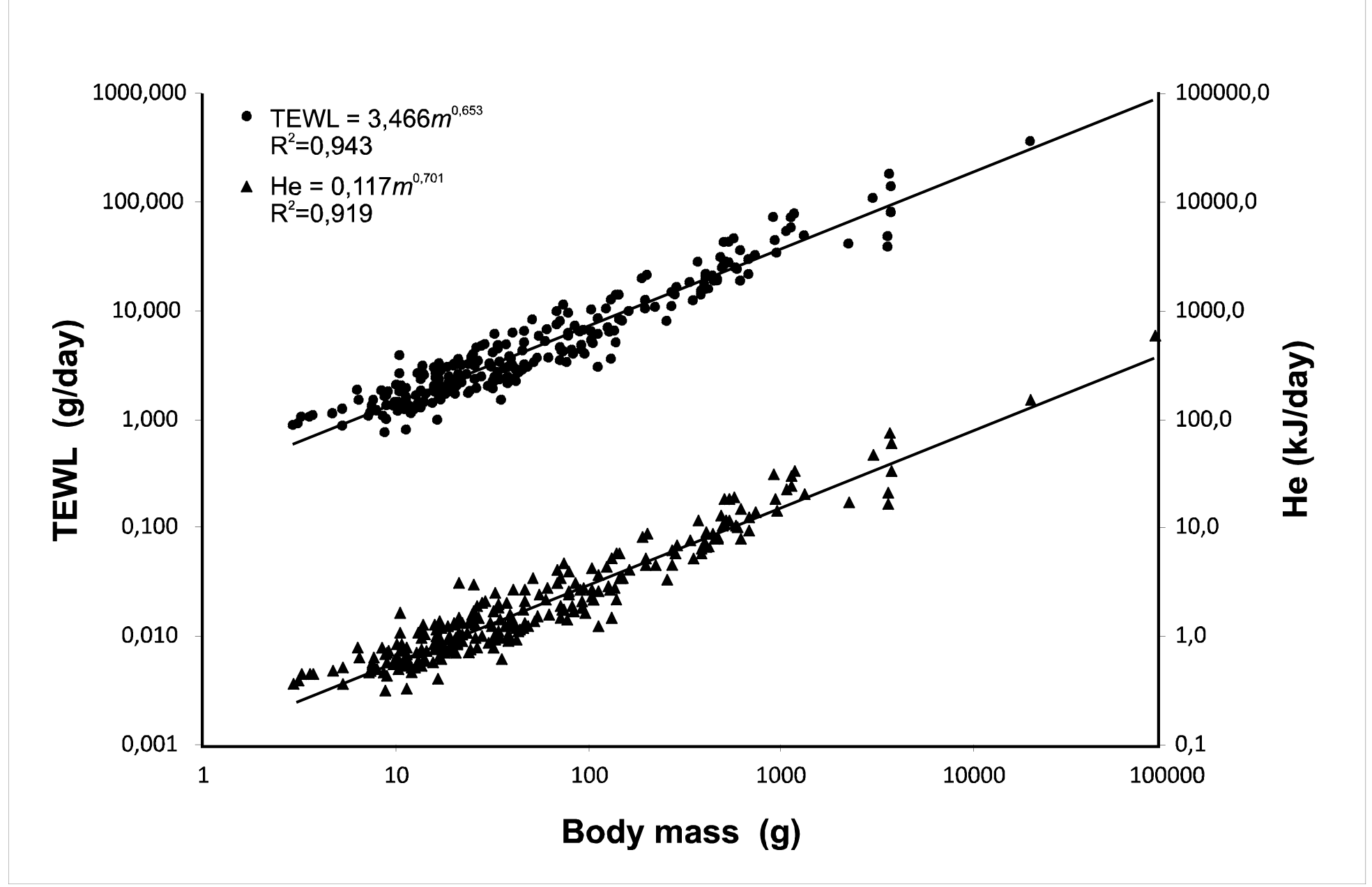
After combining the data for 102 species of birds from obtained by Williams¹² and our data for 157 species of birds at thermally neutral temperatures (mostly 25^oC) to improve the statistical significance, the relationship between TEWL and body mass is: TEWL25^oC Aves = 0.28 m^0.70, R² = 0.92, where TEWL is expressed as g H₂O/day and m is body mass (g). Comparison of our data for TEWL, obtained through measurement of the energy equivalent of the body mass loss (q) and calculated for the same temperature (25°C), with the results obtained by traditional methods (Williams 1996) revealed good agreement between the two methods: TEWL25°C Williams, all= 0.29 m^0.68, R²=0.90; TEWL25^oC This study, all=0.27 m^0.71, R²=0.93. The differences are not significant. (The difference in slope is ns F=1.4578, p=0.2284; the difference in the y-intercepts is ns F=0.8987, p=0.344).

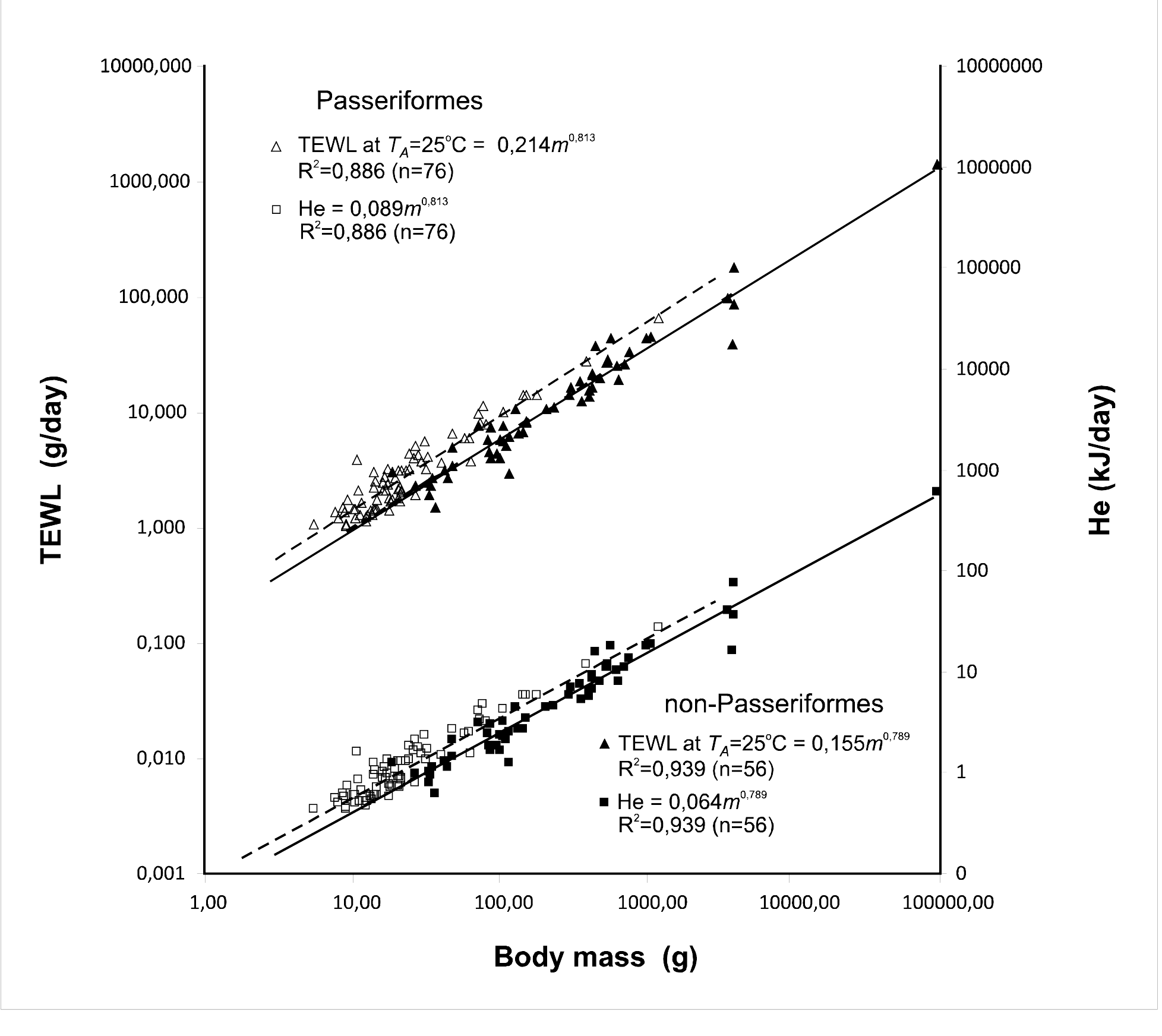
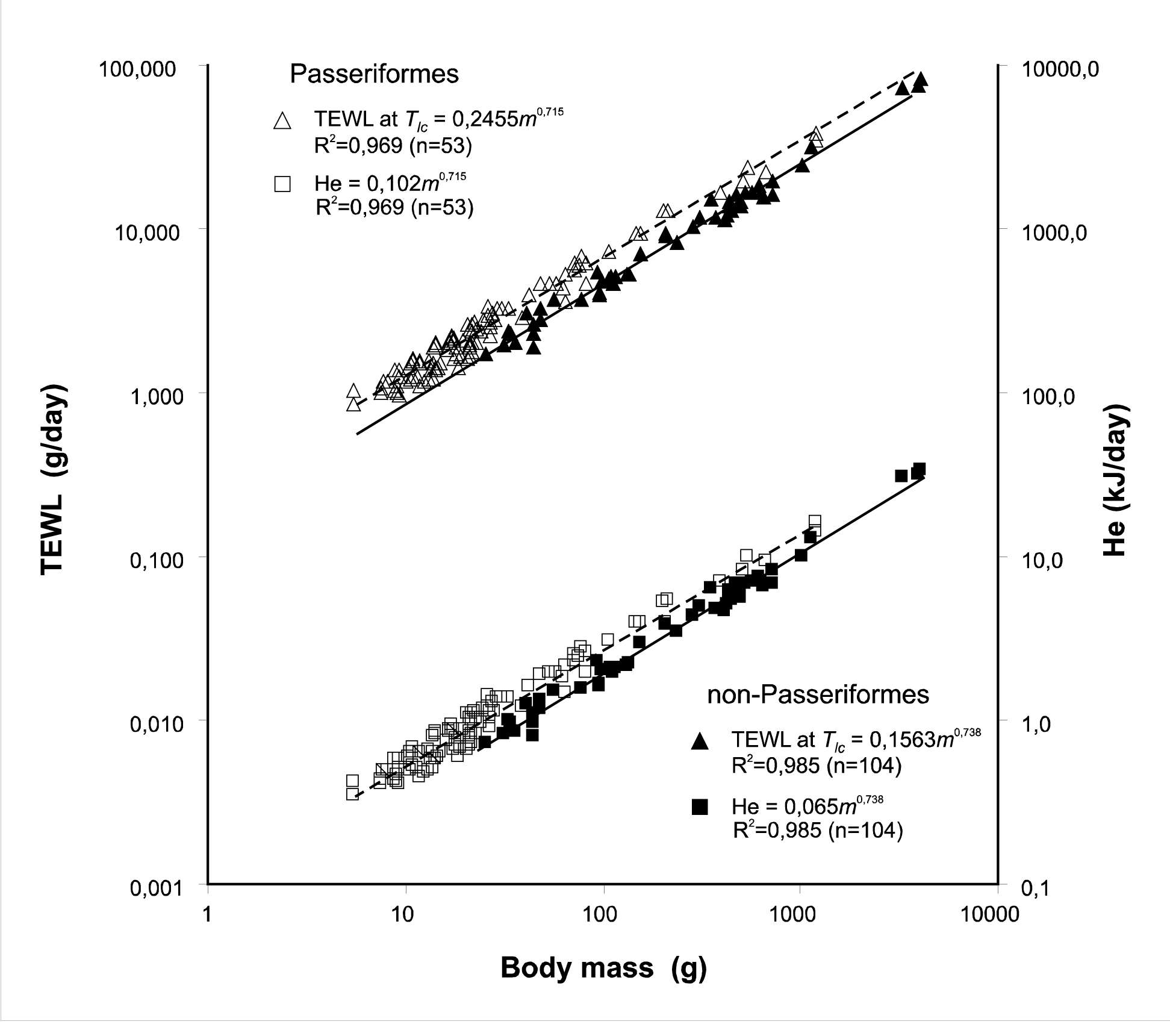
Because the evaporative heat of 1 gram of water is equal to 2.4 kJ,²⁸ we calculated total heat loss by evaporation (H_e) as TEWL/2.4 (Figure 4). In the next figures we include H_e along with TEWL. Since McNab,^13,14 has convincingly demonstrated that Passeriformes and Non-Passeriformes birds differ in their basal metabolic rate. We analyzed the water loss separately for these groups. Our data allow calculation of the allometric relationships for three different thermo neutral ambient temperatures and separately for passerines and non-passerine birds (Figures 5-7). The statistical significance of each pair of equations as the slope and y-intercept for Passeriformes and Non-Passeriformes. Only at T_A=25°C do the equations differ in both the slope and y-intercept. The relationship between TEWL and body mass shows that the ratio of TEWL to body mass in passerine birds is higher than in Non-passerine birds’ at all ambient temperatures (T_lc, 25°C, and T_uc). Evaporative heat loss (H_e) dissipates 10-16% of heat at 0^oC,(Figure 8) 16.2-20% at T_lc and 40-65% at T_uc. At low T_A, the role of heat loss through evaporation is low, and virtually all of the energy used in thermoregulation is expended through conduction, convection and radiation. Evaporative heat loss increases significantly in the thermo neutral zone, even though the birds increase thermal conductance. Evaporation accounted for 100% of the heat loss at T_A > T_uc. The contribution of H_e to total heat loss increased more than 6-fold with a temperature increase from 0°C to T_uc, whereas the amount of evaporated water (TEWL) increased no more than three times.

Figure 4 Total evaporative water loss (TEWL, gH₂0 per day, the left ordinate ) and evaporative heat loss (H_e, kJ per day, the right ordinate) at T_A=25oC as a function of body mass (m, g) in all birds.

Figure 5 Total evaporative water loss (TEWL, gH₂0 per day, the left ordinate ) and evaporative heat loss (He, kJ per day, the right ordinate)at T_A=25^oC as a function of body mass (m, g) in Passeriformes and Non-Passeriformes.

Figure 6 Total evaporative water loss (TEWL, gH₂0 per day, the left ordinate ) and evaporative heat loss (H_e, kJ per day, the right ordinate)at T_A=Tlc as a function of body mass (m, g) in Passeriformes and Non-Passeriformes.

Figure 7 Total evaporative water loss (TEWL, gH₂0 per day, the left ordinate ) and evaporative heat loss (H_e, kJ per day, the right ordinate) at T_A=Tuc as a function of body mass (m, g) in Passeriformes and Non-Passeriformes.

Figure 8 Total evaporative water loss (TEWL, gH₂0 per day, the left ordinate ) and evaporative heat loss (H_e, kJ per day, the right ordinate)at T_A=0oC as a function of body mass (m, g) in Passeriformes and Non-Passeriformes.

This paper presents the stoichiometric approach to calculation of total evaporative water loss and relationship between evaporative and non-evaporative heat loss in Passeriformes and Non- Passeriformes birds. The total evaporative water loss constitutes a part of the heat balance of the animal, especially large and important in warm conditions.^30–43 Several studies have shown that the rates of evaporative heat loss can exceed the energetic metabolic rates.^10,44–49 The rate of heat dissipation proportional to the total evaporative water loss (TEWL) is strongly influenced by both acclimatization and, presumably, natural selection, and thus varies among species.⁵⁰ It is assumed that TEWL relates to the metabolic rate.^51,52 The body mass loss of a bird in the post-absorptive stage at а constant relative humidity is primarily determined by water evaporation. A major advantage of this method for determining TEWL at low ambient temperatures is that condensation or freezing of water vapor does not affect measurement accuracy, as is the case for measurements of humidity, dew point, or water vapor pressure.

The analysis suggests that the slope of the Williams (1996) equation, 0.68, should fit the relationship between TEWL and the body mass for birds in Williams study (n=102) at T_A=25^oC. A slope of 0.70 was found for all birds–both Williams’ and this study (n=102+157=259) at T_A=25^oC. Separation of the data into groups (Passeriformes and Non-Passeriformes) increases the slopes of the equations. There are differences between Passeriformes and Non-Passeriformes at T_A=25^oC, T_A=0^oC, T_A= T_lc, and T_A= T_uc. At T_A=25^oC, the differences are in both the slope and intercepts. The basal metabolic rate (BMR) and the total evaporative water loss (TEWL) are believed to have occurred in conjunction with life-history traits often assumed to be characteristics of the animal. As we believe that non-passerine birds and passerines have different levels of basal metabolic rate, we give a lot of attention to the TEWL in the thermoneutral zone. Allometric equations were derived for the dependence of the total evaporative water loss (TEWL, g/day) on the body mass at various T_A (0°C, T_lc, and T_uc) for winter and summer in Passerine and Non-passerine birds. The dependencies were analyzed with respect to the differences in the BMR levels of these two groups according McNab’s publications (2009, 2016). The dependences of the evaporative water loss on the body mass at various T_A (0°C, T_lc, and T_uc) were different, as were the ratios between evaporative and non-evaporative heat dissipation. Only at T_1с did the evaporative water loss increase in parallel with the metabolic rate: at T_uc, large-bodied birds dissipated more heat by evaporation than small birds. The slopes of the regression lines for TEWL increased for both Passerine and Non-passerine birds, reflecting increasing difficulties in main­taining heat balance in large-bodied birds at high T_A. The total evaporative water loss at ambient temperature (25^oC) was summarized in two oft-quoted reports. This equation gives similar values of evaporative water losses to those determined by the above-described and conventional methods.

The percentage of heat dissipated by water evaporation also depends on the body size. At T_lc, it was equal to 17-18% in birds of various sizes. Experiments showed that the evaporative heat loss accounts for approximately 40-60% of the heat produced by BMR at T_A=T_uc; this fraction increased with the body size (m^0.007) in Passerines and showed virtually no increase in Non-passerines. The water loss increased with body size (m^0.17) in Passerines because of forced evaporative heat loss. In Non-passerine birds, there were nearly equal increases in the evaporative water loss and metabolic rate: m^0.73 in the summer and m^0.69 in the winter, suggesting that this group maintained the heat balance even at T_uc.

At 0°C and T_lс, the lines describing the effects of the evaporative and non-evaporative heat losses on the body mass do not intersect in the range of real sizes; however, at T_uc, the lines of regression for H_e and H_s intersect at a body mass of approximately 25g in Passeriformes.^6–8 These facts show that relatively larger passerine birds at high ambient temperatures find it more difficult to maintain their heat balance. These birds must use additional water evaporation to maintain their heat balance. A high BMR level includes not only with advantages to have higher productive energy and to breed at lower ambient temperatures but its maintenance also requires a definite cost. A large expenditure of evaporative water determines the cost. This expenditure increased with the body size in Passeriformes due to the forced evaporative heat loss and showed virtually no increase in Non-Passeriformes. This dependence at T_A equal to 0°C, T_lc, and T_uc varies in the same way as the relationship between evaporative and non-evaporative heat loss.^6-8 The total amount of water evaporated in the neutral thermal zone (at T_lc or T_uc) was considerably greater in Passerines than in Non-passerines (by approximately 40%). This is in agreement with differences in the levels of BMR at T_lc between the two groups.^13,14 Thus, a large expenditure of evaporative water reflects the cost of the advantages of BMR increase and results in a higher energetic capability.

Evaporation is a necessary attribute of the conservation of heat balance, but it is largely derived from the metabolic rate, ambient temperature and relative humidity. Evaporation is caused by different gradients of water absorption at various temperatures and the difference between the density of the saturating vapor and the actual density of vapor fed into the system from the surfaces of respiratory organs and skin (the experiments were performed at а constant relative humidity, and we did not use dried air, which would stimulate evaporation). The basal metabolic rate and non-evaporative thermal conductance are fundamental parameters of energetics and determine the level of physiological organization. BMR and ‘dry’ thermal conductance are dependent on the architecture of the circulatory and respiratory systems and on plumage insulation. Non-evaporative thermal conductance is more of an order characteristic because it is the thermal conduction that reflects the architectonics of the circulatory system and the abilities of the vasomotor reactions. Thus, h_l and BMR are integrated parameters of the functioning of the systems associated with the assimilation of oxygen and maintaining constant body temperature.

These findings suggest that the high level of basal metabolism in Passeriformes in comparison to Non-Passeriformes determines the necessity for them to utilize con­siderably greater amounts of water for evaporation to maintain a sufficient heat balance at high ambi­ent temperatures. This requirement imposes strong limitations on the range of body sizes in this group, and despite the consider­able ecological and energy advantages (high maximal existence metabolic rate, MPE and an ability to breed at low ambient temperatures) of such high BMR levels, this pattern is not often found in other groups of endothermic animals. A considerable evaporative water loss reflects the cost of the higher BMR and energy capacities of Passerines in comparison with Non-passerines and other orders of endothermic animals. As shown in the previous study,^7,8 an increase in BMR results in an increase in the maximal existence metabolic rate and potential productive energy, which expands the ecological capability. These energetic changes in Passeriformes confer many benefits but minimize the optimal sizes. Analysis of the allometric regressions for the energetic parameters shows that Passerines with a body mass ranging from 5–150 g have significantly higher productive energy than Non-Passeriformes.^7,8 About 80% of Passeriformes species have body mass in this range. Thus, a large expenditure of evaporative water is the costs of the higher BMR in Passeriformes than in Non-Passeriformes and result in a higher productive energy.⁵³

We are grateful to the researchers of the Department of Vertebrate Zoology and its head, L. P. Korzun, for the opportunity to perform research and for assistance and helpful discussions. I would like to thank A. I. Shilov for help with the drawings and A. V. Bushuev for assistance with the statistical calculations. I would also like to thank the Russian Foundation for Basic Research for long-term support of my research. I thank T. B. Golubeva for support and patient and perceptive help with my studies.

Author declares that there is no conflicts of interest.

1. Porter WP, Gates DM. Thermodynamic Equilibria of Animals with Environment. Ecological Monographs. 1969;39(3):227‒244.
2. Hutchinson JCD, Sykes AH. Physiological acclimatization of fowls to a hot humid environment. J agric Sci. 1953;43(2):294‒322.
3. Hutchinson JCD. Evaporative cooling in fowls. J agric Sci. 1955;45(1):48‒59.
4. Gavrilov VM. Evaporative water loss in the class of birds: method of measurement and allometric dependencies at various ambient temperatures in passerine and nonpasserine birds. Doklady Biological Sciences. 1995;345:621–626.
5. Gavrilov VM. Energetics and Avian Behavior. Soviet Scientific Reviews Series, Section F: Physiology and General Biology. Volume 11. London: Harwood; 1997.
6. Gavrilov VM. Ecological and scaling analysis of the energy expenditure of rest, activity, flight, and evaporative water loss in Passeriformes and Non-Passeriformes in relation to seasonal migrations and to the occupation of boreal stations in high and moderate latitudes. Q Rev Biol. 2014;89:(2):25–69.
7. Gavrilov VM. 2015.The stoichiometric approach in determining total evaporative water loss and the relationship between evaporative and non-evaporative heat loss in two resting bird species: passerine and non-passerine. Avian research. 2015;6:19.
8. Lasiewski RC, Acosta AL, Bernstein MH. Evaporative water loss in birds. II – A modified method for determination by direct weighing. Comp Biochem Physiol. 1966;19(2):459‒470.
9. Lasiewski RC, Acosta AL, Bernstein MH. Evaporative water loss in birds. I. Characteristics of the open flow method of determination and their relation to estimates of thermoregulatory ability. Comp Biochem Physiol. 1966;19(2):445‒457.
10. Dawson WR. Evaporative losses of water by birds. Comp Biochem Physiol A Comp Physiol. 1982;71(4):495–509.
11. Crawford EC, Jr Lasiewski RC. Oxygen consumption and respiratory evaporation of the Emu and Rhea. Condor. 1968;70(4):333‒339.
12. Williams JB. A phylogenetic perspective of evaporative water loss in birds. The Auk. 1996;113(2):457‒472.
13. McNab BK. Ecological factors affect the level and scaling of avian BMR. Comp Biochem Physiol A Mol Integr Physiol. 2009;152(1):22–45.
14. McNab BK. Avian energetics: The passerine/non-passerine dichotomy. Comp Biochem Physiol A Mol Integr Physiol. 2016;191:152‒155.
15. Prosser CL. Comparative Animal Physiology. Philadelphia: WB Saunders; 1991.
16. Dolnik VR, Gavrilov VM. Caloric equivalent of body weight variations in chaffinch Pages 273–287 in Bird Migration: Ecological and Physiological Factors. Bykhovskii BE editor. New York: Wiley;1973.
17. Kendeigh SC, Dolnik VR, Gavrilov VM. Granivorous Birds in Ecosystems: Their Evolution, Populations, Energetics, Adaptations, Impact and Control. Avian energetic. Pinowski J, Kendeigh SC editors. Cambridge: Cambridge University Press. 1977;127–378.
18. Górecki A. Kalabukhov-Skvortsov respirometer and resting metabolic rate measurement. In Methods for ecological energetics. IBP Handbook No. 24: 309–313. Grodzinski, W, Klekowski RZ, Duncan A, editors. Oxford: Blackwell Scientific; 1975.
19. Gavrilov VM. Bioenergetics of large Passeriformes 1. Metabolism ofrest and energy of existence. Zool Zh. 1979a;58:530‒541.
20. Gavrilov VM. Bioenergetics of large Passeriformes. 2. Calorific value of weight, evaporative heat loss and dependence of bioenergetical parameters on body weight. Zool Zh. 1979;58(5):693‒704.
21. Depocas F, Hart JS. Use of the Pauling oxygen analyzer for measurement of animals in open circuit systems and in a short-lag, closed-circuit apparatus. J App Physiol. 1957;10(3):338‒392.
22. Schmidt-Nielsen K. Animal physiology: adaptation and environment. 5th ed. New York: Cambridge University Press. 1997.
23. Benadé AJS, Steydom NB, van der Walt WH. A comparison of physical and chemical methods for the determination of respiratory quotient. Int Z Angew Physiol. 1970;28(3):193‒196.
24. Dolnik VR, Gavrilov VM. Bioenergetics of molt in the chaffinch (Fringilla coelebs). The Auk. 1979;96(2):253‒264.
25. Gavrilov VV, Veselovskaya EO, Gavrilov VM, et al. Diurnal Rhythms of Locomotor Activity, Changes in Body Mass and Fat Reserves, Standard Metabolic Rate, and Respiratory Quotient in the Free-Living Coal Tit (Parus ater) in the Autumn–Winter Period. Biology Bulletin. 2013;40(8):678–683.
26. Dolnik VR, Gavrilov VM. A comparison of the seasonal and daily variations of bioenergetics, locomotor activities and major body composition in the sedentary house sparrow (Passer d. domesticus L.) and the migratory "Indian" sparrow (P.d. bactrianus Zar. et Kudash)), Ecologia Polska (Ecol.pol.). 1975;23:211‒226.
27. Gavrilov VM, Dolnik VR. Basal metabolic rate, thermoregulation and existence energy in birds: world data. Acta XVIII Congress Internationalis Ornithologici. 1985;1:421–466.
28. Garai J. Physical model for vaporization. Fluid Phase Equilibria. 2009;283(1-2):89–92.
29. Makarieva AM, Gorshkov VG, Bai-Lian L, et al. Mean mass-specific metabolic rates are strikingly similar across life's major domains: evidence for life's metabolic optimum. Proc Natl Acad Sci U S A. 2008;105(44):16994–16999.
30. Bernstein MH. Cutaneous and respiratory evaporation in the painted quail, Excalfactoria chinensis, during ontogeny of thermoregulation. Comp Biochem Physiol A Comp Physiol. 1971;38(3);611‒617.
31. Lasiewski RC. Respiratory function in birds. Avian Biology. In: Farner DS, King JR, editors. New York: Academic Press. 1972;287–342.
32. Lee P, Schmidt-Nielson K. Respiratory and cutaneous evaporation in the zebra finch: effect on water balance. Am J Physiol. 1971;220(6):1598‒1605.
33. Bartholomew GA. The water economy of seed-eating birds that survive without drinking. Proc Int Ornithol Congr. 1972;15:237–254.
34. Marder J, Ben-Asher J. Cutaneous water evaporation I. Its significance in heat-stressed birds. Comp Biochem Physiol A Comp Physiol. 1983;75(3):425–431.
35. Marder J, Gavrieli-Levin I. The heat-acclimated pigeon: an ideal physiological model for a desert bird. J Appl Physiol (1985). 1987;62(3):952–958.
36. Webster MD, Bernstein MH. Ventilated capsule measurements of cutaneous evaporation in mourning doves. The Condor. 1987;89(4):863‒868.
37. Wolf BO, Walsberg GE. Respiratory and Cutaneous Evaporative Water Loss at High Environmental Temperatures in a Small Bird. Journal of Experimental Biology.1996;199:451‒457.
38. Arieli Y, Peltonen L, Ophir E. Cooling by cutaneous water evaporation in the heat-acclimated rock pigeon (Columba livia). Comp Biochem Physiol A Mol Integr Physiol. 2002;131(3):497–504.
39. Ophir E, Arieli1 Y , Marder J, et al. Cutaneous blood flow in the pigeon Columba livia: it’s possible relevance to cutaneous water evaporation. J Exp Biol. 2002;205(Pt 17):2627–2636.
40. McKechnie AE, Wolf BO. Partitioning of evaporative water loss in white-winged doves: plasticity in response to short-term thermal acclimation. J Exp Biol. 2004;207(Pt 2):203‒210.
41. DeNardo DF, Zubal TE, Hoffman TCM. Cloacal evaporative cooling: a previously undescribed means of increasing evaporative water loss at higher temperatures in a desert ectotherm, the Gila monster Heloderma suspectum. J Exp Biol. 2004;207(Pt 6):945‒953.
42. Hoffman TC, Walsberg GE, DeNardo DF. Cloacal evaporation: an important and previously undescribed mechanism for avian thermoregulation. J Exp Biol. 2007;210(Pt 5):741‒749.
43. Even PC, Nadkarni NA. Indirect calorimetry in laboratory mice and rats: principles, practical considerations, interpretation and perspectives. Am J Physiol Regul Integr Comp Physiol. 2012;303(5):R459‒R476.
44. Hoffman TCM, Walsberg GE. Inhibiting ventilatory evaporation produces adaptive increase in cutaneous evaporation in mourning doves, Zenaida macroura. J Exp Biol. 1999;202(Pt 21):3021‒3028.
45. Marder J, Arieli Y, Ben-Asher J. Defense strategies against environmental heat stress in birds. Israel Journal of Zoology. 1989;36(2):61–75.
46. Webster MD, King JR. Temperature and humidity dynamics of cutaneous and respiratory evaporation in pigeons, Columba livia. J Comp Physiol. 1987;157(2):253‒260.
47. Withers PC, Williams JB. Metabolic and respiratory physiology of an arid-adapted Australian bird, the Spinifex pigeon. The Condor. 1990;92(4):961‒969.
48. Frappell P, Hinds DS, Boggs D. F Scaling of Respiratory Variables and the Breathing Pattern in Birds: An Allometric and Phylogenetic Approach. Physiol Biochem Zool. 2001;74(1):75–89.
49. Williams JB, Munoz-Garcia A, Ostrowski S, et al. A phylogenetic analysis of basal metabolism, total evaporative water loss, and life-history among foxes from desert and mesic regions. J Comp Physiol B. 2004;174(1):29–39.
50. Williams JB, Tieleman BI. Ecological and evolutionary physiology of desert birds: A Progress Report. Integ Comp Biol. 42(1):68–75.
51. Clark CJ, Dudley R. Flight costs of long, sexually selected tails in hummingbirds. Proc Biol Sci. 2009;276(1664):2109‒2115.
52. Clark CJ, Dudley R. Hovering and forward flight energetics in Anna's and Allen's Hummingbirds. Physiol Biochem Zool. 2010;83(4):654‒662.
53. Dargoltz VG. The caloric equivalent of body weight changes of homoiothermal animals: relationship between oxidized substances and heat loss through evaporation. Zh Obshch Biol.1973;34:887‒898.