Heterogeneity in genetic diversity and differentiation is a reflection of various past demographic events and evolutionary forces (Gene flow, divergence, Bottlenecks, mutations, selection etc.) that may have shaped the existing DNA polymorphisms in the genetic data. The gadwall (Anas strepera) is a waterfowl species that has a holoarctic distribution across North America (New World) and Eurasia (Old World), while the Asian Falcated duck (A. falcata) has a restricted distribution across Eastern Asia, where the two species share their breeding ranges. Previous studies revealed a strong structure between the Old World and New World gadwall populations and a high among locus heterogeneity in the genetic diversity. In this study, we assessed the rates of introgression between the falcated duck and gadwall populations under three coalescent models of introgression using a genomic transect of non–coding DNA. We sampled nineteen nuclear introns that mapped to nineteen different chromosomes and evaluated all three population isolation–with migration models of coalescent history between the gadwalls and falcated ducks. The results revealed introgression from falcated duck population into NW gadwall population, but not into OW gadwall population or from any gadwall population into Asian falcated duck population. The nucleotide diversity in the falcated duck varied over 100–fold among the nineteen loci, however the genetic differentiation varied more than 20 fold among the sequenced loci. Using this comprehensive dataset, we conclude that hybridization alone is insufficient to explain the observed among–locus heterogeneity in genetic diversity in the non–coding DNA of both waterfowl species suggesting a prominent role of selection.

Keywords: hybridization, gadwalls, introgression, genetic diversity, falcated ducks

Genetic diversity quantifies the neutral and non–neutral variation in a population that the interactions between the demographic and evolutionary forces (population size changes, subdivision, mutations, immigration and selection) generate. Empirical evidence suggests the diversity has a positive correlation to population size. Loss in diversity results in the bottlenecks and rare allele generation retains the diversity in population expansion. Mostly, diversity is small in the island population relative to the mainland population.¹ Similarly, loss in variation is evident in the endangered species. However, this positive correlation between diversity and population size is not justified at all the markers. In nuclear DNA, population size reflects a positive relationship with diversity, but the relationship is ambiguous at mtDNA implying deviations from neutral theory and the possible role of selective sweeps, recombination, mutation rate and linkage disequilibrium.¹⁻³

Levels of genetic diversity and differentiation can vary extensively across the genomes of a population or species.⁴⁻¹¹ Some level of heterogeneity is expected from the stochasticity of mutation, genetic drift, non–random mating and gene flow, under models of neutral population history.¹²⁻¹⁴ However, given increasing evidence of non–neutrality of loci across the genome, the contribution of selection to this heterogeneity cannot be ignored.^1,15,16 In the absence of gene flow, positive selection, for example, can cause selectively advantageous alleles arising via mutations to spread throughout a population, resulting in low genetic variation and low differentiation at loci under selection, and closely linked loci.¹⁷ Likewise, strong negative selection eliminates deleterious polymorphisms from linked sites within a genome in a population.¹⁸ Both types of selection can cause an excess of rare polymorphisms, which can mimic the signature of a population expansion.¹⁹ On the other hand, balancing selection maintains high levels of genetic diversity at some loci and prevents population divergence.^18,20 Balancing selection can result in a paucity of rare polymorphisms, mimicking a population bottleneck. Hence, disentangling the roles of various evolutionary forces to among–locus heterogeneity can be difficult as selection can mimic the effects of population history.

Although distinguishing between the genomic influence of population history and selection is difficult, both must be considered to understand the genomic effects of the other. Hybridization and introgression can modify the diversity and divergence at a locus by causing new alleles to enter a species gene pool.²¹⁻²⁴ However, variability in the interaction between gene flow and selection across the genome can drive heterogeneous patterns of divergence and diversity. Positive selection may favour introgression of alleles and allow for homogenization of genomes at some loci,^25,26 but divergent selection may prevent gene flow at loci that maintain species integrity causing an increase in genetic differentiation at those loci.²⁷⁻³¹ Likewise, a locus that has high gene flow under the influence of positive selection is likely to have low diversity (gene swamping) when the mutational force is not effective.³² Thus, genetic variation and divergence of various loci could be subject to variable selective pressures that filters introgression of alleles at some loci but not at others.^18,33−35 The objective of this study is to examine the role of demography and gene flow on genomic heterogeneity observed in gadwall populations.

Study taxa

The gadwall (Anas strepera) is a species of duck distributed across Eurasia (Old World, OW) and North America (New World, NW; Figure 1). The sequence data from twenty–two non–coding loci in the gadwall (Anas strepera) revealed large among–locus heterogeneity in genetic diversity that varied by two orders of magnitude.¹⁰ OW and NW populations are characterized by haplotype frequency differences in mitochondrial (mt) DNA and nuclear (nu) DNA that likely resulted from a founder effect (colonization of NW from OW) and restricted gene flow.^10,36 Intragenomically, the observed among–locus heterogeneity failed to fit this model of population history. However, neither selection nor interspecific hybridization could be rejected as plausible explanations.

The gadwall hybridizes with its closest extant relative, the falcated duck (Anas falcata), in the wild.³⁷ Unlike the gadwall, the falcated duck has a restricted distribution in eastern Asia, where its breeding range overlaps with the gadwall (Figure 1). Molecular data revealed introgression of falcated duck alleles into the gadwalls. Falcated duck shared one haplotype each at mtDNA and one of the two nuclear loci sequenced with sympatric OW gadwalls.³⁸ In addition, 5.5% of North American gadwalls had mtDNA that was more similar to falcated ducks than to other gadwalls, although there was no evidence of nuclear introgression.^38,39 Because this assessment of introgression was based only on the two nuclear loci with one marker linked to the Z–chromosome that may be less susceptible to introgression,^5,40 a multi–locus assessment is necessary to examine the extent of nuclear introgression to better examine its role in among–locus heterogeneity.

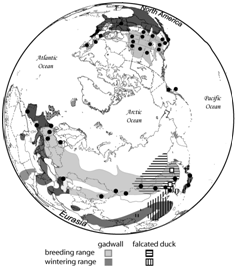
Figure 1 Geographic distribution of falcated ducks in eastern Asia and gadwalls across Europe, Asia, and North America. Black dots and open squares represent sampling locations of gadwalls and falcated ducks, respectively. Modified from Peters et al.,³⁰ and Sampling details are available in Peters et al.¹⁰

The main objectives of this study were:

1. To examine genetic diversity sampled from genomic transect in falcated ducks and compare it to the among–locus heterogeneity observed in gadwall;
2. To estimate rates of introgression between species in sympatry and allopatry; and
3. To examine the role of introgression in among–locus heterogeneity in genetic diversity and differentiation. This multi–locus comparison of polymorphic data between falcated ducks and the gadwall populations will facilitate disentangling the roles of introgression and selection in generating among–locus heterogeneity in these taxa.

We sequenced a genomic transect for 24 falcated ducks (Figure 1), which included nineteen non–coding regions of nuclear DNA that map to different chromosomes in the chicken (Gallus gallus) genome using previously published primers (60; Table 1). Homologous data for 25 NW and 25 OW gadwalls were obtained from Peters et al.¹⁰ Each locus was amplified using PCR and cleaned using AMPure XP beads following the Agencourt protocol (Beckman Coulter Co., Brea, CA).We sequenced PCR products using the BigDye v. 3.1 Terminator Cycle Sequencing Kit following manufacturer protocols (Applied Biosystems, Foster City, CA). Automated sequencing was performed on an ABI 3730 at the DNA Sequencing Facility on Science Hill, Yale University, CT. We edited the falcated duck sequences and aligned them with gadwall sequences using Sequencher 4.1 (Gene Codes, Ann Arbor, MI). We determined the gametic phases of sequences that were heterozygous at more than one nucleotide position using the software PHASE 2.1.^41,42 The data will be archived in GenBank and DRYAD (Accession number pending).

Genetic diversity and demography

We quantified genetic variation within the populations and differentiation among populations in terms of the nucleotide diversity (π, the average number of nucleotide differences per site between two randomly selected individuals from a population), pairwise $ФST$ (the proportion of genetic diversity attributable to differences among populations), and Tajima’s D (a measure of the relative frequency of rare polymorphisms to common polymorphisms) in Arlequin v3.11.⁴³ We used linear regression to compare π between falcated ducks and gadwalls. A paired t–test was used to compare $ФST$ between falcated ducks and gadwalls with $ФST$ between the two gadwall populations with locus being the paired variable. We constructed haplotype networks using the median–joining algorithm in NETWORK ver. 4.1.⁴⁴

To infer aspects of the population histories of falcated ducks and OW and NW gadwalls, we applied the MCMC Bayesian approach in a three–population isolation with migration model in the coalescent program IMa2.^41,42,45,46 Demographic history was estimated under three possible scenarios of migration: a full migration model with both ancestral and ongoing gene flow, a model of recent secondary contact that assumes no gene flow between ancestral populations, and a model of ancestral migration that assumes no ongoing migration. The estimated parameters included time since divergence (t₀ and t₁, the divergence times between OW and NW gadwalls and between falcated ducks and gadwalls, respectively, where t=Tµ; T is the time since divergence in years and µ is the geometric mean of mutation rates per locus among all loci), the effective population sizes of the ancestral populations (θ_A0 at t₀ and θ_A1 at t₁, where θ_A=4N_eAµ and N_eA is the ancestral effective population size), and the effective population size of each daughter population (θ_f, θ_ow, and θ_nw, for falcated ducks, OW gadwalls and NW gadwalls, respectively). The full migration model included eight migration parameters (M_ij): two parameters (bidirectional migration) between pair of populations and between the falcated duck and the ancestral gadwall population (where M_ij=m_i/µ and m_i is the rate at which alleles enter population j from population i forwards in time). The model of secondary contact only included migration between extant populations (six migration parameters), whereas the ancestral migration model only included migration between the two gadwall populations and between the falcated duck and the ancestral gadwall population (four parameters). We converted migration rates into the number of effective migrants per generation as θm_ij /2. Because IMa2 assumes no recombination within loci, We chose the block of nucleotides consistent with no recombination that contained the maximum number of variable sites for each locus in IMgc.⁴⁷ We iteratively adjusted the chromosomal weighting so that a maximum of 5% of chromosomal copies were removed from the analysis. IMgc was only used as a guide for truncating sequences, and we retained all sites that contained three or four nucleotides. Inheritance scalars were defined to respect different modes of inheritance (0.75 for CHD1Z & 1.0 for autosomal loci). An HKY model of molecular evolution was used for X loci, and an infinite sites model was used for the remaining loci. We ran IMa2 on the recombination–filtered, nineteen–locus data set for 2x107 steps following a burn–in of one million steps using thirty markov chains (one hot and 29 cold chains). We replicated the analysis three times with different random number seeds to check for convergence.

We also used the MCMC Bayesian method in the coalescent program LAMARC v2.1.6 (42) to jointly estimate recombination rates (r, where , $r=C/\mu$ C is the rate of recombination per inter−site link per generation, and $\mu$ is the mutation rate per site) for each locus in falcated duck. We jointly estimated $\Theta$ (where $\Theta$  = $4N_e\mu$ , and $N_e$ is the effective population size) and the exponential growth rate (g, where ${\Theta }_t={\Theta }_{o}ex{p}^{-gt}$ , and ${\Theta }_o$ is an index of the current $N_e$ and ${\Theta }_t$ is an index of $N_e$ at time t). We used the Felsenstei006E 84 model of substitution (ti:tv=2.5; the average ratio among loci) and ran the program for a burn−in of 2,000,000 generations, sampling every 1,000 generations for a total of 20,000 samples. To verify the consistency of the estimates, we replicated the run with a different random number seed.

Coalescent simulations

We simulated genetic diversity and differentiation in each population to assess the role of introgression in the among–locus heterogeneity in genetic diversity under the assumptions of neutrality. For these simulations, We followed the protocol described by Peters et al.,¹⁰ which incorporated the demographic parameters estimated from isolation–with–migration models, recombination rates from the LAMARC analyses, and evolutionary substitution rates estimated from a comparison of eight deeply divergent anseriform taxa (obtained from Peters et al.¹²). We simulated genetic diversity and differentiation under each of the three migration models: full migration, secondary contact, and ancestral migration. For each parameter, we randomly sampled 1000 values from their respective posterior distributions so that uncertainty in these values was incorporated in the simulations.

Simulations were conducted under an assumption of neutral population history in the program MS.⁴⁸ All parameters were scaled to θf, and the parameters for CHD1z were scaled by a factor of 0.75 to reflect the difference in effective population size resulting from linkage to the sex–chromosome Z. Polymorphism data were simulated 1,000 times for each locus (each replicate had a slightly different population history as described above) under each of the three models (19,000 simulations per model). From each simulated data set, We calculated π, ΦST, and Tajima’s D using the program MS output.¹⁰

Goodness–of–fit test

We performed a goodness–of–fit test to test to examine of the empirical data to the models of population history (7, 60). For the population level goodness–of–fit tests, we compared empirical values of mean π and ΦST and their associated coefficients of variation (CV) with the expected values for a 19–locus dataset obtained from the simulated data (1,000 values per model). We also compared locus–specific values of each parameter to determine whether any loci were consistent outliers from model expectations. We rejected the null hypothesis of no difference between expected and empirical values if the empirical values were outside the 95% CI of expected values.

Genetic variation and population structure

Sequence data from 19 non–coding loci revealed that heterogeneity in nucleotide diversity (π) for the falcated duck was similar to that observed in NW and OW gadwall populations (Table 2). Overall, π in falcated duck (mean π=0.0097, range =0.0002–0.0251) was similar to values observed in both OW (mean π=0.0091, range=0.0001–0.0231) and NW (mean π=0.0090, range=0.0001–0.0243) gadwalls. Indeed, nucleotide diversity among the 19 loci in falcated ducks was significantly correlated to that in OW gadwalls (R2=0.88, df=18, P=3 x10–9) and NW gadwalls (R2=0.80, df=18, P=2x10–7). Average Tajima’s D was negative for each of the three populations (DFD=–0.52+0.97 StDev; DOW=–0.44+0.79 StDev; DNW=–0.11+0.74 StDev) and was significantly negative for four loci in falcated ducks (CRYAB, FAST, LDHB GRIN1) and OW gadwalls (Sf3A2, ENO1, FAST, GRIN1) and for two loci in NW gadwalls (Sf3A2, GRIN1) (Table 2).

Population pairwise comparisons indicated that falcated duck is significantly differentiated from both gadwall populations (mean ΦST (OW–FD)=0.281, range=0.035–0.965; mean ΦST (NW–FD)=0.286, range=0.032–0.901; Table 2). Differentiation was significantly lower between OW and NW gadwalls (ΦST (OW–NW)=0.057, range=–0.014–0.184; t=1.73, df=18, P<0.005). The haplotype networks revealed that many polymorphisms were shared between falcated ducks and gadwalls at most of nuclear loci; only CRYAB, LDHB and CHD1Z were consistent with reciprocal monophyly between the species (Figure 1). On the other hand, NW and OW gadwalls shared alleles at all loci.

Demographic history, migration, and divergence

The three–population model with all migration parameters in IMa2 showed a finite posterior distribution for most of the demographic parameters (Figure 3), (Table S1). In this model, ${\theta }_{FD}$ was the largest among all θ parameters ( ${\theta }_f$ = 2.1, 95% HPD= 1.6–2.9). There was no overlap in the 95% HPD between ${\theta }_f$ and ${\theta }_{nw}$ , which had the smallest population size ( ${\theta }_{nw}$ = 0.61, 95% HPD=0.26–0.93). On the other hand, ${\theta }_{ow}$ was intermediate ( ${\theta }_{ow}$ =1.10, 95% HPD=0.63–2.06) with 95% HPDs that overlapped both θ_f and θ_nw. The ancestral population of gadwalls ( ${\theta }_{A0}$ ) was smaller than either NW or OW gadwall population (θ_A0=0.35, 95% HPD= 0.01–4.6)_, whereas the ancestral population of gadwall and falcated duck ( ${\theta }_{A1}$ = 0.66, 95% HPD= 0.14–1.40) was similar to that of NW gadwalls but smaller than OW gadwall and falcated duck. Thus, the model suggested population expansions for all three populations following divergence. Similar values of θ were obtained from both the secondary–contact and the ancestral migration models (Table 1) and (Figure 2). However, analyses of population size changes in falcated ducks obtained from LAMARC were consistent with a stable population size (g=–0.98, 95% CI=–8.8–37.2).

The estimates of time since divergence between the falcated duck and ancestral gadwall and the two gadwall populations peaked at different points in the full model (Figure 2), (Table S1). The model supported a deep divergence between the gadwall and falcated duck ( $t1$ =0.42, 95% HPD=0.25–1.6), but only a slightly more recent divergence between OW and NW gadwall ( $t0$ =0.35, 95% HPD=0.03–0.55). However, the posterior distribution of divergence time between OW and NW gadwalls was bimodal with a minor peak that was substantially more recent. In the secondary–contact model, $t1$ was similar to the full model, but t0 showed a broad posterior distribution that encompassed both peaks from the full model (Figure 2b), (Table 1). In the ancestral migration model, t1 was similar to the previous two models, whereas t0 was more recent and consistent with the minor peak in the full model ( $t0$ = 0.06, HPD 95%=0.02–0.11). Unlike the previous models, there was no overlap in the two divergence time estimates (Figure 2), (Table 1), and t0 was similar to the estimate obtained from the two–population model examined in Peters et al.¹⁰

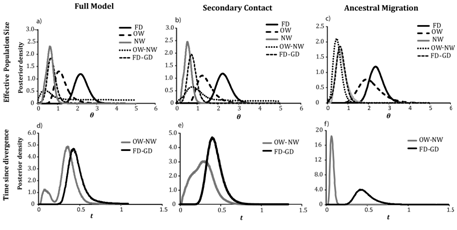
Figure 2 Posterior distributions of demographic parameters estimated in IMa2 (scaled to the neutral mutation rate) estimated under three migration models: full migration (a,d), secondary contact (b,e), and ancestral migration (c,f,); a,b,c) effective population sizes of the falcated duck, OW gadwall, NW gadwall and ancestral populations; def) Time since divergence between the falcated duck and gadwall and between OW and NW gadwalls.

In the full migration model, the rates of introgression from OW and NW gadwall into the falcated duck (forward in time) peaked at the lowest value of <0.001 (95% HPD=0–0.44 and 0–0.345, respectively; Table 1, Figure 3). Thus, the model was consistent with little to no introgression from gadwalls into falcated ducks. Similarly, the introgression rate from falcated ducks into OW gadwalls peaked near zero (MFD→OW <0.001, 95% HPD=0–0.411). However, gene flow from falcated ducks into NW gadwalls was low, but non–zero (2NmFD→NW=0.26 migrants per generation, 95% HPD=0.02–0.50). Likewise, the estimates of gene flow between the ancestral populations in the full model suggested asymmetrical gene flow with higher migration rates from the falcated duck into the ancestral gadwall population, although confidence intervals were large and we could not reject the possibility of no gene flow (2NmFD→A0=0.56 migrants per generation, 95% HPD=0–78.2; 2NmA0→FD=0.051 migrants per generation, 95% HPD=0–54.0). The model also supported asymmetrical gene flow between the two gadwall populations with higher gene flow into the OW population (2NmNW→OW=2.2 migrants per generation, 95% HPD=0–20.2; 2NmOW→NW=1.04, 95% HPD=0–7.07); however the posterior distribution of 2NmNW→OW was bimodal and the minor peak was consistent with no gene flow. These estimates of migration rates were similar in the model of recent secondary contact (no ancestral gene flow), suggesting gene flow into NW gadwalls from falcated ducks and little to no gene flow between the remaining interspecific pairs (Figures 3d–3f), (Table 1). Moreover, the posterior distribution of 2NmNW→OW was bimodal, but the minor peak was much smaller than in the full model. In contrast, all the estimates of migration rates had unimodal distributions in the ancestral migration model (Figure 3g), (Table 1). There was clear evidence of gene flow from the falcated duck into the ancestral gadwall population (2NmFD→A1=0.78, HPD 95%=0.41–1.36), but the posterior distribution was most consistent with zero gene flow in the opposite direction (2NmA1→FD= 0.027, HPD 95%=0–0.96). Similarly, the model estimated asymmetrical gene flow between the gadwall populations with greater introgression from the OW into the NW gadwall population (2NmOW→NW=4.53, 95% HPD=0.96–7.81; 2NmNW→OW=1.92, 95% HPD 95%=0–10.3), which was the reverse direction compared to the full migration model and the secondary–contact model, but consistent with the 2–population model examined in Peters et al.¹⁰

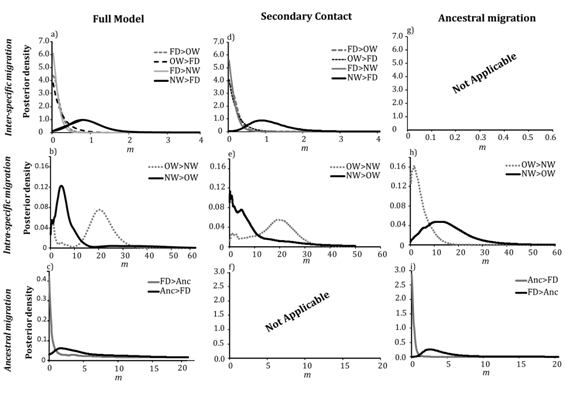
Figure 3 Posterior distributions of migration rates estimated in IMa2 in three migration models: full migration, secondary contact, and ancestral migration; a,d,g) interspecific migration rates between falcated duck and gadwall populations; b,e,h) migration estimates between the OW and NW gadwall populations; c,f,i) migration estimates between the falcated duck and ancestral population.

Simulated models of population history

To test the role of introgression in among–locus heterogeneity, we simulated DNA sequences using the parameters estimated from the three models of demographic history and selective neutrality. Simulations under all the three models under–predicted mean π within each population (Figure 4a) and mean $ФST$ between the falcated duck and each gadwall population (Figure 4b). Furthermore, empirical values of π and $ФST$ were within the 95% confidence intervals of the simulated values under the full migration model only. Mean π was significantly higher than expected for all three populations under the secondary–contact and ancestral–migration models, and ΦST between gadwalls and falcated duck was significantly greater than expected under secondary contact. The observed among–locus heterogeneity (coefficients of variation) in the data was significantly higher than the values simulated under all three migration models for all parameters, except $ФST$ between OW and NW gadwalls (Figure 4).

Locus–specific goodness–of–fit tests revealed that 13 of the 19 loci had significantly greater (GHRL, MSTN, LCAT, ODC1 NCL, SAA and CPD) or lower diversity (CRYAB, Sf3A2, FGB, LDH1, GRIN, CHD1z) than expected for at least one population (Figure 5). Nucleotide diversity for four loci (GHRL, LCAT, LDHB and MSTN) consistently differed from expectations in both taxa and under all three migration models (Fig. 5). Similarly, locus–specific tests for $ФST$ between falcated duck and gadwall revealed four loci (CRYAB, CHD1Z, GH1 and LDHB) in which the empirical levels of differentiation deviated significantly from the simulated values (Figure 6). At all four loci, the empirical values of $ФST$ were greater than expected for both population pairs. However, empirical values of $ФST$ between the two gadwall populations were consistently within the simulated values for all 19 loci.

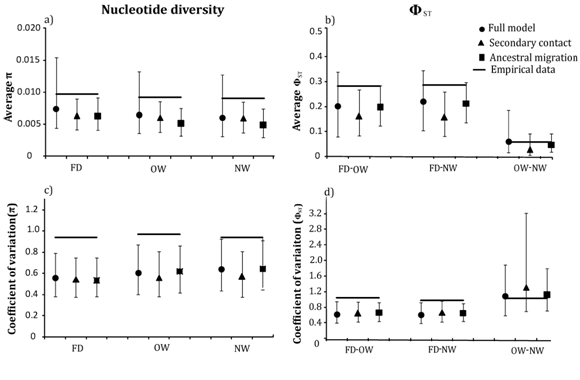
Figure 4 Empirical and simulated values of a) mean nucleotide diversity for the nineteen locus data for each population b) mean ΦST between each population pair c) coefficients of variation for nucleotide diversity in falcated ducks, OW gadwall, and NW gadwall, and d) ΦST between each population pair under three migration models. Black circles, triangles and squares represent the simulated values for the full migration model, secondary contact, and ancestral migration model, respectively; the horizontal bars show the empirical values.

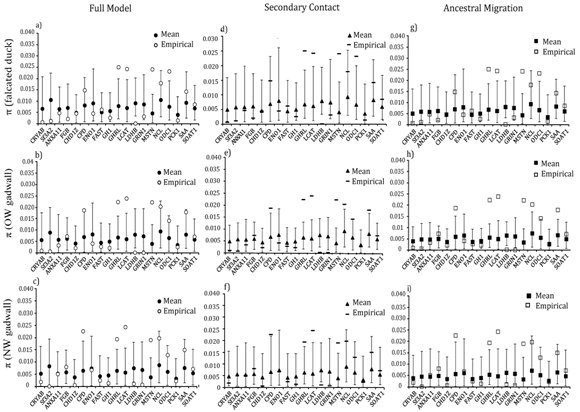
Figure 5 Locus-specific goodness of fit tests for nucleotide diversity in the falcated duck, OW gadwall, and NW gadwall under three migration models: full migration (a,b,c), secondary contact (d,e,f), and ancestral migration (g,h,i). Open symbols mark the empirical data; filled symbols mark the expected values (and the 95% confidence interval) under each model.

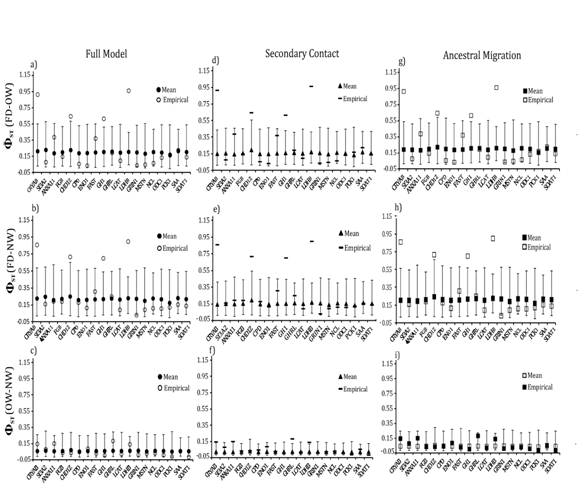
Figure 6 LLocus-specific goodness-of-fit tests for mean ΦST between each population pair under the full migration model (a,b,c), secondary contact (d,e,f), and ancestral migration (g,h,i). Open symbols mark the empirical data; filled symbols mark the expected values (and the 95% confidence interval) under each model.

Among–locus heterogeneity in genetic diversity is generated in interplay among various genomic and demographic forces that randomly add and remove variation in the genome. Peters et al.,¹⁰ proposed introgression or selection as likely hypotheses that can explain the observed heterogeneity in the gadwall populations in the North America and Eurasia. In this study, we evaluated three three–population isolation–with–migration models of coalescent history between the gadwalls and falcated duck (ancestral migration, secondary contact and full migration) with nineteen nuclear introns that mapped to nineteen different chromosomes. In all three demographic scenarios of introgression between the falcated duck and two gadwall populations, there was an evidence of gene flow in allopatry from falcated duck into north American gadwalls but not in sympatry into the Eurasian gadwalls. There was no evidence of any gene flow from any of the gadwall population into the falcated duck population. Simulating diversity under neutral demographic history of gene flow, four loci consistently deviated from the neutral expectations in both gadwall populations and falcated duck in all three isolation–migration models. Furthermore, these results revealed lower–than–expected nucleotide diversity for LDHB and higher–than–expected differentiation at both LDHB and CHD1Z, which combined with regular selective sweeps in mtDNA.⁴⁹⁻⁵² likely mislead the results in Peters et al.¹⁰ As observed in the gadwall, nucleotide diversity in the falcated duck varied over 100–fold among the 19 loci, yet we found no evidence of DNA introgression from gadwall into falcated duck. Furthermore, differentiation between the falcated duck and the gadwall varied more than 20–fold among the sequenced loci, which was greater than expected under the inferred neutral models. Therefore, we reject introgression alone as the cause of observed among–locus heterogeneity in both gadwall populations and the falcated duck and propose influence of selection, rather than hybridization, as a better explanation for the among–locus heterogeneity observed in both taxa.

Deviations from the models

Coalescent analyses of nuDNA supported introgression either from falcated ducks into allopatric NW gadwalls or from falcated ducks into the ancestral gadwall population but not into sympatric OW gadwalls. Previous mtDNA analysis also revealed this direction of gene flow and evidence for ancient introgression into NW gadwalls, although ongoing gene flow could not be rejected in sympatry.³⁸ In this sense, analyses of mtDNA and nuDNA provide concordant results suggesting that NW gadwalls harbor a significant proportion of falcated duck DNA within their gene pool. Whatever the true scenario might be (ancient or ongoing gene flow), introgression fails to account for the among–locus heterogeneity in genetic diversity in these taxa.

First, the goodness–of–fit tests revealed a poor fit between empirical data and the neutral models of demographic history under all three migration scenarios. Specifically, the empirical coefficients of variation for diversity and interspecific differentiation failed to fit within the expected simulated values under all three models (Figure 4). Similarly, several loci had values of genetic diversity and differentiation that deviated significantly from the expected values under all three neutral models (Figures 5), (Figure 6). The stochasticity of mutation and drift is unlikely to explain this high heterogeneity as the tested models incorporated the variance in these evolutionary forces. Locus–specific mutation rates estimated from independent data and uncertainty in coalescent estimates of population–level parameters were also incorporated. Given the amount of noise included in the simulated models, the deviations from the expected patterns are particularly striking.

Secondly, genetic variation in nuDNA is expected to reflect the species abundance and distributions,^2,3,53 and therefore, we expected the smaller population of falcated duck (estimated census size of 90,000 individuals⁵⁴ to have lower diversity than the more abundant Holarctic gadwall (>3,000,000 individuals; 17). However, despite the thirty–times smaller population size of falcated duck relative to gadwall, the two species had similar genetic diversity, and the falcated duck had the largest effective population size in all three coalescent models that we examined. A large historical population size in the falcated duck followed by a recent population decline could be one possible explanation for the observed deviation. However, analyses of population size changes were consistent with falcated ducks having had a stable population size, and there was no evidence of a major population decline. Alternatively, a much smaller ancestral population size for gadwalls followed by a population expansion could explain this deviation, which is supported by coalescent analyses.^10,36 Regardless, this deviation from expectations questions the relative roles of genetic drift, introgression, and selection. The large effective population size in falcated duck relative to gadwall, the lack of evidence of gene flow into falcated duck from any of the gadwall populations, and a lack of evidence suggesting a major population decline in falcated duck, suggest that selection might be playing an important role.

Locus–specific deviations

The available evidence suggests that selection is a strong candidate for the cause of at least some of the among–locus heterogeneity in these taxa. We propose two markers (CRYAB and LDHB) as candidate loci under strong positive selection for their exceptional patterns. Both loci have lower genetic diversity than predicted for both gadwall populations and for falcated ducks. CRYAB and LDHB are also more strongly differentiated between falcated ducks and gadwalls than predicted and among the most differentiated loci between the two gadwall populations. These loci were also more differentiated, relative to other loci, between populations of other species of ducks (CRYAB and LDHB in green–wing teal Anas crecca and CRYAB in common merganser Mergus merganser^55,56).

LDHB, the locus with the lowest diversity and the highest divergence, appeared consistently as an outlier in sixteen of eighteen sets of simulated data under all three models of population history. All three models over–predicted the diversity for this locus in all three populations and under–predicted the divergence between falcated ducks and gadwalls. LDHB was the only locus among the nineteen loci that never conformed to neutral expectations. Also, the near star–like pattern of the network topology and a significantly negative Tajima’s D are consistent with positive selection that may have increased the levels of genetic differentiation among populations.^51,58 Functionally, the gene is expressed both in the heart of ducks and in the eyes as lens structural proteins (ε–crystalline; 28), and there is evidence of adaptive evolutionary changes occurring in the sequence of LDHB.^58,59 For example, the presence or absence of repressor elements in the regulatory sequence of LDHB is responsible for the adaptive difference in LDHB transcription between northern and southern populations of Fundulus heteroclitu.⁶⁰ The high divergence of the locus and its association with adaptive evolution in other species supports the proposed hypothesis of non–neutrality at this locus.

CRYAB, also a low diversity locus with high differentiation, also failed to fit with the expected values under neutrality in several tests. A significant excess of rare polymorphisms and a star like pattern in the haplotype network topology support the possibility of positive selection/selective sweep at this locus. The evolutionary trajectory of this gene, which codes for eye–lens crystallins, varied slightly between mammalian and avian taxa. In contrast to the high conservation of the gene among mammals, only a few blocks of the gene are conserved in birds. For example, the duck CRYAB homologues have lost the heat shock response seen in mammalian homologues.⁶¹ This partial conservation of gene elements in ducks and the variability in heat–shock response suggest taxon–specific patterns of expression and perhaps divergent selection. It is intriguing that both CRYAB and LDHB are expressed in eye–lens crystallins and both deviate from neutral expectations.

Genetic hitchhiking can influence nucleotide diversity of non–coding loci and potentially maintain the high diversity of non–coding regions (several times that of neutral loci), when these regions are in linkage disequilibrium with a coding region under balancing selection.^45,62,63 Alternatively, hitchhiking can cause reduced variation in non–coding DNA linked to loci subjected to selective sweeps.^62,64 Thus, elevated or reduced diversity in non–coding regions might not necessarily be due to selection acting directly on components of the introns, but rather a result of strong linkage to coding regions that are the targets of selection. Hitchhiking depends upon the recombination rate and the distance from the target of selection.¹⁷ However, hitchhiking could be prominent in the non–coding loci with lower recombination rates. The major outlier loci, CRYAB and LDHB, in falcated ducks and gadwalls were both consistent with no intra–locus recombination.¹⁰ Therefore, selection on the coding regions of these loci coupled with hitchhiking could explain the inferred non–neutrality that was detected.

Kraus et al.,⁶⁵ suggested that hybridization among more divergent species of Anas ducks likely explained the high number of polymorphisms shared among species. Our models do not account for the possibility of gene flow with these additional species, and it is possible that this confounding variable could explain some of the heterogeneity that we observed. In particular, the high diversity loci might reflect broad introgression. However, broad–scale hybridization cannot fully account for the low diversity found at some loci (e.g. LDHB and CRYAB) without the combined effects of selection preventing the introgression of alleles at those loci. Thus, complete neutrality is unlikely even under this more complex population history.

Differential introgression, divergent selection, and demography

Heterogeneity in genetic divergence across the genome of divergent taxa is expected given a role of divergent selection. The counteraction between introgression and divergent selection prevents complete homogenization of genomes when divergent selection restricts gene flow at some loci. Therefore, these loci can have higher genetic differentiation than neutral loci.^{29,33,66−69} In accordance with the predictions of differential introgression caused by divergent selection, this study detected several outlier loci that exhibited higher genetic differentiation than expected under neutrality (Figure 6). The same outlier loci were observed under all three models of introgression. Despite evidence of introgression from falcated duck into the NW gadwall and limited gene flow between falcated duck and OW gadwall, the same four loci were detected as outliers in both comparisons. On the other hand, ΦST values for these loci were consistent with expectations under neutrality between OW and NW gadwalls, suggesting inter–specific selective pressures. In particular, the sex–linked locus CHD1Z was consistently an outlier and empirical data from numerous taxa suggest that the Z–chromosome is often less likely to introgress than autosomal chromosomes.^40,70,71 We found evidence of higher nuDNA introgression in allopatry, which was consistent with patterns observed in mtDNA.^36,38

Infrequent sightings of male falcated ducks in North America,

(http://www.fws.gov/sacramentovalleyrefuges/wo_sightings.html) raises the speculation of ongoing gene flow with NW gadwalls in accordance with Hubb’s Principle or Desperation hypothesis, which predicts hybridization when one species is rare in sympatry.⁷² Absence of conspecifics and restricted mate choice in North America could cause these rare Asian visitors to hybridize with the more abundant gadwalls, as has been demonstrated in other species of ducks.⁶⁸ Alternatively, the introgression of falcated duck genes into NW gadwalls could be explained by ancient introgression.³⁸ Genetic evidence suggests that the gadwall colonized North America from Eurasia during the late Pleistocene.³⁶ If a falcated duck or a hybrid was among the original founders, then it could have had a large genetic contribution to the extant gene pool. The observation that some mtDNA haplotype in NW gadwall were similar to, but not shared with, falcated duck haplotype is consistent with this scenario.³⁸ Furthermore, our model that allowed only ancient introgression converged better than the other migration models, suggesting that it might be a more appropriate model. Unfortunately, distinguishing between ancient gene flow and secondary contact can be difficult with genetic data^46,58 preventing conclusive tests of these hypotheses.

We conclude that gene flow between falcated ducks and gadwalls fails to explain the among–locus heterogeneity in genetic diversity and differentiation observed in these taxa. Simulating models of introgression under neutrality failed to explain the high empirical diversity for some loci (GHRL, LCAT and MSTN) and lower empirical diversity observed for other loci (LDHB and GRIN1). Inter–specifically, CRYAB and LDHB were strong outliers with exceptionally high values of ΦST, and these two loci were also among the most structured between OW and NW gadwall. We suggest CRYAB and LDHB as strong candidate loci under positive selection, perhaps resulting from low recombination and high linkage disequilibrium with polymorphisms in coding regions. Selection might also have had a major effect on other loci, such as CHD1Z, thereby contributing to the strong among–locus heterogeneity in genetic diversity and differentiation. Although it is impossible to reject all possible neutral scenarios that might have contributed to the observed heterogeneity, selection has likely had an important contribution.⁷³⁻⁷⁷

This study was funded by a grant from the National Science Foundation (DEB–0926162) and the College of Science and Mathematics at Wright State University. We thank Kim Bolender and Kendra Millam for their assistance with laboratory work, and John O. Stireman, Michael Raymer, Volker Bahn and Kevin Omland for providing insightful comments and suggestions on earlier drafts of this manuscript. We also thank the Michael Raymer lab and Life Science Informatics at the University of Alaska, Fairbanks for providing computer resources.

Authors declare that their in no conflict of interest.

1. Frankham R. How closely does genetic diversity in finite populations conform to predictions of neutral theory? Large deficits in regions of low recombination. Heredity. 2012;108(3):167‒178.
2. Bazin E, Glémin S, Galtier N. Population size does not influence mitochondrial genetic diversity in animals. Science. 2006;312(5773):570‒572.
3. Frankham R. Relationship of genetic variation to population size in wildlife. Conservation Biology. 1996;10.1500‒1508.
4. Avise JC. Phylogeography‒The history and formation of species. Cambridge: Harvard Univ Press; 2000.
5. Borge T, Webster MT, Andersson G, et al. Contrasting patterns of polymorphism and divergence on the Z chromosome and autosomes in two Ficedula flycatcher species. Genetics. 2005;171(4):1861‒1873.
6. Carneiro M, Blanco‒Aguiar JA, Villafuerte R, et al. Speciation in the European rabbit (Oryctolagus cuniculus): islands of differentiation on the X chromosome and autosomes. Evolution. 2010;64(12):3443‒3460.
7. Haddrill PR, Thornton KR, Charlesworth B, et al. Multilocus patterns of nucleotide variability and the demographic and selection history of Drosophila melanogaster populations. Genome Res. 2005;15(6):790‒799.
8. Hammer MF, Garrigan D, Wood E, et al. Heterogeneous patterns of variation among multiple human x‒linked loci: The possible role of diversity‒reducing selection in non‒Africans. Genetics. 2004;167(4):1841‒1853.
9. Nosil P, Feder JL. Widespread yet heterogeneous genomic divergence. Mol Ecol. 2012;21(12):2829‒2832.
10. Peters JL, Roberts TE, Winker K, et al. Heterogeneity in genetic diversity among non‒coding loci fails to fit neutral coalescent models of population history. Plos One. 2012c;7(2):e31972.
11. Strasburg JL, Sherman NA, Wright KM, et al. What can patterns of differentiation across plant genomes tell us about adaptation and speciation? Philos Trans R Soc Lond B Biol Sci. 2012;367(1857):364‒373.
12. Hudson RR, Turelli M. Stochasticity overrules the three‒times rule: Genetic drift, genetic draft, and coalescence times for nuclear loci versus mitochondrial DNA. Evolution. 2003;57(1):183‒190.
13. Knowles L, Richards CL. Importance of genetic drift during Pleistocene divergence as revealed by analyses of genomic variation. Mol Ecol. 2005;14(12):4023‒4032.
14. Rosenberg NA, Nordborg M. Genealogical trees, coalescent theory and the analysis of genetic polymorphisms. Nat Rev Genet. 2002;3(5):380‒390.
15. Ellegren H, Smeds L, Burri R, et al. The genomic landscape of species divergence in Ficedula flycatchers. Nature. 2012;491(7426):756‒760.
16. Hahn MW. Toward a selection theory of molecular evolution. Evolution. 2008;62(2):255‒265.
17. Smith JM, Haigh J. The hitch‒hiking effect of a favourable gene. Genet Res. 1974;23(1):23–35.
18. Charlesworth B, Nordborg M, Charlesworth D. The effects of local selection, balanced polymorphism and background selection on equilibrium patterns of genetic diversity in subdivided populations. Genet Res.1997;70(2):155–174.
19. Hughes AL. Near‒neutrality: the leading edge of the neutral theory of molecular evolution. Ann N Y Acad Sci. 2008;1133:162–179.
20. Charlesworth B, Morgan MT, Charlesworth D. The effect of deleterious mutations on neutral molecular variation. Genetics. 1993;134(4):1289–1303.
21. Johannesen J, Johannesen B, Griebeler EM, et al. Distortion of symmetrical introgression in a hybrid zone: evidence for locus‒specific selection and uni‒directional range expansion. J Evol Biol. 2006;19(3):705‒716.
22. Kaiser VB, Bergero R, Charlesworth D. A new plant sex‒linked gene with high sequence diversity and possible introgression of the X copy. Heredity. 2011;106(2):339‒347.
23. Minder AM, Widmer A. A population genomic analysis of species boundaries: neutral processes, adaptive divergence and introgression between two hybridizing plant species. Mol Ecol. 2008;17(6):1552‒1563.
24. Sweigart AL, Willis JH. Patterns of nucleotide diversity in two species of Mimulus are affected by mating system and asymmetric introgression. Evolution. 2003;57(11):2490‒2506.
25. Bachtrog D, Thornton K, Clark A, et al. Extensive introgression of mitochondrial DNA relative to nuclear genes in the Drosophila yakuba species group. Evolution. 2006;60(2):292‒302.
26. Currat M, Ruedi M, Petit RJ, et al. The hidden side of invasions: massive introgression by local genes. Evolution 2008;62(8):1908‒1920.
27. Kulathinal RJ, Stevison LS, Noor MA. The genomics of speciation in Drosophila: diversity, divergence, and introgression estimated using low‒coverage genome sequencing. PLoS Genet. 2009;5(7):e1000550.
28. Morjan CL, Rieseberg LH. How species evolve collectively: implications of gene flow and selection for the spread of advantageous alleles. Mol Ecol. 2004;13(6):1341‒1356.
29. Nosil P, Funk DJ, Ortiz‒Barrientos D. Divergent selection and heterogeneous genomic divergence. Mol Ecol. 2009;18(3):375‒402.
30. Noor MA, Grams KL, Bertucci LA, et al. Chromosomal inversions and the reproductive isolation of species. Proc Natl Acad Sci U S A. 2001;98(21):12084‒12088.
31. Schluter D. Ecology and the origin of species. Trends in Ecology Evolution. 2001;16(7):372‒380.
32. Lenormand T. Gene flow and the limits to natural selection. Trends in Ecology & Evolution. 2002;17(4):183‒189.
33. McCracken KG, Bulgarella M, Johnson KP, et al. Gene flow in the face of countervailing selection: adaptation to high‒altitude hypoxia in the betaA hemoglobin subunit of yellow‒billed pintails in the Andes. Mol Biol Evol. 2009;26(4):815‒827.
34. Postma E, van Noordwijk AJ. Gene flow maintains a large genetic difference in clutch size at a small spatial scale. Nature. 2005;433(7021):65‒68.
35. Storz JF, Kelly JK. Effects of spatially varying selection on nucleotide diversity and linkage disequilibrium: Insights from deer mouse globin genes. Genetics. 2008;180(1):367‒379.
36. Peters JL1, Zhuravlev YN, Fefelov I, et al. Multilocus phylogeography of a holarctic duck: colonization of North America from Eurasia by gadwall (Anas strepera). Evolution. 2008;62(6):1469‒1483.
37. Johnsgard PA. Hybridization in the Anatidae and its taxonomic implications. Condor. 1960;62(1):25–33.
38. Peters JL, Omland KE. Population structure and mitochondrial polyphyly in North American gadwalls (Anas strepera). Auk. 2007;124(2):444‒462.
39. Peters JL, Zhuravlev Y, Fefelov I, et al. Nuclear loci and coalescent methods support ancient hybridization as cause of mitochondrial paraphyly between gadwall and falcated duck (Anas spp.). Evolution. 2007;61(8):1992‒2006.
40. Storchová R, Reif J, Nachman MW. Female heterogamety and speciation: reduced introgression of the Z chromosome between two species of Nightingales. Evolution. 2010;64(2):456‒471.
41. Stephens M, Donnelly P. A comparison of Bayesian methods for haplotype reconstruction from population genotype data. Am J Hum Genet. 2003;73(5):1162‒1169.
42. Stephens M, Smith NJ, Donnelly P. A new statistical method for haplotype reconstruction from population data. Am J Hum Genet. 2001;68(4):978‒989.
43. Excoffier L, Lischer HE. Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under linux and windows. Mol Ecol Resour. 2010;10(3):564‒567.
44. Bandelt HJ, Forster P, Röhl A. Median‒joining networks for inferring intraspecific phylogenies. Mol Biol Evolution. 1999;16(1):37‒48.
45. Hey J. Isolation with migration models for more than two populations. Mol Biol Evol. 2010;27(4):905‒920.
46. Strasburg JL, Rieseberg LH. How robust are "Isolation with Migration" analyses to violations of the IM Model? A simulation study. Mol Biol Evol. 2010;27(2):297‒310.
47. Woerner AE, Cox MP, Hammer MF. Recombination‒filtered genomic datasets by information maximization. Bioinformatics. 2007;23(14):1851‒1853.
48. Hudson RR. Generating samples under a Wright‒Fisher neutral model of genetic variation. Bioinformatics. 2002;18(2):337‒338.
49. Ballard JW, Whitlock MC. The incomplete natural history of mitochondria. Mol Ecol. 2004;13(4):729‒744.
50. Hurst GD, Jiggins FM. Problems with mitochondrial DNA as a marker in population, phylogeographic and phylogenetic studies: the effects of inherited symbionts. Proc Biol Sci. 2005;272(1572):1525‒1534.
51. Galtier N, Depaulis F, Barton NH. Detecting bottlenecks and selective sweeps from DNA sequence polymorphism. Genetics. 2000;155(2):981‒987.
52. Galtier N, Nabholz B, Glémin S, et al. Mitochondrial DNA as a marker of molecular diversity: a reappraisal. Mol Ecol. 2009;18(22):4541‒4550.
53. McCusker MR1, Bentzen P. Positive relationships between genetic diversity and abundance in fishes. Mol Ecol. 2010;19(22):4852‒62.
54. Cao L, Barter M, Lei G. New Anatidae population estimates for eastern China: Implications for current flyway estimates. Biology Conservation. 2008;141(9):2301‒2309.
55. Peters JL, Bolender KA, Pearce JM. Behavioural vs. molecular sources of conflict between nuclear and mitochondrial DNA: the role of male‒biased dispersal in a Holarctic sea duck. Mol Ecol. 2012a;21(14):3562‒3575.
56. Peters JL, McCracken KG, Pruett CL, et al. A parapatric propensity for breeding precludes the completion of speciation in common teal (Anas crecca, sensu lato). Mol Ecol. 2012b;21(18):4563‒4577.
57. Becquet C, Przeworski M. Learning about modes of speciation by computational approaches. Evolution. 2009;63(10):2547‒2562.
58. Crawford DL, Powers DA. Molecular‒basis of evolutionary adaptation at the lactate dehydrogenase‒B locus in the fish Fundulus Heteroclitus. Proc Natl Acad Sci USA. 1989;86(23): 9365‒9369.
59. Kraft HJ, Voorter CE, Wintjes L, et al. The Developmental Expression of Taxon‒Specific Crystallins in the Duck Lens. Exp Eye Res. 1994;58(4):389‒395.
60. Schulte PM, Glemet HC, Fiebig AA, et al. Adaptive variation in lactate dehydrogenase‒B gene expression: Role of a stress‒responsive regulatory element. Proc Natl Acad Sci USA. 2000;97(12):6597‒6602.
61. Wistow G, Graham C. The duck gene for alpha‒B‒crystallin shows evolutionary conservation of discrete promoter elements but lacks heat and osmotic shock response. Biochim Biophys Acta. 1995;1263(2):105‒113.
62. Smith JM, Haigh J. Hitch‒Hiking Effect of a Favorable Gene. Genet Res. 1974;23(1):23‒35.
63. Orengo DJ, Aguade M. Detecting the footprint of positive selection in a European population of Drosophila melanogaster: multilocus pattem of variation and distance to coding regions. Genetics. 2004; 167(4):1759‒1766.
64. Kaplan NL, Hudson RR, Langley CH. The Hitchhiking Effect Revisited. Genetics. 1989;123(4):887‒899.
65. Kraus RH, Zeddeman A, van Hooft P, et al. Evolution and connectivity in the world‒wide migration system of the mallard: Inferences from mitochondrial DNA. BMC Genet. 2011;12:99.
66. Saint‒Laurent R, Legault M, Bernatchez L. Divergent selection maintains adaptive differentiation despite high gene flow between sympatric rainbow smelt ecotypes (Osmerus mordax Mitchill). Mol Ecol. 2003;12(2):315‒330.
67. Emelianov I, Marec F, Mallet J. Genomic evidence for divergence with gene flow in host races of the larch budmoth. Proc Biol Sci. 2004;271(1534):97‒105.
68. McCracken KG, Wilson RE. Gene low and hybridization between numerically imbalanced populations of two duck species in the Falkland Islands. Plos One. 2011;6(8):e23173.
69. Bamshad M, Wooding SP. Signatures of natural selection in the human genome. Nat Rev Genet. 2003;4(2):99‒111A.
70. Carling MD, Brumfield RT. Speciation in Passerina buntings: introgression patterns of sex‒linked loci identify a candidate gene region for reproductive isolation. Molr Ecol. 2009;18(5):834‒847.
71. Carling MD, Brumfield RT. Haldane's Rule in an avian system: using cline theory and divergence population genetics to test for differential introgression of mitochondrial, autosomal, and sex‒linked loci across the Passerina bunting hybrid zone. Evolution. 2008;62(10):2600‒2615.
72. Hubbs CL. Hybridization between fishes in nature. Systematic Zoology. 1955;4(1):1–20.
73. Delany S. Scott D. Waterbird Population Estimates. 4th ed. Wageningen: Wetlands International; 2006.
74. Hendriks W, Mulders JW, Bibby MA, et al. Duck lens epsilon‒crystallin and lactate dehydrogenase‒B4 are identical‒a single‒copy gene product with two distinct functions. Proc Natl Acad Sci U S A. 1988;85(19):7114‒7118.
75. Kuhner MK. LAMARC 2.0: maximum likelihood and Bayesian estimation of population parameters. Bioinformatics. 2006;22(6):768‒770.
76. Tajima F. Statistical methods for testing the neutral mutation hypothesis by DNA polymorphism. Genetics. 1989a;123(3):585–596.
77. Tajima F. The effect of change in population‒size on DNA polymorphism. Genetics. 1989b;123(3):597‒601.