The dynamics of the processes of cell maturation and regeneration is a branch currently in development for medicine, so taking advantage of the facilities of mathematics to model and solve environmental problems, different models of differential equations have been developed to describe these processes. From the existing deterministic models, the particular case of the hematopoietic cell is chosen, for of a comparative study on the influence of the medium on the process of cell maturation. For this, a probabilistic model of differential equations with six compartments is used. The stochastic term or environmental noise in this particular case modeled by a Weiner process. The inclusion of this term makes it possible to perform an analysis conditioned on the influence of the medium of the different processes of cellular maturation, in this case, of the hematopoietic cell. It is established that the stochastic model reflects a more precise approach to the clinical data used.

Keywords: deterministic models, hematopoietic cell, cell maturation, stochastic model

Stem cells are cells that have the ability to continually renew themselves by successive divisions and to specialize (differentiate) and become many types of body cells and, therefore, produce cells from one or several perfectly functional tissues. Stem cells can be divided without losing their properties, so that in most of the tissues of an adult there are populations of stem cells that, when divided, renew dead cells and regenerate damaged tissues. When a stem cell divides, each new cell can remain a stem cell or become another type of cell with a more specialized function, such as a muscle cell, a red blood cell or a heart cell.

The possibility to maintain in a culture stem cells for long periods of time (especially embryonic ones) and to differentiate into different types of cells, allows them to be used in regenerative medicine, in order to replace damaged tissues with degenerative lesions or diseases.

Due to the growing interest in stem cell applications, such as stem cell-based therapies for damaged organs, degenerative diseases¹ or reconstitution of the blood structure after chemotherapy in the treatment of leukemia,² a broad spectrum of methods has been developed to expand knowledge about the rules of this process. Several mathematical models were developed to aid in the understanding of stem cell differentiation.^3–7 The models involve different mathematical approaches to describe the processes of differentiation and self-renewal^7,8–10 that involve the proliferation of stem cells³ and the mechanisms of differentiation at each stage.⁴ All these models describe different parts of the homeostasis process in adult tissue. These models represent a first deterministic approach to mathematically understand this complex dynamic. Another important aspect in mathematical modeling is to incorporate those environmental and external disturbances into the system, which in the previous models are not considered, but which nonetheless positively or negatively influence the maturation and self-renewal process of the stem cells. This gives rise to stochastic models that, as a fundamental characteristic, consider the environmental disturbances of the system, which are expressed mathematically by means of diffusion coefficients and gaussian noise. These new factors considered has a direct impact on the modeling and representation of the cell maturation process. The development and study of this type of models expresses the existing interest in deepening knowledge in the applications that the area of ​​stochastic processes has to biology. Hence, in this investigation our scientific problem derives from the interpretation of this random noise in the process of cellular maturation.

The model is based on the assumption that the differentiation process is strictly related to cell division, that is, that differentiation takes place only during cell division, then the rate of cell differentiation is proportional to that of proliferation.

To quantitatively describe the self-renewal, the so-called self-renewal fraction is introduced, $a_i$ , which describes which fraction of progeny cells (offspring) is identical to the progenitor cells, were $i=1,\mathrm{...},n$  is the corresponding stage of the maturation process (this parameter can be interpreted as the probability that the daughter cell has the same properties as the stem cell). Furthermore, $p_i$  for $i=1,\mathrm{...},n-1$  is the population proliferation rate in stage $\begin{array}{l}i,{\mu }_i,\\ {\alpha }_i\\ \left(W_{1,t},\mathrm{...}{W}_{n,t}\right)\\ {c^{\prime }}_1>0\\ i-1\\ {\mu }_i=\cdots ={\mu }_{n-1}=0\\ {\mu }_n>0\\ a_1>\frac{1}{2}\\ a_1>a_i\\ i=2,\mathrm{...},n-1\\ n=6\end{array}$  for $i=1,\mathrm{...},n$  represents the death rate in stage i and $c_{i}t$  represent the population density in the corresponding stage on the time .

Then:

$\{\begin{array}{l}\frac{d{C}_1\left(t\right)}{dt}=f_1\left(s(t),C_1\left(t\right)\right)\\ \frac{d{C}_1\left(t\right)}{dt}=f_2\left(s(t),C_2\left(t\right)\right)+g_1\left(s(t),C_1\left(t\right)\right)\\ \frac{d{C}_n\left(t\right)}{dt}=f_n\left(s(t),C_n\left(t\right)\right)+g_{n-1}\left(s(t),C_{n-1}\left(t\right)\right)\end{array}$ , whit

$f_i\left(t\right)=2a_i-1\ast p_i\ast c_{i}t-d_i\ast c_{i}t,i<n$  describes the density of maturation in the stage i of all stem cells, $g_i\left(t\right)=2\left(1-a_{i-1}\right)\ast p_{i-1}\ast c_{i-1}t,1<i<n$ , describes the density of density of maturation from one stage i to another $i+1$ of all stem cells in the process and $fn\left(t\right)=-d_n\ast c_n\left(t\right)$ , this equation describes the density of death mature and stem cells.

It is assumed that the feedback signal depends on the concentration of mature cells and is given by

$s\equiv s\left(C_n\left(t\right)\right)=\frac{1}{1+k{c}_n\left(t\right)}$ , where 𝑘 is a positive constant

(This dependence can be justified using a quasi-stable state of approximation of the possible dynamics of cytokine molecules,⁹)

Considering different possible regulatory feedback mechanisms, different types of non-linearity are reached in the model equations. In particular in Fried W ⁹ 3 different regulatory mechanisms are proposed.

M1)$p_i=\frac{p_i}{1+k{c}_n\left(t\right)}$  and $a_i$ constant, (model 1 in(9))

M2) $p_i$  constant and $a_i(s)=\frac{a_{i,\max }}{1+k{c}_n\left(t\right)}$ , (model 2 in(9))

  (1)

M3) $p_i=\frac{p_i}{1+k{c}_n(t)}$  and $a_i(s)=\frac{a_{i,\max }}{1+k{c}_n(t)}$ , (model 3 in(9))

The cellular behavior at each stage of maturation is described by parameters of mortality rate, proliferation rate and a probability of differentiation. In addition, it is assumed that the system is regulated by a single cytosine in a manner similar to the production of red blood cells is controlled by erythropoietin^9–12 or the process of granulocyte specialization is by G-CSF (colony stimulating factor of granulocytes).^13–15

A special version of the model

Let s be the concentration of signaling molecules and assuming that both processes, proliferation and differentiation are regulated by the signal (regulatory mode $M_2$ , the following system of differential equations is obtained that describes the dynamics of n cell subpopulations:

$\begin{array}{l}\frac{d{c}_1}{dt}=(2a_1{s}_{k_1}(t)-1)p_1{c}_1(t)-{\mu }_1{c}_1(t)\\ \frac{d{c}_1}{dt}=(2a_2{s}_{k_1}(t)-1)p_2{c}_2(t)+2\left(1-a_1{s}_{k_1}(t)\right)c_1(t)-{\mu }_2{c}_2(t)\\ \frac{d{c}_n}{dt}=2\left(1-a_{n-1}{s}_{k_1}(t)\right)p_{n-1}{c}_{{}_{n-1}}(t)-{\mu }_n{c}_n(t)\end{array}$   (2)

The real fraction of the self-renewal at time t is then given by $a_i{s}_{k_1}(t)$  and defined as a fraction of the direct progeny of Cells in stage  that are in the same stage of differentiation as their parents. Additionally, it is assumed that:

$\begin{array}{l}t=[0,\infty )\\ c_{\left(i,o\right)}\ge 0fori=\mathrm{1...}n,\\ {\mu }_i=0fori=\mathrm{1...}n-1,\\ {\mu }_n>0,\\ p_i\ge 0fori=\mathrm{1...}n,\\ a_i\in \left[0,1\right]fori=\mathrm{1...}n\end{array}$   (3)

The mortality rate, proliferation rate and initial conditions are non-negative and the self-renewal fraction is between 0 and 1, which corresponds to different types of differentiation: symmetric self-renewal, symmetric differentiation and asymmetric divisions.

The model is based on the assumption that the cells divide at the rate $p_i$ , resulting in $p_i{c}_i(t)$  of the descending cells in a unit of time t and the stage $i=1,\mathrm{...},n$ . The $a_i$  fraction of the progeny cells remains in the same stage of differentiation as the stem cell, while the $1-a$  fraction of the offspring cells differs, that is, the transfers to the highest differentiation stage. In addition, cell death at the ${\mu }_i$  rate is modeled.

It is also not able that when the population of mature cells $c_n$  reaches some values, then the term $\left(2a_i{s}_{k1}\left(t\right)-1\right)p_i{c}_i\left(t\right)$  becomes negative and the number of the cells in stage i decreases. On the other hand, when the density of mature cells is low, then $\left(2a_i{s}_{k1}\left(t\right)-1\right)p_i{c}_i\left(t\right)$  is positive and the number of cells in stage i increases provided that the mortality rates are not too high. This shows how the dynamics of each subpopulation of cells depends on the level of mature cells.

Model (2) is well laid out, the solution exists and is unique for $t\in [0.\infty )$

And for the initial non-negative condition, the solution of the system (2) remains non-negative, which is demonstrated in Mackey.⁷ Assuming also that

$\begin{array}{l}{\mu }_1<(2a_1-1)p_1,\\ 0<2a_{{}_1}{p}_{{}_1}({\mu }_i+p_i)-2a{p}_i({\mu }_1+p_1),parai=2,\mathrm{...},n-1\end{array}$   (4)

it is shown that the system (2) has a single positive steady state.⁷ The first inequality establishes that there is a level of density of mature cells such that ${c^{\prime }}_1>0$ . In other words, the population of stem cells does not simply decrease and become extinct, but also replenishes itself. The second inequality of 4 says that the signal strength for the self-maintenance of the stem cell population is less than the concentration necessary at some stage of maturation i to keep the population without influx from stage $i-1$ . This implies that ${\mu }_i=\cdots ={\mu }_{n-1}=0$  and ${\mu }_n>0$ . So, we get that condition (4) is equivalent to

$a_1>\frac{1}{2}$   (5)

$a_1>a_i$  for $i=2,\mathrm{...},n-1$

The number $n=6$  considered in Lasota¹⁰ corresponds to hematopoietic stem cell maturation in different stages of the process: long-term repopulating stem cells, short-term repopulation stem cells, multipotent progenitor cells, compromised progenitor cells, precursors and mature cells.

Numerical solutions through the Mathematica package of the deterministic model with regulatory mode M2.

Case of six compartments (Hematopoietic Cell), represented by LT-HSC (long-term repopulation stem cells), ST-HSC (short-term repopulation stem cells), MPC (multipotent progenitor cells), CPC (compromised progenitor cells), precursor cells and stem cells, each type of cell represent a compartment (Figure 1):

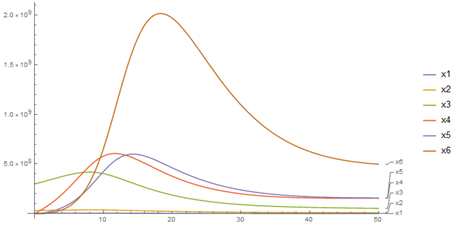
Figure 1 Case of six compartments for $a_1=0.7,a_2=0.65,a_3=0.65,a_4=0.65,a_5=0.55,p_1=0.8,p_2=0.11,p_3=0.17,p_4=0.34,p_5=0.69,\mu =0.3conk=1,2\ast {10}^{-9}$ , $c_1\left(0\right)={10}^5,c_2\left(0\right)={10}^6,c_3\left(0\right)={10}^7,c_4\left(0\right)=0,c_5\left(0\right)=0,c_6\left(0\right)=0$ and final time t = 50.

The parameters and initial conditions were taken from Pa´zdziorek Pl.¹⁶ In the deterministic model, an accelerated increase in the population of mature cells in the final stage is obtained during days 10 and 20, and between days 20 and 40 this number decreases, remaining stable for more than 40 days. Clinical data report an average recovery when the patient has more than 1.5 * 10 ^ 8 mature cells per liter of body blood, this system offers us an ideal vision of the result that may be in contrast to the actual data.

The stochastic model

We now present a stochastic version of the deterministic model (2). The last deterministic number of differential equations is transformed into a system of stochastic differential equations as follows:

$\begin{array}{l}d{\xi }_1=\left(\left(\frac{2a_1}{1+k{\xi }_n(t)}-1)\right)p_1{\xi }_1(t)-{\mu }_1{\xi }_1(t)\right)dt+{\alpha }_1{\xi }_1(t)d{W}_{1,t}\\ d{\xi }_2=\left(\left(\frac{2a_1}{1+k{\xi }_n(t)}-1)\right)p_2{\xi }_2(t)+2(1-\frac{a_1}{1+k{\xi }_n(t)})-{\mu }_1{\xi }_1(t)\right)dt+{\alpha }_1{\xi }_1(t)d{W}_{1,t}\\ d{\xi }_n=\left(2(1-\frac{a_{n-}{}_1}{1+k{\xi }_n(t)})p_{{}_{n-}}{}_{{}_1{\xi }_{{}_n-1}(t)-}{\mu }_n{\xi }_n(t)\right)dt+{\alpha }_n{\xi }_n(t)d{W}_{n,t}\end{array}$   (6)

Where the stochastic processes ${\xi }_1,{\xi }_2,\mathrm{..........},{\xi }_n$  describe the densities of the population of stem cells, cells at different stages of differentiation and mature cells. The coefficients $a_i,p_i$  for $i=1,\mathrm{...},n-1$  and ${\mu }_i$  for $i=1,\mathrm{...},n$  satisfy the assumptions (3), (4). $\left(W_{1,t},\mathrm{...}{W}_{n,t}\right)$  is a n-dimensional Wiener process and ${\alpha }_i$  for $i=1,\mathrm{...},n$  are positive.

Mathematical and biological justification of the stochastic system

This section shows the six-dimensional version (compartments) of the stochastic model of the stochastic system. For this, the noise term is maintained in each compartment and the population densities are treated as stochastic processes. The noise term is made up of the population density of the cell type of the indicated compartment, the Wiener process, independent of the rest of the processes and an $\alpha >0$ , which regulates the intensity of the Wiener process in each equation. That equations represent the population dynamics of the cells in the different stages of maturation. So that the smaller the system is closer to the deterministic model and as it increases, the greater the Wiener process has in the solution that is gets.

 The deterministic model is developed in an ideal environment, without influence of the external environment for the rates of self-renewal and proliferation. For the development of this investigation the term of noise is added. It is desired to reach conclusions on the influence of the environment during the process of cell division and maturation, applying different levels of stochastic noise intensity in each compartment. The process of cell division and maturation is represented as a Markov chain. So, it is necessary to use an independent Wiener process at each stage, since the population density of each compartment i at time t only depends on its own density in that same instant of time. In addition, the Wiener process is used because the model on cell division is raised from in vitro culture or in some type of fluid, which represents a Brownian movement with statistically independent and stationary increases.

In biological terms, this fluid produces different random stimuli, which together with the different feedback signals on the stem cells at each stage of the culture, can influence the speed of realization of the process of cell division and maturation and the density and quantity of cells, both of the first type (stem cells), and of the required final result (mature cells), at the end of the culture time in the applied environment.

6-dimensional model (hematopoietic cell)

The following section shows the six-compartment version of the general model on cell maturation presented in the previous section, which represents the cell cycle for hematopoietic stem cells. This is solved using the parameters used in the deterministic model proposed in⁹ with randomly selected noise levels, which include low and high levels compared to the models previously analyzed, because the intensity of the same can have different effects when vary the number of dimensions analyzed in the stochastic system. The model proposed for six dimensions is as follows:

$\begin{array}{l}d{\xi }_1\left[t\right]=\left(\left(\frac{2a_1}{1+k{\xi }_6\left[t\right]}\right)p_1{\xi }_1\left[t\right]\right)dt+{\alpha }_1{\xi }_1\left[t\right]d{w}_1\left[t\right]\\ d{\xi }_2\left[t\right]=\left(\left(\frac{2a_2}{1+k{\xi }_6\left[t\right]}-1\right)p_2{\xi }_2\left[t\right]+2\left(1-\frac{a_1}{1+k\ast {\xi }_6\left[t\right]}\right)p_1{\xi }_1\left[t\right]\right)dt+{\alpha }_2{\xi }_2\left[t\right]d{w}_2\left[t\right]\\ d{\xi }_3\left[t\right]=\left(\left(\frac{2a_3}{1+k{\xi }_6\left[t\right]}-1\right)p_3{\xi }_3\left[t\right]+2\left(1-\frac{a_2}{1+k\ast {\xi }_6\left[t\right]}\right)p_2{\xi }_2\left[t\right]\right)dt+{\alpha }_3{\xi }_3\left[t\right]d{w}_3\left[t\right]\\ d{\xi }_4\left[t\right]=\left(\left(\frac{2a_4}{1+k{\xi }_6\left[t\right]}-1\right)p_4{\xi }_4\left[t\right]+2\left(1-\frac{a_3}{1+k\ast {\xi }_6\left[t\right]}\right)p_3{\xi }_3\left[t\right]\right)dt+{\alpha }_4{\xi }_4\left[t\right]d{w}_4\left[t\right]\\ d{\xi }_5\left[t\right]=\left(\left(\frac{2a_5}{1+k{\xi }_6\left[t\right]}-1\right)p_5{\xi }_5\left[t\right]+2\left(1-\frac{a_4}{1+k\ast {\xi }_6\left[t\right]}\right)p_4{\xi }_4\left[t\right]\right)dt+{\alpha }_5{\xi }_5\left[t\right]d{w}_5\left[t\right]\\ d{\xi }_6\left[t\right]=\left(2\left(1-\frac{a_5}{1+k\ast {\xi }_6\left[t\right]}\right)p_5{\xi }_5\left[t\right]-\mu {\xi }_6\left[t\right]\right)dt+{\alpha }_6{\xi }_6\left[t\right]d{w}_6\left[t\right]\end{array}$   (12)

Evaluated for $a_1=0.51,a_2=a_3=a_4=0.475,a_5=0.41$ , $p_1=0.173,p_2=0.231,p_3=0.347,p_4=0.693,p_5=1.386$ , $\mu =0.3,k=1.28\ast {10}^{-9}$  and initials conditions ${\xi }_1\left(0\right)={10}^5,{\xi }_2\left(0\right)={10}^6,{\xi }_3\left(0\right)={10}^9,{\xi }_4={\xi }_5={\xi }_6=0$ , e noise intensities for ${\alpha }_1=0.011,{\alpha }_2=0.013,{\alpha }_3=0.015,{\alpha }_4=0.017,{\alpha }_5=0.019,{\alpha }_6=0.025$

Using the Euler–Maruyama method, an approximation of the Gillespie Algorism whit the functions of ItoProcess and RandomFunction of Mathematica software, to resolves the system, then is as follows (Figure 2):

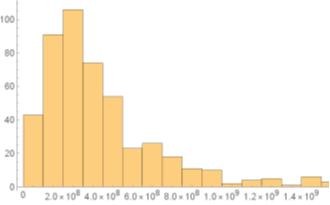
Figure 2 Histogram of 500 trajectories of the Six-dimensional model whit a t - final = 5 days, the same parameters to Figure 1.

The graph shows the results of 500 trajectories analyzing only the mature cell count using the stochastic SDE. For this, the same parameters are used as in the deterministic system and noise is added as a random real between 0 and 0.5 for each compartment during the 500 simulations. A simulation is performed with a final time of 50 days according to the final result of the deterministic model, where stability is reached. The implementation of this noise level is a little higher than what an average patient could present, so it is done by implementing the Gillespie Algorithm to give greater accuracy. It is observed how 91 trajectories are between 1.5 and $2.5\ast {10}^8$ , 106 are between 2.5 and $3.5\ast {10}^8$  and 74 between 3.5 and $4.5\ast {10}^8$  mature cells per liter of blood, coinciding with the clinical data taken from the bibliography and showing great accuracy due to the presence of the environmental noise factor during treatment. To verify that most of the trajectories are not null and are in the range obtained, the following representation was made (Figure 3):

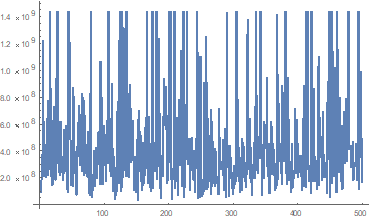
Figure 3 Represent the final results of the 500 trajectories employed in the solution of a stocastic model, using the leukocyte count on the y-axis and trajectory on the x-axis.

This graph shows the fluctuation of the final result of each trajectory, in which it is observable that practically none of them is null and are in the established range. A spontaneous approach is performed as a final verification resource that indicates how most of it focuses in the range of 2.0 to $4.0\ast {10}^8$  mature cells per liter of body blood.

The results of the numerical simulations of the stochastic and deterministic models show a contrast of results at the end of the cell maturation process, given for a generic patient complying with the parameters extracted from the literature.¹² There is a noticeable difference in results between the deterministic model and the stochastic system used.

The latter presents a cell maturation lower than the results shown by the deterministic model in a range of 0.5 to 3 * 10 ^ 8 cells per liter of blood. This results in an increase in the mortality of mature cells when passing from one state to the other and in the final stage of maturation. Taking into account the biological hypotheses for the maintenance of stability, this increase in mortality occurs in the last stage in a broad sense due to the appearance of external noise. In this case, the noise is expressed according to the patient's clinical state by means of a Brownian movement as explained above. Therefore, the presence of the stochastic component and the increase in its influence have a direct effect on the mortality of the culture cells, especially the last non-proliferative stages.

Mathematical models to describe the maturation of the hematopoietic stem cell can vary depending on the desired result. The deterministic model used allows obtaining an ideal and theoretical result of performing a bone marrow transplant with exact parameters and a representation of fluctuations without alteration internal or external to the culture. This in turn offers a theoretical initial approach to perform more detailed analyzes on the behavior of bone marrow transplantation. While the stochastic model gives a more realistic view of the cell maturation process, due to the introduction of stochastic noise that represents certain clinical states of the patient or external conditions during the process. It also presents greater fluctuation than the deterministic model and great variability of the final results.

These are grouped into a band that contains from the minimum results to the maximum allowed according to the stability theory applied to said model and the actual results of transplants performed. In this band, between 50 and 55% of the trajectories shown depending on the noise parameter are collected and have values ​​between 2.0 and 4.5 * 10 ^ 8 cells per liter, with a difference between 0.5 and 3 * 10 ^ 8 compared to the theoretical model. As a direct consequence of the stochastic model, there is an increase in mortality in the last stages of cultivation, depending on the intensity of the stochastic noise used. That is, the greater the influence of stochastic noise, the greater the mortality of mature cells during the process. Due to this, a random noise between 0 and 0.5 was used, which represents a path from the trend to the deterministic model to a slightly higher impact of deaths than the indicators shown by Pa´zdziorek Pl.^16,17–22

 The stochastic model shows greater similarity with the clinical data offered by doctors and the literature than the deterministic model, using its analysis as a starting point, to largely suppress extreme and inaccurate results. Said results can vary from extremely high noises that lead to an imbalance of the system or too close to the theoretical model that limits obtaining precise results and creates a false state of accuracy. In a broad sense, the stochastic model is superior in representation and possibilities of results to the deterministic one, but, due to the complexity of modeling the initial parameters, such as noise itself or the initial selection of a clinical recovery time, without taking into account empirical diagnoses from the collection of information from various cases treated, it is recommended to make an initial approach from the theoretical models.

None.

The authors declare no conflicts of interest.

1. Gratwohl A, Baldomero H. Trends of hematopoietic stem cell transplantation in the third millennium. Curr Opin Hematol. 2009;16(6):420–426.
2. Marciniak-Czochra A, Stiel T. Mathematical models of hematopoietic reconstruction after stem cell transplantation. Model Based Parameter Estimation. 2012;4:191–206.
3. Till JE, Mcculloch EA, Siminovitch L. A stochastic model of stem cell proliferation, based on the growth of spleen colony-forming cells: Proc Natl Acad Sci U S A. 1964;54(1):29–36.
4. Wu KL-P Z, Bugde A, Molyneux LA, et al. Capacity for stochastic self-renewal and differentiation in mammalian spermatogonial stem cells. J Cell Biol. 2009;187(4):513–524.
5. Stiehl V, A M-Czochra. Characterization of stem cells using mathematical models of multistage cell lineages. Mathematical and Computer Modelling. 2010;53(7–8):1505–1517.
6. Marciniak-Czochra A, Stiehl T, Jaeger W, et al. Modelling of asymmetric cell division in hematopoietic stem cells-regulation of self-renewal is essential for efficient repopulation. Stem Cells Dev. 2009;18(3):77–85.
7. Mackey MC, Colijn C. A mathematical model of hematopoiesis: I Periodic chronic myelogenous leukemia. J Theoret Biol. 2005;237(2):117–132.
8. Doumic M, AM-Czochra, Perthame B, et al. A Structured Population Model of Cell Differentiation. SIAM J Appl Math. 2011;71(6):1918–1940.
9. Fried W. Erythropoietin and erythropoiesis. Exp Hematol. 2009;37(9):1007–1015.
10. Lasota A, Mackey MC, Wazewska-Czyzewska M. Minimizing therapeutically induced anemia. J Math Biol. 1981;13:149–158.
11. Adamson JW. The relationship of erythropoietin and iron metabolism to red blood cell production in humans. Sem Oncol. 1994;21(2 suppl 3):9–15.
12. Ratajczak MZ, Ratajczak J, Marlicz W, et al. Recombinant human thrombopoietin (TPO) stimulates erythropoiesis by inhibiting erythroid progenitor cell apoptosis. Br J Haematol. 1997;98(1):8–17.
13. Metcalf D. Hematopoietic cytokines. Blood. 2008;111(2):485–491.
14. Semerad CL, Liu F, Gregory AD, et al. G-CSF Is an Essential Regulator of Neutrophil Trafficking from the Bone Marrow to the Blood. Immunity. 2002;17(4):413–423.
15. Price TH, Chatta GS,  Dale DC. Effect of recombinant granulocyte colony-stimulating factor on neutrophil kinetics in normal young and elderly humans. Blood. 1996;88(1):335–340.
16. Pa´zdziorek Pl. Mathematical model of stem cell. Preprint. 2012.
17. Rudnicki R. Long-time behaviour of a stochastic prey-predator model. Stochastic Processes and their Applications. 2003;108(1):93–107.
18. Ehnert S, Schmitt A, Vogt S, et al. The possible use of stem cells in regenerative: Langenbecks Arch Surg. 2009;394(6):985–997.
19. Pichor K, Rudnicki R. Stability of Markov semigroups and appplications to parabolic systems. J Math Anal Appl. 1997;215(11):56–74.
20. Rudnicki R, Pichor K, Tyran-Kaminska M. Lecture Notes in Physcics 597. Markov semigroups and their applications, Dynamics of Dissipation. 2002;597:215–38.
21. H JJ. Blood cell formation. In: Jandl JH, editor. Textbook of Hematology. Little. Boston: Brown and Company; 1996.
22. Wolfram Research.