Structures lying in close proximity experience multi-body dynamics, the impact phenomenon of which is known as pounding. This may lead to deck-unseating or in-plane deck rotation, phenomenon usually observed during high seismic activities. This leads to the important aspect of calculating the possibility of stick and slip to understand the safety of the design. The calculation is carried out by employing a linear complementarity in both the linear and tangential directions for observing the interaction between the two decks, which are considered to be rigid. The various conditions of the pre-impacting parameters, for all the possible stick-stick combinations, in the case of single impact are analytically determined. It is observed that the rotational potential of the deck, in-plane, is present for curved bridges having S-type configuration and needs to be considered while designing.

Keywords: multi-body dynamics, frictional impact, segmental curved bridges, linear complementarity problem, unilateral contact

The most used life-line structure of the modern day is the bridges, which has been developed significantly, with the most recent introduction being of the curved bridges. They provide an aesthetic look and are also very convenient at various crossings and cross-over. However, curved bridges have been observed to have poor seismic response. Pounding between the adjacent segments, in-plane deck rotation and deck abutment interaction make the curved bridges very susceptible during such activities, resulting in deck unseating, shear failure, torsional failure and the interfacial concrete failure.¹

San Fernando earthquake, in 1971, saw the first deck un-seating in the Golden state - Antelope Valley freeway interchange in California.^1,2 Many other devastations observed in the Loma Prieta earthquake, Northridge earthquake,^1,3 Chile earthquake,⁴ Christchurch earthquake^5‒7 and others brought out the necessity of making structures earthquake resistance, especially in the case of the curved bridges. The first experimental study, on curved bridges, was conducted in 2014 to observe and analysis the rotation of segmental curved bridges, the governing mechanics and the pounding failure patterns.^8,9 However, a proper thorough analytical analysis on the pounding of curved bridges is very limited; whereas, straight and skew bridges have a significant amount of studies in the current literature.^4,10‒20 Therefore, analysing the impact behaviour of the S-oriented curved bridges is a first and this study aims to fill a very important gap in the literature.

Compliance method forms the usual method used for modelling pounding mechanisms, simulating the entire phenomenon with contact elements, such as, damped springs (Kelvin elements)^21‒23 and non-linear springs (Hertz)^24‒26 considering impact to be centric and allowing penetration during contact. Other significant studies include the two-dimensional study by Andreaus et al.,²⁷ SDOF oscillator without friction²⁸ and considering friction^29,30 and observing the forced motion of a oscillator, having friction, which is limited by both rigid an deformable bodies.³¹ However, Chanda et al.,³² & Banerjee et al.,³³studied the behaviours of the various impact models and concluded that the unilateral contact is the most suited method in the field of non-smooth dynamics for calculating impact between two segments, because time-lag due to penetration will always take place in the case of compliance methods.^34‒37 Moreau³⁸ & Panagiotopoulos^39,40 first applied this method in the impact analysis, by transforming the inequality forms of the laws of impact. Following comprehensive works by Abbas et al.⁴¹ Glocker⁴² and others helped in the usual personification of the ideas of convex study and laws in the method of unilateral contact. Further studies by Leine et al.,⁴³ on simulated toy structures, such as, woodpecker, the tumbling toy and the waddling duck, have helped in establishing the method firmly into the field of impact analysis. Subsequently, Theodosiou et al.,⁴⁴ analysed the dynamic response involved in multiple unilateral contacts in the large scale, using finite element approach. Dimitrakopoulus¹⁰ then extended the work for observing the seismic behaviour experienced by skewed bridges, which is further extended in this study.

Newton’s impact and Coulomb’s frictional laws, are implemented to study the stick slip possibilities, due to the various pre-impact conditions, in curved bridges, in the normal and transverse directions respectively. The governing geometry greatly influences the post-impact deck responses, which is again dependent on the pre-impact conditions and this complex phenomenon is analytically studied for single impact conditions during deck-deck pounding of a curved bridge with two successive segments forming an , both the decks being rigid. All the possible cases of slip and stick, when the two furthest points of each deck are in contact with the other’s contour, are elucidated in Figure 1. The study helps to observe the safety conditions in constructing such bridges with future references for designers and analysists.

Figure 1 The classification of the entire frictional post-impact phenomenon.

Oblique unilateral frictional contact method is based on the Newton's impact law along the normal direction and the Coulomb's frictional law in the transverse or oblique direction.^45,46 Therefore, the coefficient of friction $\left(\mu \right)$ and the coefficient of restitution $\left({\epsilon }_N\right)$ constitute the two important parameters for simulating the frictional effect. Thus, the two laws are used to formulate a problem on the linear complementarity (LCP), which can depicted as $y=Ax+B$ , in which $A$ and $B$ are the known quantities, with the constraint $y^{T}x=0,\forall x,y\ge 0$ , and representing that either x or y is zero or else positive. The LCP is solved using the Lemke’s algorithm.^47,48 The ratio between the relative post-impact $\left({\gamma }_N^{+}\right)$ and pre-impact $\left({\gamma }_N^{-}\right)$ velocities is known as the coefficient of restitution $\left({\epsilon }_N\right)$ . It can be followed from the work of Banerjee et al.,⁴⁹ that based on these and using Newton’s Impact Law and Coulomb’s Frictional Law, with the range of the coefficient of restitution being ${\epsilon }_N\in [0,1]$ and assuming ${\epsilon }_T=0$ in the oblique direction, the linear complementarity equation, in a coupled set, is represented as:

$\left\{\begin{array}{c}{\upsilon }_N\\ {\gamma }_T^{+}\\ {\Lambda }_{TL}\end{array}\right\}=\left[\begin{array}{ccc}\left(G_{NN}-\mu G_{NT}\right)& G_{NT}& 0\\ \left(G_{TN}-\mu G_{TT}\right)& G_{TT}& I\\ 2\mu & -I& 0\end{array}\right]\left\{\begin{array}{c}{\Lambda }_N\\ {\Lambda }_{TR}\\ {\dot{g}}_T^{-}\end{array}\right\}+\left\{\begin{array}{c}\left(I+{\epsilon }_N\right){\gamma }_N^{-}\\ {\gamma }_T^{-}\\ 0\end{array}\right\}$ (1)

where, $\Lambda$ is the impulse, ${\upsilon }_N$ is the velocity jump, ${\gamma }_T^{\pm }$ is the relative velocity at post and pre-impact conditions in the transverse direction and $G_{xx}$ represents the effective mass for different conditions. Various states of impact, such as ‘stick’ and ‘slip’, for single impact as well as double impact, can be evaluated using the LCP formulation, illustrated in Eq. (1). The biggest advantage of the LCP method is the availability of all the elements in the form of matrices, instead of being in scalar quantities, as found in the Compliance Method. It should be noted that j represents the number of the deck $\left(1,2\right)$ and $k$ represents the inner or outer point $\left(i,o\right)$ of each deck. The widths of the decks $\left(W\right)$ are also considered to be equal and constant and so are the thicknesses $\left(t\right)$ .

The post-impact behaviour of the bridge segment is dependent mainly on the effective mass of impact $\left(G_{NN}\right)$ and the mass matrix $\left(M\right)$ . The other dependent parameters are estimated based on the pre-impact conditions and the different impacting orientations of the deck segment as illustrated in Figure 2. The decks are in contact at the lower parts of each and thus, only the distances of the lever arms are considered for the lower part of each. The considerable distances, the plan area, the centre of masses and the moments of inertia are calculated based on the similar formulations thoroughly elucidated in the work presented by Banerjee et al.⁴⁹ Therefore, the mass matrix is calculated to be:

$M=diag\left\{\begin{array}{cccccc}{m}_1& m_1& I_{m_1}& m_2& m_2& I_{m_2}\end{array}\right\}$ (2)

The lever arms are also calculated based on the same formulation for both the conditions of decks not rotating and the decks rotating about the centre of mass.

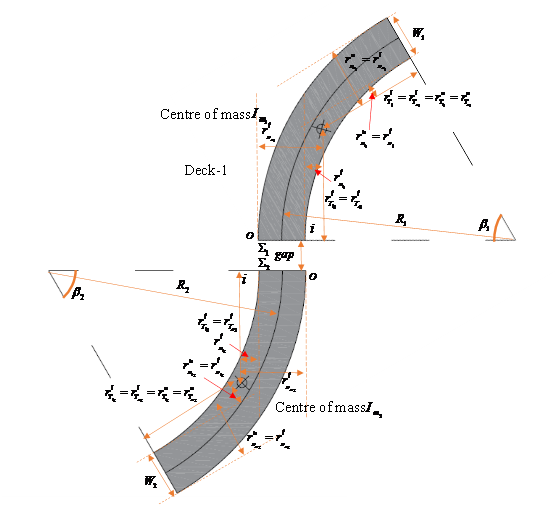
Figure 2 Deck geometry of the curved bridge showing the position of center of mass and the different impacting parameters without in-plane deck rotation.

Therefore, considering the rigid body rotation, the value of the lever arms change to:

$\begin{array}{l}{\tilde{r}}_{N_{i_j}}=r_{N_{i_j}}\cos {\theta }_j+r_{T_{i_j}}\sin {\theta }_j\\ {\tilde{r}}_{N_{o_j}}=r_{N_{o_j}}\cos {\theta }_j+r_{T_{o_j}}\sin {\theta }_j\\ {\tilde{r}}_{T_{i_1}}=-r_{N_{i_1}}\sin {\theta }_1+r_{T_{i_1}}\cos {\theta }_1\\ {\tilde{r}}_{T_{o_1}}=-r_{N_{o_1}}\sin {\theta }_1+r_{T_{o_1}}\cos {\theta }_1\\ {\tilde{r}}_{T_{i_2}}=r_{N_{i_2}}\sin {\theta }_2-r_{T_{i_2}}\cos {\theta }_2\\ {\tilde{r}}_{T_{o_2}}=r_{N_{o_2}}\sin {\theta }_2-r_{T_{o_2}}\cos {\theta }_2\end{array}$ (3)

where, ${\tilde{r}}_{N_{i_j}}\&{\tilde{r}}_{N_{o_j}}$ $\left(j=1,2\right)$ represent the distance from the centre of mass of the normal drawn on the inner and outer potential impacting points of the decks and ${\tilde{r}}_{T_{i_j}}\&{\tilde{r}}_{T_{o_j}}$ denote that of the transverse drawn on the same points.

The direction matrices for the two decks due to rotation by ${\theta }_1\&{\theta }_2$ angles respectively are derived and the normal and tangential distances of the centre of mass are deduced as:

$\left\{\begin{array}{l}{\tilde{r}}_{N_{{\theta }_{j_{k_{\widehat{j}}}}}}\\ {\tilde{r}}_{T_{{\theta }_{j_{k_{\widehat{j}}}}}}\end{array}\right\}=\left[\begin{array}{cc}\cos {\theta }_j& -\sin {\theta }_j\\ \sin {\theta }_j& \cos {\theta }_j\end{array}\right]\left\{\begin{array}{c}{\tilde{r}}_{N_{k_{\widehat{j}}}}\\ {\tilde{r}}_{T_{k_{\widehat{j}}}}\end{array}\right\}$ (4)

where, $\widehat{j}$ is complementary to $j$ , which means $j=1\to \widehat{j}=2$ and vice versa. The direction matrix helps to calculate the relation between the relative velocities between the two points of impact, with respect to the relative velocities between the two decks.

Therefore, the normal $\left(W_{N_1}\right)$ and transverse $\left(W_{T_1}\right)$ directional matrices, when deck-1 is in impact at the contour $({\sigma }_2)$ of deck-2 are:

$\begin{array}{l}{W}_{N_{k_1}}={\left\{\begin{array}{cccccc}-\sin {\theta }_2& \cos {\theta }_2& {\tilde{r}}_{N_{{\theta }_{2_{k_1}}}}& \sin {\theta }_2& -\cos {\theta }_2& {\tilde{r}}_{N_{{\sigma }_2}}\end{array}\right\}}^T\\ W_{T_{k_1}}={\left\{\begin{array}{cccccc}\cos {\theta }_2& \sin {\theta }_2& {\tilde{r}}_{T_{{\theta }_{2_{k_1}}}}& -\cos {\theta }_2& -\sin {\theta }_2& {\tilde{r}}_{T_{{\sigma }_2}}\end{array}\right\}}^T\end{array}$ (5)

In the same way, the direction matrices when deck-2 is in impact with that of the contour $({\sigma }_1)$ of deck-1 are:

$\begin{array}{l}{W}_{N_{k_2}}={\left\{\begin{array}{cccccc}-\sin {\theta }_1& \cos {\theta }_1& {\tilde{r}}_{N_{{\sigma }_1}}& \sin {\theta }_1& -\cos {\theta }_1& {\tilde{r}}_{N_{{\theta }_{1_{k_2}}}}\end{array}\right\}}^T\\ W_{T_{k_2}}=\left\{\begin{array}{cccccc}\cos {\theta }_1& \sin {\theta }_1& {\tilde{r}}_{T_{{\sigma }_1}}& -\cos {\theta }_1& -\sin {\theta }_1& {\tilde{r}}_{T_{{\theta }_{1_{k_2}}}}\end{array}\right\}{\theta }_1^T\end{array}$ (6)

In Eqs. (5) and (6), the respective directional distances of the impacting points from the centre of masses are represented as ${\tilde{r}}_{N_{{\sigma }_1}}\&{\tilde{r}}_{T_{{\sigma }_1}}$ and ${\tilde{r}}_{N_{{\sigma }_2}}\&{\tilde{r}}_{T_{{\sigma }_2}}$ respectively.

Similarly, following the work done by Banerjee et al.,⁴⁹ on single segment curved bridges, the distance vector, $r_D$ , is calculated as:

$r_D=\left(\begin{array}{l}{r}_{N_{i_2}}-r_{N_{i_1}}+x_2-x_1+{\tilde{r}}_{N_{{\sigma }_1}}-{\tilde{r}}_{N_{{\sigma }_2}}\\ Y_{m_1}+Y_{m_2}+g-{\tilde{r}}_{T_{{\sigma }_1}}-{\tilde{r}}_{T_{{\sigma }_2}}+y_1-y_2\\ 0\end{array}\right)$ (7)

Therefore, with respect to the contours of impact, the normal and tangential coefficients of the distance vector, after the decks rotated by ${\theta }_1\&{\theta }_2$ respectively, are:

$\begin{array}{l}{n}_1=\left(\begin{array}{c}\sin {\theta }_1\\ -\cos {\theta }_1\\ 0\end{array}\right)\&t_1=\left(\begin{array}{c}\cos {\theta }_1\\ \sin {\theta }_1\\ 0\end{array}\right)\\ n_2=\left(\begin{array}{c}-\sin {\theta }_2\\ \cos {\theta }_2\\ 0\end{array}\right)\&t_2=\left(\begin{array}{c}-\cos {\theta }_2\\ -\sin {\theta }_2\\ 0\end{array}\right)\end{array}$ (8)

The respective impact points are thus calculated by considering the two instances separately. The first instance is the inner and outer edges of the deck-2 interacting with ${\sigma }_1$ , an unknown point on contour of deck-1, and the second being the exact thing occurring for deck-1. The unknown points are calculated as:

$\begin{array}{l}{\sigma }_1=R_1-X_{m_1}+\left(R_2+{\sigma }_2-X_{m_2}\right)\cos \left({\theta }_1-{\theta }_2\right)-Y_{m_2}\sin \left({\theta }_1+{\theta }_2\right)+\\ \left(r_{N_{i_2}}-r_{N_{i_1}}+x_2-x_1\right)\cos {\theta }_1+\left(Y_{m_1}+Y_{m_2}+g+y_1-y_2\right)\sin {\theta }_1\end{array}$ (9)

Similarly, it is also derived that:

$\begin{array}{l}{\sigma }_2=-R_2+X_{m_2}+\left(R_1+{\sigma }_1-X_{m_1}\right)\cos \left({\theta }_1-{\theta }_2\right)+Y_{m_1}\sin \left({\theta }_1-{\theta }_2\right)-2Y_{m_2}\sin {\theta }_2\cos {\theta }_2+\\ \left(r_{N_{i_2}}-r_{N_{i_1}}+x_2-x_1\right)\cos {\theta }_2+\left(Y_{m_1}+Y_{m_2}+g+y_1-y_2\right)\sin {\theta }_2\end{array}$ (10)

The exact values of ${\sigma }_1\&{\sigma }_2$ is calculated from the Eqs. (9) and (10) by considering:

$-\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\le {\sigma }_{\widehat{j}}\le \raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ (11)

The value of ${\sigma }_{\widehat{j}}=-\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ is considered when the inner point of deck-2 is in contact and ${\sigma }_{\widehat{j}}=\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ when the impact occurs on the outer point.

The gap, when deck-2 is in impact, is calculated from the vector equation, $r_D^T{n}_j=g_{N_j}$ , as:

$\begin{array}{l}g=2{\sigma }_1\tan {\theta }_1+\left(r_{N_{i_2}}-r_{N_{i_1}}+x_2-x_1\right)\tan {\theta }_1+\frac{Y_{m_1}}{\cos {\theta }_1}-\left(R_2+{\sigma }_2-X_{m_2}\right)\left(\tan {\theta }_1\cos {\theta }_2-\sin {\theta }_2\right)\\ \text{}\text{}+Y_{m_2}\left(\cos {\theta }_2-\tan {\theta }_1\sin {\theta }_2\right)-\left(Y_{m_1}+Y_{m_2}+y_1-y_2\right)\end{array}$ (12)

On the contrary, the gap, when deck-1 is in impact, is also calculated as:

$\begin{array}{l}g=2{\sigma }_1\tan {\theta }_2+\left(r_{N_{i_2}}-r_{N_{i_1}}+x_2-x_1\right)\tan {\theta }_2+\left(R_1-{\sigma }_1-X_{m_1}\right)\left(\tan {\theta }_2\cos {\theta }_1-\sin {\theta }_1\right)-\\ Y_{m_1}\left(\cos {\theta }_1+\sin {\theta }_1\tan {\theta }_2\right)-Y_{m_2}\left(\tan {\theta }_2\sin {\theta }_2-\cos {\theta }_2\right)-\left(Y_{m_1}+Y_{m_2}+y_1-y_2\right)\end{array}$ (13)

The possible impacting points can be observed from Figure 2, only considering in-plane deck-rotation. The stick-slip calculations are carried out with respect to the coordinate system of deck-2. The various conditions, during impact, as illustrated in Figure 1, are used to calculate the ratio between the pre-impact velocities, the most important pre-impact parameter to be considered by the designers during the design phase. The stick-slip occurrence, at the instance of impact, is significantly affected by the ratio of oblique and normal pre-impact velocities $\left(\raisebox{1ex}{${\gamma }_T^{-}$}\!\left/ \!\raisebox{-1ex}{${\gamma }_N^{-}$}\right.\right)$ and by the geometrical parameters of the deck, such as, the decks’ curved angles $\left({\beta }_1\&{\beta }_2\right)$ , the radii of the two decks $\left(R_1\&R_2\right)$ and the angles of rotation $\left({\theta }_1\&{\theta }_2\right)$ experienced by the decks. Thus, the pre-impact velocities are calculated, based on the directional matrices calculated from Eqs. (2,5,6) for each case of single impact, following the same trend as presented in the work presented by Banerjee et al.⁴⁹ It is observed that, the variation of the entire phenomenon of single impact is based on a single parameter, coined $\partial$ , with the width $\left(W\right)$ of both the decks being 10 meters. The entire parametric analysis is carried out based on the variations in the values of the curve angles $\left({60}^{\circ },{90}^{\circ },{120}^{\circ }\right)$ , radii of each bridge (100 meters and 200 meters), values of the coefficient of friction (0.5 and 1) and the value of the coefficient of restitution in the normal direction $\left({\epsilon }_N\right)$ being 0.5 for all the cases.

The phenomenon, when one of the four potential impacting points comes into contact with the surface of the other deck at ${\sigma }_j$ , is known as single impact. This occurs due to the pre-impact angular velocity experienced due to the deck rotation. When frictional impact is considered, the body starts slipping, when the resisting frictional force is surpassed, which may result in the un-seating of the deck due to the amplified in-plane deck rotation. Graphs are plotted based on the pre-impact velocity ratios observed for each case.

The parametric analysis, illustrated in Figure 3-6, is conducted on the curved deck geometries for different curved angles of 60⁰ and 90⁰ for the two decks, each having two radii of 100 meters and 200 meters. Figure 3 & 4 represent how the variation in sticking and slipping regions take place for 2 sets of $\beta$ values when both the inner and outer points are in contact with the surface of the other deck. The increase in stick region is obvious with the increase in the coefficient of friction, as more force is required to overcome it. When deck-2 is in impact with the contour of deck-1, the stick region gradually increases for both inward and outward slip, when the inner point is in contact; whereas, an opposite trend is observed when the outer point is in contact.

Figure 3 Illustration of the parametric study of the curved decks having 2 sets of  values and with ${\beta }_1={\beta }_2={60}^{\circ }$ , when compared between the two cases of impact, namely, deck-1 is in impact with deck-2 and vice-versa, for different coefficients of friction.

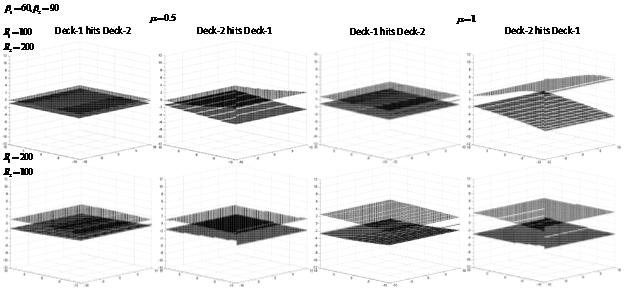
Figure 4 Illustration of the parametric study of the curved decks having 2 sets of  values and with ${\beta }_1={60}^0\&{\beta }_2={90}^0$ , between the two cases of impact, namely, deck-1 is in impact with deck-2 and vice-versa, for different coefficients of friction.

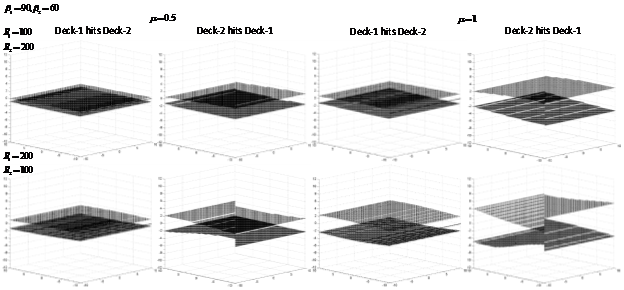
Figure 5 Illustration of the parametric study of the curved decks having 2 sets of $R_j$ values and with ${\beta }_1={90}^0\&{\beta }_2={60}^0$ , between the two cases of impact, namely, deck-1 is in impact with deck-2 and vice-versa, for different coefficients of friction.

Figure 6 Illustration of the parametric study of the curved decks having 2 sets of $R_j$ values and with ${\beta }_1={90}^0\&{\beta }_2={90}^0$ , between the two cases of impact, namely, deck-1 is in impact with deck-2 and vice-versa, for different coefficients of friction.

A unique feature is observed at the instance of deck-1 hitting deck-2, when the radius of deck-1 is 200m and that of deck-2 is 100m, where the amount stick region is more when the inner point of deck-1 is in contact and gradually decreases when the outer point is in impact.

Figure 5 & 6 elucidates that the variation in sticking and slipping regions for 2 other sets of $\beta$ values respectively, when either the inner or the outer points are in impact. The variation between the deck-1 hitting the surface of deck-2 and deck-2 hitting the surface of deck-1 are shown and it can again be observed that the increase in friction also results in the increase of the sticking region.

Maximum linear stick is again observed when the deck-1 is in contact with the contour of deck-2 and the frictional coefficient is 0.5. Variations in the stick regions can be observed with the amount of stick region being more when the inner point of deck-2 is in contact with the contour of deck-1.

The upper and lower planes, in Figure 3-6 represent the region of sticking with varying ratios of tangential and normal post-impact velocities in the z-axis, pre-impact rotation of deck-2 along the y-axis and that of deck-1 along the x-axis. -10 to 10 is considered to be the range of rotation of both the decks; whereas, -12 to 12 is taken in the range of $\raisebox{1ex}{${\gamma }_T^{-}$}\!\left/ \!\raisebox{-1ex}{${\gamma }_N^{-}$}\right.$ . The portions in graphs, above and below the sticking region, represent the various slipping conditions, namely, the inner point inward and outward slip and the outer point inward and outward slip for each deck.

These conditions are classified based on the thorough analytical concepts elaborated in the previous sections. The classification of the stick and slip regions, as represented by the graphs provided for studying the phenomenon of single impact, are explained in details in Figure 7 & 8.

Figure 7 The different post-impact phenomenon, depicted by the graphs when both the inner and outer points of deck-1 is in contact with the contour of deck-2, during single impact.

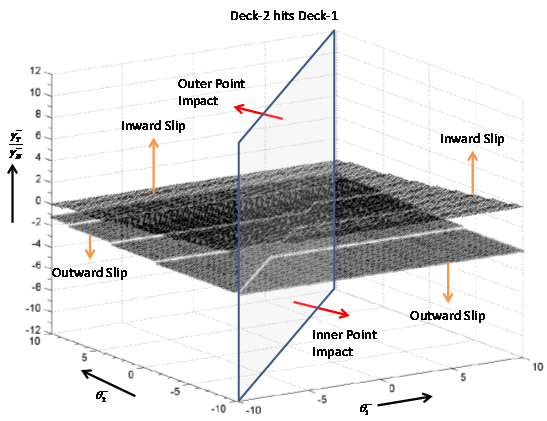
Figure 8 The different post-impact phenomenon, depicted by the graphs when both the inner and outer points of deck-2 is in contact with the contour of deck-1, during single impact.

The regions of inward and outward slip along with the representation of the specific point of impact, when the inner or outer point of deck-1 is in impact with the contour of deck-2, are elucidated in Figure 7. The inner-point impact occurs when deck-2 rotates in the positive direction; whereas, the impact is experienced at the outer point when deck-1 rotates in the positive direction. An opposite trend in the direction of inner point impact and outer point impact can be observed when single impact phenomenon is experienced by deck-2 on the contour of deck-1. The impact on the inner point is experienced when deck-1 rotates in the positive direction and that on the outer point is experienced when deck-2 rotates in the positive direction, the graphical representation of which is given in Figure 8.

It is known that the value of ${\gamma }_{N_{k_j}}^{-}$ is always negative and for the existence of outward slip the value of ${\gamma }_{T_{k_j}}^{-}$ should be positive. Thus, the ratio between ${\gamma }_{T_{k_j}}^{-}/{\gamma }_{N_{k_j}}^{-}$ is always negative (<0) and therefore the direction of the outward slip is represented by the lower part (negative region) of the ${\gamma }_T^{-}/{\gamma }_N^{-}$ axis, for both the cases. Similarly, the value of ${\gamma }_{T_{k_j}}^{-}$ is always negative which results in the representation of the inward slip on the upper part (positive side) of the ${\gamma }_T^{-}/{\gamma }_N^{-}$ axis. A comparatively linear variation, between the outward and inward slip, for both inner and outer point impacts is observed for all the cases, when the radii of both the decks are equal. The post-impact phenomenon is predictable and no abrupt variation is observed when the decks have equal radii, thus making the designs relatively convenient and safer. With $R_1>R_2$ , the region of sticking is observed to be higher when the inner point of deck-1 is in contact with the contour of deck-2, when the inner point of deck-2 is in contact with the contour of deck-1 and the coefficient of friction is 0.5 and when the outer point of deck-2 experiences impact with the contour of deck-1 and the coefficient of friction is 1.

On the other hand, with $R_1<R_2$ , the amount of stick is linear for both the points of impact when deck-1 experiences contact with deck-2 and the coefficient of friction is 0.5 and the region of stick is higher when the outer point of deck-1 hits deck-2 and the coefficient of friction is 1 and when the inner point of deck-2 hits deck-1 with both the coefficients of friction. Moreover, the tendency of outward slip is observed to be higher in general when deck-1 is in contact with deck-2 for all the variations of the radii; although, quite a few cases, with the coefficient of friction being unity, have almost proportional amount of outward and inward slip. In the case of the impacting points of deck-2 coming in contact with the contour of deck-1, the tendency of outward slip is higher at the instance of the outer point being in contact and that of the inward slip is higher at the instance of the inner point being in contact, when $R_1<R_2$ and also when $R_1>R_2$ and the coefficient of friction is 1. On the contrary, when the coefficient of friction is 0.5 and $R_1>R_2$ the tendency of inward slip is higher at the instance of the outer point of deck-2 being in contact with the contour of deck-1 and the outward slip is more when the inner point of deck-2 is in contact. The frictionless cases will be accompanied by only outward and inward slip, with a single demarcating plane along the axis, for describing the regions of the two slips (Table 1).

Curved bridges with two successive rigid abutments, with S-type orientation, and their post-impact effects due to in-deck rotation are investigated in the present work. The rotational mechanics involved in the in-deck interaction, for curved bridges, have not been theoretically studied in the past and this paper illustrates a thorough non-smooth event based parametric analysis for identifying the possibility of stick and slip, after impact. The post-impact rotational potential is observed to depend on the total angle of the curve, the ratio of the pre-impact relative velocities in the tangential and normal directions and the coefficient of friction. Specifically, the post-impact slip and stick phenomenon, during single impact, in dependent entirely on the value of $\partial$ and the main focus of the designers should lie on this and its related parameters. The validity of inward slip is negligible when the coefficient of friction is greater than 0.25. Thus, it can be inferred that the slipping tendency of curved bridges, during single impact, is considerably high and is an aspect which needs to be reduced in order to increase the safety of the structure.

None.

Author declares that there is no conflict of interest.