eISSN: 2641-936X

Electrical & Electronic Technology Open Access Journal

Correspondence:

Received: January 01, 1970 | Published: ,

Citation: DOI:

Download PDF

Abstract

One of the unaddressed and open challenges in the nano-networking is the characterstics of noise. The previous analysis, however, have concentrated on end-to-end communication model with no separate modelings for propagation channel and noise. By considering a separate signal propagation and noise model, the design and implementation of an optimum receiver will be much easier. In this paper we justify consideration of a separate additive Gaussian noise model of a nano-communication system based on the molecular communication channel for which are applicable for Msk and Mosk modulation schemes. The presented noise analysis is based on the Brownian motion process and advection molecular statistics, where the received random signal has a probability density function whose mean is equal to the mean number of the received molecules. Finally, the justification of received signal magnitude being uncorrelated with additive non-stationary white noise, is provided.

Keywords: molecular, noise, diffusion, channel, frequency shift keying

Introduction

Any molecular communication model similar to conventional digital communication system consist of three main components, they are the transmitter, receiver, and the channel. Figure 1 illustrates a schematic of a molecular communication model. In comparison with the digital communication system model, molecular communication system can also be implemented using different types of modulation schemes. The modulation techniques mainly used in digital communications.¹Pulse Amplitude Modulation (PAM), Phase Shift Keying (PSK), and Frequency Shift Keying (FSK). In PAM, different amplitudes are used for message modulation. In PSK, to modulate different messages finite number of phases are used, and in FSK, finite number of frequencies are used for modulating the messages.

Figure 1 A schematic of a molecular communication system.

Considering nano-communication transmission and reception environment as shown in Figure 2 in general, transmitters can employ three modulation techniques:

Concentration Shift Keying (CSK), which is similar to PAM. In this type of modulation, only one type of molecule is used and messages are encoded by different amounts of released molecules.^2–5

Pulse Position Modulation (PPM), where only on type of molecule is used and messages are encoded by transmitting single pulse in different time shifts.^6,7

Molecular Shift Keying (MOSK), in which messages are encoded by using different type of molecules.^8,9To avoid interference the signal space will be chosen to be orthogonal. In¹⁰ it is shown that this type of modulation in comparison to CSK is more robust against noise.

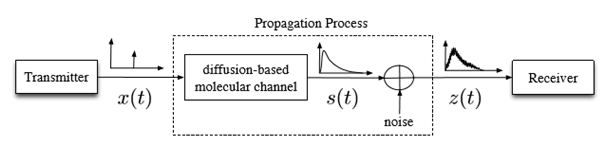
Figure 2 Block diagram of a molecular communication system.

The modeling and characterization of noise in a conventional communication is well defined and very broadly analyzed. But in contrast to this, in the molecular communications characterization of noise still one of the open challenges for researchers. Even though, noise sources of molecular communications are analyzed in terms of stochastic process, but most of the works have concentrated on a general end-to-end communication model with considering no separate model for the propagation channel and noise. It is then believed that, by having a separate signal propagation and noise model, if one wants to follow, the design of an optimum receiver will be much easier task.

Noise modeling in diffusion-based molecular communication

Consider the diffusion –based noisy channel of Figure 3; where at time zero ,Q number of messenger molecules are propagated through the diffusion channel of impulse response h(t). Let n(t) be the sample function of a noise random process N(t) , then due to the nature of the channel ,that is the diffusion channel ,it is not hard to see that we may be able to consider two different types of noises .That is n_b(t) and n_r(t) are being the Brownian and Residual noises respectively (Figure 4).

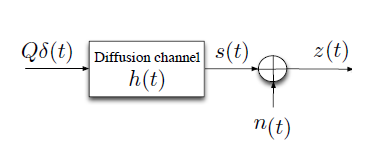
Figure 3 Diffusion-based molecular channel model.

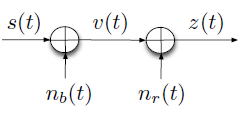
Figure 4 Model of the two separate noise components.

It is worth to know that, n_b(t) ,the Brownian noise is associated with the random thermal motion of the messenger molecules and n_r(t), the residual noise ,is as a result of the interference due to the messenger molecules. We also should remind that n_r(t) is analogous to the inter–symbol interferences in the conventional communications. Now, considering z(t) being the input to the receiver or the output of the channel, we might be able to write

Z(t)= s(t)+ n_b(t)+ n_r(t) (1)

Where s(t) is the mean number of the received messenger molecules.

Brownian noise in diffusion-based molecular channel

Since Brownian noise is produced by the random thermal motion of the transmitted messenger molecules, then the number of counted molecules at the receiver are random. Let X(t) = (x(t),y(t),z(t)) be a three dimensional position of a messenger molecule at time, t, since the Brownian motion is modeled by the Wiener process, for a two dimensional reception surface, we may write,

$\begin{array}{l} x (t) = \overset{\land}{x} + \sqrt{2 D t} u (t) \\ y (t) = \overset{\land}{y} + \sqrt{2 D t} u (t) \end{array}$ (2)

where (x,y) being the original position of the transmitted messenger molecular with u(t) having a standarized normal distribution, u(t) ~ N(0,1). Therefore, for, any fixed t=t₀, the mean or expected values of x(t₀) and y(t₀ ) are given respectively by ;

$\begin{array}{l} E (x (t_{0})) = \overset{\land}{x} + \sqrt{2 D t_{0}} E (U (t_{0})) = \overset{\land}{x} \\ E (y (t_{0})) = \overset{\land}{y} + \sqrt{2 D t_{0}} E (U (t_{0})) = \overset{\land}{y} \end{array}$ (3)

and as a result, for each emitted molecule ,the joint probability density function of being at point (x(t),y(t)), P_xy (x(t),y(t)) is a two dimensional Guassian distribution function , where

$P_{x y} (x (t), y (t)) = P_{x} (x (t)) P_{y} (y (t)) = \frac{1}{4 π D t} \exp (- \frac{{(x (t) - \overset{\land}{x})}^{2} + {(y (t) - \overset{\land}{y})}^{2}}{4 D t})$ (4)

with mean ( x^(t),y^{^}(t) ) and variance 2Dt, with D being the diffusion coefficient. Hence the probability of having a messenger molecule in the sensing surface area of A_r is given by:

$P = \iint_{A_{r}} P_{x y} (x (t), y (t)) d x d y = \iint_{A_{r}} \frac{1}{4 π D t} \exp (- \frac{{(x (t) - \overset{\land}{x})}^{2} + {(y (t) - \overset{\land}{y})}^{2}}{4 D t}) d x d y$ (5)

Let us now, assume that Q messenger molecules are emitted by the transmitter of the nano-system , then the reception of K messenger molecules in the sensing area of the receiver has Binomial distribution with probability mass function given by:

$P (k) = (\begin{array}{l} Q \\ k \end{array}) (\begin{array}{l} k \\ P \end{array}) {(1 - P)}^{Q - k}$ (6)

As we know, if we choose Q large and p small enough ,then the Eq.(6),can be approximated by a Gaussian distribution $N (μ, σ^{2})$ where $μ = Q P$ and $σ^{2} = Q P (1 - P)$ . By combining of the Eqs.(5 ,6 ) , we get the result

$μ = Q P = Q \iint_{A_{r}} \frac{1}{4 π D t} \exp (- \frac{{(x (t) - \overset{\land}{x})}^{2} + {(y (t) - \overset{\land}{y})}^{2}}{4 D t}) d x d y$ (7)

Comparing the mean value u in the Eq.(7) with the Eq.(5) ,it is not hard to see that these two quantities are the same ,that is u is the same as the mean number of received messenger molecules . This implies that the received random signal has a probability density function whose mean is the deterministic signal of the Eq.(5).Thus this equality justifies the facts that first, Brownian noise is additive, second signal in Eq.(5) is the response of the molecular channel. Let v(t) be the number of the messenger molecules corrupted by Brownian noise , as shown in Figure 5, to be defined as follows;

$v (t) = s (t) + n_{b} (t)$ (8)

then, v(t) has Gaussian distribution of mean s(t) and variance QP(1-P), that is N(s(t),QP(1-P)). So, v(t)-s(t)=n_b₍(t) has distribution of N(0,p(1-p)). Now if we assume p<<1, then we can say that 1-p~1 and only then the $var (n_{b}) = σ^{2}_{n b} \approx Q P$ . We also Know that QP=E(S(t)) and thus $n_{b} (t) = (\sqrt{s (t)}) N (0, 1)$ , which implies that Brownian noise follows a zero mean Gaussian process with variance equal to the mean number of received molecules in the sensing area. To investigate the statistical properties of the Brownian noise we want to compute the autocorrelation function of the Brownian noise, that is R_nb(t₁,t₂). Since the probability density function of the Brownian noise is derived through the probability density function of v(t), lets compute the second order density function of v(t). Using the chain rule of probability,

$P_{V} (v_{1}, v_{2}) = P (v_{2} | v_{1}) P (v_{1}) = P (v_{1} | v_{2}) P (v_{2})$ (9)

with v_i=v(t_i) for i=1,2. According to Eq.(6) v_i is a binomial random variable with parameters Q,P, B(Q,P) , with p₁ being the probability of Q messenger molecules at the receiving area at time t₁. The same argument is true for the v(t₂)=v₂. But p(V₂/V₁) ,the probability of having v₂ molecules at the receiving area at time t₂ given that v₁ molecules have been transmitted at time t₁ where t₁<t₂, we then can write.

$\begin{array}{l} P_{V} (v_{2} | v_{1}) = \sum_{i = 0}^{v_{1}} (i n u m b e r o f v_{1} m o l e c u l e s a r e s t a y i n g i n t h e s e n s e i n g a r e a) P (v_{2} - i n e w m o l e c u l e s a r e c o \min g) \\ = \sum_{i = 0}^{v_{1}} P_{s t} (i) P_{n a} (i) \end{array}$ (10)

where p_st(i) =p( i number of v₁ molecules staying in the sensing area) and is given by

$P_{s t} (i) = (\begin{array}{l} v_{1} \\ i \end{array}) (\begin{array}{l} i \\ p_{2} \end{array}) {(1 - p_{2})}^{v_{1} - i}$ (11)

where p₂_, being the probability of an event a messenger molecule staying in the receiving area after t₂ –t₁ seconds passed. Also, if we let p(v₂ –i new molecules are arriving ) =p_na(t), then

$P_{n a} (i) = (\begin{array}{l} Q - v_{1} \\ v_{2} - i \end{array}) (\begin{array}{l} v_{2} - i \\ p_{3} \end{array}) {(1 - p_{3})}^{(Q - v_{1}) - (v_{2} - i)}$ (12)

which is a binomial probability function , with p₃ being the probability of having a messenger molecule at the sensing area at time t₂. Now by considering the fact that for Q>>v₁ , then Q-V₁~ Q, we can write.

$P_{n a} (i) = (\begin{array}{l} Q \\ v_{2} - i \end{array}) (\begin{array}{l} v_{2} - i \\ p_{3} \end{array}) {(1 - p_{3})}^{Q - (v_{2} - i)}$ (13)

By assuming the remaining i molecules in the sensing area is negligible, that is i=0 , the Eq.(7) will become

$P (v_{2} | v_{1}) ≃ P_{n a} (i = 0) = (\begin{array}{l} Q \\ v_{2} \end{array}) (\begin{array}{l} v_{2} \\ p_{3} \end{array}) {(1 - p_{3})}^{Q - v_{2}} = P v (v_{2})$ (14)

for which we conclude that v₁ ,v₂, are two independent random variables, that implies the uncorrelatedness of the process v(t). By using Eq.(8 ) and Eq.(14) , and noting the fact that s(t) is a deterministic signal, we can coclude that n_b(t) is also uncorrelated white process;

$n_{b} (t) = (\sqrt{s (t)}) w (t)$ (15)

with w(t) being white Gaussian with mean zero and variance one, N(0,1). Now if we let the autocorrelation function of the Brownian noise, n_b(t), be R_nb(t₂,t₁), then

$R_{n b} (t_{2}, t_{1}) = E (n_{b} (t_{1}) n_{b} (t_{2})) = \sqrt{s (t_{1}) s (t_{2})} E (w (t_{1}) w (t_{2})) = \sqrt{s (t_{1}) s (t_{2})} δ (t_{1} - t_{2})$ (16)

In addition to that, since the variance of the Brownian noise is

$σ^{2}_{n b} (t) = E {(n_{n b} (t) - E (n_{n b} (t)))}^{2} = R_{n b} (t, t) - (E {(n_{b} (t))}^{2} = s (t)$ (17)

which constantly changes with time, we then conclude that it is also a non-stationary noise.

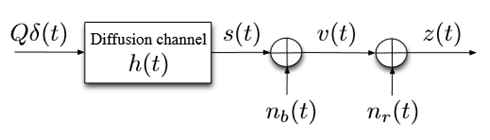
Figure 5 Diffusion-based molecular channel model.

Residual noise in diffussion-based molecular channel

The chemical receptors may contain residual molecules on the surface of the nano machine structure from the previous reception the same time there may also be molecules from the current communication symbol, thus distortion might be developed. In the conventional communications, the interference caused by the previous signaling intervals is usually called inter-symbol interference and generally compensated by the receiver using, matched filter or error correcting codes or other means. To handle the so called inter-symbol interference problem in the molecular communication, we treat this as a corrupting noise source or residual noise, n_r(t). Thus residual noise, n_r(t), accounts for interference from messenger molecules that are remained in the receiver sensing area from the last transmission. Now to investigate the statistical characterstics of this noise, we need to drive the probability density function of a messenger molecule from the previous transmission time, nT_S, in the receiver at time t. To do that, we use the fact that according to the Brownian motion process, the displacement of a molecule during an infinitesimal interval of dt seconds, can be modeled by a zero mean Gaussian distribution process with variance 2Ddt.^11,12

$X (t + d t) = X (t) + \sqrt{2 D d t} u (t)$ (18)

with D being the diffusion coefficient and X(t)=(x(t), y(t),z(t)) being the three dimensional molecular position at time t with u(t) representing a vector of multivariate normal distribution. Thus, using Eq.(12) for the displacement of a messenger molecule transmitted at time Nt_S is

$X (t) = X_{t x} + \sqrt{2 D (t - n T_{s})} u (t)$ (19)

where X_tx is the transmission location $N (O {}_{1 \times 2}, I_{2 \times 2})$ where $O_{1 \times 2}$ and $I_{2 \times 2}$ two-dimensional null and identity matrices. Hence, the probability function of being at location X(t) we have;

$P_{x}^{(n)} (x) = \frac{1}{4 π D (t - n T_{s})} \exp (\frac{- {| X - X_{t n} |}^{2}}{4 D (t - n T_{s})})$ (20)

and therefore the probability of a messenger molecule being in the sensing area Ar is

$P_{}^{(n)} = \iint_{A r} \frac{1}{4 π D (t - n T_{s})} \exp (\frac{- {| X - X_{t n} |}^{2}}{4 D (t - n T_{s})}) d x d y$ (21)

It is also true that probability distribution of K molecules from Q molecules being at the reception area is a Binomial distribution with mean QP⁽ⁿ⁾ and the variance of QP(ⁿ⁾(1-P⁽ⁿ⁾) .Since ,Q.>1 which is obvious ,then for small QP this binomial distribution can be approximated by a Gaussian distribution function of N(QP⁽ⁿ⁾ ,QP⁽ⁿ⁾ (1-P⁽ⁿ⁾) ). So, the probability density function of the process v(t)=s(t) t_bn(t) , Pv(t)= N(QP⁽ⁿ⁾ ,QP⁽ⁿ⁾ (1-P⁽ⁿ⁾) ). Hence, the probability distribution of the residual noise is as follows:

$P_{n r} (n_{r} (t)) = \sum_{n = 0}^{[\frac{t}{t_{s}}] - 1} P_{v} (v^{(n)} (t) \sim \sum_{n = 0}^{[\frac{t}{t_{s}}] - 1} N (Q p^{(n)}, Q P^{(n)} (1 - P^{(n)})$ (22)

Finally, the overall number of residual molecules has distribution of Gaussian as well, n_r ~N(α,β) where

$α = \sum_{n = 0}^{[\frac{t}{t_{s}}] - 1} Q p^{(n)} = \sum_{n = 0}^{[\frac{t}{t_{s}}] - 1} \iint_{A r} \frac{1}{4 π D (t - n T_{s})} \exp (\frac{- {| X - X_{t n} |}^{2}}{4 D (t - n T_{s})}) d x d y$

$β = \sum_{n = 0}^{[\frac{t}{t_{s}}] - 1} Q p^{(n)} (1 - p^{(n)}) = \sum_{n = 0}^{[\frac{t}{t_{s}}] - 1} (\iint_{A r} \frac{Q}{4 π D (t - n T_{s})} \exp (\frac{- {| X - X_{t n} |}^{2}}{4 D (t - n T_{s})}) d x d y) (1 - \iint_{A r} \frac{1}{4 π D (t - n T_{s})} \exp (\frac{- {| X - X_{t n} |}^{2}}{4 D (t - n T_{s})}) d x d y)$ (23)

Conclusion

In this paper, additive noise model is considered only in one scenario, that is diffusion-based. In this case, two additive noise sources are considered; as a result of thermal motions of molecules Brownian noise and, as a result of residual molecules from the previous transmission, residual noise. It is shown that the corrupted noise in the diffusion-based channel must be additive and is Gaussian with having uncorrelated and non-stationary statistics with dependence on the signal magnitude. For the future works, the investigation of the electromagnetic and electrostatic effects on the diffusion-based channel is very interesting. Finally, analysis of the channel capacity and pulse-shaping principals are very important subjects which must be addressed with great care.