This paper presents a study of plume dispersion from an electric arc-furnace, of a steel making process, in case of an accidental release due, for example, to the failure of the gas-cleaning units. The off gases released from an electric arc-furnace (EAF) are very toxic and contain Polychlorinated Dibenzo dioxins and Polychlorinated Dibenzofurans (PCDD/PCDFs), particulate matter associated with heavy metals such as lead, zinc, and cadmium among others. The study was carried out using Computational Fluid Dynamics (CFD) techniques. The mathematical model developed is three-dimensional and includes a turbulence model, namely the RNG k-ε model. The temperature of the plume is low enough to ensure safe dispersion of the particles, resulting to high concentration levels over the local area. Also, high concentration levels of toxic metals associated with the particles seem to dominate the region as well as large amount of PCDD/PCDFs. Diagrams of off gases concentration downwind of the building of the electric-arc-furnace for different temperatures are constructed and can be used to assess the consequences of the toxic release.

Keywords: dispersion, CFD modeling, Polychlorinated Dibenzodioxins/Polychlorinated Dibenzofurans (PCDD/Fs), particles

PCDD, polychlorinated dibenzo dioxins; PCDFs, polychlorinated dibenzofurans; EAF, electric arc-furnace; CFD, computational fluid dynamics; APCDs, air pollution control devices; HSE, health and safety executive; TEQ, toxic equivalent quantity

The direct smelting of iron-containing materials, such as scrap is usually performed in electric arc-furnaces (EAF), which play an important and ever-increasing role in modern steel works concepts.¹ EAF dusts are an industrial by-product. These dusts are recovered in gas cleaning units during the production of steel in electric arc-furnaces, which are fed with scrap metal. EAF dust composition can vary greatly depending on the scrap metal composition, furnace additives, operating conditions, degree of recycling of dusts in the steelmaking process and on the type of steel produced.² Dust formation is strongly linked to the process, which can be divided into five steps: furnace charging, melting, refining, slag foaming and casting.³ The PCDD/PCDFs emission concentration depends on the contaminants in the steel scrap, variations in EAF operating practices and the furnace atmosphere, the use of post combustion, EAF combustion efficiency, design and operating conditions of the gas conditioning system, and furnace off-gas temperature entering the baghouse.⁴ During the process, the fumes are extracted through an aperture in the furnace roof.⁵ These are post-combusted, cooled, and cleaned from the transported dust, which is collected in large bag filters.⁶ This dust contains hazardous, leachable elements such as zinc, lead or cadmium, which require EAF dust to be stored in specific landfills.³ Primary off-gases represent approximately 95% of total emissions from an EAF.⁷ Most of the existing plants extract the primary emissions by the 4th hole (in case of three electrodes) or by the 2nd hole (in case of one electrode).¹ Thus 85 – 90% of the total emissions during a complete cycle “tap-to-tap” can be collected.⁷ There are still very few plants which do not have a 4th hole but only a dog house.⁸ More than 50% of the EAF in the EU have, in addition to the 4th hole, a system for evacuation of the building atmosphere, especially hoods. Most of the heavy metals are mainly associated with particulate matter and are removed from the off-gas with the separated dust. The 95% of the particles are fine and have diameter less than 5 μm. This dust contains hazardous, leachable elements such as zinc, lead or cadmium.

The physical problem

In case of an accident or failure of the air pollution control devices (APCDs), the off-gases are released to the atmosphere, resulting to high concentration levels to the surrounding area and population. Computations of flow and concentration fields around buildings are a difficult task, mainly due to the presence of turbulence, buoyancy and recirculation. The dispersion pattern of the discharged plume is affected both by the plume discharge conditions, the heat release, the vertical momentum and the way the plume is distributed over the building. There is also a complicated interaction with the wind flow around the building. The flow and dispersion fields around buildings have been investigated by a lot of researchers both in the wind tunnel and by computational methods. Markatos et al.,⁹ presented a Computational Fluid Dynamic program (CFD) developed for the prediction of flow and dispersion of warehouse fire products into the nearby environment.^9–12 A similar method is applied in the present work, assuming that the particles form a pollutant that is released into the atmosphere, in the same manner as the fire products do. A lot of attention has being given to the building downwash effects. The ADMS code includes a module for building effects and comparisons with wind tunnel data¹³ showed that ADMS is able to predict dispersion during the various stages of fire development.¹⁴ An overview of the building downwash effects is given by Canepa.¹⁵ Field and wind tunnel investigations of plume dispersion around obstacles can be found in the recent work of Mavroidis et al.,¹⁶ where comparisons between field and wind tunnel results are considered.¹⁶

The methodology

The simulation of the problem considered in this paper is difficult due to the fact that there is no or few experimental data for the rate of emission, the discharge velocity and the temperature of the hot gases, and for the concentration field downwind the electric arc-furnace. Also, it is not known where the plume discharge will occur from the building structure so it is necessary to adopt a methodology for the simulation of the release. The research group of Markatos^9–12 determined the “lift-off” condition of buoyant plumes released from a warehouse on fire and, in order the results to be applicable without the necessity of other simulation models (e.g. for the rate of discharge, the gases temperature, the rate of the toxic substances), they presented an accomplished methodology of risk assessment from fires in warehouses storing toxic substances. The proposed methodology calculates the mass and heat source terms through an approach of standardization. This methodology was derived from the practices of Health and Safety Executive (HSE), which is responsible for the implementation of the European Communities’ Seveso Directive II in the United Kingdom.¹⁷ According to that methodology, the basic logic of the “worst case” analysis is adopted so that when someone takes all the conditions in their worst interpretation he would derive extreme results that will not appear in a case of a real accident. So, the worst consequences are observed at the initial stages of a fire development where the “worst case” scenario arises from one typical roof light of 3m² broken on the roof of a typical warehouse of the EC.

Assumptions

According to the “worst case” scenario the assumptions used in the simulation of the problem studied are:

a) It can be assumed that the electric arc-furnace building is similar to a typical warehouse of the EC but with a slope on the roof with dimensions of 60m x 17.5m x 30m in the x-y-z directions, respectively, and with a roof slope of 15^oC.

b) The widest face of the building is set across the flow (according to the “worst case” scenario) and at 80m distance from the origin of the computational domain.

c) When EAF operates normally, the cleaned off gases are usually driven to a stack through which they are emitted into the atmosphere. Typical parameters of stack gas emission from an EAF in Greece are shown in

Table 1 and will be used later for a comparison with the accidental release.

 The temperature of the gases that are emitted directly from the EAF is not constant and depends on the stage of the operation of scrap. The scrap is heated from room temperature to above 1600^oC, so it may be assumed that off gases directly from the EAF can have a mean temperature of 800^oC.

When the gas-cleaning unit is out of order, then the gas plume will fill the building, and will be discharged through apertures in the roof of the building at a lower temperature of about 100-400°C maximum, as 30% of the heat may be transferred to the fabric of the building.¹⁸ The discharge will take place through two openings of 3m² on the roof and at the centre of the EAF building.

Primary off gas measurements directly from the EAF are difficult to be done due to high gas temperatures and the presence of dust. Chang et al.,¹⁹ made measurements near EAF, and before the APCDs, and found a very high concentration level of particles, about 10830 mg/Nm³. For a steel industry with production of 1100tn scrap/day and for a typical gas emission rate of 125 Nm³/s (Table 1), the previous measurement of particles results to 106.3 kg/tn LS (LS: liquid steel). This value is about ten times higher than the emission factor of 10 kg/tn LS given in literature.¹ For this work, and for a steel industry with production of 1100tn scrap/day, the dust rate of the primary off gases in case of an accident is assumed to be 10 kg/tn LS, with the chemical composition shown in Table 2.¹ The discharge velocity of the gas was equal zero. The flow of gases and particles is assumed to be single phase, since 95% of the particles discharged are very fine and have diameter less than 5μm.¹

d) Almost 99% of the PCDD/Fs emission directly from the EAF exists in particulate phase, according to Chang et al.,¹⁹ Measurements at point near to the two EAF he examined indicated that the total Toxic Equivalent Quantity (TEQ) concentration, prior to APCDs was 96.8ng I-TEQ/Nm³. This measurement is taken fairly close to the EAF and at temperature of 379 ^o General PCDD/Fs emission factor is 0.07-9μg I-TEQ/tn LS compiled from various references after APCDs.¹ There are two main formation mechanisms of PCDD/PCDFs in an EAF:²⁰

I) Reaction of organic precursors, such as chlorophenols, on the surface of dust particles at temperatures over 300°C (precursors enter the process with scrap impurities like lubrication and cooling oil, paint and plastics).²¹

II) PCDD/Fs are formed from the de-novo synthesis without organic precursors, i.e. formation out of carbon, oxygen and metal chlorides (e.g. copper chloride) at temperatures between 250–500°C in the off-gas. In this case copper chloride acts as a catalyst. PCDD/Fs are highly viscous liquids at temperatures up to 300°C and can therefore be adsorbed at the surface of dust particles.

So, assuming an accidental release from an EAF, the off gases from the EAF are cooled down slowly from the mean temperature of 800^oC inside the EAF building, as the 30% of the heat is transferred to the fabric of the building resulting both I and II mechanisms of formation of PCDD/Fs to be significant. The value emission then of 96.8 ng I-TEQ/Nm³ can be used to assess the consequences of the release. EC has taken a limit of 0.1 ng I- TEQ /Nm³ emission for PCDD/Fs from waste incinerators to the atmosphere.

The physical problem described above is simulated using computational fluid dynamics (CFD) techniques.

Governing equations

The mathematical model used in the present work consists of the full partial differential equations that describe turbulent flow and heat and mass transport. For the simulation of turbulence, use is made of the so- called RNG k-ε model of turbulence,²² a model that appeared promising from extensive other work in the environmental field by the last two authors. For the present work the RNG k-ε model was modified to account properly for the effect of buoyancy forces in the production/destruction of the kinetic energy of turbulence. The mathematical model involves the continuity equation, the three momentum equations and equations of conservation of the scalar variables h (enthalpy), k (turbulence kinematic energy), ε (eddy dissipation rate), and C (chemical species concentration).²³

Continuity equation: $\frac{\partial Ui}{\partial xi}=0$ (1)

Momentum equations:

  $Uj\frac{\partial Ui}{\partial xj}=-\frac{1}{\rho }\frac{\partial P}{\partial xi}+\frac{\partial }{\partial xj}\left[v_{eff}\left(\frac{\partial Ui}{\partial xj}+\frac{\partial Uj}{\partial xi}\right)\right]+gi\beta \Theta$ (2)

where  , the effective kinematic viscosity,  kinematic viscosity , turbulence kinematic viscosity

Energy equation : $Uj\frac{\partial h}{\partial xj}=\frac{\partial }{\partial xj}\left\{\left(\frac{v}{{\mathrm{P}}_r}+\frac{v_t}{\sigma T}\right)\frac{\partial h}{\partial x_j}\right\}$ (3)

Concentration equation: $Uj\frac{\partial C}{\partial xj}=\frac{\partial }{\partial xj}\left\{\left(v+\frac{v_t}{\sigma C}\right)\frac{\partial C}{\partial x_j}\right\}$ (4)

Equation for kinetic energy of turbulence:

$Uj\frac{\partial k}{\partial xj}=\frac{\partial }{\partial xj}\left\{\left(v+\frac{v_t}{\sigma k}\right)\frac{\partial k}{\partial x_j}\right\}+P_k+G_b-\epsilon$ (5)

Εquation for dissipation rate of turbulence:

$Uj\frac{\partial \epsilon }{\partial xj}=\frac{\partial }{\partial xj}\left\{\left(v+\frac{v_t}{\sigma \epsilon }\right)\frac{\partial \epsilon }{\partial x_j}\right\}+\left(c_{\epsilon 1}{P}_k-c_{\epsilon 2\epsilon }+c_{\epsilon 3}{G}_b\right)\frac{\epsilon }{k}-\frac{c\mu {\eta }^3\left(1-\eta /{\eta }_0\right)}{1+{\beta }_1{\eta }^3}$ (6)

where:$v_t=c_{\mu }\frac{k^2}{\epsilon }=c_{\mu }{k}^{1/2}{L}_k$ ,$P_k=vt\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\frac{\partial U_i}{\partial x_j}$ , the rate of production of turbulence energy

, the term of production/destruction of turbulence energy due to the action of buoyancy forces.^23,24

$\beta =\frac{1}{p}\frac{\partial p}{\partial T}=\frac{1}{Tref}$, $\Theta ={\rm T}-{{\rm T}}_{ref}$,$\eta =\frac{Sk}{\epsilon }$,$S={\left(S_{ij}{S}_{ij}\right)}^{1/2}$

, Θ=Τ-Τ_ref,,

where $S_{ij}\frac{1}{2}\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)$ the mean rate of strain and U the velocity of the mean flow.

 The values of the constants appearing in the equations above are given in Table 3.

Geometry and grid development

For the application considered the computational domain is three-dimensional with dimensions of 718mx300mx232m (x-y-z) and, because of symmetry, use is made of half of it in the z direction, to save computational time. The computations were carried out by using a non-uniform cartesian grid, which was coarse near the outflow and inflow boundaries of the computational domain and fine enough near the building and the sources.²⁵ Many runs were performed to ensure grid independency of the results. The grid finally used was consisting of 372592 cells, 44x73x116 (N_xxN_yxN_z) (Figures 1&2), and the results obtained by that grid appeared virtually independent of further refinement (up to roughly 900000 cells).

Figure 1 The grid in the y-z plane.

Figure 2 The grid in the x-y plane.

Boundary conditions

The inlet velocity is approximated by a 1/7-th power law (at the height of 8m velocity has the value of 5m/s) and the turbulence kinetic energy k is taken from experimental data.²⁶ The inlet turbulence dissipation rate, ε, is computed as follows:

where: is the mixing length, is the Von Karman constant (=0.415), is the distance from the ground,  is the boundary layer thickness (=300m). At the outlet, the flow is taken as parabolic and at the top boundary the normal change of the variables is set to zero. The pressure is taken as uniform outside the flow field. At the solid boundaries of the computational domain, the so-called “Wall Functions” are used.²⁴ The atmosphere is assumed adiabatic.

 Computational details

The general purpose CFD code PHOENICS^28,29 along with the solution procedure called SIMPLEST²³ was used for the computational analysis. The simulation runs were performed on a Pentium 4/2.8GHz and convergence was achieved by applying false-time-step under-relaxation techniques. The number of the iteration sweeps of the computational domain required for full convergence was 3000-4000 and each sweep required 15-20s CPU time.

A parametric study was performed for five different temperatures, 0°C , 100°C, 200°C, 300°C and 400°C. The ground concentration downwind of the building is shown in Figure 3.

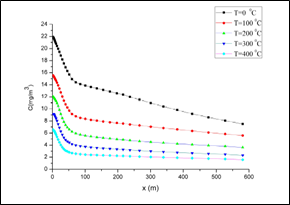
Figure 3 Ground concentration downwind of the building for different temperatures of the discharged plume.

The plume height downwind of the electric arc-furnace can be seen in Figure 4

Figure 4 Plume heights for different temperatures vs downwind distance from the electric arc-furnace.

 Figure 5 presents the flow field around the electric arc-furnace, for different temperatures and Figure 6 the contours of enthalpy for each case studied.

Figure 5 Flow field for different temperatures.

Figure 6 Enthalpy contours for different temperatures.

The flow field around the building is complex. The present aerodynamics interactions with the buoyant plume results in a very complex flow field with recirculating zones upwind, upon and downwind of the building (Figures 5&6). As the temperature of the off gases rises, the interaction between the two plumes is bigger having as a result lower concentrations downwind of the building at the ground level. For the no buoyant case (T=0°C) the ground level concentration is at maximum and it is more than 10 mg/m³ at 200m downwind of the electric arc-furnace, while the plume touches the ground over 300m . As the temperature increases, the plume height increases and the ground concentrations decrease resulting to safer dispersion of the plume. For the maximum temperature studied (T=400°C) it can be seen that the concentration is over 4.5 mg/m³ for the first 200m downwind the source and it doesn’t fall below 1.5 mg/m³ for all the field studied.

Therefore, from the results obtained, it can be concluded that in case of an accident in an electric arc-furnace, the concentration of the toxic fine particles will be high enough in the near field. The particulate concentration in the near region of 600 m of the EAF, it seems to be very high resulting to a mean value of 5-10 mg/m³. Also, for the same region around the EAF, toxic metals such as As, Pb, Cd will dominate with mean concentrations of about 2, 150, 15 μg/m³ respectively. The resulting elemental concentrations for different temperatures from the composition of the off gases according to Table 2 are shown in the Appendix for 50, 200 and 500m distances downwind the EAF. If it were taken into account the value of 10830 mg/Nm³ concentration of particulate matter found by Chang et al.,¹⁹ in the EAF, then the concentration of particles and toxic metals given above would be 10 times higher.

The above hazard can be easily be clear comparing these values with the result obtained assuming a safe off gas dispersion through the stack of the EAF normally working. A gaussian model was used assuming D stability class with wind velocity 5m/s at stack height. The particle concentration is shown in Figure 7. It is clear that particle concentration has a peak of 5μg/m³ at about 1600 m from the stack, ensuring safe dispersion of the plume of the off gases in the atmosphere. The mean particle concentration value of 5-10 mg/m³ is 1000-2000 times higher than the Gaussian peak value. The Chang et al.,¹⁹ measurement could give 10000-20000 times higher than the Gaussian peak value resulting to very high concentrations in the near region of the EAF.

Figure 7 Particles dispersion from a typical stack of EAF in Greece.

The PCDD/Fs exhibit a hydrophobic nature and resistance towards metabolism. Hence, these chemicals persist in the environment and bioaccumulate in fatty tissues of animals and humans.²⁷ Assuming that the stack emits the limit of 0.1 ng I-TEQ/Nm³ PCDD/Fs then it is obvious that the Chang et al.,¹⁹ measurement value of 96.8 ng I-TEQ/Nm³ taken as PCDD/Fs accidental release in the off gases, is about 1000 times higher. In order to be clear, the emission level of PCDD/Fs in case of an accident, it can be said that about a nine hour accident on the APCDs and release of the toxic plume of off gases in the atmosphere without any cleaning operation, will have the same toxic consequences of the PCDD/Fs emission level of a year, when it is released in the atmosphere with the limit of 0.1 ng I-TEQ/Nm³ from the stack.

In this paper the consequences from an accidental release from an electric arc-furnace have been studied using CFD techniques with a proper methodology. The release consists of toxic particles which 95% are very fine (diameter < 5μm). The study involved also a parametric study for 5 different temperatures (0°C–400°C) of the release from two openings on the roof. It is concluded that in the neighborhood of the electric arc-furnace (of about 1 Km), the ground concentration of the toxic fine particles is very high and it doesn’t fall below 1 mg/m³. Also, the concentration of toxic metals, such as As, Cd, Pb, associated with the particles is very high. The PCDD/Fs emission to the atmosphere assuming a 9-hour accident to the APCDs resulted to a high concentration as high as a year emission through a clean gas process with a limit on emission of 0.1ng/Nm³. So, in a case of an accident or no working of the gas cleaning system of an EAF the environment can become very pollutant, around a 1Km distance around the EAF building, with a toxic plume of particulate matter with toxic metal, such as lead, zinc and cadmium among others, as well as with PCDD/Fs.

None.

The author declares there are no conflicts of interest.

1. European Commission, Integrated Pollution Prevention and Control (IPPC) Best Available Techniques Reference Document on the Production of Iron and Steel, December 2001
2. R Mecozzi, L Di Palma, D Pilone, et al. Use of EAF dust as heterogeneous catalyst in Fenton oxidation of PCP contaminated wastewaters. Journal of Hazardous Materials. 2006;137(2):886–892.
3. Anne Gwénaëlle Guézennec, Jean Christophe Huber, Fabrice Patisson, et al. Dust formation in Electric Arc-furnace: Birth of the particles. Powder Technology. 2005;157(1–3):2–11.
4. Sofilić T,  Jendricko J, Kovacević Z, et al. Measurement of polychlorinated dibenzo-p-dioxin and dibenzofuran emission from EAF steel making process. Archives of Metallurgy and Materials. 2012;57(3):811–821.
5. Collection System contains oily furnace fumes, Filtration and Separation. 1999;36(5):9.
6. Friedrich Loffler, Hans Dietrich, Werner Flatt. Dust Collection with bag filters and envelope filters. 1988.
7. European Commission. Technical Note on the Best Available Technologies to Reduce Emissions of Pollutants into the Air from Electric Arc Steel Production Plants. 1994.
8. Roederer C Gourtsoyannis L. Coordinated Study 'Steel-Environment. DG XII - EUR 16955 EN. 1996.
9. CΕC. Step Programe Major Hazards Arising from Fires in Warehouses and Chemical Stores. MIH Project. 1996.
10. Christolis MN, Christidou CA, Boudouvis AG, et al. Modelling Pollutants Dispersion around Buildings on Fire. Transactions on Ecology and the Environment. 1995;6:85–92.
11. Christolis MN, Christidou CA, Boudouvis AG, et al. Flow and pollution fields around buildings in fire. Seminar on Industrial Fires, European Commission, Cadarach, France. 1994.
12. Sideris GM, Christolis MN, Markatos NC. Numerical Simulation of Pollutants Dispersion around Warehouse on Fire. Scientific Computing to Computational Engineering. 2004.
13. Hall DJ, Kukadia V, Walker S. et al. Plume dispersion from chemical warehouse fires. Building Research Establishment, Client Report CR 56/95 prepared for the European Commission on STEP project no CT 90-0096, for the Toxic Substances Division, Department of Environment. 1995.
14. Carruthers DJ, Mckeown AM, Hall DJ, et al. Validation of ADMS against wind tunnel data of dispersion from chemical warehouse fires. Atmos Environ. 1999;33(12):1937–1953.
15. Canepa E. An overview about the study of downwash effects on dispersion of airborne pollutants. Environmental Modelling & Software. 2004;19(12):1077–1087.
16. Mavroidis I, Griffiths FR, Hall DJ. Field and wind tunnel investigations of plume dispersion around single surface obstacles. Atmospheric Environment. 2003;37:2903–2918.
17. Loai Aljerf, Nuha Al Masri. Persistence and Bioaccumulation of persistent organic pollutants(POPs) in the soil and aquatic ecosystems: Syrian frontiers in ecology and environment. Sustainability in Environment. 2018;3(4):358–386.
18. HSE. Assessment of Safety Reports for Chemical Warehouses. 1997
19. HSE. Safety report assessment guide: Chemical warehouses—hazards & criteria, Health and Safety Executive. 2002.
20. Chang MB, Huang HC, Tsai SS et al. Evaluation of the emission characteristics of PCDD/Fs from electric arc-furnaces. Chemosphere. 2006;62(11):1761–1773.
21. Report: Opportunities for reduction of dioxin emissions from the metallurgical sector in Poland. 2005.
22. Yakhot V, Smith LM. The Renormalization group, the epsilon expansion and derivation of turbulence models. Journal of Scientific Computing. 1992;7:35–61.
23. Markatos NC, Malin MR, Cox G. Mathematical modelling of buoyancy-induced smoke flow in enclosures. Int J Heat Mass Transfer. 1982;25(1):63–75.
24. Suhas V Patankar. Numerical Heat Transfer and Fluid Flow. Mc Graw-Hill, 1980.
25. Launder BE, Spalding DB. Mathematical models of turbulence. Academic Press. 1972.
26. Huber, Alan H. The influence of building width and orientation on plume dispersion in the wake of a building. Atmospheric Environment. 1989;23(10):2109–2116.
27. US. EPA, Exposure and Human Health Reassessment of 2,3,7,8-Tetrachlorodibenzo-p-Dioxin (TCDD) and Related Compounds National Academy Sciences Review Draft, 2000.
28. www.cham.co.uk
29. Karadimou DP, Markatos NC. Study of the numerical Diffusion in Computational Calculations’, in book ‘Numerical Simulations in Engineering and Science. 2018.