Recurrent extreme weather patterns under global warming impose an urgent need to recognise and conserve species likely to be impacted. In temperate areas, evidence is growing for species shifting ranges along temperature gradients. Comparable conjecture is gaining traction around changes in herbivores distributions in African savanna. Nonetheless, this needs careful investigations particularly because savanna antelopes establish range consequent of forage availability driven by rainfall. Rainfall events are widely disparate thus, range shifting along clear-cut gradients maybe uncertain. We investigated tsessebe, roan and sable antelope distributions in the 200 00km² -Kruger National Park because these species exhibit a few traits typically used to predict climate change vulnerability. We predicted that extirpations would occur from regions that become marginal in terms of forage production, but persisting where conditions remain more suitable. We evaluated associations between range occupations for these species relative to rainfall, temperature, and forage availability for a period extending over two decades examining if distribution changes followed particular gradients.

Results showed extirpations from areas that had become less suitable, but persistence where conditions remained favourable with respect to forage availability. Number of herds rather than herd-sizes generated the range changes. During high rainfall years, the 1970s, numerous herds had established and ranges expanded, stabilizing early 1980s, and thereafter ranges progressively contracted following prolonged moisture deficit periods, after 1987. Remnant and small herds persisted on discrete on patches that retained adequate forage in formerly contiguous ranges. Thus, in heterogeneous savanna, assumptions on range shifting along climatic gradients may not hold.

Keywords: species distributions, climate change, edge of range, habitat heterogeneity, range contraction, rainfall influences

Studies have shown direct correlations of weather particularly extreme conditions with organisms’ reproductive success through effects such as rainfall, droughts, and heatwaves,^1,2 or indirectly via food availability.³ For many species, weather conditions impose natural limits to distributions.^4‒11 Growing evidence suggest that climate change modifies the weather impacts on species threatening their existence.^12‒16 Evidence abound for local extinctions consequent of shifting distributions at the warm edges of species’ ranges. This cold-edge expansion and warm-edge contraction documented for several plant and animal taxa is one of the most studied signals of biotic change from a warming climate.^14‒17 However, such responses are relatively well characterised for temperate latitudes, but less well understood in savannas.

Whilst the range shifts poleward and towards higher elevations in temperate latitudes highlight environmental gradients, principally, a warming temperature, as influential,^4,14‒16,18 the same temperature factor might not hold for antelopes in savanna. Whist high ambient temperatures or heat stress may constrain dissipation of body heat and subsequently reduce foraging time,¹² rainfall ultimately drives range establishment.^3,19‒22 Even though limited physiological tolerances to high temperatures seemingly could be a factor that causes climate change to threaten their persistence, antelopes in drier regions display heat-avoidance behaviours reducing the negative impacts. Herbivores rest during midday and forage at dusk, dawn, or during night-time.²³

A key ecological consideration is that savanna systems are hugely heterogeneous concerning forage productivity²⁴ consequent of the widely disparate moisture availability. Rainfall is discrete, intermittent, and with much variability in space and between seasons leading to local variations in habitat suitability.^25,26 Although no change in mean is expected, rainfall variability is predicted to increase for South Africa under climate change.²⁷ A warming savanna would mainly make rainfall less effective. The above raises a key question, particularly for large antelopes, around the universality of the assumption that range shifts will occur along environmental gradients. No studies, to our knowledge, has tested these pervasive assumptions for savanna antelopes. Furthermore, assessments of climate change vulnerability often use limited data to identify species lacking traits assumed to confer an ability to persist under changing environmental conditions. However, those assessments have characterised the most vulnerable species as having restricted geographical ranges, specialised resource requirements, narrow physiological tolerance, slow reproductive rates, and poor dispersal abilities. The sable antelope (Hippotragus niger), roan antelope (Hippotragus equinus) and tsessebe (Damaliscus lunatus) it the Kruger National Park (KNP) in this description. Thus, the KNP is an ideal environment to test such predictions. It is located at the edge of the geographic range of the three antelope species in Africa. Long-term datasets of their distributions, rainfall as well as temperature records (1963-2005) are available.²⁸ Populations of these species have contracted to 25% or less of their peak abundances following prolonged moisture deficit periods, 1982-1995.^29,30 Because the three species occur as discrete herd units,^31,32 ranges they occupied over time can be established. Effects of competitors and natural enemies on these species have been documented elsewhere.^33‒36

Climate change imposes an urgent need to recognise and direct conservation efforts towards to species likely to be worst affected. Knowledge of how savanna ungulates respond to a changing climate is critical for determining appropriate conservation methods. Here, distributional changes for tsessebe, roan and sable antelopes were investigated to establish if responses of these antelopes to a changing climate were qualitatively similar to well-studied groups elsewhere. The prediction was that extirpations would occur from regions that become marginal with respect to forage production, but persistence where conditions remain suitable.

Study area and species

The Kruger National Park covers almost 20,000km² of the eastern Lowveld region of South Africa (Figure 1). Precipitation occurs mainly between October and March. Annual rainfall totals decline from around 750mm in south-west to 450mm in north-east.³⁷ In north-west KNP, rainfall totals rise locally to 600mm. Granite-derived sandy soils prevail in the west and basaltic clays to the east of KNP. In the southern half of the park, vegetation is predominantly knob thorn (Acacia nigrescens) - marula (Sclerocarya birrea) on basalt, and bush willow (Combretum spp.) - silver cluster-leaf (Terminalia sericea) savanna on granite. In the northern half, mopane (Colophospermum mopane) savanna woodland or shrubland predominates on both substrates; tree savanna on granite but shrub savanna on basalt.

Figure 1 Study area: Kruger National Park, South Africa.

Tsessebe, roan and sable antelopes typically occur as spatially discrete herds units numbering from 2-31 animals consisting of mostly females and young,³⁸ frequently accompanied by a local territorial male. Herd home ranges cover 3-15 km².^39,40 

Data collection

Geology

KNP research services provided data on 15 geological zones.⁴¹ Seven geological substrates were used in this analysis after Chirima.²⁶ Some geological zones were amalgamated by grouping those yielding similar soil characteristics and water retention capabilities. The seven were basalt, gabbro, karoo sandstones plus shales, granite, rhyolite, sandstone and aeolian sand, in descending order of soil fertility.

Rainfall

A dataset from the Agricultural Research Council of South Africa (ARC) weather station network, additional records from the South African Weather Service and KNP weather stations (with a recording period of 10 years or more) were applied as the measure of rainfall. A rainfall surface (map) for KNP was created applying regression techniques in Arc Map 10.3 (Esri, Redlands, CA, USA). The rainfall surface was used to calculate annual mean rainfall on a 1km resolution. A long-term mean rainfall figure for each calendar month was extracted per weather station. A trend surface was created from this monthly data using inverse distance weight interpolation method. A spatial filter was applied to the interpolated surface to create a smooth trend surface. Regression analysis was applied to relate the difference between the rainfall value at a specific station and the value given by the trend surface to topographic indices like terrain ruggedness, rain shadow, aspect, etc. The relationship and trend surface for each month was used to model a mean rainfall surface from spatial topographic indices in Arc Map 10.3 (Esri, Redlands, CA, USA). To obtain an annual total mean rainfall surface, the individual monthly surfaces were summed. Mean annual rainfall values were extracted for all the stations and used to create the mean monthly rainfall surfaces.

Vegetation index

The Normalized Difference Vegetation Index (NDVI) for selected periods was retrieved from the Advanced Very High Resolution Radiometer (AVHRR) sensors on board the NOAA satellite series. The NDVI data were downloaded, georeferenced, and missing data pixels removed. The annual maximum, minimum and mean statistics were calculated for selected periods: 1977-81, 1982-86, 1987-91, and post-1991-2005.

Temperature

A temperature surface (map) was created from 1920-1999 data downloaded from the ARC databank in Arc Map 10.3 using regression analysis and spatial modelling techniques. The mean annual temperature surface and the maximum temperatures extracted for each grid cell are indicative of possible heat stress. Regression analysis was used to relate the maximum temperature per month averaged over the year to topographic indices such as altitude, aspect and slope. The following additional variables were derived: the long-term minimum temperatures for July and the long-term maximum temperatures for January.

Animal counts

A pilot, four observers and a recorder collected geographical locations of antelope herd units, herd sizes as well as number of calves during annual aerial surveys from May to August using a fixed-wing aircraft in transects 800m apart.²⁸ Locations records amalgamated over 5-year periods provided a reliable record of the presence of antelope herds. Assuming a sighting probability of around 0.7 for medium size antelopes such as those considered here;⁴² the chance of missing an existing herd during surveys over 5 consecutive years is 0.24%.

Data analysis

Assessment of range shifts

Range occupation patterns were modelled, mapped, and distribution changes per species assessed for periods 1977-81, 1982-86, 1987-91, and post-1991-2005, applying the Adaptive Local Convex Hull (a-LoCoH) method^43,44 in Arc Map 10.3 (Esri, Redlands, CA, USA). The method is highly accurate at identifying non-occurrence gaps within a range.^44,45 The Adaptive Local Convex Hull applied the minimum spurious hole covering (MSHC) values of a and k derived following a procedure outlined in Getz et al.⁴² and Chirima & Owen-Smith.⁴⁴ Initially, the value of k (minimum neighbouring points required to construct a polygon) was fixed at 3, and the value of a (including all points within a radius such that the distances of these points to a reference point sum to a value <a) was fixed at 1 m following Chirima & Owen-Smith.⁴⁴ A curve of the area of the estimated distribution range was then plotted versus increasing values of a and k (one at a time) to find a plateau (i.e. the minimum MSHC value). Thereafter, the joint MSCH values of for a and k were used to model and map range occupation per period. Following Chirima & Owen-Smith,⁴⁴ the 95% isopleths represented total distribution and the 75% isopleths distinguished core from marginal regions.

Statistical procedures

In order to discriminate the influences of rainfall or temperature on range shifts, the first step was to account for basic influences of geology on antelope distributions. Geology designates regions that allow a species to persist (i.e. spatial extent of fundamental niche).^46,47 The next step was to investigate the influence of climate factors on range expansions or contractions in occupied geologies.

Model fitting

A KNP 5 x 5 km tile shape file was used as the basis for all analyses, following Chirima & Owen-Smith.⁴⁴ Tiles covering less than a third (8.3km²) of the species’ home range area extents and occurring along park boundary fences were excluded. Range was considered occupied if a herd was recorded on at least on two occasions from 1977-2005 in that same tile. The latter minimized chances of including herd locations recorded outside usual range. A herd was defined as two or more individuals, including males and breeding herds, seen at any one particular location at the same time. Tiles containing multiple records of herds over the same period (1977-2005) were treated as a single “presence”.

Assessment of range expansions or contractions

The first task was checking if range occupation by a species had changed over the periods 1977-81, 1982-86, 1987-91 and for post-1991-2005. Because a herd’s occupation records for one specific period were correlated with records of the preceding period, a McNemar Test was applied in SPSS version 21 for these assessments.^48,49 Range occupation was coded 1 if present, and 0 if absent per period. The significance of the range shift was judged using Pearson Chi-square Test.⁵⁰

Assessing influences of climatic factors on range shifts

To investigate whether climatic influences were associated with the noted range contractions or expansions, a Generalized Linear Model (GLM) with a binomial link function was fitted in R software⁵¹ (R version 3.1.0 (2014-04-10) -- "Spring Dance" Copyright (C) 2014 The R Foundation for Statistical Computing). The models evaluated range changes in association with long-term rainfall, long-term NDVI, long-term minimum temperatures in the month of July, and long-term maximum temperatures in the month of January. For the variable rainfall, models were developed with records of the preceding year under analysis, because during surveys, herds were recorded up to June each year. June is a period before the rainy season for that particular year. First, effects of single terms were investigated in order to determine, which factors were closely associated with the range contractions/expansions. Dependent variables such as NDVI and rainfall as well as maximum and minimum temperatures were not included in the same model to avoid over fitting.

Step-down procedures in R software and the Akaike Information Criterion (AIC) were applied to assess the relative fit of models.^50,52 The residual deviance statistic was applied to evaluate the contribution of each predictor in the model.⁵¹ AIC model selection procedures provided the relative support for each individual model via comparing AIC values and delta Akaike (AIC Δ_i) amongst the various models.⁵² Models with delta AIC values < 2 had equally good fit and in the event of several models presenting delta AIC values of < 2, the model with the fewest parameters (i.e. the most parsimonious) was the best. Models with substantial support considered candidates for best model had within 4-7 AIC units of the best model.⁵²

Range changes

During the high rainfall years, 1977-82, sable antelope expanded range in KNP from a mean proportion of occupied tiles of 0.48 (48%) to 0.56 (56%), P=0.000) (Figure 2A). However, during the dry periods, 1982-86 leading up to 1987-91, the range contracted from 0.56 (56%) to 0.52 (52%) (P=0.034) (Figure 2A). With the prolonging of that moisture deficit period, 1991 leading to post-1992, range contracted further from 0.52 (52%) to 0.43 (43%) (P=0.000) (Figure 2A). After 1992, sable range in the park was lower than levels seen during the 1970s.

In an analogous case, tsessebe range expanded during 1977-81 from an annual proportion of 0.25 (25 %) to 0.28 (28%) P=0.012) of occupied tiles (Figure 2B). Between the periods 1982-86 and 1987-91, tsessebe range showed no changes in KNP. After the prolonged moisture deficit period, 1987 leading to post-1992, the range contracted to all-time lows from 0.29 (29%) to 0.18 (18%) (P=0.000) (Figure 2B).

Roan antelope exhibited comparable trends: range expanded from 0.17 (17 %) to 0.23 (23%) P=0.000) during the high rainfall era, 1977 to 1982 (Figure 2C). Between 1982-86 and 1987-91 the trend reversed; all previously gained range was lost with the range contracting from 0.23 (23%) %) to 0.17 (17%) (P=0.000) (Figure 2C). After 1991, there were insufficient roan herds left in KNP to run any rigorous statistical models.

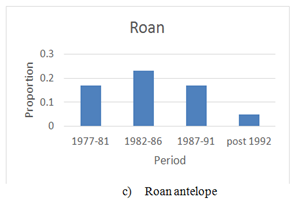
Figure 2 Changes in the proportion of tiles/areas occupied by rare antelope herds in Kruger National Park within the periods 1977-81, 1982-86, 1987-91 and 1992-97 for a) sable antelope, b) tsessebe and c) roan antelope.

Were climatic factors associated to range shifts?

Sable antelope

The association of geology with tsessebe, sable and roan antelope range occupation did not follow patterns expected regarding soil fertility. Their ranges occurred on nutrient poor granitic and sandstone substrates rather than on the rich basalt or gabbro, suggesting other factors at play. Increasing plant productivity (NDVI) was more consistent on range prevalence than increasing rainfall as a model predictor (Table 1). It appears the influence of NDVI was partly confounded with geology. Specifically, during dry seasons, granitic regions tended to be greener than areas underlain by basalt due to soil properties. This could be that increasing temperatures reduce the effectiveness of rainfall on clayey basalts and gabbro. For the three antelope species, single effects of temperature (minimum temperature in July, average annual temperature, and maximum temperature in January) did not receive enough statistical support concerning range changes.

After accounting for effects of geology, the best fitting model explaining the sable antelope range expansion phase, 1977-81, incorporated effects of forage production/or retention of green foliage as represented by long-term mean NDVI (Table 1). A model with combined additive effects of long-term mean of maximum NDVI and long-term mean annual temperature followed closely. Candidates for top model incorporated additive effects of long-term mean NDVI combined either with effects of long-term maximum temperature for January, long-term mean annual temperature, or with additive effects of long-term average minimum temperature for July (Table 1).

During the period of no range change, the best fitting model of sable antelope occurrence was additive effects of long-term average rainfall combined with effects of long-term average minimum temperature for July (Table 2). A further three models were candidates for top model. These included models incorporating main effects of long-term average rainfall, followed by a model with additive effects of long-term average rainfall and long-term maximum temperature for January, or a model with additive effects of long-term annual average rainfall plus effects of minimum temperature for July or those of long-term annual temperature.

During the period of severe range contractions, post-1992, five models were candidates for top model (Table 3 ); additive effects of long-term average of maximum NDVI either with effects of minimum temperature for July, effects of long-term annual temperature and those of long-term average temperature for January.

Tsessebe

Remarkably, the trends for tsessebe were comparable with those of sable antelope: during the period 1977-81, range expanded. Again, the top fitting models incorporated single effects of the long-term mean of maximum NDVI, followed by combined additive effects of long-term average maximum NDVI with those of long-term average annual temperature, then additive effects of long-term average maximum NDVI combined with effects of long-term average maximum temperature in January. The next candidate models incorporated additive effects of long-term average maximum NDVI with long-term average minimum temperature for July (Table 4).

During the period of no range change, 1982-86, the four best fitting models of occurrence of tsessebe range are presented in Table 5A. The top model incorporated combined additive effects of long-term average rainfall and those of long-term average maximum temperature for January, followed by a model incorporating combined additive effects of long-term average rainfall and effects of long-term annual average temperature. The next candidate models incorporated single effects of long-term average rainfall, followed by a model incorporating combined effects of long-term average rainfall combined with additive effects of long-term average minimum temperature for July (Table 5A).

During the range contraction period, 1987-91, the best fitting models explaining tsessebe range remained the same as the previous period. The key effects were those of long-term average rainfall, additive effects of long-term average rainfall with the following: effects from long-term average maximum temperature for January, with additive effects of long-term average annual temperature as well as with effects of long-term average minimum temperature for July (Table 5B). A model with single effects of long-term mean NDVI exhibited adequate fit. [All the above models had values of AIC weights of less than 0.02.].

During the period of severe range contractions, post-1992, the best fitting model of tsessebe range occupation incorporated single effects of long-term average rainfall. The next best fitting models included additive effects of long-term average rainfall with effects of long-term average minimum temperature for July. The next top candidate models incorporated additive effects of long-term average rainfall with effects of long-term average annual temperature and with long-term average maximum temperature for January respectively (Table 6).

Roan antelope

Comparable to the other two antelopes, roan range expanded during the wet 1977-81 period. The best fitting model for that occupation incorporated additive effects of long-term average maximum NDVI with long-term average annual temperature, followed by additive effects of long-term average maximum NDVI with those of long-term average maximum temperature for January. The next best fitting model incorporated additive effects of long-term average maximum NDVI and effects of long-term average annual temperature, then single effects of long-term average maximum NDVI and long-term mean NDVI average respectively (Table 7).

During the period of no range change, 1982-86, the best fitting model of occurrence incorporated additive effects of long-term average rainfall and effects of long-term average maximum temperature for January (Table 8). The next best fitting model incorporated additive effects of main effects of long-term average rainfall combined with effects of average annual temperature. These were followed by a model incorporating combined additive effects of long-term average rainfall with long-term average annual temperature, then a model with single effects of long-term average rainfall and additive effects of main effects of long-term average rainfall combined with effects of average minimum temperature in July.

During the period of severe range contractions, post-1987, the best fitting model of roan antelope range prevalence was the single effects of long-term average rainfall. This was followed by additive effects of average rainfall with effects from long-term average maximum temperature for January, long-term average annual temperature and with long-term average minimum temperature for July with AIC weights of 0.21, 0.19, 0.16 respectively, indicating a good fit (Table 9).

Distribution pattern shifts

Sable antelope showed a patchy distribution spread throughout KNP, but with a concentration towards the west (Figure 3). Their distribution expanded into the northern half of KNP between 1977 and 1986, associated with the high rainfall period. The increase in number of herds between 1977 and 1986 (Figure 4A) was coupled to a substantial increase in occupied range. Following the decline of herd units after 1987, their range contracted disparately mostly in the western and southern regions of the northern half of KNP, and in the eastern margins of the south-western region. The range contractions accentuated post-1990. A sable antelope range decrease following a specific gradient was not evident. These observed patterns were replicated in the case of tsessebe and roan antelope.

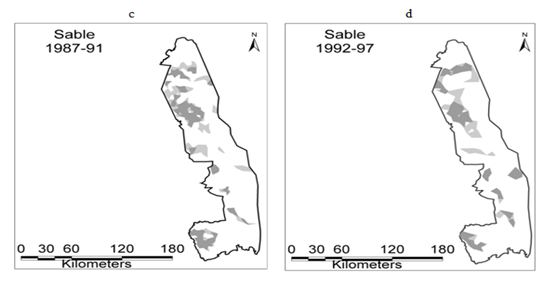
Figure 3 Changes in distribution of sable antelope herds in Kruger National Park mapped by Local Convex Hull method within four periods: (a) 1977-81, (b) 1982-86, (c) 1987-91, (d) 1992-97. Overall ranges are bounded by 95% isopleths, while darker grey regions represent concentration areas within 75% isopleths.

Tsessebe initially occurred continuously throughout the eastern region of the northern half of KNP, while an isolated subpopulation occupied the south-eastern region of central KNP (Figure 5). No range change took place until after 1991, when the northern range shrunk as well as the disappearance of the south-western range. As was the case with sable, the number of tsessebe herds increased between 1977 and 1991, after which herd counts exhibited a downward trend (Figure 4B).

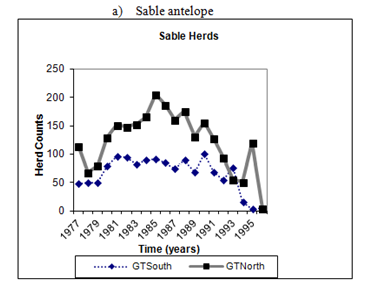
Figure 4 Changes in herd counts in the southern half (GT South) and northern half (GT North) of Kruger National Park from 1977-97 for a) sable antelope, b) tsessebe and c) roan antelope.

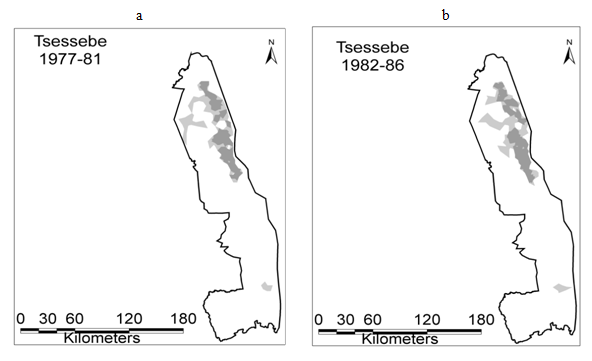
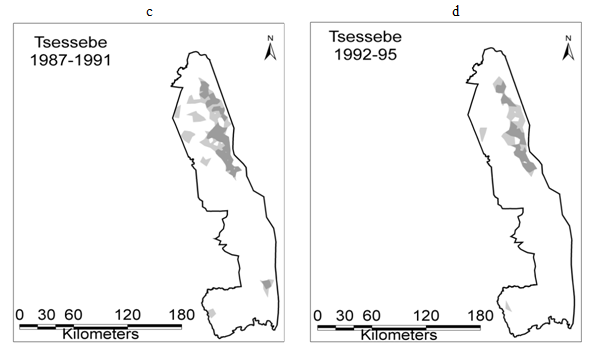
Figure 5 Changes in distribution of tsessebe herds in Kruger National Park mapped by Local Convex Hull method within four periods: (a) 1977-81, (b) 1982-86, (c) 1987-91, (d) 1992-97. Overall ranges are bounded by 95% isopleths, while darker grey regions represent concentration areas within 75% isopleths.

Prior to 1982, roan antelope occurred on two distinct ranges in the north-east and far north (Figure 6). Three isolated herds existed in the western region of the northern half of the park, plus a remotely situated herd in the south. Range shrinkage was evident after 1987. Specifically, the isolated herd in the south and the other one in the south-western region of the north had disappeared by 1989, followed by all remaining herds in the north, including one large subpopulation by 1996. The four herds that remained in the far north in 1992 had decreased to just two herds by 1996 (Figure 4C) (representing the entire free-ranging population of roan antelope left in the park).

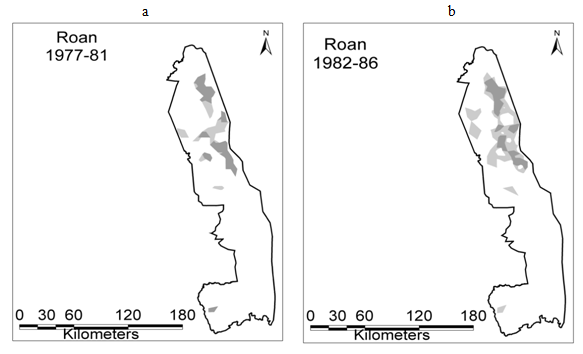
Figure 6 Changes in distribution of roan antelope herds in Kruger National Park mapped by Local Convex Hull method within four periods: (a) 1977-81, (b) 1982-86, (c) 1987-91, (d) 1992-97. Overall ranges are bounded by 95% isopleths, while darker grey regions represent concentration areas within 75% isopleths.

The study was aimed at assessing whether changes in weather components associated with global warming elicited distribution responses in tsessebe, sable and roan antelopes (in savannas) in a comparable manner to taxa elsewhere. Contrary to common assumptions, antelope range changes did not follow clear-cut rainfall or temperature gradients in Kruger National Park. The three species persisted on some patches in the drier regions of the park and disappeared from the wetter southern sections of the park following periods of persistent moisture deficit. For all three species, the number of herds rather than sizes of herds generated the observed range occupation changes. It appears that the effectiveness of moisture on forage production was the key driver to changes in herd numbers. Herd numbers increased and subsequently ranges expanded during high rainfall periods through the 1970s, then progressive receding of ranges after a period of persistent moisture deficit. NDVI rather than rainfall showed a statistically stronger relationship to observed changes suggesting it more accurately reveals the effectiveness of rainfall on forage productivity. NDVI encapsulates tree cover, grass cover as well as moisture retention in the soil and thus, is more representative of variable forage production across landscapes. Trees improve soil moisture retention and thus positively promote grass production. This result demonstrated that temperature is not a direct determinant of forage availability in savannas. However, increasing temperature would likely make the rainfall less effective concerning forage production.

Disparate contractions in distributions of the three antelope species occurred throughout KNP post-1987, rather than manifesting only in the drier northern half or along specific rainfall or temperature gradients. The wide spread initial range shrinkages became evident during a sequence of years with below-average moisture when overall populations of these species declined.²⁷ For all three antelopes, the range reductions were coupled with the loss of herd units that had previously established during high rainfall years. The extremely severe drought of 1991/92 accentuated range contractions for all three species. The final extirpation of isolated herds of roan and tsessebe, as well as many herds, which had previously continuously occupied regions of KNP occurred during this 1991/92 period. Macandza et al.³⁵ reported that 15 sable antelope herds totalling over 200 animals roaming the Punda Maria section of KNP around 1987 had become reduced to a single herd of about 20 animals after 2003. In the Pretoriuskop section, Le Roux⁵³ reported that sable herd numbers changed little until the severe 1991/92 drought, after which many long-standing herds were no longer recorded. Numbers of around 450 sable antelope in 30 breeding herds recorded in this region around 1987 had declined to under 100 animals in no more than 7 herds by 2004.⁵⁴ Hence, for sable antelope, the range contraction was almost as severe in this wettest region of KNP as in the drier north.³⁵ All tsessebe herds plus the single roan herd found in the southern half of KNP also became extirpated. In the Greater Limpopo Transfrontier Conservation Area, north of KNP, Gandiwa et al.¹ reported comparably strong influences that rainfall has on larger herbivores populations, particularly during dry years. Ogutu et al.⁵⁵ reported similar changes of large herbivore populations as driven by influences of rainfall during dry periods for the Mara region in Kenya.

Pienaar³¹ showed sable antelope to be more widely distributed in west-central and far north-east regions of KNP around the 1960s whilst roan antelope occurred more widely in the western region of the northern half of the park. Tsessebe were recorded throughout much of the west-central region of KNP, as well as in western sections of the far north.³¹ Localities that had formerly supported herds no longer did so following persistently dry conditions. Ogutu & Owen-Smith²³ connected widespread declines among less common ungulate populations in KNP after 1986 to extremely little rainfall during dry season months. These authors noted that prevailing temperature conditions rose by about 0.4ºC around the time of the population declines. Persistently warmer conditions elevate plant respiration and hence lead to a more rapid loss of green foliage to the detriment of forage quality. Statistical support for models on NDVI support this position; the persistent high temperature would have reduced the effectiveness of rainfall since warmer conditions lead to more rapid evaporation of soil moisture.

This study has documented how adverse conditions, through reduced forage production/retention, both lead to contracted and fragmented distributions of three antelopes in a region at the southern fringe of their historic distributions. Range contractions were associated with local herd extirpations, but not shifts along rainfall or temperature gradients. Climate variation might affect these species not only through changing food resources, but also indirectly through ramifying interactions related to susceptibility to predation and competition linked to surface water access.^36,56 All of these mechanisms play out within a changing spatial template. Small antelope herds persisted as discrete remnants in their formerly wider distribution in places where conditions remained suitable. Globally, human dominance is generating widened climatic variation and opportunities for herbivore displacement outside conservation areas are constricted. Therefore, heterogeneity in habitat conditions becomes a key aspect in understanding responses of large mammals in savannas to climate change. Widely accepted assumptions about redistributions tracking suitable environmental gradients did not receive statistical support in KNP. The phenomena might apply for temperate zones where rainfall and subsequently forage availability are largely uniform in space.

Although numerous changes cannot be predicted with respect to extent or direction, changes are eminent under global warming⁵⁷ and should be included in conservation planning. Movements outside fenced parks are constricted; hence, species are likely to experience changes beyond their tolerance levels and could be in danger of extinction. All three antelope ranges expanded during higher rainfall periods, but expansions reversed during the moisture deficit periods. Therefore, for African savannas, contributions of spatial heterogeneity in habitat suitability remain important. For successful conservation, this study emphasises the need to shift focus from demographic mechanisms allied to life history features towards the more immediate consequences of changing environmental contexts through space and time on persistence.

Agricultural Research Council, South Africa.

We thank the Scientific Services Division of Kruger National Park for providing us with access to their aerial survey records, which enabled our analysis.

The authors declare that there is no conflict of interest regarding the publication of this article.

1. Gandiwa E, Heitkönig IMA, Eilers PHC, et al. Rainfall variability and its impact on large mammal populations in a complex of semi-arid African savanna protected areas. Tropical Ecology. 2016;57:163‒180.
2. Owen-Smith N. Demography of a large herbivore, the greater kudu Tragelaphus strepsiceros, in relation to rainfall. Journal of Animal Ecology. 1990;59(3):893‒913.
3. Coe MJ, Cumming DH, Phillipson J. Biomass and production of large African herbivores in relation to rainfall and primary production. Oecologia. 1976;22(4):341‒354.
4. Hanski I. Dynamics of regional distribution: the core and satellite species hypothesis. Oikos. 1982;38(2):210‒221.
5. Bock CE, Ricklefs RE. Range size and local abundance of some North American songbirds: A positive correlation. The American Naturalist. 1983;122(2):295‒299.
6. Brown JH. On the relationship between abundance and distribution of species. The American Naturalist. 1984;124:255‒279.
7. Lawton JH. Range, population abundance and conservation. Trends in Ecology and Evolution. 1993;8(11):409‒413.
8. Gaston KJ. Patterns in the geographic ranges of species. Biological Reviews. 1990;65(2):105‒129.
9. Gaston KJ. What is rarity? In: Kunin WE, Gaston KJ, editors. The biology of rarity: causes and consequences of rare-common differences. Chapman & Hall, London; 1997. p. 12‒30.
10. Gaston KJ, Quinn RM, Blackburn TM, et al. Species-range size distributions in Britain. Ecography, 1998;21:361‒370.
11. Gaston KJ, Curnutt JL. The dynamics of abundance-range size relationships. Oikos.1998;81(1):38‒44.
12. Woodroffe R, Groom R, Weldon J, et al. Hot dogs: High ambient temperatures impact reproductive success in a tropical carnivore. Journal of Animal Ecology. 2017;86(6):1329‒1338.
13. Cahill AE, Aiello-Lammens ME, Fisher-Reid MC, et al. How does climate change cause extinction? Proceedings of the Royal Society B-Biological Sciences. 2012;280:20121890.
14. Parmesan C, Ryrholm N, Stefannescu C, et al. Poleward shifts in geographical ranges of butterfly species associated with regional warming. Nature. 1999;399:579‒583.
15. Thomas CD, Lennon JJ. Birds extend their ranges northwards. Nature. 1999;399:213.
16. Walther G, Post E, Convey P, et al. Ecological response to recent climate change. Nature. 2002;416:398‒395.
17. Hickling RW, Roy BD, Hill JKW, et al. The distributions of a wide range of taxonomic groups are expanding polewards. Global Change Biology. 2006;12(3):450‒455.
18. Brander K, Blom G, Borges MF, et al. Changes in fish distribution in the eastern North Atlantic: Are we seeing a coherent response to changing temperature? ICES Marine Science Symposia. 2003;219:261‒270.
19. Mduma SAR, Sinclair ARE, Hilborn R. Food regulates the Serengeti wildebeest: A 40-year record. Journal of Animal Ecology. 1999;68(6):1101‒1122.
20. McNamara MJ, Houston IA. Starvation and predation as factors limiting population size. Ecology. 1987;68(5):1515‒1519.
21. Walker BH. Ecological consequences of atmospheric and climate change. Climatic Change. 1991;18(2-3):301‒316.
22. Chamaillé-Jammes S, Valeix M, Fritz H. Managing heterogeneity in elephant distribution: interactions between elephant population density and surface-water availability. Journal of Applied Ecology. 2007;44(3):625-633.
23. Cain III JW, Krausman PR, Rosenstock SS, et al. Mechanisms of Thermoregulation and Water Balance in Desert Ungulates. Wildlife Society Bulletin. 2006;34(3):570‒581.
24. Muposhi VK, Gandiwa E, Chemura A, et al. Habitat heterogeneity variably influences habitat selection by wild herbivores in a semi-arid tropical savanna ecosystem. PLoS ONE. 2016;11(9):e0163084.
25. Caughley G, Grice D, Barker R, et al. The edge of the range. Journal of Animal Ecology. 1988;57(3):771‒785.
26. Chirima JG. Habitat suitability assessments for sable antelope. Ph.D. thesis, University of the Witwatersrand, Johannesburg; 2009.
27. Ogutu JO, Owen-Smith N. ENSO, rainfall and temperature influences on extreme population declines among African savanna ungulates. Ecology Letters. 2003;6(5):412‒419.
28. Viljoen PC, Retief PF. The use of the Global Positioning System for real-time data collected during ecological aerial surveys in the Kruger National Park, South Africa. Koedoe. 1994;37(1):183‒189.
29. Owen-Smith N, Ogutu J. Rainfallinfluences on ungulate population dynamics. Surface water availability: implications for heterogeneity and ecosystem process. In: du Toit JT, Rogers KH, Biggs HC, editors. The Kruger experience: Ecology and management of savanna heterogeneity. Island Press, Washington; 2003. p. 310‒333.
30. Owen-Smith N, Mills MGL. Manifold interactive influences on the population dynamics of a multispecies ungulate assemblage. Ecological Monographs. 2006;76(1):73‒92.
31. Pienaar U, de V. The large mammals of the Kruger National Park - Their distribution and present-day status. Koedoe. 1963;6(1):1‒37.
32. Estes RD. The behaviour guide to African mammals, including hoofed mammals, carnivores, primates. University of California Press, Berkeley; 1991.
33. Harrington R, Owen-Smith N, Viljoen PC, et al. Establishing the causes of roan antelope decline in the Kruger National Park, South Africa. Biological Conservation. 1999;90(1):69‒78.
34. Owen-Smith N, Mills MGL. Predator–prey size relationships in African large-mammal food web. Journal of Animal Ecology. 2008;77(1):173‒183.
35. Macandza V, Owen-Smith N, Cain JW. Dynamic spatial partitioning and coexistence among tall grass grazers in an African savanna. Oikos. 2012;121(6):891‒898.
36. Chirima JG, Owen-Smith N, Erasmus BFN, et al. Distributional niche of relatively rare sable antelope in a South African savanna: habitat versus biotic relationships. Ecography. 2013;36(1):68–79.
37. Venter FJ, Scholes RJ, Eckhardt HC. The abiotic template and its associated vegetation pattern. In: du Toit JT, Rogers KH, Biggs HC, editors. The Kruger experience: Ecology and management of savanna heterogeneity. Island Press, Washington; 2003. pp. 82‒129.
38. Skinner JD, Chimimba CT. The mammals of the southern African subregion. 3rd edn. Cambridge University Press, Cambridge; 2005.
39. Estes RD, Estes RK. The biology and conservation of the giant sable antelope. Proceedings of the Academy of Natural Sciences Philadelphia. 1974;126:73‒104.
40. Grobler JH. Aspects of the biology, population ecology and behaviour of the sable in the Rhodes Matopos National Park, Rhodesia. Arnoldia (Rhodesia). 1974;7:1‒36.
41. Venter FJ. A classification of land for management planning in the Kruger National Park. Ph.D. thesis, University of South Africa, Pretoria; 1990.
42. Redfern JV, Viljoen PC, Kruger JM. et al. Biases in estimating population size from aerial census: a case study in the Kruger National Park, South Africa. South African Journal of Science. 2002;98:455‒461.
43. Getz WM, Fortmann-Roe S, Cross PC, et al. LoCoH: nonparametric kernel methods for constructing home ranges and utilization distributions. PLoS ONE. 2007;2(2):1‒11.
44. Chirima JG, Owen-Smith N. Comparison of kernel density and local convex hull methods for assessing distribution ranges of large mammalian herbivores. Transactions in GIS. 2016;21(2):359‒375.
45. Getz WM, Wilmers C. A local nearest-neighbor convex-hull construction of home ranges and utilization distributions. Ecography. 2004;27(4):498‒505.
46. Soberón J, Peterson AT. Interpretation of models of fundamental ecological niches and species’ distribution areas. Biodiversity Informatics.2005;2:1‒10.
47. Hirzel AH, Le Lay G. Habitat suitability modelling and the niche theory. Journal of Applied Ecology. 2008;45(5):1372‒1381.
48. McNemar Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika. 1947;12(2):153‒157.
49. Berenson ML, Koppel NB. Why McNemar’s procedure needs to be included in the Business Statistics Curriculum. Decision Sciences Journal of Innovative Education. 2005;3(1):125‒136.
50. Agresti A. An introduction to categorical data analysis. John Wiley NY; 1996.
51. Crawley MJ. The R Book. John Wiley; 2007.
52. Anderson DR, Burnham KP. Avoiding pitfalls when using information-theoretic methods. Journal of Wildlife Management. 2002;66(3):912‒918.
53. Le Roux E. Habitat and forage dependency of sable antelope (Hippotragus niger) in the Pretoriuskop region of the Kruger National Park. Masters dissertation, University of the Witwatersrand, Johannesburg; 2011.
54. Whyte IJ. Rare antelope in the Kruger National Park: Trends, current status, and options for future management. Internal Report, South African National Parks, Skukuza; 2006.
55. Ogutu JO, Owen‐Smith N, Piepho HP, et al. Continuing wildlife population declines and range contraction in the Mara region of Kenya during 1977-2009. Journal of Zoology. 2011;285(2):99‒109.
56. Owen-Smith N, Mason DR, Ogutu J. Correlates of survival rates for 10 African ungulate populations: density, rainfall and predation. Journal of Animal Ecology. 2005;74(4):774‒788.
57. Grover HD. Global climate change and planetary health. In Proceedings of the Fourth National Environmental Health Conference. San Antonio, Texas; 1990. p. 93‒108.