
Research Article Volume 3 Issue 1
Poisson area-biased lindley distribution and its applications on biological data
Shakila Bashir,
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Mujahid Rasul
Department of Statistics, Forman Christian College, Pakistan
Correspondence: Shakila Bashir, Assistant Professor, Department of Statistics, Forman Christian College (A Chartered University) Ferozepur Road Lahore (54600), Pakistan, Tel 92 (42) 9923 1581
Received: December 07, 2015 | Published: January 13, 2016
Citation: Bashir S, Rasul M. Poisson area-biased lindley distribution and its applications on biological data. Biom Biostat Int J. 2016;3(1):27-35. DOI: 10.15406/bbij.2016.03.00058
Download PDF
Abstract
The purpose of this paper is to introduce a discrete distribution named Poisson-area-biased Lindley distribution and its applications on biological data. Poisson area-biased Lindley distribution is introduced with some of its basic properties including moments, coefficient of skewness and kurtosis are discussed. The method of moments and maximum likelihood estimation of the parameters of Poisson area-biased Lindley distribution are investigated. It is found that the parameter estimated by method of moments is positively biased, consistent and asymptotically normal. Application of the model to some biological data sets is compared with Poisson distribution.
Keywords: PABLD, PD, PLD, area-biased, MOM, MLE; factorial moments
Introduction
Lindley1 introduced a single parameter distribution named as Lindley distribution with probability distribution function (pdf)
(1.1)
The pdf (1.1) is the mixture of exponential
and gamma
distributions. The cumulative distribution function (cdf) of the Lindley distribution is
(1.2)
The first two moments of the Lindley distribution are
Sankaran2 introduced the Lindley mixture of Poisson distribution named Poisson-Lindley distribution with the following pdf
(1.3)
The pdf (1.3) is applied to count data and arises from Poisson distribution when its parameter
follows a Lindley distribution. Ghitany & Al-Mutairi3 discussed various properties of the Lindley distribution. Ghitany & Al-Mutairi3 introduced size-biased Poisson Lindley distribution with applications. They considered the size biased form of the Poisson-Lindley distribution. Ghitany & Al-Mutairi4 discussed estimation methods for the discrete Poisson-Lindley distribution. Srivastava & Adhikari5 introduced a size-biased Poisson-Lindley distribution which is obtained by considering the size-biased form of the Poisson distribution with Lindley distribution without its size-biased form. Adhikari & Srivastava6 proposed a Poisson size-biased Lindley distribution which is obtained by computing Poisson distribution without its size-biased form with size-biased Lindley distribution. Shanker & Fesshaye7 discussed Poisson-Lindley distribution with several of its properties including factorial moments and parameter estimation. They applied the Poisson-Lindley distribution on ecology and genetics data sets and showed that it can be an important tool for modeling biological science data.
Rao8 introduced the distributions that are used in situations when the recorded observations do not have an equal probability of selection and do not have the original distribution. The distributions used to handle such situations are called weighted distributions. Suppose that the original distribution comes from a distribution with pdf
and the observations is recorded to a probability re-weighted by a weight function
then the weighted distribution is defined as
(1.4)
The weighted distribution with
is called size-biased/length-biased distributions and
is called area-biased distribution. Patil & Ord9 discussed size-biased sampling and related form-invariant weighted distributions. Patil & Rao10 discussed some models leading to weighted distributions and showed applications of weighted distributions in many real sampling problems. Mir & Ahmad11 introduced size-biased form of some discrete distributions with their applications.
In this paper we consider the Poisson area-biased Lindley distribution (PABLD) which is obtained by considering Poisson distribution without its area-biased form with area-biased Lindley distribution (ABLD).
Poisson area-biased lindley distribution
The Poisson area-biased Lindley distribution (PABLD) arises from the Poisson distribution with pdf
(2.1)
when its parameter
follows the area-biased Lindley distribution (ABLD) in (2.1) with pdf
(2.3)
So
After simplifying it the pdf of PABLD is obtained
(2.4)
Properties of the poisson-area-biased-lindley distribution
The factorial moments of the PABLD in (2.1)
(2.5)
For
in (2.5), the first four factorial moments of the PABLD are
,
,
,
(2.6)
Since the first four raw moments of the PABLD are
,
(2.7)
,
(2.8)
The mean moments of PABLD are
(2.9)
(2.10)
(2.11)
The coefficient of skewness and kurtosis of the PABLD are
(2.12)
(2.13)
For the PABLD, from (2.12) and (2.13) it can be seen that
as
, the model is negatively skewed and leptokurtic.
Some more properties of the PABLD are
(2.15)
The dispersion of the PABLD is defined to be
From equation (2.14) and Table 1, it can be observed that the PABLD is over-dispersed but as
then
and the PABLD is equi-dispersed. Therefore for large
the PABLD is equi-dispersed.
θ |
|
θ |
|
0.5 |
σ2 — 50.20408 |
19 |
σ2 — 0.012792 |
1 |
σ2 — 11.4375 |
20 |
σ2 — 0.011371 |
2 |
σ2 — 2.46 |
21 |
σ2 — 0.010169 |
3 |
σ2 — 0.972222 |
22 |
σ2 — 0.009144 |
4 |
σ2 — 0.497449 |
23 |
σ2 — 0.008263 |
5 |
σ2 — 0.294375 |
24 |
σ2 — 0.007502 |
6 |
σ2 — 0.191358 |
25 |
σ2 — 0.006839 |
7 |
σ2 — 0.132857 |
26 |
σ2 — 0.006258 |
8 |
σ2 — 0.096849 |
27 |
σ2 — 0.005748 |
9 |
σ2 — 0.073302 |
28 |
σ2 — 0.005296 |
10 |
σ2 — 0.05716 |
29 |
σ2 — 0.004894 |
11 |
σ2 — 0.045665 |
30 |
σ2 — 0.004536 |
12 |
σ2 — 0.037222 |
31 |
σ2 — 0.004215 |
13 |
σ2 — 0.030857 |
32 |
σ2 — 0.003927 |
14 |
σ2 — 0.025952 |
50 |
σ2 — 0.00147 |
15 |
σ2 — 0.022099 |
100 |
σ2 — 0.000335 |
16 |
σ2 — 0.019023 |
500 |
σ2 — 1.23E-05 |
17 |
σ2 — 0.016531 |
1000 |
σ2 — 3.04E-06 |
18 |
σ2 — 0.014487 |
∞ |
σ2 |
Table 1 The dispersion of PABLD for different values of θ
Method of moments
If
be the random sample from PABLD with pdf (2.4), the method of moments (MOM) estimate
of the parameter
is given by
(3.1)
Theorem 1: The MOM estimator
of
is positively biased.
Proof: Let
, where
So,
(3.2)
Then
is strictly convex. By using the Jensen’s inequality we have
Since
, therefore
Theorem 2: The MOM estimator
of
is consistent and asymptotically normal:
Where
(3.3)
Proof: -
Consistency: Since
then
And
is a continuous function at
, then
i-e.
Asymptotic normality: as
then by using the central limit theorem we have
is a differentiable function and
then by using the delta-method we have
Finally we have
and
(3.4)
The theorem 2 follow the asymptotic
confidence interval for
is
(3.5)
Maximum likelihood estimation
Let
be the random sample on size n from PABLD with pdf (2.4), the maximum likelihood estimate (MLE)
of the parameter
is the solution of the non-linear equation:
(4.1)
Applications
In this section the PABLD is applied to some biological data sets and compared with PD.
- Guire, et al.12 gave data on European corn borers per plant with 0, 1, 2, 3 and 4 and counts 83, 36, 14, 2, and 1.
Form Table 2, it can be seen that the PABLD gives much closer fit than the PD and PLD to the data set of number of bores per plant . Thus PABLD provides a better alternative to PD and PLD for modeling count data sets.
- Beall13 gave the distribution of Pyrausta nublilalis in 1937, no of insects 0, 1, 2, 3, 4 and 5 with counts 33, 12, 6, 3, 1 and 1.
Form Table 3, it can be seen that the PABLD gives better fit than the PD to the data set of number of insects. Thus PABLD provides a better alternative to PD for modeling count data sets.
- Juday14 and Thomas 15 gave data on macroscopic fresh-water fauna in dredge samples from the bottom of Weber Lake.
Form Table 4 it can be seen that the PABLD gives better fit than PD and PLD to the animal distribution of microcalanus nauplii. Thus PABLD provides a better alternative to PD and PLD for modeling count data sets.
- Archibald16 gave data on plant populations. The distribution of representing salicornia stricta.
Form Table 5, it can be seen that the PABLD gives better fit than the PD and PLD. Thus PABLD provides a better alternative to PD and PLD for modeling count data sets.
- Archibald16-18 gave data on plant populations. The distribution of representing Plantago maritime.
Number of Bores Per Plant X |
Observed Frequency (Oi) |
Expected Frequency (Ei) |
Poisson Distribution |
Poisson-Lindley Distribution |
Poisson- Area-Biased Lindley Distribution |
0 |
83 |
78.9 |
87.2 |
82.4 |
1 |
36 |
42.9 |
31.8 |
38.1 |
2 |
14 |
11.7 |
11.2 |
11.7 |
3 |
2 |
2.01 |
3.8 |
2 |
4 |
1 |
0.4 |
2 |
0.67 |
Total |
136 |
136 |
136 |
135.87 |
Estimation of Parameters |
|
|
|
|
|
|
1.885 |
0.757 |
0.312 |
d.f |
|
1 |
1 |
1 |
p-value |
|
0.1698 |
0.3843 |
0.576455 |
Table 2 Chi-square goodness of fit test for PD, PLD and PABLD to European corn-borer data.
Number of Insects x |
Observed Frequency (Oi) |
Expected Frequency (Ei) |
Poisson Distribution |
Poisson Lindley Distribution |
Poisson Area-Biased Lindley Distribution |
0 |
33 |
26.45 |
31.48 |
33.18 |
1 |
12 |
19.84 |
14.16 |
15.98 |
2 |
6 |
7.44 |
6.09 |
5.09 |
3 |
3 |
1.86 |
2.5 |
1.34 |
4 |
1 |
0.35 |
1.04 |
0.32 |
5 |
1 |
0.05 |
0.42 |
0.07 |
Total |
56 |
55.99 |
55.73 |
55.98 |
Estimation of Parameters |
|
|
|
|
|
|
4.89 |
0.484 |
3.56 |
d.f |
|
1 |
1 |
1 |
p-value |
|
0.026977 |
0.00001 |
0.059131 |
Table 3 Chi-square goodness of fit test for PD, PLD and PABLD to distribution of Pyrausta nublilalis in 1937
Individuals Per Unit |
Microcalanus |
Observed Frequency (Oi) |
Expected Frequency (Ei) |
Poisson Distribution |
Poisson Lindley Distribution |
Poisson Area-Biased Lindley Distribution |
0 |
0 |
0.01 |
7.156 |
1.294 |
1 |
2 |
0.098 |
8.743 |
3.402 |
2 |
4 |
0.468 |
9.632 |
5.76 |
3 |
3 |
1.498 |
10.009 |
7.928 |
4 |
5 |
3.595 |
10.014 |
9.643 |
5 |
8 |
6.903 |
9.757 |
10.791 |
6 |
16 |
11.045 |
9.324 |
11.37 |
7 |
13 |
15.147 |
8.777 |
11.446 |
8 |
12 |
18.177 |
8.164 |
11.116 |
9 |
13 |
19.388 |
7.521 |
10.487 |
10 |
15 |
18.613 |
6.873 |
9.66 |
11 |
15 |
16.244 |
6.239 |
8.721 |
12 |
9 |
12.995 |
5.631 |
7.739 |
13 |
9 |
9.596 |
5.057 |
6.767 |
14 |
7 |
6.58 |
4.522 |
5.842 |
15 |
4 |
4.211 |
4.028 |
4.986 |
16 |
4 |
2.527 |
3.575 |
4.213 |
17 |
6 |
1.427 |
3.164 |
3.528 |
18 |
2 |
0.761 |
2.793 |
2.931 |
19 |
0 |
0.385 |
2.459 |
2.417 |
20 |
2 |
0.185 |
2.16 |
1.981 |
21 |
1 |
0.084 |
1.894 |
1.613 |
22 |
0 |
0.037 |
1.658 |
1.306 |
Total |
150 |
149.97 |
149.7 |
150 |
Estimation of Parameters |
|
|
|
|
|
|
30.39206 |
62.992 |
20.02153 |
d.f |
|
10 |
13 |
12 |
p-value |
|
0.000739 |
0.00001 |
0.06669 |
Table 4 Chi-square goodness of fit test for PD, PLD and PABLD to animal distribution of microcalanus nauplii
Plants Per Quadrant |
Salicornia |
Observed Frequency |
Expected Frequency (Ei) |
(Oi) |
Poisson Distribution |
Poisson Lindley Distribution |
Poisson Area-Biased Lindley Distribution |
0 |
4 |
0.127 |
7.874 |
2.277 |
1 |
3 |
0.843 |
8.939 |
5.267 |
2 |
8 |
2.804 |
9.199 |
7.861 |
3 |
13 |
6.216 |
8.947 |
9.553 |
4 |
11 |
10.333 |
8.389 |
10.265 |
5 |
9 |
13.743 |
7.665 |
10.156 |
6 |
8 |
15.232 |
6.871 |
9.465 |
7 |
10 |
14.471 |
6.069 |
8.43 |
8 |
3 |
12.029 |
5.299 |
7.245 |
9 |
3 |
8.888 |
4.582 |
6.05 |
10 |
8 |
5.91 |
3.931 |
4.934 |
11 |
3 |
3.573 |
3.35 |
3.943 |
12 |
4 |
1.98 |
2.839 |
3.099 |
13 |
4 |
1.013 |
2.394 |
2.399 |
14 |
0 |
0.481 |
2.01 |
1.834 |
15 |
3 |
0.213 |
1.681 |
1.387 |
16 |
0 |
0.089 |
1.402 |
1.038 |
17 |
0 |
0.035 |
1.165 |
0.77 |
18 |
1 |
0.013 |
0.966 |
0.566 |
19 |
0 |
0.004 |
0.799 |
0.414 |
20 |
3 |
0.001 |
0.659 |
0.3 |
Total |
98 |
97.99 |
98 |
97.25275 |
Estimation of Parameters |
|
|
|
|
|
|
65.55225 |
13.01986 |
7.381047 |
d.f |
|
7 |
8 |
8 |
p-value |
|
0.00001 |
0.111198 |
0.496138 |
Table 5 Chi-square goodness of fit test for PD, PLD and PABLD to distribution of quadrant, representing salicornia stricta
From Table 6 it is concluded that the PABLD gives better fit than the PD and almost equally good fit as PLD distribution to the distribution of Plantago maritime. Therefore the PABLD is better alternative to PD and PLD to model discrete data sets.
Plants per Quadrant |
Plantago |
Observed Frequency |
Expected Frequency (Ei) |
Poisson Distribution |
Poisson Lindley Distribution |
Poisson Area-Biased Lindley Distribution |
0 |
12 |
0.6409 |
11.471 |
4.273 |
1 |
8 |
3.2367 |
12.166 |
8.868 |
2 |
9 |
8.1727 |
11.749 |
11.897 |
3 |
13 |
13.7574 |
10.746 |
13.009 |
4 |
6 |
17.3687 |
9.484 |
12.59 |
5 |
8 |
17.5424 |
8.163 |
11.223 |
6 |
11 |
14.7648 |
6.895 |
9.428 |
7 |
7 |
10.652 |
5.741 |
7.571 |
8 |
8 |
6.7239 |
4.725 |
5.868 |
9 |
7 |
3.7729 |
3.853 |
4.42 |
10 |
3 |
1.9053 |
3.117 |
3.251 |
11 |
4 |
0.8747 |
2.505 |
2.344 |
12 |
1 |
0.3681 |
2.002 |
1.662 |
13 |
1 |
0.143 |
1.592 |
1.161 |
14 |
0 |
0.0516 |
1.261 |
0.801 |
15 |
0 |
0.0174 |
0.995 |
0.547 |
16 |
1 |
0.0055 |
0.782 |
0.369 |
17 |
0 |
0.0016 |
0.613 |
0.247 |
18 |
0 |
0.0005 |
0.48 |
0.164 |
19 |
1 |
0.0001 |
0.374 |
0.108 |
20 |
0 |
0.00003 |
0.291 |
0.071 |
Total |
100 |
99.999 |
99.89 |
99.8709 |
Estimation of Parameters |
|
|
|
|
|
|
55.48343 |
7.084 |
10.2781 |
d.f |
|
6 |
7 |
7 |
p-value |
|
0.00001 |
0.420187 |
0.173359 |
Table 6 Chi-square goodness of fit test for PD, PLD and PABLD to distribution of quadrant, representing Plantago maritima
Note: The highlighted expected frequencies from Table 2-6 are the pooled frequencies that are less than 5, so the degrees of freedom are calculated according to them.
From Table 2-7, it is observed that the PABLD gives better fit than PD and PLD to the some biological count data sets. PD is a discrete distribution with parameter
. Lindley distribution is a continuous life time distribution and PLD is the mixture of Poisson and Lindley distributions with parameter
. The proposed model named PABLD is obtained by the mixture of the Poisson distribution and the area biased form of the Lindley distribution. The area biased distribution is a type of the weighted distribution with weight
, due to mixture of PD and LD with this weight, the proposed model is showing applications better than PD and PLD to biological data sets. Mostly the applications of the weighted distributions to the data relating biology can be found in Patil & Rao [10].
f. Interval Estimation: By using equation (3.5) the parameter
of PABLD is estimated by the interval estimation for the Biological data sets. The estimated interval for
of PABLD by the interval estimation is closer to the estimated value by MOM.
Table |
Data Sets |
95 % C. I |
II |
Number of bores per plant |
(5.989827, 6.249026) |
III |
Number of insects |
(5.562813, 6.155574) |
IV |
Microcalanus |
(0.39898, 0.40902) |
V |
Salicornia |
(0.568854, 0.591146) |
VI |
Plantago |
(0.738042, 0.766708) |
Table 7 The asymptotic 95% confidence intervals (C.I) for θ of PABLD
Conclusion
The Poisson area-biased Lindley distribution (PABLD) is discrete distribution that is obtained by mixture of the Poisson distribution and area-biased Lindley distribution. Some important properties of the PABLD are derived. From Figure 1 it can be seen that the PABLD is positively skewed moreover it can be seen that as
,
and the PABLD is negatively skewed and leptokurtic. Furthermore it is found that the PABLD is over-dispersed but as
the PABLD is equi-dispersed. The parameter of the PABLD is estimated by the method of moments (MOM) and it is proved that the
of
is positively biased, consistent and asymptotically normal. In section 4, the proposed model PABLD is applied to some biological data sets and compared with PD and PLD. It is observed that the PABLD gives better approach to the given data sets. Therefore it is concluded that PABLD is a better alternative to PD and PLD and it has useful applications in real life biological data sets. The asymptotic
confidence interval (C.I) for
of PABLD is also found on these data sets and it is observed that the estimated interval for
of PABLD by the interval estimation is closer to the estimated value obtained by MOM.
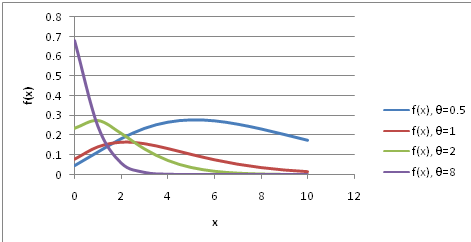
Figure 1 Plots of the pdf of PABLD for θ = 0.5, θ = 1, θ = 2, θ = 8.
Acknowledgments
Conflicts of interest
Author declares that there are no conflicts of interest.
References
- Lindley DV. Fiducial distributions and Bayes’ theorem. Journal of the Royal Statistical Society Series. 1958;20(1):102–107.
- Sankaran M. The discrete Poisson-Lindley distribution. Biometrics. 1970;26(1):145–149.
- Ghitany ME, Al-Mutairi DK. Size-biased Poisson-Lindley distribution and its application. International Journal of Statistics LXVI N. 2008;3:299–311.
- Ghitany ME, Al-Mutairi DK. Estimation methods for the discrete Poisson-Lindley distribution. Journal Statistical Computation and Simulation. 2009;79(1):1–9.
- Srivastava RS, Adhikari TR. A size-biased Poisson-Lindley distribution. International Journal of Scientific and Research Publications. 2013;4(1):1–6.
- Srivastava RS, Adhikari TR. Poisson-size-biased Lindley distribution. International Journal of Scientific and Research Publications. 2014;4(1):1–6.
- Shanker R, Fesshaye H. Biometrics and Biostatistics International Journal. 2015;2(4):1–5.
- Rao CR. On discrete distributions arising out of ascertainment. In: Patil GP, editors; Classical and Contagious Discrete Distributions, Pergamon. Press and Statistical Publishing Society, Calcutta, India. 1965;320–332.
- Patil GP, Ord JK. On size-biased sampling and related form- invariant weighted distributions. Sankhya. 1976;38(1):48–61.
- Patil GP, Rao CR. Weighted distributions and size-biased sampling with applications to wildlife populations and human families. Biometrics. 1978;34:179–189.
- Mir KA, Ahmad M. Size-biased distributions and their applications. Pak J Statistics. 2009;25(3):283–294.
- Mc Guire JU, Brindley TA, Bancroft TA. The distribution of European corn-borer larvae pyrausta in field corn. Biometrics. 1957;13(1):65–78.
- Beall G. The fit and significance of contagious distributions when applied to observations on larval insects. Ecology. 1940;21(4):460–474.
- Juday C. Data on the macroscopic fresh-water fauna in dredge samples from the bottom of Weber Lake. 1942.
- Thomas M. A generalization of Poisson’s binomial limit for use in ecology. Biometrika. 1949;36(2):18–25.
- Archibald EEA. Plant populations. I. A new application of Neyman’s contagious distribution. Ann Bot. 1948;12:221–235.
- Bliss CI, Fisher RA. Fitting the negative binomial distribution to Biological data. Biometrics. 1953;9(2):176–200.
- Ghitany ME, Atieh B, Nadarajah S. Lindley distribution and its applications. Mathematics and Computers in Simulation. 2008;78(4):493–506.

©2016 Bashir, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


