In this study, water management allocated for agricultural productions was analyzed using stochastic dynamic programming. The technical coefficients used in the study referred to the agricultural years, 2013-2014. They were obtained through the use of simple random sampling of 250 farmers in the region for crops wheat, barley, melon, watermelon, and ruby grapes under the scenarios of drought and wet, required in the most sensitive growth stages. Production function and profit function were obtained from the yield-water-product function of crops using Eviews software. Expected net profit of the system and optimal allocation of water were also calculated based on the GAMS economic analysis software. The results revealed that 0.47 % of the time and that 0.14% had experienced drought (low) and wet (High) years. In the best case, i.e. with high current levels, respectively at, 58, 67, 54, and 48% of water requirements for these crops and, in the worst case (with low current levels), 47, 35, 49, 53 and 48% of the water requirements provided during the most sensitive growth stages. Moreover, the results showed that the cultivation of the ruby grape was the best product with the highest expected profit in water and drought conditions.

Keywords: Expected value, Agricultural Production, Stochastic dynamic programming

From three perspectives, water plays a key role in sustainable development. First, it is consumed as a final product. Second, water is an important input element in many businesses. Third, it has a key role in biological organisms on Earth.¹ According to the latest estimates by UNESCO of the water cycle on Earth, it can be inferred that the average annual rainfall in Iran was 251 mm, having a significant difference with the average rainfall of each continent.² It could be compared with rainfall in semi-arid and desert-like countries of some continents.³ The average rainfall in all lands and Asia was 831 and 732 mm, respectively.⁴ In Iran, the average annual rainfall was 413 billion m³; however, the area of Iran is 1.1 % of all lands and 3.35% of the land area of Asia. Iran’s rainfall volume comprises just 0.37% of all rainfall from the earth’s lands and 1.29% of rainfall volume in Asia. Also, the average annual evaporation in Iran is estimated at about 70- 71% of annual rainfall. In this regard, just Africa and Australia, with 70% and 80% evaporation under undesirable rainfall conditions, respectively, are lower than Iran.⁵ The Hirmand basin is located in the province of Sistan and Baluchistan. In all climate categories, the Sistan region had a hot and dry climate. Based on different calculation methods, its average annual temperature was 21 °C, its annual rainfall was 61.4 mm, its relative humidity was 38%, and its potential evapotranspiration was 4196 mm.⁶ Of the total cultivated lands of the country, an area of 12 million hectares is located in Sistan and Baluchistan out of which 52.4% is located in the Sistan region.⁷ The purpose of this study was to estimate the economic allocation model of the Hirmand River Basin water resources in crop and garden productions using stochastic dynamic programming.

The yield-water-product function was used to estimate crop and garden production functions.⁸ Under each irrigation condition, crops and garden had their unique water-product functions estimated using regression methods (Dhehibi et al., 2014). This function expressed the relationship between the actual yield and the effective irrigation, so the second-degree polynomial function for estimating the crop- water function recommended by was as follows (1):

$\raisebox{1ex}{$Y_a$}\!\left/ \!\raisebox{-1ex}{$Y_m$}\right.=f\left(w\right)=a_0+a_{{}_1}w+a_{{}_2}{w}^2$ (1)

Where is the actual crop yield (tons / ha), is the maximum potential yield (t / ha),  is the ratio of total available water to the maximum potential seasonal evaporation in the crop, i.e. the ratio of actual evapotranspiration to the potential evapotranspiration. Based on the water- crop yield, the total profit yield of irrigation water is expressed as follows:⁹ 

${\beta }_j^{\sim }={{\displaystyle \sum }}^{\text{}}PC{P}_{cp}.Y{a}_{cp.}A{f}_{cp} -{{\displaystyle \sum }}^{\text{}}V{c}_{cp}.A{f}_{cp}$ (2)

Whereis the crop price, andis the variable costs of crop production. The target function can be written as;(3)

$max{\beta }_j^{\sim }$ $s.t: {\displaystyle \sum }_{cp}A{f}_{cp}\le A$ $A{f}_{cp}^i\le A{f}_{cp}\le A{f}_{cp}^u$ ${\displaystyle \sum }_{CP}E{I}_{cp}.A{f}_{cp}\le Q$

Where is the total area under cultivation (ha) andandare respectively the maximum and minimum levels of cultivated areas (ha), is the rate of effective irrigation required during the growing season (m³ / ha) and Q is the total amount of effective irrigation available in the region. Since the system manager always faces issues regarding water allocation between competing agricultural consumers (including various scenarios) and due to the fact that water supply tends be random in the future, the demand for water will also be estimated based on the needs of different scenarios and a logical period will be considered for all data.¹⁰ In cases where the agricultural sector is informed that it has little water available, it will change its activities so that it would need less water. When there is uncertainty, the manager is supposed to create a plan in which, despite allocation of water efficiency, the system benefits increase, and in turn, the system risk reduces.¹¹ Hence, the random variable of water supply with P_tk (probability scenario k in time period t) was used to design a set of scenarios with branching structure. This model can be formulated as follows (4):

$\max f^{+}={\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{t=1}^{T}N{B}_{it}^{+}(W_{it}^{-}+\Delta W_{it}{y}_{it})-{\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{j=1}^n{\displaystyle \sum }_{k=1}^{r}P{C}_{tk}^{+}{D}_{itk}{}^{+})$ (4)

$s.t q_{th}^{-} \ge {\displaystyle \sum }_{i=1}^m(W_{it}^{-}+\Delta W_{it}{y}_{itop}-D_{itk}{}^{+})$ $\forall h,k=1,2\dots k ,t=1,2,\dots T$ $W\frac{\pm }{imax}\ge W_i{t}^{-}+\Delta W_{{}_{i}t}{y}_{{}_{2}t}\ge D_i{t}^{+}>0?i,t,k$

$D_{itk}{}^{\pm }\ge D_{itkOP}{}^{-} \text{و} t=1,2,\dots T$

Where F is the net system profit of the planning horizon is the net income of i^th crop per allocated water unit, water promised for the product i,  is the farmer’s losses per unit of water promised, but not delivered in period t, D_itk is water scarcity for the crop i under scenario k in period t (in other words, some of  was not delivered at q^th), q^th is random variable of water supply in period t, is the amount of water allocated for i^th consumer at time t, P_tk is frequency probability of scenario k in period t, k are total number of scenarios and t is the most sensitive growth stage, i is the type of crop (i = 1 wheat, i = 2 barley, i =3 melon, i = 4 watermelon, and i = 5, ruby ​​grape). In this equation, is a decision variable used to define the optimal range. When reaches its highest level, . If the required water is delivered to the sectors, the system profit will reach its peak level. In case of losses, the reverse is true, too. When  and the promised rate of water is delivered, the system profit will decrease dramatically, but if the promised water is supplied, it would have the least amount of loss for the system.The valueis obtained from the model 4). Using the solutions of the models (4), the following equations are obtained: (5)

 As a result, the optimal water allocation for the planned period is calculated as follows:¹² 

Research data

 Technical factors used in the study corresponded to the farming years 2013-2014. Research was conducted through simple random sampling of 250 regional farmers. Moreover, in order to calculate the possibility of water flow rate (low or High) based on rainfall data gathered from 3 decades ago to the present and using the standardized precipitation index, the percentages of dry, wet, and normal years were obtained. These percentages were used to determine the frequency possibility of low and medium water flows. The Standard Precipitation Index is defined as follows (7):

$SPI=\left(P_i–S\right)/P$

Where SPI is the standard precipitation index, Pi is desired annual rainfall, P is long-term average rainfall, and S is the standard deviation of long-term rainfall. If the index is greater and/or less than 1, it means that wet and drought conditions exist, respectively. Rates between 1 and -1 represent a year with normal and average rainfall (Table 1). The results showed that the number of years with an amount of precipitation less than the average (i.e. drought) is higher than the number of years that are higher than the average amount of precipitation (wet years). Over the past 30 years, 0.14 % of cases had wet states (high) and 0.47 % had drought cases.^13,14

The rate of target allocation of water for agricultural crops was calculated by the gross irrigation requirement. Likewise, its maximum and minimum rates were also considered in terms of the highest and lowest water use efficiency in the region. The variable of maximum allocation of water to different crops was calculated based on the most unfavorable efficiency of the irrigation area. Table 2 summarizes this information. Allocation of water under the drought scenario for wheat, barley, melon, and watermelon are presented in Table 3. In addition Target water demand and allocated water in drought scenario are presented in Figure 1. The solution of the target functionrepresented two final expected values of net profit in the irrigation models for wheat, barley, melon, and watermelon under drought scenarios and during the planning horizon which varies between the maximum and minimum levels. If the manager will be conservative and he will promise the provision of less water to the farmers. If the promised water to the farmer is not delivered, he will choose the loss incurred from a lower harvest. Since this happens just under drought conditions, it is wise for the manager to behave moderately. Moreover, the results of the optimal allocation of water in drought conditions showed that using ruby ​​grapes would lead to the lowest expected value. Based on the information mentioned in Tables 1 and Tables 2 the optimal allocation of water under the normal scenario for wheat, barley, melon, and watermelon are presented in Table 4. The solution of the target functionwas positive at the final value of the expected net profit of the crop under a normal scenario. If, the manager is supposed to act optimistically and promise high levels of water needed. The results of optimal allocation of water in wet conditions showed that cultivation of ruby ​​grapes could provide the highest expected profits.¹⁵

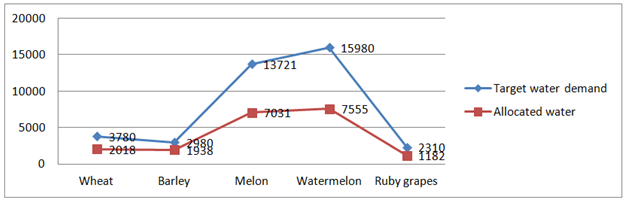
Figure 1 Target water demand and allocated water in drought scenario.

Reference: researcher’s calculations

Figure 2 Target water demand and allocated water in wet scenario.

In this study, economic allocation of water allocated to agricultural sector was analyzed using randomly dynamic programming. Technical factors used in the study referenced the farming years 2013-2014. It was conducted through a simple random sampling of 250 farmers in the region for crops wheat, barley, melon, watermelon, and ruby grapes. By inserting the amounts of water scarcity and water allocation in the target function, the profit earned from economic allocation of water was obtained. The results revealed that 0.47% experienced drought (low) and 0.39% had a wet (average) year. The results also showed that the rates of final water allocation in drought conditions for wheat, barley, melon, watermelon and ruby grapes were, respectively 2018, 1938, 7555,7031,1182 m³and in normal conditions, they were 2025, 1942, 7046, 7559, and 1189m³. The results also showed that ruby grapes were the ​​best crop with the highest expected profit in drought and wet conditions. . In general, whenever the expected net income value of some crops is positive, the managers will act optimistically and the high levels of water required are promised to the farmers. In turn, they would prefer to be more conservative and would promise the least amount of water provided to the farmers. Hence, if the promised water to the farmer is not wasted, he will choose the loss incurred from a lesser harvest.

It has been suggested to choose the type of crops based on the irrigated conditions. Moreover, if the farmers have enough freedom to choose and use different variables, the model can provide practical solutions in terms of establishing the amount of profit in farmers’ mental calculations. Since in this study, the expected profit was obtained in drought and normal scenarios under the most sensitive water requirement conditions, it is wise to consider several measures so that sustainable water could be provided to the farmers to grow crops on time and earn the minimum rate of household income. It would reduce the migration of Sistani villagers to cities and neighboring provinces. It is significant to note that if the east of the country becomes haunted it will endanger the security of the area and the whole country.

None.

The author declares there is no conflicts of interest.

1. Divakar L. Optimal allocation of bulk water supplies to competing use sectors based on economic. Journal of Hydrology. 2010;22–35.
2. Kessler J, M Van Drop. Ructural adjustment and the environment: The need for an analytical methodology. Ecological Economics. 2011;27:267–281.
3. Lynch H, Campbell Grant E, Muneepeerakul R, et a. How restructuring river connectivity changes freshwater fish biodiversity and biogeography. Water resource research. 2011;45(5):112–117.
4. Thompson D, R Powell. Exceptional circumstances provisions in Asia, is there too much emphasis on drought? Agricultural Systems. 2012;57:469-488.
5. Mihankhah M. Management and optimum utilization of water resources by using dynamic programming. Economic and agricultural development. 2012;4:244–251.
6. Ebrahimzade E, G Lashkaripoor. Drought crisis in Sistan and adjust its strategies. A quarterly journal of Rural Dvelopment Studies. 2013;2:73–91.
7. Sharaki J, M Mohamadghasemi. Economic allocation of water resources in the region of Sistan using dynamic optimization. Paper presented at the Intrnational Conference on sustainable development, stratege and challengs, Tbriz-Iran. 2014.
8. Tu MY J, NS H, Y WWG. Optimization of reservoir management and operation with hedging rules .Water Resour Plan Manag-ASCE. 2011;129:86–97.
9. Dorfman R. An Economic Interpret ion of optimal control. American Economic Review. 2012;25:25–34.
10. Zeng X, HU T, Gx Li. Wter transfer triggering mechanism for multi- riservoir operation in inter- basin wate transfer- supply project. Water resour manage. 2014;28:1293–1308.
11. Homauonifar R. Latian Dam water allocation among crops in conditions of uncertainty. Economic and agricultural development. 2011;24:267–259.
12. Cooper WW, Seiford LM, Zhu J. Handbook on Data Envelopment Analysis. 2nd ed. Springer Science+ Business Media, LLC. 2011. 512 p.
13. Dhehibi B, Alimari A, Haddad N, et al. Technical Efficiency and Its Determinats in Food Croop Production: A Case study of Farms in West Bank, Palestine. J Agr sci Tech. 2014;16:717-730.
14. Emrouznejad A, Tavana M. Performance Mesuerment with Fuzzy Data Envelopment Analysis. Studies in Fuzziness and Soft Compoting. Springer- Verlag Berlin, Heidelberg. 2014. 293 p.
15. Ghaffour N, Missimer T, Amy G. Technical review and evaluation of the economics of water desalination: current and future challenges for better water supply sustainability Water Resour Manag. 2013.